Abstract
We investigate the boundary lubrication in weakly adhered molecularly thin films deposited between a sphere and a plane, below the sliding threshold. The shear contact stiffness and interfacial dissipation at the micrometer scale are determined with a high-frequency quartz oscillator.
Two distinct behaviors are found as a function of the shear oscillation: a linear viscoelastic response at low amplitude and a nonlinear frictional microslip at high amplitude. A friction model is proposed to analyze the data, which allows evaluating the shear strength, the friction coefficient, and the interfacial viscosity at different solid interfaces under low load.
我们研究了沉积在球面和平面之间、低于滑动阈值的弱粘附分子薄膜的边界润滑。我们使用高频石英振荡器测定了微米尺度的剪切接触刚度和界面耗散。
我们发现了两种截然不同的行为都是剪切振动的函数:低振幅时的线性粘弹响应和高振幅时的非线性摩擦微滑动。提出了一个摩擦模型来分析数据,该模型可以评估低负荷下不同固体界面的剪切强度、摩擦系数和界面粘度。
Introduction
Thin films deposited on solid surfaces are extensively used to tailor a broad range of properties such as optical transmission, electronic transport, adhe- sion, or lubrication. As the thickness of the thin film $h$ is decreased down to a characteristic length scale relevant for a given physical mechanism, some confinement effects take place. Furthermore, the nonlinear mechanical behavior may come into play due to large shear strains $\varepsilon_{T}$~$U_{T}/h$ at a given shear amplitude $U_{T}$. Highlighting the mechanisms responsible for the nonlinear properties of thin films is essential for understanding phenomena such as dewetting and solid friction.
沉积在固体表面的薄膜被广泛用于定制各种特性,如光学传输、电子传输、粘附或润滑。当薄膜的厚度 $h$ 下降到与特定物理机制相关的特征长度尺度时,就会产生一些限制效应。此外,在给定的剪切振幅 $U_{T}$ 下,由于剪切应变 $\varepsilon_{T}$~$U_{T}/h$ 较大,非线性机械行为可能会发挥作用。突出薄膜非线性特性的机理对于理解露湿和固体摩擦等现象至关重要。
Indeed, thin films highly confined between flat contacting solid surfaces under shear ($h$
$1\text{ nm}$) control the friction dynamics of the interface. In such a boundary lubrication regime, the static friction threshold $F_{T}$ is commonly described by the classical Amontons-Coulomb laws, $F_{T} = \mu N$ with $N$ the normal load and $\mu$ the coefficient of friction. Following Tabor, the threshold can be alternatively expressed as $F_{T} = \sigma_{S}\Sigma_{r}$ where $\Sigma_{r}$ is the real contact area proportional to $N$ and $\sigma_{s}$ is the interfacial shear strength. Baumberger and Caroli have recently shown that $\sigma_{s}$ corresponds to the yield stress of the interfacial layer (junction) consisting of a molecularly disordered medium with $h$$1\text{ nm}$.
事实上,在剪切力($h$$1\text{ nm}$)作用下,高度约束于接触固体表面之间的薄膜控制着界面的摩擦动力学。在这种边界润滑机制中,静摩擦阈值 $F_{T}$ 通常由经典的 Amontons-Coulomb 定律来描述,即 $F_{T} = \mu N$ ,其中 $N$ 为法向载荷,$\mu$ 为摩擦系数。按照 Tabor 的方法,阈值也可以表示为 $F_{T} = \sigma_{S}\Sigma_{r}$ 其中 $\Sigma_{r}$ 是与 $N$ 成比例的实际接触面积,$\sigma_{s}$ 是界面剪切强度。Baumberger 和 Caroli 最近证明,$\sigma_{s}$ 相当于由分子无序介质组成的界面层(交界处)的屈服应力,该介质的厚度为 $h$$1\text{nm}$。
At low shear level the interfacial layer is pinned and responds to shear elastically; beyond the threshold it flows plastically due to the structural rearrangements at the nanometric scales within the junction. On the other hand, it has been shown that the adhesion may play a crucial role in the static threshold. Under low normal load, the modified Coulomb law reads $F_{T} = F_{0} + \mu N$ where $F_{0}$ is the shear threshold under zero load. However, the physical mechanisms that precede the threshold $F_{T}$ and the interplay between friction and adhesion remain poorly understood due to the lack of experimental data.
在低剪切力水平,界面层被钉住并对剪切力做出弹性响应;超过阈值后,由于交界处纳米尺度的结构重排,界面层会发生弹性流动。另一方面,研究表明,粘附力可能对静态阈值起着至关重要的作用。在低正常负载下,修正的库仑定律为 $F_{T} = F_{0} + \mu N$,其中 $F_{0}$ 是零负载下的剪切阈值。然而,由于缺乏实验数据,人们对阈值 $F_{T}$ 出现之前的物理机制以及摩擦力和附着力之间的相互作用仍然知之甚少。
Alternatively, the frictional dynamics can be studied with the sphere-plane geometry. For a loaded nonadhesive contact between a smooth sphere and a plane surface, Mindlin derived a relationship between the shear displacement and the tangential force. When the amplitude of the shear displacement increases, a micro-slip annulus grows from the edge of the contact area towards the center, until the macroscopic sliding is reached and the full contact slips.
For an adhesive contact, the shear failure during the incipient stages of sliding friction involves generally a stiction process: a similar zone of microslip develops whose growth is controlled by a complex interplay between friction energy and adhesion.
另外,还可以利用球面-平面几何学研究摩擦动力学。对于光滑球体与平面之间的非粘性负载接触,Mindlin 得出了剪切位移与切向力之间的关系。当剪切位移的振幅增大时,一个微滑动环会从接触区域的边缘向中心扩展,直到达到宏观滑动和完全接触滑动。
对于粘合接触,在滑动摩擦的初始阶段,剪切破坏通常涉及一个粘滞过程:形成一个类似的微滑动区域,其增长受摩擦能和粘合力之间复杂的相互作用控制。
In this Letter, we address the above issues by investigating the shear oscillatory response of solid interfaces coated with weakly adhesive and ultrathin films (~ 1 nm), within the framework of the friction dynamics. The shear contact stiffness and interfacial dissipation before the sliding threshold are determined using the sphere-plane geometry by a resonance method at the $\text{MHz}$ frequency. This work may be relevant for the mechanical behavior and the vibrational dynamics of granular materials. It is also appropriate for the development of microelectromechanical systems where the friction related to the adhesion between solids at low load is a major issue. In this context, our findings would be of practical importance for better understanding the high-frequency tribology.
在这封快讯中,我们在摩擦动力学框架内研究了涂有弱粘合剂和超薄薄膜(约 1 纳米)的固体界面的剪切振荡响应,从而解决了上述问题。利用球面几何结构,通过 $\text{MHz}$ 频率下的共振方法确定了滑动阈值前的剪切接触刚度和界面耗散。这项工作可能与颗粒材料的机械行为和振动动力学有关。它也适用于微机电系统的开发,因为在微机电系统中,低负荷时固体之间的粘附摩擦是一个主要问题。在这种情况下,我们的发现对于更好地理解高频摩擦学具有实际意义。
Experiments
Our experimental setup is depicted Fig. 1(a). The probe in contact with the coated quartz resonator is composed of a calibrated steel sphere of diameter $2R = 2\text{mm}$. To minimize the rotation of the sphere under shear oscillation, the sphere is mounted on a glass capillary vertically aligned on the center of the quartz. The normal load $N$ applied to the interface is 2 mN. The rms roughness of the sphere is about 10 nm as measured by atomic force microscopy on a surface area of $20 \times 20 \mu\text{m}^2$ and that of the quartz is about 1 nm over $10 \times 10 \mu\text{m}^2$.
我们的实验装置如图 1(a)所示。与涂层石英谐振器接触的探头由一个直径为 $2R = 2\text{mm}$ 的经校准的钢球组成。为了尽量减少钢球在剪切振荡下的旋转,钢球被安装在垂直于石英中心的玻璃毛细管上。施加在界面上的法向载荷 $N$ 为 $2\text{ mN}$。通过原子力显微镜测量,在 $20 \times 20 \mu\text{m}^2$ 的表面积上,球体的均方根粗糙度约为 $10\text{ nm}$,而在 $10 \times 10 \mu\text{m}^2$ 的表面积上,石英的均方根粗糙度约为 $1\text{ nm}$。
For preparing the interfaces with the monolayers, the metallized (Au) quartz surface is adsorbed with thiol solutions of mercaptoundecanoic acid or octadecanethiol, resulting in well packed monolayers terminated, respectively, with -COOH (h=1 nm) and -CH3 (h = 2nm) groups, providing a wide range of interfacial energies. These monolayers have a simple hydrocarbon chain, with essentially the same rheological properties as other ubiquitious hydrocarbon films found in the literature.
为了使用单层膜制备界面,金属化(金)石英表面吸附了巯基十酸酐或十八硫醇的硫醇溶液,形成了包装良好的单层膜,分别以 -COOH (h=1 纳米)和 -CH3(h=2 纳米)基团为端基,提供了广泛的界面能。这些单层具有简单的碳氢链,并且其流变特性与文献中发现的其他无规碳氢化合物薄膜基本相同。
Here the surfaces coated with the solid lubricants -CH3 and -COOH are referred to as lubricated, while the unaltered Au and Steel interfaces are referred to as unlubricated or “bare”.
Two systems of interfaces adsorbed with a cured polydimethysiloxane (PDMS) brush (~ 18 and 100 nm) are also prepared for comparison. The PDMS films are adsorbed on the surface by spin coating from heptane solutions, and cured overnight at 90 ℃. The quartz resonator is mounted in a home made cell and all experiments are conducted at 40 ℃ under ambient humidity inside an oven.
在这里,涂有固体润滑剂 -CH3 和 -COOH 的表面被称为 润滑,而未改变的金和钢界面被称为未润滑或 “裸” 界面。
为了进行比较,还制备了两种吸附有固化聚二甲基硅氧烷(PDMS)刷(~ $18$ 纳米和 $100$ 纳米)的界面系统。PDMS 薄膜通过庚烷溶液旋涂吸附在表面,并在 $90$ ℃ 下固化过夜。石英谐振器安装在自制电池中,所有实验均在 $40$ ℃、存在环境湿度的烘箱中进行。
The quartz resonator in shear thickness mode is driven by a network analyzer with the oscillation amplitude $U_{T}$ varying roughly from 0.1 to 5 nm estimated by $U_{T} = CQV$ with $C =1.3\text{ pm/V}$, $Q$ the quality factor of the resonance peak, and $V$ the applied voltage. Before each measurement, the resonator is left in the oven for 30 min until thermal stabilization. Figure 1(b) displays the typical admittance spectra obtained at resonance ~5 MHz before and after the probe is put in contact with the quartz using a microcontrol element. For every contact, the spectral responses associated with four cycles of excitation from low to high amplitude are recorded.
剪切厚度模式下的石英谐振器由网络分析机驱动,振荡幅度 $U_{T}$ 大致在 $0.1$ 到 $5\text{ nm}$ 之间变化,根据 $U_{T} = CQV$ 估算,其中 $C =1.3\text{ pm/V}$,$Q$ 为谐振峰的品质因数,$V$ 为外加电压。每次测量前,谐振器都要在烘箱中放置 $30$ 分钟,直到热稳定为止。图 1(b) 显示了使用微型控制元件将探针与石英接触前后在共振 ~$5\text{ MHz}$ 频率下获得的典型导纳光谱。对于每次接触,都记录了与从低到高振幅的四个激励周期相关的频谱响应。
The response to the first cycle is different from the others (20% error). This dispersion frequently encountered in solid friction stems from a large number of configurations of interfacial pinning sites. When the unsheared junctions are created by bringing the two solids in contact, the initial state of the interface is not reproducible. To the contrary, the first cycle of shearing allows one to prepare the interface in a controlled way. The recorded spectrum for the data analysis is the averaged response over the next three wellcorrelated cycles of excitation, which is in turn averaged on measurements performed with two other different contacts.
第一个周期的响应与其他周期不同(误差为 $20\%$)。这种在固体摩擦中经常出现的分散现象源于大量的界面销钉点构型。当两个固体接触产生非剪切结时,界面的初始状态是不可复现的。相反,第一轮剪切可以让我们以可控的方式制备界面。用于数据分析的记录频谱是接下来三个相关性良好的激励周期的平均响应,而这又是在另外两个不同接触点上进行的测量的平均值。
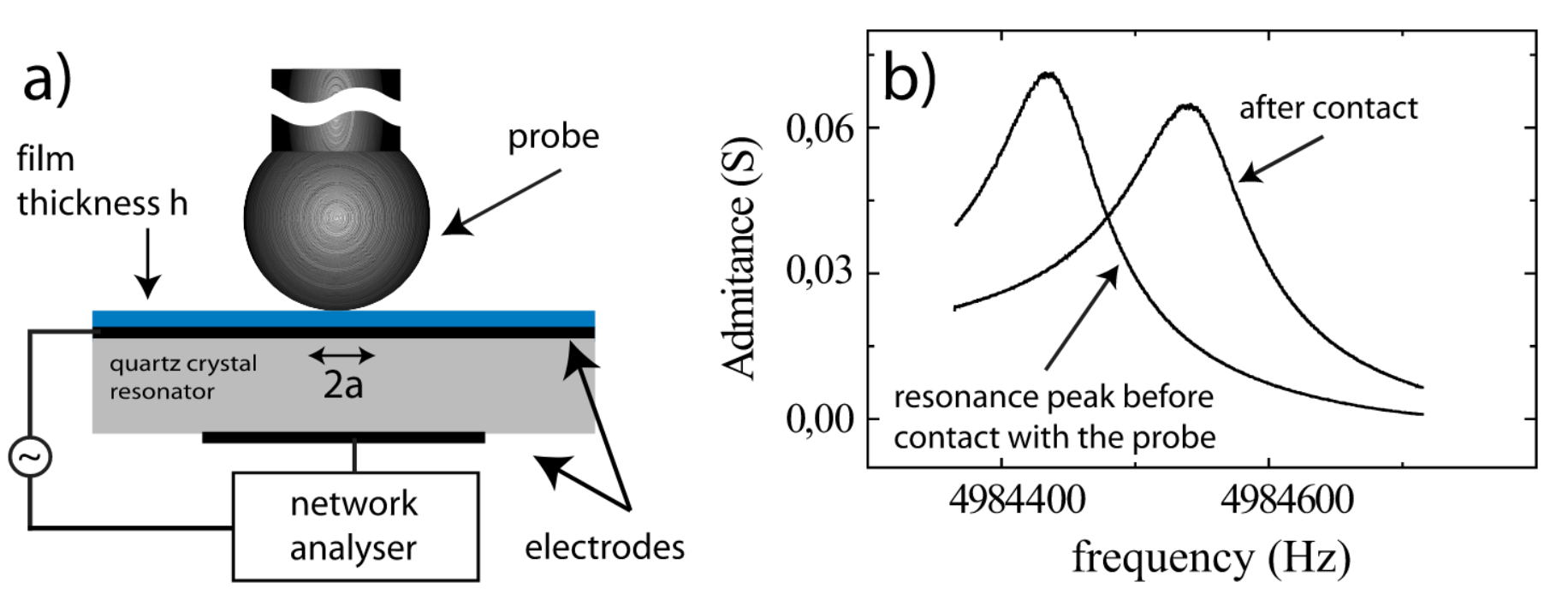
(a) Sketch of the sphere-plane geometry using a quartz resonator. (b) Typical alteration of the resonance peak after contact with the probe.
(a) 使用石英谐振器的球-平面几何草图。(b) 与探针接触后共振峰的典型变化。
The alteration of the resonance peak after the contact between the sphere and the quartz consists of the shift $\Delta f (> 0)$ of the resonance frequency $f_{0}$ and the increase of the inverse quality factor $\Delta Q^{-1}$. They can be related, respectively, to the interfacial stiffness $k_{T} = 4\pi(MK)^{1/2}\Delta f$ and dissipation $\Delta W_{\text{loss}}$ where $M$ and $K$ are the effective mass and stiffness of the quartz and $U_{T}$ is the amplitude of shear displacement.
球体与石英接触后共振峰的变化包括共振频率 $f_{0}$ 的移动 $\Delta f (> 0)$ 和反品质因数 $\Delta Q^{-1}$ 的增加。它们分别与界面刚度 $k_{T} = 4\pi(MK)^{1/2}\Delta f$ 和耗散 $\Delta W_{text{loss}}$ 有关,其中 $M$ 和 $K$ 是石英的有效质量和刚度,$U_{T}$ 是剪切位移的振幅。
Figure 2(a) illustrates both $k_{T}$ and $\Delta Q^{-1}$ measured versus $U_{T}$ for the interface adsorbed with the thick PDMS brush h ~ 100 nm. $k_{T}(=G^{\prime}\pi a^{2}/h)$ and $\Delta Q^{-1}(=G^{\prime\prime}\pi a^{2}/hK)$ (with $G^{\prime}$ and $G^{\prime\prime}$ the elastic and dissipative modulus) are independent of $U_{T}$, indicative of a linear response over the available amplitude range. Such behavior arises probably from the linear viscoelastic properties of the polymer layer bonded at the PDMS-probe interface, expected at the maximum shear strain $\varepsilon_{T}$ ~5%. However, for thinner film h = 18 nm, the stiffness decreases for shear amplitudes larger than $U_{T}$~1 nm.
图 2(a) 展示了在吸附了厚 PDMS 刷子 $h\sim 100\text{ nm}$ 的界面上测量到的 $k_{T}$ 和 $\Delta Q^{-1}$ 与 $U_{T}$ 的关系。$k_{T}(=G^{\prime}\pi a^{2}/h)$ 和 $\Delta Q^{-1}(=G^{\prime\prime}\pi a^{2}/hK)$ ($G^{\prime}$ 和 $G^{\prime\prime}$ 为弹性模量和耗散模量)与 $U_{T}$ 无关,表明在可用的振幅范围内存在线性响应。这种行为可能源于在 PDMS-探针界面处粘合的聚合物层的线性粘弹特性,预计最大剪切应变为 $\varepsilon_{T}$ 5%。然而,对于较薄的薄膜 $h = 18\text{ nm}$,当剪切振幅大于 $U_{T}$$1\text{ nm}$ 时,刚度会降低。
We illustrate this softening by plotting in the inset of Fig. 2(b) the elastic moduli of the 100 nm and 18 nm films versus the effective shear strain $\varepsilon_{\text{eff}} = U_{T}/h$, normalized by the plateau value $G^{\prime}$ when $\varepsilon_{\text{eff}}\rightarrow 0$. Nonlinear behavior of these thin films occurs for $\varepsilon_{\text{eff}} > 10\%$, corresponding to the complex rheological features intermediate between the bulk and boundary properties. Here we will focus on the boundary lubrication regime of the thin films. For the PDMS films less than 10 nm, spinodal decomposition arises after spin coating, preventing the accurate analysis. We therefore pursue our study with the self assembled monolayers.
我们在图 2(b) 的插图中绘制了 $100\text{ nm}$ 和 $18\text{ nm}$ 薄膜的弹性模量与有效剪切应变 $\varepsilon_{text{eff}} = U_{T}/h$ 的关系,并以 $\varepsilon_{\text{eff}}\rightarrow 0$ 时的高原值 $G^{\prime}$ 进行归一化,以说明这种软化现象。在 $\varepsilon_{\text{eff}}> 10%$ 时,薄膜会出现非线性行为,这与介于块体和边界特性之间的复杂流变特性相对应。在此,我们将重点讨论薄膜的边界润滑机制。对于小于 $10\text{ nm}$ 的 PDMS 薄膜,旋涂后会出现自旋分解,从而无法进行精确分析。因此,我们继续研究自组织单层膜。
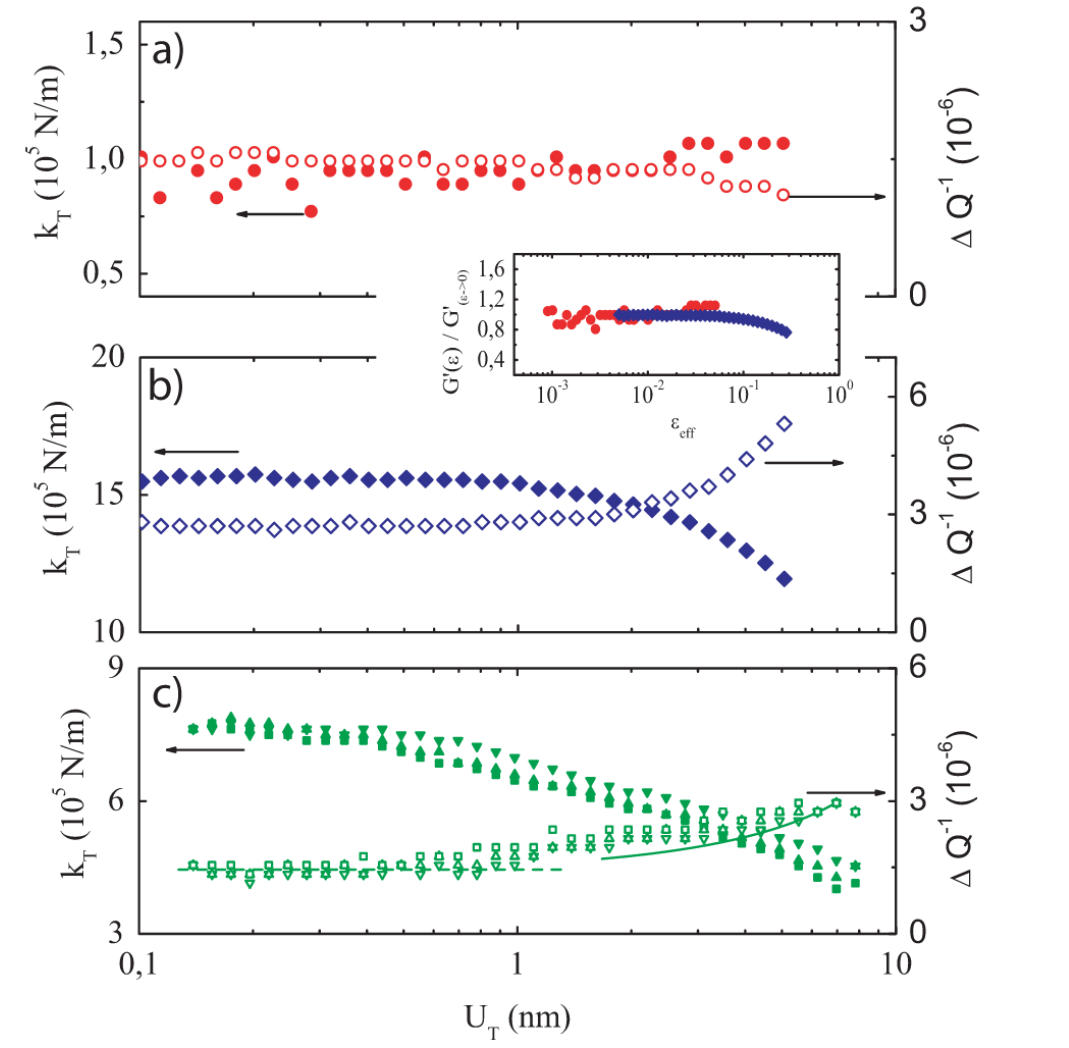
Measured shear stiffness and inverse of quality factor versus shear amplitude at load N = 2 mN. (a) For a PDMS brush of h = 100 nm. (b) For a PDMS brush of h = 18 nm. Inset: Normalized elastic modulus versus shear strain (see text). (c) For a quartz coated with the -CH3 monolayer, three successive runs of measurements are made. The dotted and solid lines correspond to the linear dissipation and $\Delta W$ (see text), respectively.
载荷 $N = 2\text{ mN}$ 时测量到的剪切刚度和品质因数的倒数与剪切振幅的关系。(a) $h = 100\text{ nm}$ 的 PDMS 刷。(b) $h = 18\text{ nm}$ 的 PDMS 刷。插图:归一化弹性模量与剪切应变的关系(见正文)。(c) 对于涂有 -CH3 单层的石英,连续进行了三次测量。虚线和实线分别对应于线性耗散和 $\Delta W$(见正文)。

