Abstract
We study sound propagation in a triangular lattice of spherical beads under isotropic stress. Polydispersity of real beads breaks some contacts, creating a disordered lattice of contacting beads. At large stress, the sound velocity behaves according to Hertz contact law and departs from it at lower stress. This evolution is reversible, with the same crossover when increasing or decreasing the stress, for a given piling. Correlations are much more sensitive to disorder. When calculated with signals propagated in the same lattice, they evolve reversibly with the stress, being much higher at large stress when the contact lattice is more regular. This leads to an interpretation of the non-Hertzian behavior in terms of progressive activation of contacts, in discrepancy with previous models involving buckling of force chains.
我们研究了在各向同性应力作用下,声音在球珠三角晶格中的传播。实际球珠的多分散性破坏了一些接触,形成了一个无序的接触球珠晶格。在大应力下,声速表现为赫兹接触定律,而在较小应力下则偏离该定律。这种演变是可逆的,在增加或减少应力时,对于给定的堆积来说,会出现相同的交叉。相关性对无序性更为敏感。当使用在同一晶格中传播的信号进行计算时,相关性随应力的变化而可逆,当接触晶格更加规则时,相关性在大应力下会更高。这导致了对非赫兹行为的解释,即接触的渐进激活,这与之前涉及力链屈曲的模型不同。
A prominent feature of granular media is the heterogeneity of the spatial distribution of forces in the piling, observed both in simulations and experiments. A lattice of contacting grains supports the stresses and allows acoustic wave propagation. Even for the simplest model of granular media, that is, nominally monodisperse spherical beads whose centers are placed on a regular lattice, the geometry of the contact lattice may be extremely complicated. Indeed, since spherical grains have only point contacts, any imperfections of the beads imply that some contacts are broken, creating randomness.
颗粒介质的一个显著特点是堆积中力的空间各向异性,这在模拟和实验中都能观察到。由相接触颗粒组成的晶格支撑着应力,并允许声波传播。即使是最简单的颗粒介质模型,即中心位于规则晶格上的名义上单分散的球形珠子,接触晶格的几何形状也可能极其复杂。事实上,由于球形颗粒只有点接触,颗粒的任何缺陷都意味着某些接触被破坏,从而产生随机性。
This effect has been set forth to explain the paradoxical propagation of sound in a face-centered cubic lattice of steel beads: Hertz contact law predicts that the sound velocity should scale as the power $1/6$ of the force applied to the piling, whereas a $1/4$ exponent is observed. Some authors suggested that actual beads cannot be considered as perfect elastic spheres. They proposed modifications of Hertz law that led to $1/4$ exponent. Another approach attributes to randomness of the contact lattice the discrepancy with Hertz law predictions.
这种效应被用来解释声音在由钢珠组成的面心立方晶格中传播的矛盾现象:根据 Hertz 接触定律的预测,声速应与施加在堆积上的力的 $1/6$ 幂成比例,而观察到的指数却是 $1/4$。一些学者认为,实际的钢珠不能被视为完美的弹性球体。他们建议对 Hertz 定律进行修正,从而得出 $1/4$ 的指数。另一种方法认为,接触晶格的随机性导致了与 Hertz 定律预测值的差异。
In a previous work, we tested the validity of the first approach on a chain of identical beads, in which all the grains are in contact with their neighbors. Our measurements show Hertzian behavior, which rules out this approach. In this Letter, we report on experiments done with a 2D system, which is adequate to study the consequences of the randomness of the contact lattice.
在之前的工作中,我们在一串相同的珠子上测试了第一种方法的有效性,在这串珠子中,所有的颗粒都与它们的近邻接触。我们的测量结果显示了 Hertz 行为,从而排除了这种方法。在这封快讯中,我们报告了二维系统的实验结果,该系统足以研究接触晶格随机性的后果。
The experimental setup is sketched in Fig. 1. The bead centers are placed on a regular triangular lattice, contained in a hexagonal cell. The lattice is horizontal, held between two plates of polytetrafluoroethylene, in order to get low friction and poor impedance matching between the lattice and the framework.
Three sides of the hexagon are fixed, while the other ones may move independently along their normal direction. The force they exert on the lattice is measured by a static force sensor. With the help of a feedback loop, we may apply a stress at any prescribed value. In the following, the stress is applied isotropically.
实验装置如图 1 所示。珠心放置在一个规则的三角形晶格上,晶格包含在一个六边形单元中。晶格是水平的,夹在两块聚四氟乙烯板之间,以获得晶格和框架之间的低摩擦和低阻抗匹配。
六边形的三个边是固定的,而其他边可以沿其法线方向独立移动。它们对格子施加的力由静态力传感器测量。在反馈回路的帮助下,我们可以施加任意设定值的应力。在下文中,应力是各向同性施加的。
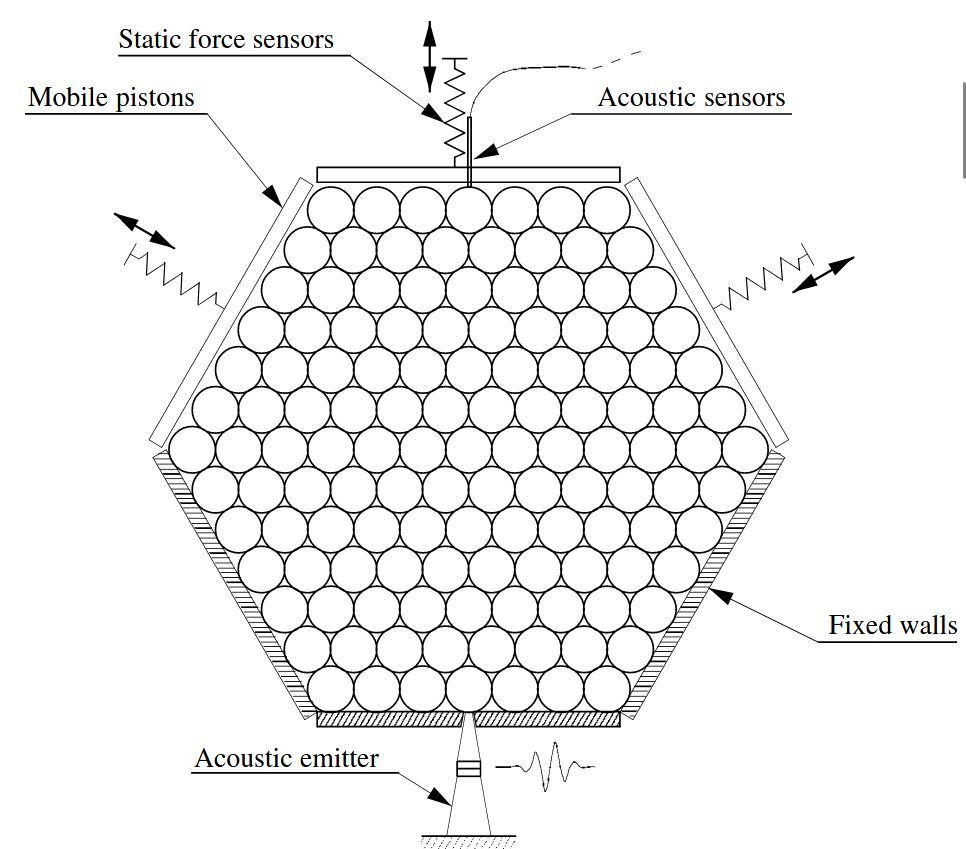
Sketch of the experimental setup.
实验装置草图。
We use either stainless steel beads of diameter $d = 8\text{ mm}\pm 4\mu\text{m}$ or nylon beads ($d = 8\text{ mm}\pm 50\mu\text{m}$). An important feature of our experiment is that both the acoustic transmitter and the sensor are in contact with only one bead. This configuration is particularly sensible to disorder.
我们使用直径为 $d = 8\text{ mm}\pm 4\mu\text{m}$ 的不锈钢珠或尼龙珠($d = 8\text{ mm}\pm 50\mu\text{m}$ )。我们实验的一个重要特点是声发射器和传感器都只与一颗珠子接触。这种构型对于无序性高度敏感。
A carefully designed acoustic transmitter allows us to send a burst wave of well defined frequency 6.5 kHz, with a Gaussian envelope. As shown by Fig. 2, curves (a) and (b), the acoustic signal closely follows the electrical excitation. We measure the time of flight (TOF) of the wave. As we shall see, the arrival of the signal corresponds to the propagation of a coherent wave in an effective medium, so that we can estimate a velocity from the distance between transmitter and sensor.
通过精心设计的声发射器,我们可以发送频率为 $6.5\text{ kHz}$、包络线为高斯的脉冲信号。如图 2 曲线 (a) 和 (b) 所示,声信号紧跟电激励。我们测量波的飞行时间(TOF)。我们将看到,信号的到达与相干波在有效介质中的传播相对应,因此我们可以根据发射器和传感器之间的距离估算出速度。
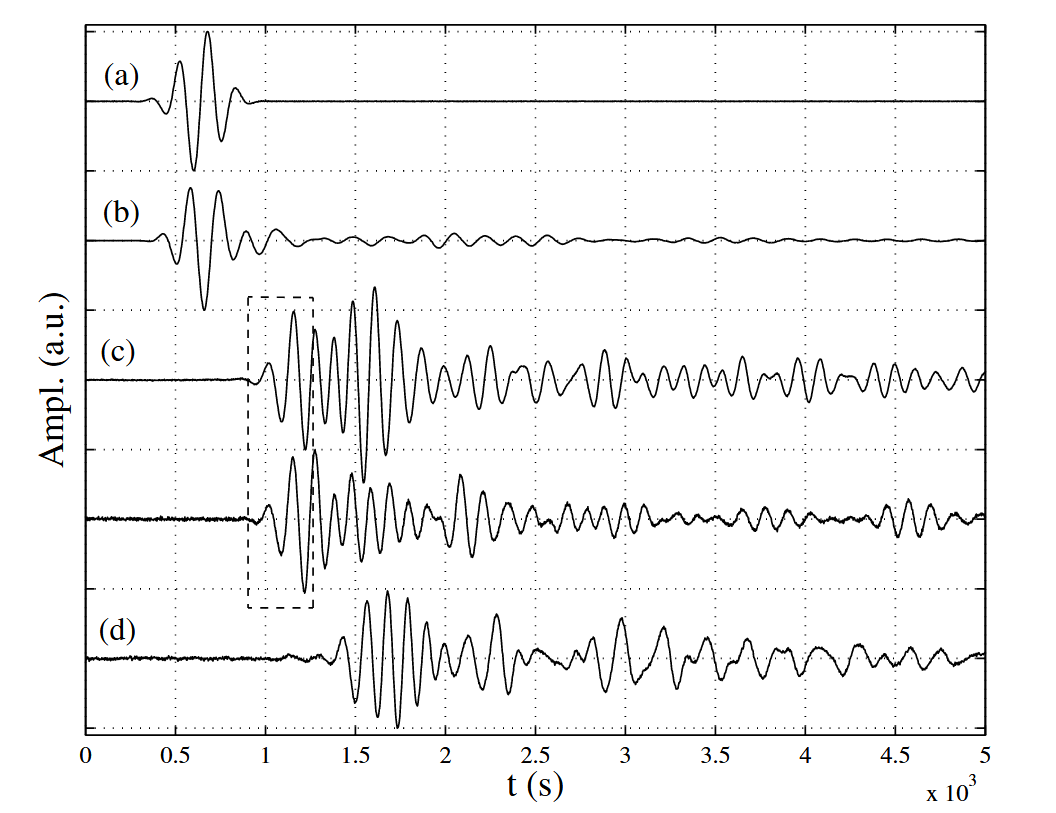
Structure of the signal. Curves: (a) electrical excitation; (b) acoustical response; (c) signals propagated in two different steel bead lattices. The box delimits the coherent signal. Curve (d) shows the signal propagated in nylon beads.
信号结构。曲线:(a) 电激励;(b) 声学响应;(c) 信号在两个不同的钢珠晶格中传播。方框标出了相干信号。曲线 (d) 显示信号在尼龙珠中传播的情况。
The TOF varies between $500$ and $1000 \mu\text{s}$, depending on the applied force (see Fig. 3) in steel beads, and between $900$ and $1400 \mu\text{s}$ (see Fig. 4) in nylon beads. Thus the typical wavelength ranges from $8$ to $16$ (respectively, $6$ to $9$) bead diameters $d$, for steel (respectively, nylon). The lattice side $L$ is $31$ beads, so that the wavelength is intermediate between the two natural length scales $L$ and $d$ of the system, which is consistent with the notion of an effective medium.
钢珠的 TOF 在 $500$ 到 $1000 \mu\text{s}$ 之间变化(取决于施加的力)(见图 3),尼龙珠的 TOF 在 $900$ 到 $1400 \mu\text{s}$ 之间变化(见图 4)。因此,钢珠(对应的是尼龙珠)的典型波长范围为 $8$ 到 $16$(对应的是 $6$ 到 $9$)。晶格边长 $L$ 为 $31d$,因此波长介于系统的两个自然长度尺度 $L$ 和 $d$ 之间,这与有效介质的定义一致。
Each experimental run proceeds in the same way: first, we arrange the beads with their centers on a triangular lattice, thus getting a peculiar (but unknown) initial distribution of bead diameters in the lattice. Then we increase the static force applied on the lattice, without making any measurement: since the lattice holds the stress, the contact network is established. It evolves progressively with the applied force through mechanisms we will detail further.
每次实验都以相同的方式进行:首先,我们将珠子以其中心排列在三角晶格上,从而得到晶格中珠子直径的特定(但未知)初始分布。然后,我们在不进行任何测量的情况下,增加施加在晶格上的静态力:由于晶格能承受应力,接触网络就建立起来了。通过我们将进一步详细介绍的机制,接触网络会随着施加的力逐渐演变。
At the end of this first compression, we get a peculiar realization of the contact lattice. Then, we proceed to the measurements by slowly decreasing the force, each decrement being roughly 10% in magnitude. Having reached the minimal force (below which we are no more able to collect the acoustical signal), we may increase it subsequently in the same way.
在第一次压缩结束时,我们可以看到接触晶格的奇特效果。然后,我们通过缓慢减小力来进行测量,每次减小的幅度大约为 $10\%$。在达到最小力之后(低于该力我们就无法再收集声学信号了),我们可以用同样的方法增加力。
From Fig. 2, curve (c), it is clear that the acoustical signal is strongly distorted after propagation in steel beads. The tail of the signal is partly due to reflections of the waves on the boundaries and partly to multiple scattering by the disordered contact lattice. Wave amplitude is small enough to keep the lattice undisturbed, so that it does not affect the shape of the signal which is perfectly reproducible under constant stress.
从图 2 曲线 (c) 中可以明显看出,声学信号在钢珠中传播后发生了强烈扭曲。信号的尾部部分是由于波在边界上的再反射,部分是由于无序接触晶格的多重散射。波幅很小,足以使晶格不受干扰,因此不会影响信号的形状,信号在恒定应力下完全可以重现。
This is not so when we consider two such measurements for two different initial random mixing of the beads: In that case, the two contact lattices are not the same. As shown in Fig. 2, curve (c), the first oscillations are reproducible, but the tails are completely different, which is an evidence that the wave propagation depends on the details of the contact lattice. We identify those first, reproducible, oscillations as the coherent signal and the tail as the incoherent signal.
如果我们考虑对两种不同的珠子初始随机混合情况进行两次这样的测量,情况就不一样了:在这种情况下,两个接触晶格并不相同。如图 2 曲线 (c) 所示,最初的振荡是可重复的,但尾部却完全不同,这证明波的传播取决于接触晶格的细节。我们将这些可重现的首波振荡称为相干信号,而尾波则称为非相干信号。
For the coherent part of the wave, which propagates in an effective medium, we may define a velocity as the ratio of emittor-sensor distance and the TOF. Its evolution with the static force applied to the piling is shown in Fig. 3. Assuming perfect ordering of the contact lattice, Hertz law predicts a power $1/6$ scaling with the force.
对于在有效介质中传播的相干波,我们可以将速度定义为发射器-传感器距离与 TOF 的比值。图 3 显示了该速度随施加在堆积上的静态力的变化情况。假定接触晶格完美有序,Hertz 定律预示速度与力的幂律指数为 $1/6$。
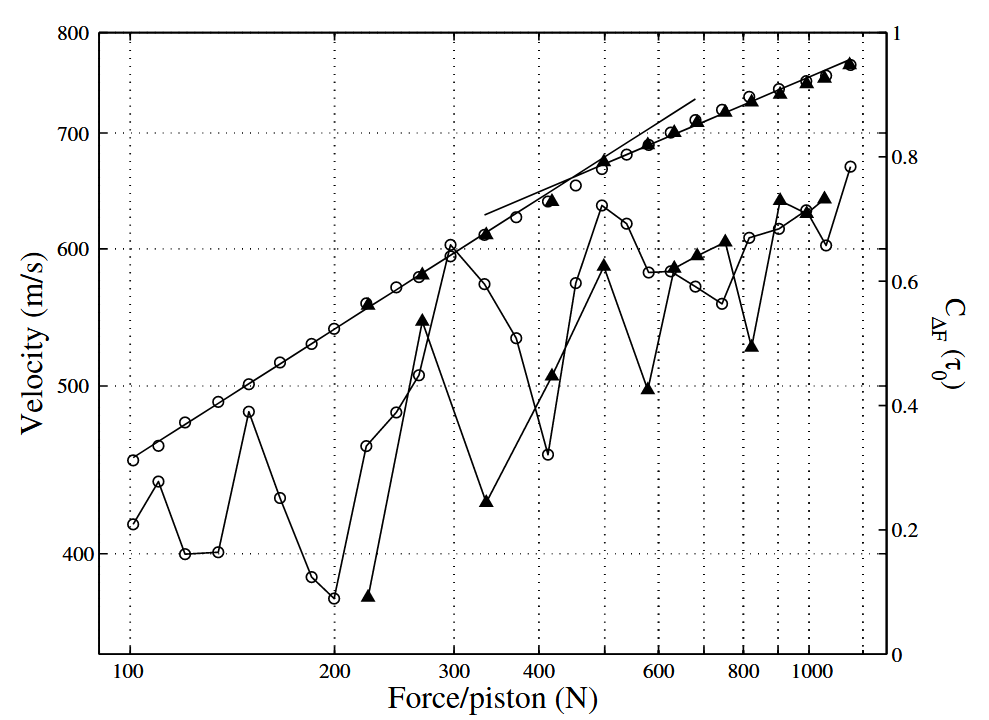
Left ordinate: plot, in log-log scale, of the velocity versus the applied force, in steel beads, during compression ($\circ$) and decompression ($\Delta$) of the same lattice. Right ordinate: plot, in log-linear scale, of the correlation $C_{\Delta F}(\tau_{0})$ [cf. Equation ($\eqref{eq3}$)] (same symbols, joined by a solid line).
左纵坐标:在钢珠中,同一晶格压缩($\circ$)和减压($\Delta$)时的速度与外力的对数线性关系图。右侧纵坐标:相关性 $C_{\Delta F}(\tau_{0})$[cf. Equation ($\eqref{eq3}$)]的对数线性图(符号相同,用实线连接)。
At moderate force we observe a non-Hertzian exponent, followed by a Hertzian one at larger force. What is remarkable is that we observe the same exponent as in 3D systems, roughly $1/4$. This exponent is thus almost insensitive to the piling dimensionality.
The two regimes are always observed with steel beads. The high stress Hertzian regime is very reproducible, with a scaling for the velocity $c_{S} = (255\pm 5)F_{\text{stat}}^{1/6}\text{ m/s}$ (with $F_{\text{stat}}$ in $\text{N}$). The prefactor is in very good agreement with the expected value of $261\text{ m/s/N}^{-1/6}$ for a triangular lattice.
在中等力度下,我们观察到一个非 Hertzian 指数,而在较大力度下则观察到一个 Hertzian 指数。值得注意的是,我们观察到的指数与三维系统中的指数相同,大约为 $1/4$。因此,该指数对堆积的维度几乎不敏感。
在钢珠中始终可以观察到两种状态。高应力 Hertz 体系的可重复性非常高,速度的比例为 $c_{S} = (255\pm 5)F_{\text{stat}}^{1/6}\text{ m/s}$ ($F_{\text{stat}}$ 单位为 $\text{N}$)。前因子与三角形晶格的期望值 $261\text{ m/s/N}^{-1/6}$ 非常吻合。
This is an evidence that, at high stress, the contact lattice becomes more and more homogeneous. In contrast, the crossover between the two regimes strongly depends on the initial lattice and is measured between $190$ and $325\text{ N}$. The amplitude of velocity fluctuations in the nonHertzian regime, at a given force for different initial lattices, is about $20\%$, which is rather small. It illustrates the self-averaging aspect of effective properties such as sound velocity. As we see below, properties of the incoherent part of the signal such as time correlations may fluctuate much more strongly.
这证明在高应力下,接触晶格变得越来越均匀。与此相反,两种状态之间的交叉在很大程度上取决于初始晶格,测量是在 $190$ 和 $325\text{ N}$ 之间进行的。在不同初始晶格的给定作用力下,非 Hertz 机制下的速度波动幅度约为 $20\%$,相当小。这说明了声速这类等效特性的自平均性。正如我们在下文中看到的,信号非相干部分的特性,如时间相关性,可能波动得更强烈。
The non-Hertzian regime reflects the evolution of the contacting grain lattice under compression. Two mechanisms have been put forward to explain this evolution, either successive buckling instabilities of force chains or progressive activation of contacts by elastic deformation of the beads. Buckling occurs only under increasing stress and implies a highly irreversible behavior of the lattice. On the contrary, contact activation is reversible since it relies on the elasticity of the beads.
非 Hertzian 机制反映了接触晶格在压缩条件下的演变。有两种机制可以解释这种演变,一种是力链的连续屈曲不稳定性,另一种是珠粒的弹性变形逐渐激活接触。只有在应力不断增加的情况下才会发生屈曲,这意味着晶格具有高度 不可逆 的行为。相反,接触激活是 可逆 的,因为它依赖于球珠的弹性。
As shown in Fig. 3, the velocity takes the same values during compression or decompression, and most importantly the crossover between Hertzian and non-Hertzian regimes is the same, for a given initial realization of the lattice. This reversible behavior is an evidence that the lattice evolves via activation/deactivation of contacts. Under increasing force contacts are progressively activated, leading to a ramification of the contact lattice, and the effective stiffness of this structure increases more quickly than that of individual contacts. The sound velocity exponent is thus greater than expected from Hertz law. At very large force, almost all grains are in contact and we recover a quasiregular contact lattice and its Hertzian signature.
如图 3 所示,在压缩或减压过程中,速度取值相同,最重要的是,对于给定的晶格初始实现,Hertz 和非 Hertz 状态之间的交叉是相同的。这种可逆的行为证明了晶格是通过触点的激活/失活而演化的。在作用力不断增加的情况下,触点逐渐被激活,从而导致触点晶格的拉伸,这种结构的有效刚度比单个触点的刚度增加得更快。因此,声速指数大于 Hertz 定律的预期值。在非常大的作用力下,几乎所有颗粒都处于接触状态,我们恢复了类线性接触晶格及其 Hertzian 特征。
As evidenced by Fig. 4, the behavior of nylon bead lattice is somewhat different. We observe a new, low force Hertzian behavior. For a given lattice, the evolution of sound velocity is still reversible: velocity values and crossover positions are the same under compression and decompression, even in the new low force regime.
如图 4 所示,尼龙珠晶格的行为有些不同。我们观察到一种新的、低力 Hertz 行为。对于给定的晶格,声速的演变仍然是可逆的:即使在新的低力状态下,声速值和交叉位置在压缩和减压时也是相同的。
From the Hertz solution, one can roughly estimate the ratios of the distances of approach $\delta$ for steel and nylon beads,
$$ \frac{\delta_{\text{nylon}}}{\delta_{\text{steel}}} = \left(\frac{E_{\text{steel}}}{E_{\text{nylon}}} \frac{F_{\text{nylon}}}{F_{\text{steel}}}\right)^{2/3}\approx 4 $$
根据 Hertz 解,我们可以大致估算出钢珠和尼龙珠的接近距离 $\delta$ 的比率:
$$ \frac{\delta_{\text{nylon}}}{\delta_{\text{steel}}} = \left(\frac{E_{\text{steel}}}{E_{\text{nylon}}} \frac{F_{\text{nylon}}}{F_{\text{steel}}}\right)^{2/3}\approx 4 $$
where $F_{\text{steel}}$ (respectively, $F_{\text{nylon}}$) is the midscale force taken from Fig. 3 (respectively, Fig. 4), and $E$ is the Young’s modulus ($E = 2.26\times 10^{11}\text{ N/m}^{2}$ for steel and $E = 3.55\times 10^{9}\text{N/m}^{2}$ for nylon). Thus the increase of the distance of approach for nylon beads is insufficient to compensate the factor 10 in radius dispersion. Hence the initial tenuous structure which holds the stress under very low compression is much more stable in nylon than in steel beads. Under increasing stress, it first evolves elastically, without much new contacts, causing this low force Hertzian regime. Then, more contacts are activated and we recover the non-Hertzian regime already observed with steel beads.
其中,$F_{\text{steel}}$(分别为 $F_{\text{nylon}}$)是取自图 3(分别为图 4)的中值力,$E$ 是杨氏模量 (对于钢,$E = 2.26\times 10^{11}\text{ N/m}^{2}$; 对于尼龙,$E = 3.55\times 10^{9}\text{N/m}^{2}$)。因此,尼龙珠接近距离的增加不足以补偿半径分散的 $10$ 倍。因此,与钢珠相比,尼龙珠在极低压缩下保持应力的初始脆弱结构要稳定得多。在应力不断增加的情况下,它首先会发生弹性演变,而不会产生太多新的接触,从而形成这种低力 Hertzian 状态。然后,更多的接触被激活,我们恢复了在钢珠中已经观察到的非 Hertzian 状态。
As with steel beads, the high stress Hertzian regime is very reproducible, with an experimental prefactor $227\pm 5\text{ m/s/N}^{-1/6}$ in very good agreement with the calculated one $233\text{ m/s/N}^{-1/6}$. The crossover positions strongly depend on the initial lattice, ranging, respectively, from 15 to 25 N and from 50 to 60 N.
与钢珠一样,高应力 Hertzian 机制的重现性非常好,实验前因子 $227\pm 5\text{ m/s/N}^{-1/6}$ 与计算值 $233\text{ m/s/N}^{-1/6}$ 非常一致。交叉位置在很大程度上取决于初始晶格,范围分别为 $15$ 到 $25\text{ N}$ 和 $50$ 到 $60\text{ N}$。
A low force Hertzian behavior has been predicted by Roux in simulations of our experimental system. He observed it for $\frac{2P}{\alpha^{3/2}Ed} < 10^{-3}$, where $P$ is the 2D pressure and $\alpha$ is the relative dispersion in diameter. This gives an estimate of, respectively, 7 N (for steel) and 2 N (for nylon) as the crossover between low force Hertzian and non-Hertzian behaviors. Our measurements are in qualitative agreement with this prediction, since we go down to much lower forces with nylon beads than with steel beads. But the corresponding crossover observed with nylon bead lattice is 20 N. A possible explanation of this discrepancy is friction between grains, not taken into account in the simulations.
Roux 在模拟我们的实验系统时预测到了低力赫兹行为。他观察到,当 $\frac{2P}{\alpha^{3/2}Ed}< 10^{-3}$,其中 $P$ 是二维压力,$\alpha$ 是直径的相对分散。据此估算,低力赫兹和非赫兹行为的交叉点分别为 $7\text{ N}$(钢)和 $2\text{ N}$(尼龙)。我们的测量结果与这一预测基本一致,因为尼龙珠的作用力比钢珠小得多。但在尼龙珠晶格中观察到的相应分界点为 $20\text{ N}$。造成这种差异的可能原因是模拟中没有考虑到晶粒之间的摩擦。
Recently, a new theoretical approach has been used to calculate the effective speed of sound in the same system. This mean field calculation, valid in the high force limit where force fluctuations are not too strong, takes into account the evolution of the number of effective contacts with the pressure exerted on the lattice. The sound velocity as a function of the pressure agrees very well with our data and the simulations of Roux, at moderate or high pressure. As emphasized in [14], this analytical solution cannot be simply writen as a power law.
最近,一种新的理论方法被用于计算同一系统中的有效声速。这种平均场计算方法在力波动不太大的高力极限下有效,它考虑到了有效接触点数量随施加在晶格上的压力而变化的情况。声速与压力的函数关系与我们的数据和 Roux 的模拟结果非常吻合,在中等或较高压力下都是如此。正如文献 [14] 所强调的,这种解析解不能简单地写成幂律。
To compare signal shapes, particularly sensitive to disorder, we use cross correlations. If each signal consists in $N$ samples $s_{i}(t_{n})$ taken at times $t_{n}$, it reads
$$ C^{1,2} = \frac{\sum_{n = 1}^{N}s_{1}(t_{n})s_{2}(t_{n})}{\sqrt{\sum_{n = 1}^{N}s_{1}^{2}(t_{n})}\sqrt{\sum_{n = 1}^{N}s_{2}^{2}(t_{n})}} $$
We restrict this calculation either to the coherent signal, denoting $C_{\text{coh}}$, or to the acoustic speckle, denoting $C_{\text{incoh}}$. The correlations are calculated at the same static force, either for the same lattice under compression and decompression ($C^{\approx}$) or for two lattices with different initial preparation ($C^{\neq}$).
为了比较信号形状(对无序特别敏感),我们使用了交叉相关(函数)。如果每个信号由 $N$ 个采样 $s_{i}(t_{n})$ 组成,取样时间为 $t_{n}$,则其为
$$ C^{1,2} = \frac{\sum_{n = 1}^{N}s_{1}(t_{n})s_{2}(t_{n})}{\sqrt{\sum_{n = 1}^{N}s_{1}^{2}(t_{n})}\sqrt{\sum_{n = 1}^{N}s_{2}^{2}(t_{n})}} $$
我们将计算局限于相干信号(表示为 $C_{\text{coh}}$)或声学斑点(表示为 $C_{\text{incoh}}$)。相关性是在相同的静态力下计算的,可以是压缩和减压下的同一晶格($C^{\approx}$),也可以是初始准备不同的两个晶格($C^{\neq}$)。
The results are summarized in Fig. 5. The correlations $C_{\text{coh}}^{\approx}$ and $C_{\text{coh}}^{\neq}$ are always greater than $0.8$. This is consistent with the concept of coherent signal, whose properties depend only on the effective propagation medium, not on the details of the contact lattice.
In contrast, the correlations $C_{\text{incoh}}^{\approx}$ and $C_{\text{incoh}}^{\neq}$ are smaller, and we always have $C_{\text{incoh}}^{\neq} < C_{\text{incoh}}^{\approx}$. For lattices with different initial statistical distributions of beads, $C_{\text{incoh}}^{\neq}$ is small.
图 5 总结了这些结果。相关系数 $C_{\text{coh}}^{\approx}$ 和 $C_{text{coh}}^{\neq}$ 总是大于 $0.8$。这与相干信号的概念是一致的,相干信号的特性只取决于有效的传播介质,而不取决于接触晶格的细节。
相反,相关系数 $C_{\text{incoh}}^{\approx}$ 和 $C_{\text{incoh}}^{\neq}$ 较小,我们总是看到 $C_{\text{incoh}}^{\neq} < C_{\text{incoh}}^{\approx}$。对于具有不同珠子初始统计分布的网格,$C_{\text{incoh}}^{\neq}$ 是很小的。
It is remarkable that this effect persists far away in the Hertzian regime, showing that correlations are a much more sensitive probe than velocity measurements and that some disorder remains even with high applied forces. On the contrary, waves propagating during compression and decompression of the same lattice are highly correlated. It is another evidence of reversibility and that buckling of force chains is not the relevant phenomenon for the evolution of the contact lattice.
值得注意的是,这种效应在 Hertz 状态下依然存在,这表明相关性是比速度测量更灵敏的探针,而且即使施加了很大的力,一些无序性依然存在。相反,同一晶格在压缩和减压过程中传播的波具有高度相关性。这再次证明了接触晶格的可逆性,以及力链的屈曲并不是接触晶格演变的相关现象。
In our confined setup, the tail of the signal originates both from multiple scattering in a disordered medium and from multiple reflections on the boundaries. Since reflection holds on fixed boundaries and involves mostly the coherent signal, it should not depend much on the details of the lattice.
On the contrary, the weak values of $C_{\text{incoh}}^{\neq}$ (see Fig. 5) show that the incoherent signal highly depends on lattice configuration. That means that multiple scattering is predominantly responsible for its structure and justifies a posteriori to call it incoherent.
在我们的密闭设置中,信号尾波既来自无序介质中的多重散射,也来自边界上的多重再反射。由于再反射在固定边界上成立,并且主要涉及相干信号,因此它不应该太依赖于晶格的细节。
相反,$C_{\text{incoh}}^{\neq}$ 的弱值(见图 5)表明非相干信号高度依赖于晶格构型。这意味着多重散射是造成其结构的主要原因,因此可以后验地将其称为非相干信号。
To describe the contact lattice evolution with the force, we calculate the correlation for two successive forces $F$ and $F + \Delta F$, during a monotonic evolution of the stress,
$$ C_{\Delta F}(\tau_{0}) = \frac{\sum_{n = 1}^{N}s_{F}(t_{n})s_{F+\Delta F}(t_{n} + \tau_{0})}{\sqrt{\sum_{n = 1}^{N}s_{F}^{2}(t_{n})}\sqrt{s_{F + \Delta F}^{2}(t_{n})}} $$
Here $\tau_{0}$ is the delay caused by the sound velocity variation due to the force increment $\Delta F$. As shown by Fig. 3, the correlation is much higher in the high force Hertzian regime, which supports our previous interpretation: at large force, almost all contacts are active, the lattice evolves very little under a force increment, and the correlation should be high. On the contrary, it is small in the non-Hertzian regime where the lattice evolves a lot by progressive activation of contacts. The reproducibility of the correlation under compression and decompression indicates that the contact lattice evolves reversibly.
为了描述接触晶格随力的演变,我们计算了应力单调演变过程中两个连续力 $F$ 和 $F + \Delta F$ 的相关性:
$$ C_{\Delta F}(\tau_{0}) = \frac{\sum_{n = 1}^{N}s_{F}(t_{n})s_{F+\Delta F}(t_{n} + \tau_{0})}{\sqrt{\sum_{n = 1}^{N}s_{F}^{2}(t_{n})}\sqrt{s_{F + \Delta F}^{2}(t_{n})}} $$
这里的 $\tau_{0}$ 是由力增量 $\Delta F$ 引起的声速变化造成的延迟。如图 3 所示,相关性在高力赫兹机制下要高得多,这支持了我们之前的解释:在大力条件下,几乎所有的接触都是活跃的,晶格在力增量下的演化非常小,相关性应该很高。相反,在非 Hertz 机制下,由于接触的逐渐激活,晶格发生了很大变化,因此相关性很小。相关性在压缩和减压条件下的再现性表明,接触晶格的演变是可逆的。
We have shown that a regular lattice of nominally identical beads actually behaves as a disordered system. The sound velocity dependency on the stress is steeper than what may be expected from Hertzian behavior of a perfect lattice. This is due to structural modification of the contact lattice, via progressive activation of contacts. The reversibility of this process is evidenced by the lack of hysteresis in both velocity and correlation measurements during compression/decompression of the system. This is presumably true for more general granular media.
我们已经证明,由名义上相同的球珠组成的 规则 晶格实际上表现为一个 无序 系统。与完美晶格的 Hertz 行为相比,声速与应力的关系更为陡峭。这是由于接触晶格通过接触的逐渐激活而发生了结构性改变。在系统压缩/减压过程中,速度测量和相关测量都没有滞后现象,这证明了这一过程的可逆性。这可能适用于更一般的颗粒介质。

