Abstract
Granular flows triggered by vibration below the avalanche angle are ubiquitous in nature. However, the mechanism of triggering and the nature of the resulting flow are not fully understood. Here we investigate the triggering of the shear instability of granular layers by nanometer-amplitude ultrasound close to the static threshold.
We find that such small-amplitude and high-frequency sound waves provoke unjamming, resulting in a self-accelerated inertial flow or a creeplike regime which stops flowing after the removal of ultrasound. We show that these effects are due to the reduction of interparticle friction at grain contacts by the shear acoustic lubrication. Our observations are consistent with the bistability inherent to velocity-weakening friction models [e.g., Jaeger et al., Europhys. Lett. 11, 619 (1990)]. This work should help to understand the local and remote triggering of landslides and earthquakes by seismic waves.
由振动引发的低于雪崩角的颗粒流在自然界无处不在。然而,人们对其触发机制和所产生的流动性质并不完全了解。在这里,我们研究了纳米振幅超声波在接近静态阈值时触发颗粒层剪切不稳定性的问题。
我们发现,这种小振幅、高频率的声波会引发解堵塞,导致自加速惯性流动或蠕变状态,在超声消除后停止流动。我们的研究表明,这些效应是由于剪切声润滑减少了晶粒接触处的颗粒间摩擦。我们的观察结果与速度减弱摩擦模型固有的双稳态一致[例如 Jaeger 等人, Europhys. Lett. 11, 619 (1990)]. 这项工作有助于理解地震波对滑坡和地震的局部和远程触发。
Introduction
Laboratory studies of the frictional instability in sheared granular media have emerged as a powerful tool for investigating dynamics of seismic faults, landslides, and avalanches [Figs. 1(a) and 1(b)]. An important and challenging issue in seismic hazard is to understand the remote dynamics triggering of earthquake by impinging seismic (elastic) waves at microstrain amplitude. Moreover, recent observations showed that perturbations from local foreshocks activities are probably a part of the earthquake nucleation process and that large rockfall events and avalanches can be triggered by volcanic seismicity.
剪切颗粒介质摩擦不稳定性的实验室研究已成为研究地震断层、滑坡和雪崩动力学的有力工具[图 1(a) 和 1(b)]。地震灾害中一个重要而具有挑战性的问题是了解微应变振幅的地震(弹性)波冲击引发地震的长程动力学。此外,最近的观测表明,局部前震活动的扰动可能是地震成核过程的一部分,火山地震也可能引发大型落石事件和雪崩。
Indeed, dynamic stress from seismic waves can perturb fault systems that are close to the yield stress, e.g., due to tectonic stresses $\tau\leq \tau_{S}$ [Fig. 1(c)], and force failure earlier in time relative to an unperturbed fault or cliff. Understanding the mechanics of local and remote triggering of landslides will go a long way in quantifying seismic hazard.
事实上,地震波产生的动态应力可以扰动接近屈服应力的断层系统,例如,由于构造应力 $\tau\leq \tau_{S}$ [图 1(c)],相对于未受扰动的断层或悬崖,迫使其提前破坏。了解滑坡的局域和长程触发机制将大大有助于量化地震灾害。
Advances in granular physics and acoustics have paved the way for understanding how and under what conditions impinging seismic waves may trigger a fault slip. A granular medium is an assembly of discrete macroscopic solid grains that interact with each other by dissipative contact forces.
Unlike ordinary solids and liquids, static and dynamic properties of dense granular media are determined by inhomogeneous contact force networks, exhibiting multiple metastable configurations.
颗粒物理学和声学的进步为了解冲击地震波如何以及在何种条件下可能引发断层滑动铺平了道路。颗粒介质是离散的宏观固体颗粒的聚合体,它们通过耗散性的接触力相互作用。
与普通固体和液体不同,致密颗粒介质的静态和动态特性是由不均匀的接触力网络决定的,表现出多种亚稳态构型。
Sound waves propagating from grain to grain provide not only a unique probe of such networks (often opaque) but also a controlled perturbation via elastic softening and frictional dissipation. Granular media undergo a transition from a jammed solid state to a flowing liquid state when the external shear exceeds the static yield stress.
声波从一个颗粒传播到另一个颗粒,不仅为这种(力)网络(通常是不透明的)提供了独特的探测手段,而且还通过弹性软化和摩擦耗散提供了可控的扰动。当外部剪切力超过静态屈服应力时,颗粒介质会从堵塞固态转变为流动液态。
Theoretical and experimental studies suggest that this transition is a subcritical bifurcation [sketched in Fig. 1(d)], with dynamics similar to solid friction at multicontact interfaces [insets of Figs. 1(a) and 1(b)] well-described by the rate and state constitutive law by Dieterich, Rice, and Ruina.
Burridge and Knopoff have also used this kind of velocity-weakening friction in their spring-block model to describe the earthquake stick-slip dynamics. Here, we define $\mu = \tau/\sigma_{n} = F_{t}/F_{n}$ the shear stress (force) normalized by the normal stress (force) from which the static and dynamic coefficients of friction $\mu_{S,d} = \tau_{S,d}/\sigma_{n} = F_{S,d}/F_{n}$ follow.
理论和实验研究表明,这种转变是一种亚临界分支[如图 1(d)所示],其动力学类似于多接触界面上的固体摩擦[图 1(a)和 1(b)的插图],由 Dieterich、Rice 和 Ruina 的速率和状态本构定律很好地描述。
Burridge 和 Knopoff 在他们的弹簧块模型中也使用了这种速度减弱摩擦来描述地震粘滑动力学。在这里,我们定义 $\mu = \tau/\sigma_{n} = F_{t}/F_{n}$ 为通过法向应力(力)归一化的剪应力(力),静($S$)/动($d$)摩擦系数 $\mu_{S,d} = \tau_{S,d}/\sigma_{n} = F_{S,d}/F_{n}$ 由此而来。
Here $\tau_{S}$ and $F_{S}$ are the static friction stress and force at yield while $\tau_{d}$ and $F_{d}$ are the dynamic friction stress and force. In the inclined plane geometry of angle $\theta$ such as in the present study [Fig 1(b)], we have $\mu=\tan{\theta}$ and $\mu_{S} = \tan{\theta_{m}}$, with $\theta_{m}$ the (maximum) angle of avalanche. The angle of repose $\theta_{r}$ being a few percent lower than $\theta_{m}$ corresponds to the dynamic friction $\mu_{d} = \tan{\theta_{r}}$ at the minimum shear load [Fig. 1(d)].
这里的 $\tau_{S}$ 和 $F_{S}$ 是屈服时的静摩擦应力和力,而 $\tau_{d}$ 和 $F_{d}$ 是动摩擦应力和力。在角度为 $\theta$ 的倾斜平面几何中,例如在本研究中[图 1(b)],我们有 $\mu=\tan{\theta}$ 和 $\mu_{S} = \tan{\theta_{m}}$,其中 $\theta_{m}$ 为(最大)雪崩角。与最小剪切荷载下的动摩擦力 $\mu_{d} = \tan{\theta_{r}}$ 相对应,倾角 $\theta_{r}$ 比 $\theta_{m}$ 小几个百分点[图 1(d)]。
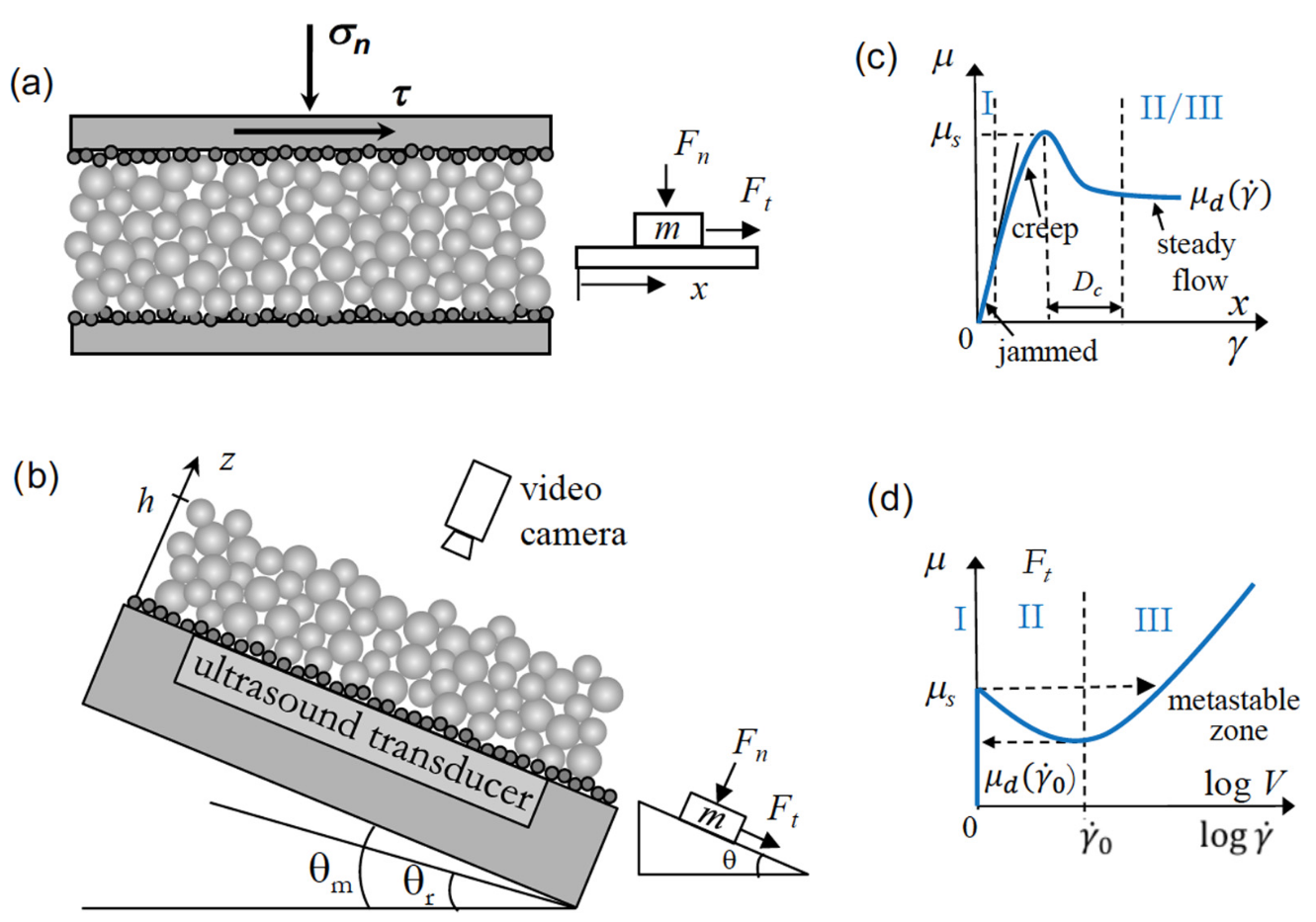
(a) Schematic cross section of a granular layer under shear (e.g., fault gouge). (b) Flow of a granular layer on an inclined plane at angle $\theta$ . The angle of avalanche is $\theta_{m}$ and the angle of repose is $\theta_{r}$. (c) Typical plot of the normalized shear stress (force) $\mu = \tau /\sigma_{n} = F_{t}/F_{n}$ vs strain $\gamma$ or displacement $x$. Region $\text{I}$ corresponds to the jammed state with a linear elastic response. It is followed by slow creep motion when approaching the threshold $\mu_{S}$. After yielding, the system slides over a characteristic distance $D_{c}$ before reaching the steady flow at a velocity or rate imposed by shear load; as shown in (d) it can be stable ($\text{III}$) or unstable ($\text{II}$). (d) Typical plot of $\mu$ vs flow rate $\dot{\gamma}$ or velocity $V$ with the different states as in (c). Region $\text{I}$ appearing as a vertical line corresponds to the jammed state, region $\text{II}$ ($\dot{\gamma} < \dot{\gamma}_{0}$) to the unstable intermittent flow/slip, and region $\text{III}$ ($\dot{\gamma}>\dot{\gamma}_{0}$) to the stable inertial flow/slip where $\dot{\gamma}_{0}$ is the shear rate corresponding to the minimum friction.
(a) 受剪切力作用的颗粒层(如断层破碎带)的横截面示意图。(b) 倾角为 $\theta$ 的颗粒层在倾斜平面上的流动。雪崩角为 $\theta_{m}$,休止角为 $\theta_{r}$。(c) 归一化剪应力(力)$\mu = \tau /\sigma_{n} = F_{t}/F_{n}$ 与应变 $\gamma$ 或位移 $x$ 的典型图。区域 $\text{I}$ 对应于线性弹性响应的堵塞状态。当接近阈值 $\mu_{S}$ 时,随之而来的是缓慢的蠕变运动。屈服后,系统滑过一个特征距离 $D_{c}$,然后以剪切载荷施加的速度或速率达到稳定流动;如 (d) 所示,它可以是稳定的($\text{III}$),也可以是不稳定的($\text{II}$)。(d) $\mu$ 与流速 $\dot{\gamma}$ 或速度 $V$ 的典型关系图,不同状态如 (c) 所示。以垂直线出现的 $\text{I}$ 区域对应于堵塞状态,$\text{II}$($\dot{\gamma} < \dot{\gamma}_{0}$)区域对应于不稳定的间歇流动/滑动、和区域 $\text{III}$($\dot{\gamma}>\dot{\gamma}_{0}$)为稳定的惯性流动/滑动,其中 $\dot{\gamma}_{0}$ 是最小摩擦力对应的剪切速率。
Previous works showed that for shear forces far below the threshold $\mu < \mu_{S}$, both granular layers and rough solid interfaces [Figs. 1(a), 1(b), and insets] respond elastically as shown in Fig. 1(c), via the reversible deformation of contacting grains or/and asperities, in the jammed state (region $\text{I}$). For $\mu\leq\mu_{S}$, nonlinear response occurs with creeplike irreversible sliding. For $\mu\geq\mu_{S}$, the system yields and starts to slide over a transient characteristic distance $D_{c}$ (slip weakening) before reaching the steady-flow region $\text{II}$/$\text{III}$ at a velocity $V$ or shear rate $\dot{\gamma}$ imposed by the load (to be described in the following).
之前的研究表明,当剪切力远小于阈值 $\mu < \mu_{S}$ 时,颗粒层和粗糙固体界面[图 1(a)、1(b)和插图]都会如图 1(c)所示,通过接触颗粒或/和(表面)微凸的可逆变形,在堵塞状态(区域 $\text{I}$)下发生弹性响应。对于 $\mu\leq\mu_{S}$,非线性响应与蠕变式不可逆滑动同时发生。对于 $\mu\geq\mu_{S}$,系统屈服并开始滑动,滑动距离为瞬态特征距离 $D_{c}$(滑动减弱),然后以负载施加的速度 $V$ 或剪切速率 $\dot{\gamma}$(将在下文中描述)到达稳定流动区域 $\text{II}$/$\text{III}$。
In the representation $\mu = \mu(V)$ or $\mu(\dot{\gamma})$ plotted in Fig. 1(d), the velocity weakening region ($\dot{\gamma} < \dot{\gamma}_{0}$), referred to as “$\text{II}$”, is unstable and can lead to intermittent flow behavior (e.g., stick-slip). Such frictional instability results from an aging-rejuvenation competition acting within the micrometer-sized contacting asperities, which can also be modeled by the micro- or nanoblocks coupled elastically by springs. For high flow rates ($\dot{\gamma} > \dot{\gamma}_{0}$), the slope of $\mu(\dot{\gamma})$ is positive and ensures the stability of the steady flow as in region $\text{III}$.
在图 1(d) 中绘制的 $\mu =\mu(V)$ 或 $\mu(\dot{\gamma})$ 表示中,速度减弱区域($\dot{\gamma} < \dot{\gamma}_{0}$),即"$\text{II}$",是不稳定的,可能导致间歇性流动行为(例如,粘滑)。这种摩擦不稳定性源于微米级接触微凸内部的老化-再生竞争,也可以通过弹簧弹性耦合的微块或纳米块来模拟。对于高流速($\dot{\gamma} > \dot{\gamma}_{0}$),$\mu(\dot{\gamma})$ 的斜率为正,并确保稳定流动的稳定性,如在 $\text{III}$ 区域。
The possible failure of a granular medium, such as the sandpile, caused by external vibrations, has been known for a long time in engineering and geophysical applications, however a unified physical description still lacks. The vibrations considered are most of the time of large-amplitude $U_{0}\geq d$ with $d$ the grain size and low-frequency $f < f_{0}$. where $f_{0}$ is a characteristic frequency determined by the stiffness of Hertzian contacts. The amount of shaking is usually estimated by the reduced peak acceleration of the grain $\Gamma = a/g = (2\pi f)^{2}U_{0}/g$ with $g$ the gravity.
在工程和地球物理应用中,人们很早就知道外部振动可能导致砂堆等颗粒介质破坏,但仍然缺乏统一的物理描述。所考虑的振动大多数情况下是大振幅 $U_{0}\geq d$,其中 $d$ 为粒度,低频 $f < f_{0}$,其中 $f_{0}$ 是由赫兹接触刚度决定的特征频率。摇晃程度通常通过颗粒的加速度峰值 $\Gamma = a/g = (2\pi f)^{2}U_{0}/g$ 来估算,其中 $g$ 为重力。
When $\Gamma > 1$, vertical vibrations cancel almost normal forces exerting on the grain (confined under gravity) and modify consequently the spatial arrangement of grains, resulting in phenomena such as compaction, convection, shear banding, to mention a few. This is similar to the oscillation effect on the normal stress facilitating sliding and also to the scenario of the acoustic fluidization in a confined continuous medium.
当 $\Gamma > 1$ 时,垂直振动几乎抵消了施加在颗粒上的法向力(重力约束),从而改变了晶粒的空间排列,产生了压实、对流、剪切带等现象。这与促进滑动的法向应力的振荡效应相似,也与封闭连续介质中的声波流化情景相似。
In this scenario, the acoustic pressure $p_{a} = (\rho c)v_{a}$, with $c$ the sound speed and $v_{a}$ the vibration velocity, is expected to temporally relieve the pressure of the overburden, thereby decreasing the yield stress. For horizontal vibrations, whenever $\Gamma > \mu$, the grains in the top layers of free surface slide against each other akin to the slider on an inclined frictional plane.
在这种情况下,声压 $p_{a} = (\rho c)v_{a}$ (其中 $c$ 为声速,$v_{a}$ 为振速)有望暂时缓解覆盖层的压力,从而降低屈服应力。对于水平振动,只要 $\Gamma > \mu$,自由表面顶层的颗粒就会相对滑动,类似于倾斜摩擦面上的滑块。
Other studies claim that shaking should be parametrized by the vibration velocity $v_{a} = (2\pi f)U_{0}$ squared, because the vibrations interact with the medium in terms of a granular temperature $T_{g}$ proportional to the kinetic energy of the grain $T_{g}\sim (1/2)mv_{a}^{2}$ with $m$ the grain mass. More recent works suggest rather a collisionlike pressure term, $p_{c}\sim (1/2)\rho v_{a}^{2}$ with $\rho$ the granular mass density.
其他研究认为,振动应该以振动速度 $v_{a} = (2\pi f)U_{0}$ 的平方为参数,因为振动与介质相互作用的颗粒温度 $T_{g}$ 与颗粒动能成正比 $T_{g}\sim (1/2)mv_{a}^{2}$ ,其中 $m$ 为颗粒质量。最近的研究提出了一个类似碰撞的压力项,$p_{c}\sim (1/2)\rho v_{a}^{2}$,其中 $\rho$ 为颗粒质量密度。
However, the above scenarios, involving large-amplitude vibrations, cannot explain the dynamic earthquake triggering by seismic waves at micro- and nanostrain amplitude, nor the laboratory experiments using nanometer-amplitude ultrasound to soften the material modulus by $30\%$ via nonlinear dynamics. Also, some modifications of the stick-slip cycle by ultrasound remain unexplained.
然而,上述涉及大振幅振动的方案无法解释微应变和纳米应变振幅的地震波引发的动态地震,也无法解释利用纳米振幅超声波通过非线性动力学使材料模量软化 $30\%$ 的实验室实验。此外,超声波对粘滑循环的一些影响尚未得以解释。
In these situations, the oscillation frequency of ultrasound $f \geq 40\text{ kHz}$ is high compared to the characteristic frequency $f_{0}\sim 5\text{ kHz}$ in millimeter-thick granular layers so that grains cannot have normal motion, due to inertia, in order to suppress the weight of the overburden.
On the other hand, for a nanometer ultrasonic vibration, the collisionlike pressure estimated as $p_{c}\sim 10^{−4}\text{ Pa} \ll \sigma_{n}$ (~ $10\text{ Pa}$) is too small to be considered.
在这些情况下,超声波的振荡频率 $f \geq 40\text{ kHz}$ 与毫米厚颗粒层中的特征频率 $f0\sim 5\text{ kHz}$ 相比较高,因此颗粒由于惯性, 也为了承受覆盖层的重量而难以法向移动。
另一方面,对于纳米级超声波振动,类碰撞的压强所估算的 $p_{c}\sim 10^{-4}\text{ Pa} \ll \sigma_{n}$ (~ $10\text{ Pa}$) 太小,不应考虑。
In this work, we focus on the triggering of granular instabilities by small-amplitude and high-frequency sound waves. In such conditions, we have already evidenced another mechanism in which the local threshold friction force at one grain contact can be reduced by a shear acoustic lubrication, lowering the effective interparticle friction coefficient. However, the question is whether such local effects could give rise to collective motion since small-amplitude ultrasound does not induce grain displacement per se at the relevant length-scale (i.e., grain diameter $d$) during avalanches. We will show that depending on the interplay between the ultrasound amplitude and the driving force, granular layers can be found in different states: jammed solid, slow creep flow, and fast inertial liquid. Our experimental results are analyzed on the basis of velocity-weakening friction models.
在这项工作中,我们重点研究了 小振幅 和 高频 声波引发颗粒不稳定性的问题。在这种条件下,我们已经证明了另一种机制,即一个颗粒接触处的局部阈值摩擦力可以通过 剪切声学润滑 降低,从而降低等效颗粒间摩擦系数。然而,问题在于这种局部效应是否会引起集体运动,因为在雪崩过程中,小振幅超声波本身并不会在相关长度尺度(即颗粒直径 $d$)上引起颗粒位移。我们将证明,根据超声波振幅和驱动力之间的相互作用,颗粒层会出现不同的状态:堵塞固体、缓慢蠕变流动和快速惯性液体。我们根据速度减弱摩擦模型对实验结果进行了分析。
Experiments
The experimental setup is shown in Fig. 1(b). A given mass of glass beads (of diameter $d$) is deposited on the surface of an ultrasonic transducer by pluviation, building a flat and homogeneous granular layer of controlled thickness $h$ and packing density (solid volume fraction $\phi\sim 0.6$). After a waiting time of 10 min to overcome aging effects and ensure a controlled initial state, the avalanche angle $\theta = \theta_{m}$ is measured as a reference state by inclining the plane until a continuous homogeneous flow occurs (see video 1 in the Supplemental Material), for different granular layers and surface roughnesses.
实验装置如图 1(b)所示。给定质量的玻璃珠(直径为 $d$)通过冲积沉积在超声换能器表面,形成厚度为 $h$、堆积密度可控的均匀颗粒层(固体体积分数为 $\phi\sim 0.6$)。经过 $10$ 分钟的等待时间以克服老化效应并确保初始状态受控后,通过倾斜平面测量雪崩角 $\theta = \theta_{m}$,作为不同颗粒层和表面粗糙度下的参考状态,直至出现连续均匀的流动(见补充材料中的视频 1)。
The surface of the transducer (“smooth”) is used as it is, or with a controlled roughness by attaching to it, with an acoustically transparent adhesive tape, some glass beads of various diameters: $10\text{ }\mu\text{m}$ for “intermediate” and $100\text{ }\mu\text{m}$ for “rough” surfaces. We investigate granular layers composed of slightly polydisperse glass beads (about $20\%$ in size): large ($d\approx 500\text{ }\mu\text{m}$) and small ($d \approx 100\text{ }\mu\text{m}$). As reported previously, the avalanche angle depends on the thickness of the granular layer: a thicker $h$ leads to a smaller $\theta_{m}$. The avalanche angles measured for various surface roughness and layer thickness are given in Table $\text{I}$.
换能器的表面(“光滑”)按原样使用,或通过使用声学透明胶带粘贴一些不同直径的玻璃珠来控制粗糙度:$10\text{ }\mu\text{m}$ 用于 “中等” 表面,$100\text{ }\mu\text{m}$ 用于 “粗糙” 表面。我们研究了由轻微多分散的玻璃珠(大小约为 $20\%$)组成的颗粒层:大的($d\approx 500\text{ }\mu\text{m}$)和小的($d \approx 100\text{ }\mu\text{m}$)。正如之前所报告的,雪崩角取决于颗粒层的厚度:较厚的 $h$ 导致较小的 $\theta_{m}$。表 $\text{I}$ 给出了不同表面粗糙度和层厚度下测得的雪崩角。
The ultrasound vibration is delivered by transmitting a continuous sinusoidal signal to a longitudinal piezoelectric transducer at two different frequencies $f = 40$ and $100\text{ kHz}$. The input voltage varies from $10$ to $100\text{ V}$, corresponding to vibration amplitudes ranging from $U_{0}\sim 5$ to $50\text{ nm}$ calibrated with an optical interferometer. Some experiments have been conducted with shear transducers having their polarization oriented either along the slope or perpendicular to it, leading to a similar phenomenology as that reported for the longitudinal transducers.
超声波振动是通过向一个纵波压电换能器发射连续的正弦波信号来实现的,频率分别为 $f = 40$ 和 $100\text{ kHz}$。输入电压从 $10$ 到 $100\text{V}$,对应的振动幅度从 $U_{0}\sim 5$ 到 $50\text{ nm}$,用光学干涉仪校准。一些实验使用了极化方向沿斜面或垂直于斜面的剪切传感器,其结果与纵波传感器报告的现象类似。
Here, we focus on those cases where granular layers are initially jammed at an angle of inclination $\theta < \theta_{r}$. The amplitude of ultrasound is increased until the first grain motions are detected. More precisely, video of grain positions is recorded with a camera at $60$ frames/s and the trajectories and accordingly the flows of the grains are computed with a tracking procedure. The resolution of grain motions is limited by the pixel size of images that is about $5\text{ }\mu\text{m}$. The Probability Distribution Function (PDF) of grain velocities is then obtained as shown in Fig. 2 where we plot both the transverse (a) and longitudinal (along the slope) components (b).
在此,我们重点讨论颗粒层最初以倾角 $\theta < \theta_{r}$ 的方式堵塞的情况。超声波的振幅不断增大,直到检测到第一次颗粒运动。更确切地说,用摄像机以 $60$ 帧/秒的速度记录颗粒位置的视频,并通过跟踪程序计算出晶粒的运动轨迹和相应的流动情况。颗粒运动的分辨率受限于图像的像素大小,大约为 $5\text{ }\mu\text{m}$。如图 2 所示,我们绘制了横向(a)和纵向(沿斜坡)分量(b),从而得到谷物速度的概率分布函数(PDF)。
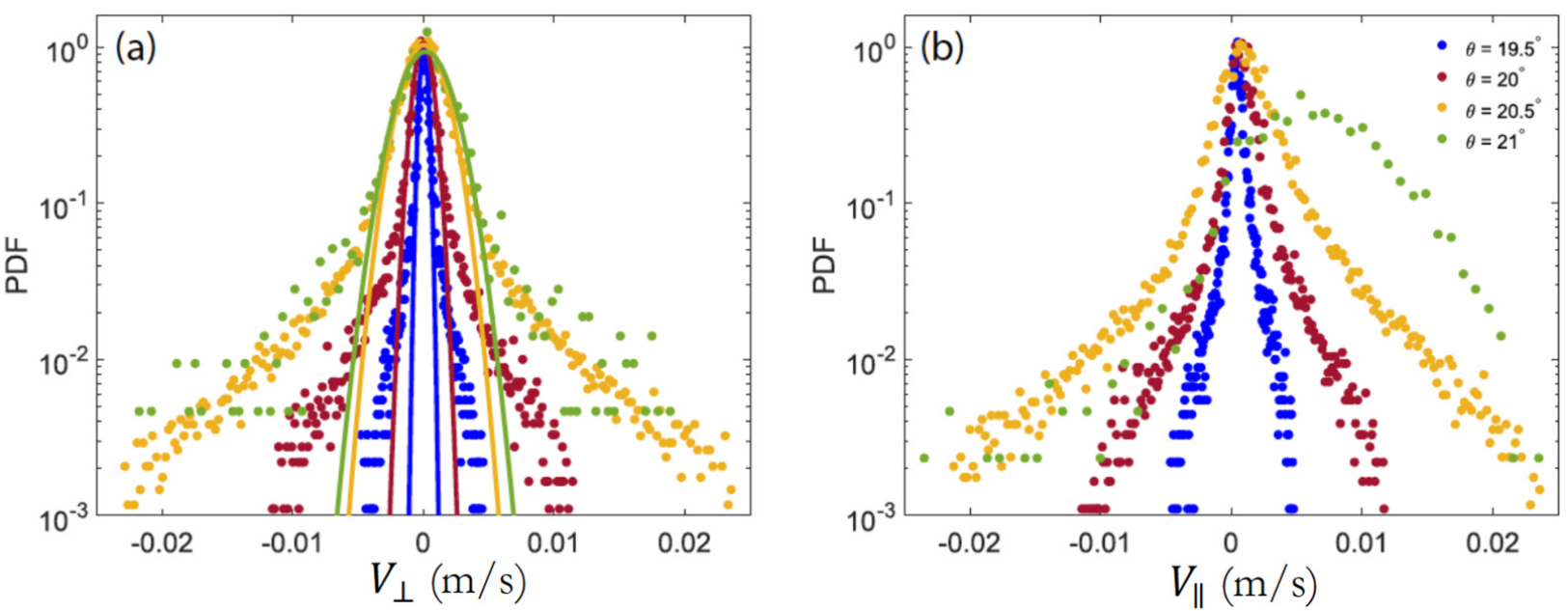
PDF of grain velocities driven by ultrasound ($U_{0} = 15\text{ nm}$) in a layer of thickness $h/d = 11.6$ ($d = 100\text{ }\mu\text{m}$) deposited on the surface of intermediate roughness. The angle of inclination $\theta$ varies from $19.5^{\circ}$ to $21^{\circ}$ ($\theta_{m} \approx 22.5^{\circ}$). (a) PDF of the transverse velocity, symmetric around $V_{\perp} = 0$. (b) PDF of the longitudinal velocity $V_{\parallel}$ along the slope, from which the average flow velocity $V_{\text{flow}}$ is computed.
沉积在中等粗糙度的表面上, 在厚度为 $h/d = 11.6$ ($d = 100\text{ }\mu\text{m}$) 的层中,由超声波($U_{0} = 15\text{ nm}$)驱动的颗粒速度 PDF. 倾斜角 $\theta$ 从 $19.5^{\circ}$ 到 $21^{\circ}$($\theta_{m} \approx 22.5^{\circ}$)。(a) 横向速度的 PDF,围绕 $V_{\perp} = 0$ 对称。 (b) 沿斜坡的纵向速度 $V_{\parallel}$ 的 PDF,由此计算出平均流速 $V_{\text{flow}}$。
The central part of the PDF is fitted with a Gaussian curve. From these PDFs, we deduce the average flow velocity $V_{\text{flow}}$ and the standard deviation $\delta V$. For the transverse component, the PDF are symmetrically distributed around $V_{\perp}$ as there is no preferential path in that direction. Along the longitu- dinal direction, the PDF are asymmetric around $V_{\parallel} = 0$ with a nonzero average flow velocity. All distributions have large tails, due to both the heterogeneous nature of the granular flow and some boundary effects due to the geometry of the transducers.
PDF 的中心部分用高斯曲线拟合。根据这些 PDF,我们可以推导出平均流速 $V_{\text{flow}}$ 和标准偏差 $\delta V$。对于横向分量,PDF 在 $V_{\perp}$ 附近对称分布,因为该方向没有优先路径。沿纵向,PDF 在 $V_{\parallel} = 0$ 附近非对称分布,平均流速不为零。所有分布都有较大的尾部,这既是由于颗粒流动的异质性,也是由于换能器的几何形状造成的一些边界效应。
Results
Dynamics of triggered granular flows
Figure 3(a) depicts the normalized friction $\mu/\mu_{S}(=\tan{\theta}/\tan{\theta_{m}})$ vs the dimensionless flow velocity $\widetilde{V} = V_{\text{flow}}/(gd)^{1/2}$ on the intermediate roughness surface. Depending on the distance to yielding, we observed different regimes of flow triggered by ultrasound. For $\mu/\mu_{S} \ll 1$ and too small amplitudes of ultrasound, the system is in the jammed state $\text{I}$, defined by the vertical (plain) line $\widetilde{V} = 0$ as in Fig. 1(d). In region $\text{II}$ close to region $\text{I}$, flow occurs at a very small averaged velocity $\widetilde{V}\sim 10^{−2}$.
图 3(a) 描述了中间粗糙度表面上归一化摩擦力 $\mu/\mu_{S}(=\tan{\theta}/\tan{\theta_{m}})$ 与无量纲流速 $\widetilde{V} = V_{\text{flow}}/(gd)^{1/2}$ 的关系。根据距离屈服的远近,我们观察到由超声引发的不同流动状态。对于 $\mu/\mu_{S} \ll 1$ 和太小的超声波振幅,系统处于 $\text{I}$ 的堵塞状态,如图 1(d)所示,由垂直(平直)线 $\widetilde{V} = 0$ 定义。在靠近 $\text{I}$ 区域的 $\text{II}$ 中,流动的平均速度非常小,为 $\widetilde{V}\sim 10^{-2}$。
Closer to yielding, for $\mu/\mu_{S}\sim 0.9$, we find a rather abrupt dynamic transition where the system jumps, around a characteristic $\widetilde{V}^{*}\sim 3 \times 10^{−2}$ (dotted line) from an intermittent creep flow to a much faster, continuous inertial flow (dashed line).
当 $\mu/\mu_{S}\sim 0.9$ 时,我们发现了一个相当突然的动态转变,在这个转变中,系统从间歇性蠕变流跃迁到更快的连续惯性流(虚线),其特征为 $\widetilde{V}^{*}\sim 3 \times 10^{-2}$(虚线)。
As shown in Fig 3(b), $\widetilde{V}^{*}$ corresponds to a marked peak in the evolution of the transverse relative velocity fluctuations $\delta V/V_{\text{flow}}$, indicating the boundary of a phase transition to the stable flow state. Above the transition, the granular layer flows with a typical $\widetilde{V} > 10^{-1}$, close to the order of magnitude of the flow velocity of a natural avalanche, which is used here arbitrarily to define region $\text{III}$ for the onset of stable flow.
如图 3(b)所示,$\widetilde{V}^{*}$ 与横向相对速度波动 $\delta V/V_{\text{flow}}$ 演变中的一个明显峰值相对应,表明了向稳定流动状态相变的边界。在过渡阶段之上,颗粒层的典型流速为 $\widetilde{V}> 10^{-1}$,接近于自然雪崩的流速数量级,这里任意用它来定义稳定流开始的区域 $\text{III}$。
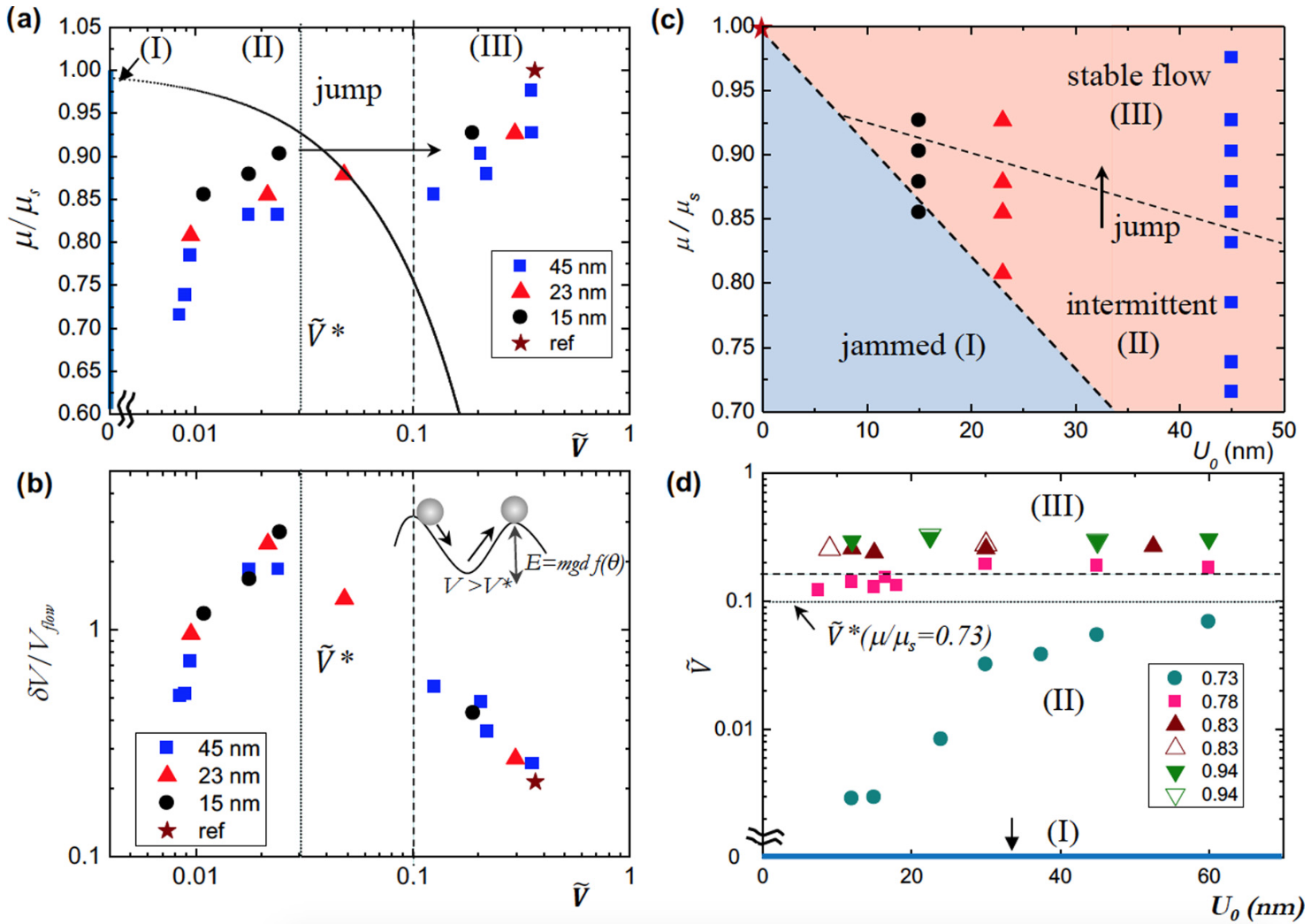
(a) Normalized friction coefficient $\mu/\mu_{S}$ vs normalized flow velocity $\widetilde{V}(=V_{\text{flow}})$ for a layer thickness $h/d = 11.6$ (with $d = 100\text{ }\mu\text{m}$) and $f = 40\text{ kHz}$ on the intermediate roughness surface ($\theta_{m} = 22.5^{\circ}$). The flow is driven by ultrasound amplitudes $U_{0} = 15$, $23$, or $45\text{ nm}$ (respectively, black circles, red triangles, and blue squares) and the symbol star corresponds to the occurrence of avalanche without ultrasound at the maximum angle $\theta_{m}$. The continuous line corresponds to the model from Ref. [17] (see text). (b) Relative transverse velocity fluctuations vs $\widetilde{V}$ . Inset illustrates the necessary initial condition $\widetilde{V} > \widetilde{V}^{*}$ for the grain to escape from a geometric trap formed by its neighbors (see text). (c) Phase diagram constructed by replotting $\mu/\mu_{S}$ from (a) as a function of $U_{0}$ illustrating different states of the system. (d) Variation of $\widetilde{V}$ vs ultrasound amplitude $U_{0}$ ( $f = 40\text{ kHz}$) at various imposed $\mu/\mu_{S}$ for a layer thickness $h_{1}/d = 3$ (with $d = 500\text{}\mu\text{m}$) on the intermediate rough surface ($\theta_{m} = 20.2^{\circ}$). The open triangles points correspond to a short-burst excitation with 1-s duration.
(a) 层厚度为 $h/d = 11.6$($d = 100\text{ }\mu\text{m}$), 中等粗糙度表面($\theta_{m} = 22.5^{\circ}$), (频率) 为 $f = 40\text{ kHz}$ 的情况下,归一化摩擦系数 $\mu/\mu_{S}$ vs 归一化流速 $\widetilde{V}(=V_{\text{flow}})$。流动由超声波振幅 $U_{0}=15$、$23$ 或 $45\text{ nm}$(分别为黑色圆圈、红色三角形和蓝色正方形)驱动,符号星代表在最大角度 $\theta_{m}$ 时未施加超声波而发生雪崩。连续线对应于参考文献 [17] 中的模型(见正文)。 (b) 相对横波速度涨落 vs $\widetilde{V}$。 插图说明了必要的初始条件 $\widetilde{V} > \widetilde{V}^{*}$ 才能使颗粒逃离由其近邻形成的几何陷阱(见正文)。 (c) 将 (a) 中的 $\mu/\mu_{S}$ 作为 $U_{0}$ 的函数重新绘制的相图,说明了系统的不同状态。 (d) 在中等粗糙表面($\theta_{m} = 20.2^{\circ}$)上,层厚度为 $h_{1}/d = 3$($d = 500\text{}\mu\text{m}$)时,不同施加 $\mu/\mu_{S}$ 条件下,$\widetilde{V}$与超声波振幅 $U_{0}$($f = 40\text{kHz}$)的变化。$\Delta$ 对应于持续时间为 1 秒的短脉冲激励。
The observed ultrasound-induced granular flow may be characterized by different states as provided by the order of magnitude of the typical average velocity. This is shown in Fig. 3(c) where $\mu/\mu_{S}$ is replotted from Fig. 3(a) but as a function of the ultrasound amplitude $U_{0}$. Such a phase diagram shows that transition between the jammed state, the creep flow state, and stable flow state shall occur via arbitrary paths in the $(\mu, U_{0})$ plane. Below, we shall suggest a local friction model to describe the line schematically delimiting jammed state $\text{I}$ and flowing state $\text{I/II}$.
观察到的超声波诱导的颗粒流可以根据典型平均速度的数量级来特征不同的状态。如图 3(c) 所示,图 3(a) 中的 $\mu/\mu_{S}$ 是超声振幅 $U_{0}$ 的函数。这样的相图表明,在堵塞状态、蠕变流动状态和稳定流动状态之间的过渡将通过 $(\mu, U_{0})$ 平面上的任意路径发生。下面,我们将提出一个局部摩擦模型,来描述堵塞状态 $\text{I}$ 和流动状态 $\text{I/II}$ 的分界线。
Moreover, inspection of Fig. 3(a) suggests that in the dynamic transition zone between regions $\text{II}$ and $\text{III}$, the flow velocity is an increasing function of the amplitude at imposed shear $\mu$. For example, for $\mu/\mu_{S}\approx 0.85$, when the ultrasound amplitude $U_{0}$ is increased from $15$ to $45\text{ nm}$, the flow velocity is increased by $\Delta V_{\text{flow}}\approx 3\text{ mm/s}$, which gives an increasing factor about $V_{\text{flow}}/U_{0}\sim 10^{5}\text{ s}^{−1}$.
此外,图 3(a) 显示,在 $\text{II}$ 和 $\text{III}$ 区域之间的动态过渡区,流速是施加剪切力 $\mu$ 时振幅的递增函数。例如,对于 $\mu/\mu_{S}\approx 0.85$,当超声振幅 $U_{0}$ 从 $15$ 增加到 $45\text{ nm}$ 时,流速增加了 $\Delta V_{\text{flow}}\approx 3\text{ mm/s}$,这给出了约 $V_{\text{flow}}/U_{0}\sim 10^{5}\text{ s}^{-1}$ 的增大因子。
We confirm this trend with more precision by showing additional measurements of $\widetilde{V}$ from experiments achieved with a fine increase of the ultrasound amplitude at constant inclination in a layer of large beads $d = 500\text{}\mu\text{m}$ as shown by Fig. 3(d). At $\mu/\mu_{S} = 0.73$, the flow velocity increases continuously with amplitude $U_{0} > 25\text{ nm}$, such that $V_{\text{flow}}/U_{0} = 1.1 \times 10^{5}\text{ s}^{−1}$, a value consistent with the preceding measurement. In this region ($\text{II}$) where the flow velocity is controlled by ultrasound, the granular layer stops flowing when the ultrasound is removed (see video 2 in the Supplemental Material).
如图 3(d) 所示,我们通过在大球珠层 $d = 500\text{}\mu\text{m}$ 中以恒定倾角细微增加超声波振幅的实验,对 $\widetilde{V}$ 进行了额外测量,从而更精确地证实了这一趋势。当 $\mu/\mu_{S} = 0.73$ 时,流速随振幅 $U_{0} > 25\text{ nm}$ 的增大而持续增加。,这样 $V_{\text{flow}}/U_{0} = 1.1 \times 10^{5}\text{ s}^{-1}$,这个值与前面的测量结果一致。在这个由超声波控制流速的区域($\text{II}$),当超声波被移除时,颗粒层会停止流动(见补充材料中的视频 2)。
By contrast, as shown in Fig. 3(a), when the inclination increased close to the threshold at $\mu/\mu_{S}\ll 1$, the dynamics of flow converges toward the reference state (marked by the star symbols), i.e., the onset of avalanche without ultrasound, in region $\text{{III}}$ [Fig. 3(d)]. There, the inertial flow at a typical velocity $\widetilde{V}\geq 1.5\times 10^{-1}$, used to define region $\text{III}$ (dashed line), is mostly insensitive to ultrasound, being only a function of the imposed shear $\mu$ as confirmed, e.g., for $\mu/\mu_{S} = 0.83$.
相比之下,如图 3(a)所示,当倾角增加到接近 $\mu/\mu_{S}\ll 1$ 的阈值时,流的动态趋近于参考状态(星号标记),即在 $\text{III}$ 区域未施加超声波的雪崩开始[图 3(d)]。在那里,惯性流的典型速度为 $\widetilde{V}\geq 1.5\times 10^{-1}$,用于定义 $\text{III}$ 区域(虚线),并且在大部分情况下对超声波不敏感,仅是外加剪切力 $\mu$ 的函数,例如,在 $\mu/\mu_{S} = 0.83$ 时已得到证实。
We found additionally that in region $\text{III}$, applying the ultrasound either by a short burst (of 1-s duration) or by a continuous wave results in the same flow velocity. All our experiments show that close to $\mu_{S}$, ultrasound vibrations only affect the threshold but not the flow dynamics.
我们还发现,在 $\text{III}$ 区域,无论是短脉冲(持续时间为 1 秒)还是连续波,超声波都会导致相同的流速。我们的所有实验都表明,在接近 $\mu_{S}$ 的地方,超声波振动只会影响阈值,而不会影响流动力学。
Unjamming by ultrasound
In Fig. 4, we investigate in more details the unjamming by ultrasound of static layers of large beads ($d = 500\text{ }\mu\text{m}$) at $\mu_{S}^{*}(U_{0})$ from the jammed state ($\text{I}$). This threshold $\mu_{S}^{*}$ decreases linearly with increasing $U_{0}$ in a systematic manner as for the $\text{I}-\text{II}$/$\text{III}$ line in Fig. 3(c), which confirms that perturbations by ultrasound excitation and static shear stress play complementary roles in the triggering process.
在图 4 中,我们更详细地研究了在 $\mu_{S}^{*}(U_{0})$ 时,超声波对大颗粒静态层($d = 500\text{ }\mu\text{m}$ )的解堵塞作用,即从堵塞状态($\text{I}$)开始。这个阈值 $\mu_{S}^{*}$ 随着 $U_{0}$ 的增加而线性降低,就像图 3(c) 中的 $\text{I}-\text{II}$/$\text{III}$ 线一样,这证实了超声激励和静态剪切应力的扰动在触发过程中起到了互补作用。
Figures 4(a) and 4(b) show that the unjamming starts at smaller amplitude for low frequency of vibration, low roughness of the transducer, and small thickness of the granular layer. When the unjamming occurs, large flow velocities were found for $\mu$ close to $\mu_{S}$, as those observed in Fig. 3(d).
图 4(a)和 4(b) 显示,在振动频率低、传感器粗糙度低和颗粒层厚度小的情况下,解卡开始于较小的振幅。当发生解堵塞时,发现 $\mu$ 接近 $\mu_{S}$ 时流速较大,如图 3(d) 中观察到的那样。
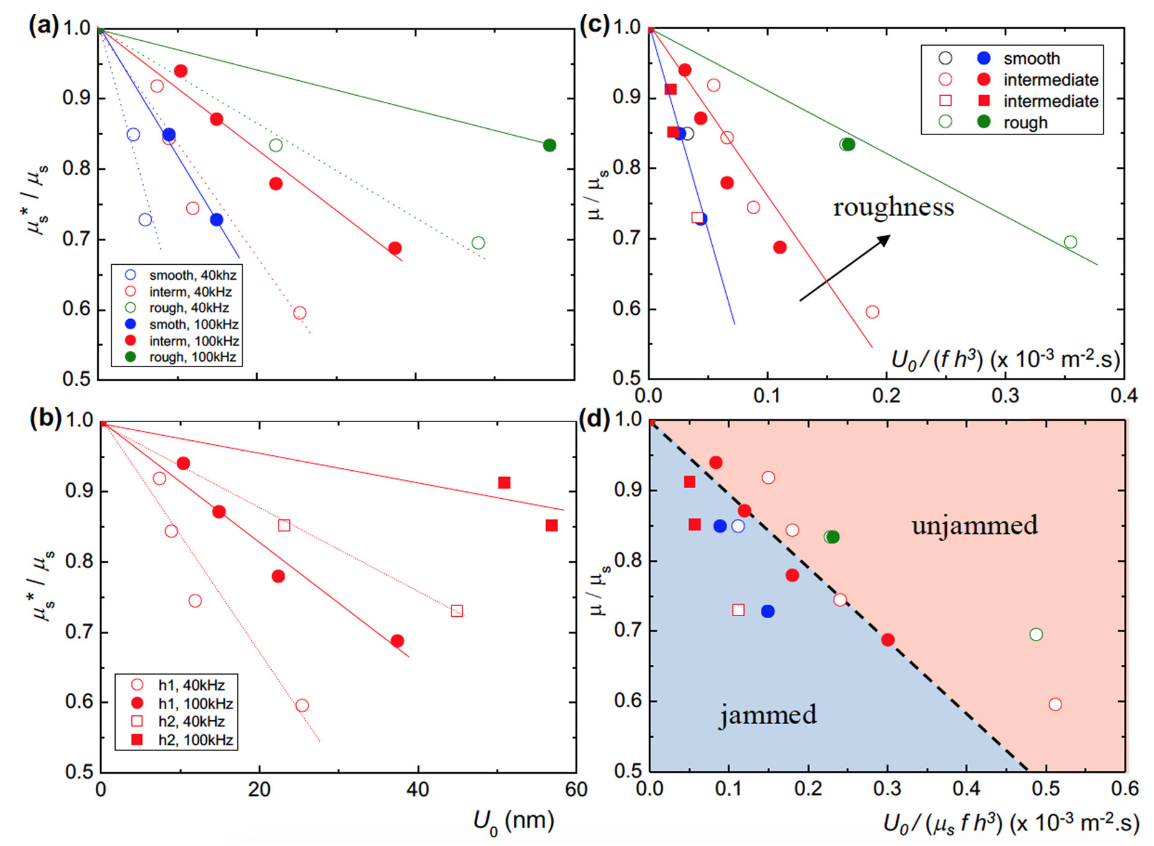
(a) Variation of the normalized static friction coefficient (threshold) $\mu_{S}^{*}/\mu_{S}$ vs ultrasound amplitude $U_{0}$, for the granular layer with thickness $h_{1}/d = 3 (d = 500\text{ }\mu\text{m})$. Blue, red, and green symbols correspond to the smooth, intermediate, and rough surfaces, respectively. Open (filled) symbols correspond to $f = 40\text{ kHz}$ ($100\text{ kHz}$). Lines are fits to the data with Eq. $\eqref{eq3}$. (b) Normalized friction coefficient for two layers of different thicknesses, $h_{1}/d = 3$ [same symbols as in (a)] and $h_{2}/d = 6$ (square points). The surface is of intermediate roughness and the measurements are achieved either at $40$ or $100\text{ kHz}$ [same as in (a)]. (c) Data from (a) and (b) plotted against the rescaled amplitude $U_{0}/( f h^{3})$, emphasizing the role of surface roughness. (d) All data rescaled by Eq. $\eqref{eq3}$, showing the jammed and unjammed states from either side of the $\mu_{S}^{*}$ line, equivalent to the $\text{I}-\text{II}$/$\text{III}$ line in Fig 3(c).
(a) 厚度为 $h_{1}/d = 3 (d = 500\text{ }\mu\text{m})$ 的颗粒层的归一化静摩擦系数(阈值)$\mu_{S}^{*}/\mu_{S}$ 与超声振幅 $U_{0}$ 的变化。蓝色、红色和绿色符号分别对应光滑表面、中等粗糙表面和粗糙表面。空心(填充)符号对应 $f = 40\text{ kHz}$ ($100\text{ kHz}$)。直线是用公式 $\eqref{eq3}$ 对数据进行的拟合。 (b) 两层不同厚度的归一化摩擦系数,$h_{1}/d = 3$ [符号与 (a) 中相同] 和 $h_{2}/d = 6$(方形点)。表面为中等粗糙度,测量频率为 $40$ 或 $100\text{ kHz}$ [与 (a) 中相同]。 (c) (a)和(b)中的数据与重标定振幅 $U_{0}/( f h^{3})$ 的关系图,强调了表面粗糙度的作用。 (d) 按公式 $\eqref{eq3}$ 重标的所有数据,显示了 $\mu_{S}^{*}$ 线两侧的堵塞态和非堵塞态,相当于图 3(c) 中的 $\text{I}-\text{II}$/$\text{III}$ 线。
Discussion
Bifurcation between creeplike flow and self-accelerated inertial flow (macroscopic-scale analysis)
To understand qualitatively the different regimes of flow triggered by ultrasound (Fig. 3), we use as a guide the heuristic friction model developed by Jaeger et al.:
$$ \mu = \mu_{S}/(1 + \alpha_{1}\widetilde{\dot{\gamma}}^{2}) + \beta\widetilde{\dot{\gamma}}^{2}.\tag{1}\label{eq1} $$
Here, $\mu(\dot{\gamma})$ is the normalized shear defined above, $\widetilde{\dot{\gamma}} = \dot{\gamma}\sqrt{d/g_{\perp}}$ ($d$ is the grain size) is the dimensionless flow (shear) rate with $g_{\perp} = g\cos{\theta}$ and $\dot{\gamma}$ would scale with $V_{\text{flow}}/h$ ($h$ is related to the sample thickness).
为了定性地理解超声波引发的不同流动状态(图 3),我们使用了 Jaeger 等人开发的启发式摩擦模型作为指导:
$$ \mu = \mu_{S}/(1 + \alpha_{1}\widetilde{\dot{\gamma}}^{2}) + \beta\widetilde{\dot{\gamma}}^{2}. $$
这里,$\mu(\dot{\gamma})$ 是上面定义的归一化剪切力, $\widetilde{\dot{\gamma}} = \dot{\gamma}\sqrt{d/g_{perp}}$($d$为颗粒尺寸)是无量纲流动(剪切)速率,其中 $g_{\perp} = g\cos{\theta}$ 和 $\dot{\gamma}$ 使用 $V_{\text{flow}}/h$($h$与样品厚度有关)标定。
$\mu_{S}$ is the granular static friction coefficient, which depends on the grain-grain friction as well as on the depth of the trapping by neighboring grains in the limit $\widetilde{\dot{\gamma}}\rightarrow 0$. $\alpha_{1}$ and $\beta$ describe the geometry of the particles and the energy loss during collisions, which involves the coefficient of restitution.
Figure 5(a) shows a typical plot of $\mu(\dot{\gamma})$ calculated from Eq. $\eqref{eq1}$ using the parameters as in Ref. [16] where a metastable region is found for $\mu_{d}(\widetilde{\dot{\gamma}}_{0} < \mu < \mu_{S})$ corresponding to the negative slope for $0 < \widetilde{\dot{\gamma}} < \widetilde{\dot{\gamma}}_{0}$, as shown by Fig. 1(d).
$\mu_{S}$ 是颗粒静摩擦系数,它取决于颗粒与颗粒之间的摩擦力以及在极限 $\widetilde{\dot{\gamma}}\rightarrow 0$ 条件下近邻颗粒的捕获深度。$\alpha_{1}$ 和 $\beta$ 描述了颗粒的几何形状以及碰撞过程中的能量损失,这涉及到恢复系数。
图 5(a) 显示了根据公式 $\eqref{eq1}$ 计算出的 $\mu(\dot{\gamma})$ 的典型图,使用的参数与参考文献[16]相同; 其中的 $\mu_{d}(\widetilde{\dot{\gamma}}_{0} < \mu < \mu_{S})$ 对应于负斜率的 $0 < \widetilde{\dot{\gamma}} < \widetilde{\dot{\gamma}}_{0}$,由此发现了一个亚稳态区域, 如图 1(d) 所示。
In such a case, as proposed there, the unlimited flow is possible only when the initial flow rate or velocity is larger than $\dot{\gamma}^{*}$ or $V^{*}$ (see also discussion below) given by the velocity-weakening part of $\mu(\dot{\gamma})$ as we likely observed in the jump region of Fig. 3(a). This velocity-weakening regime can initiate the stick-slip frequently observed in solid friction and granular media, due to aging-rejuvenation competition acting at contact asperities.
在这种情况下,正如我们在图 3(a)的跃迁区域所观察到的那样,只有当初始流速或速度大于 $\dot{\gamma}^{*}$ 或 $V^{*}$(另见下文讨论),由 $\mu(\dot{\gamma})$ 的速度减弱部分给出时,无限流动才有可能发生。这种速度减弱机制可以引发在固体摩擦和颗粒介质中经常观察到的粘滞滑动,这是由于老化-恢复竞争作用于接触表面所致。
In solid friction, this leads to the bifurcation between creep motion and self-accelerated slip at a multicontact interface via an increasing oscillating shear force close to the yielding. In granular media, we may expect a similar aging-rejuvenation competition in which contact asperities are replaced by grain contacts. Depending on the imposed shear $\mu$ relative to the static threshold $\mu_{S}$ and the initial shear rate $\widetilde{\dot{\gamma}}$ , the granular dynamics could bifurcate between a self-accelerated flow (avalanche in region $\text{III}$) and a creep which stops to flow at long time range and recovers the static state (in region $\text{I}$).
在固体摩擦中,这将导致蠕变运动和多接触界面上的自加速滑移之间的分叉,并通过接近屈服的不断增加的振荡剪切力来实现。在颗粒介质中,我们可能会遇到类似的老化-再生竞争,其中接触表面被晶粒接触所取代。根据相对于静态阈值 $\mu_{S}$ 和初始剪切速率 $\widetilde{\dot{\gamma}}$ 的外加剪切力 $\mu$,颗粒动力学会在自加速流动(区域 $\text{III}$ 中的雪崩)和蠕变(在较长的时间范围内停止流动并恢复静态(区域 $\text{I}$ 中))之间分叉。
Let us now consider the effect of ultrasound for these two different flows in granular layers. As reported in Ref. [12], the ultrasonic vibration can induce the frictional slip between grain contacts, leading to the frictional dissipation, the softening of the shear contact stiffness, and accordingly of the macroscopic modulus in a granular medium.
Moreover, we have shown in the configuration of a single sphere-plane contact that such oscillation-induced frictional slip can also lubricate acoustically the contact, leading to the reduction of the static threshold from $\mu_{S}$ to $\mu_{S}^{*}$ (see discussion below).
现在让我们来看看超声波对颗粒层中这两种不同流动的影响。正如文献[12]所报道的,超声波振动可诱导晶粒接触间的摩擦滑移,导致摩擦耗散。文献[12]指出,超声波振动可诱发颗粒接触间的摩擦滑移,从而导致摩擦耗散、剪切接触刚度软化以及颗粒介质中的宏观模量相应减小。
此外,我们已经在单个球面-平面接触的构造中证明,这种振荡引起的摩擦滑移也可以使接触产生声学润滑,从而使静态阈值从 $\mu_{S}$ 降至 $\mu_{S}^{*}$ (见下文讨论)。
Such a decrease of the threshold modifies the above friction model as shown in Fig. 5(a) where the reference blue curve, corresponding to $\mu_{S}$, is lowered to the pink one with $\mu_{S}^{*} < \mu_{S}$. The avalanche is then triggered by ultrasound whenever the granular is loaded such that $\mu > \mu_{S}^{*}$—the main observation of this work.
More specially, we propose the scenario as follows for two different imposed shear: close to the threshold such that $\mu = \mu_{1}$ with $\mu_{d}(\widetilde{\dot{\gamma}}_{0}) < \mu_{1} \leq \mu_{S}$, and far below the threshold with $\mu = \mu_{2} < \mu_{d}$ .
如图 5(a) 所示,阈值的降低改变了上述摩擦模型,其中与 $\mu_{S}$ 相对应的蓝色参考曲线降低为粉红色,$\mu_{S}^{*} < \mu_{S}$. 每当颗粒被加载到 $\mu > \mu_{S}^{*}$ 时,超声波就会触发雪崩–这是本研究的主要观察结果。
更具体地说,我们针对两种不同的外加剪切力提出了如下方案:接近阈值时,$\mu = \mu_{1}$,$\mu_{d}(\widetilde{\dot{\gamma}}_{0}) < \mu_{1}$;远低于阈值时,$\mu = \mu_{2} < \mu_{d}$.
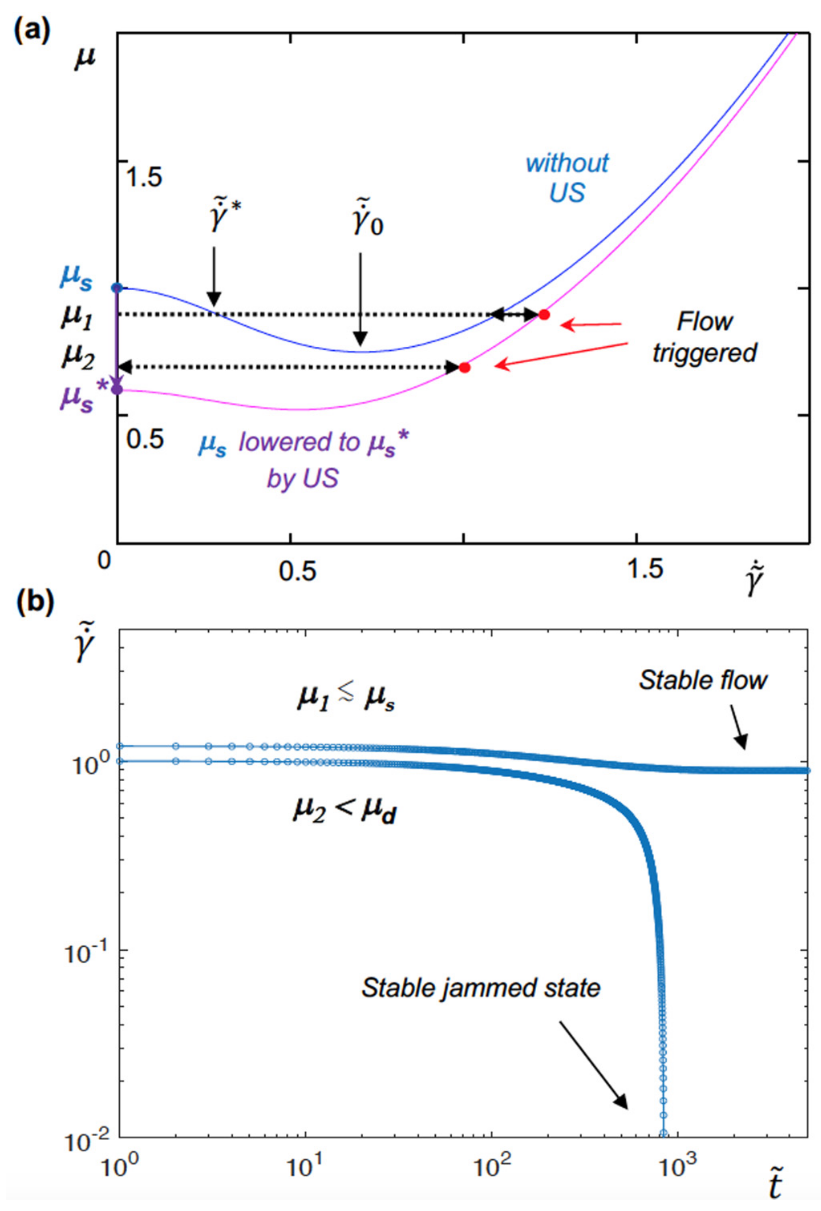
(a) Effective friction coefficient $\mu$ versus flow rate $\widetilde{\dot{\gamma}}$ derived from Eq. $\eqref{eq1}$ (blue curve) with $\alpha_{1} = 2$, $\beta = 0.5$, and $\mu_{S} = 1$ as in Ref. [16], which depicts the velocity-weakening behavior for $0 < \widetilde{\dot{\gamma}} < \widetilde{\dot{\gamma}}$. The minimum shear is $\mu_{d} = 0.75$ at $\widetilde{\dot{\gamma}}_{0} = 0.7$. The application of ultrasound reduces the interparticle friction coefficient, thus lowering the avalanche angle or yield stress from $\mu_{S} = 1$ (blue curve) to $\mu_{S}^{*} = 0.6$ (pink curve). This triggers the granular flow (red points) as explained in the text. (b) Evolution of the flow rate as a function of time after the removal of ultrasound. The triggered flow bifurcates between a stable inertial flow for imposed shear $\mu_{1} = 0.9\leq\mu_{S}$ (with $\widetilde{\dot{\gamma}}_{i} = 1.2$) and a jamming creep regime for imposed shear $\mu_{2} = 0.7 < \mu_{d}$ (with $\widetilde{\dot{\gamma}}_{i} = 1.0$) (see text).
For $\mu_{1}\leq \mu_{S}$, the flow is triggered from the metastable state and persists when the ultrasound is turned off since the $\tau - \dot{\gamma}$ relation recovers to the initial curve (blue). Indeed, the system is now driven to the inertial flow region ($\text{III}$), dominated by the term $\beta\widetilde{\dot{\gamma}}^{2}$ in Eq. $\eqref{eq1}$, where the static coefficient of friction $\mu_{S}$ and hence the ultrasound-induced decrease $\mu_{S}^{*}$ are expected to have a vanishing effect.
This corresponds precisely to our experimental observations in Fig. 3(d) for $\mu_{1} > 0.76$, where the data obtained with either the short burst or the continuous ultrasonic excitation are indistinguishable.
对于 $\mu_{1}\leq \mu_{S}$,由于 $\tau - \dot{\gamma}$ 关系恢复到初始曲线(蓝色),因此流动从亚稳态被触发,并在解除超声波后持续存在。事实上,系统现在被驱动到了惯性流区域($\text{III}$),由公式 $\eqref{eq1}$ 中的项 $\beta\widetilde{\dot{\gamma}}^{2}$ 主导,其中静摩擦系数 $\mu_{S}$ 以及超声波引起的下降 $\mu_{S}^{*}$ 预期会产生逐渐消失的影响。
这与图 3(d) 中 $\mu_{1} > 0.76$ 时的实验结果完全吻合,此时短脉冲串或连续超声波激励所获得的数据是无法分辨的。
By contrast, for imposed shear $\mu_{2} < \mu_{d}$ (minimum value in the blue curve) the granular system stops to flow in the absence of ultrasound and goes back to the initial solution at $\widetilde{\dot{\gamma}}$, i.e., the stable jammed state ($\text{I}$). Moreover, in the latter case, the velocity of triggered flow increases with increasing ultrasound amplitude by lowering further $\mu_{S}$, as for the experimental observa- tion in Fig. 3(d) with $\mu = 0.73$.
相比之下,当施加的剪切力 $\mu_{2}< \mu_{d}$(蓝色曲线中的最小值)时,颗粒系统在未施加超声波的情况下停止流动,回到 $\widetilde{\dot{\gamma}}$ 处的初始解,即稳定的堵塞状态($\text{I}$)。此外,在后一种情况下,通过进一步降低 $\mu_{S}$,被诱发的(颗粒)流的速度会随着超声波振幅的增加而增加,如图 3(d) 中 $\mu = 0.73$ 的实验观察结果。
We may also investigate this bifurcation phenomenon from the given initial condition to the stable states as a function of time. To do so, we consider the motion of a single mass (“slider”) on an inclined plane [inset of Fig. 1(b)] within the framework of a mean-field approximation. It is submitted to a shear force by gravity and a friction by the phenomenological friction law in Eq. $\eqref{eq1}$.
我们还可以研究从给定初始条件到稳定状态随时间变化的分叉现象。为此,我们在平均场近似的框架内考虑单个质量(“滑块”)在倾斜平面上的运动[图 1(b) 插图]。它受到重力的剪切力和公式 $\eqref{eq1}$ 中现象摩擦定律的摩擦力。
The mean acceleration approximately written as $\mathrm{d}\langle V\rangle/\mathrm{d}t$ with $\langle V\rangle\sim V_{\text{flow}}$ (denoted as $V$ below for simplicity) is given by [16,17]: $m(\mathrm{d}V/\mathrm{d}t) = F_{t} − \mu F_{n}$ where the shear force $F_{t} = mg \sin{\theta}$ is imposed by the inclined plane, $F_{n} = mg \cos{\theta}$ and the friction coefficient $\mu$ given by Eq. $\eqref{eq1}$. Using the dimensionless unit $\widetilde{t} = t/\sqrt{d/g_{\perp}}$, we write the equation of motion as
$$ \mathrm{d}\widetilde{\dot{\gamma}}/\mathrm{d}\widetilde{t} = \tan{\theta} - \mu_{S}/(1 + \alpha_{1}\widetilde{\dot{\gamma}}^{2}) - \beta\widetilde{\dot{\gamma}}^{2}.\tag{2}\label{eq2} $$
平均加速度近似地写成 $\mathrm{d}\langle V\rangle/\mathrm{d}t$ ,其中 $\langle V\rangle\sim V_{\text{flow}}$(为简单起见,以下用 $V$ 表示),其值由文献 [16,17] 给出: $m(\mathrm{d}V/\mathrm{d}t) = F_{t}- \mu F_{n}$ 其中剪切力 $F_{t} = mg \sin{\theta}$ 是由斜面施加的,$F_{n} = mg \cos{\theta}$ 和摩擦系数 $\mu$ 由公式 $\eqref{eq1}$ 给出。使用无量纲单位 $\widetilde{t} = t/\sqrt{d/g_{\perp}}$,我们可以把运动方程写成
$$ \mathrm{d}\widetilde{\dot{\gamma}}/\mathrm{d}\widetilde{t} = \tan{\theta} - \mu_{S}/(1 + \alpha_{1}\widetilde{\dot{\gamma}}^{2}) - \beta\widetilde{\dot{\gamma}}^{2}. $$
Figure 5(b) depicts the solutions of the flow velocity as a function of time, calculated from Eq. $\eqref{eq2}$ with the $\color{red}{\text{i}}$nitial flow rates $\widetilde{\dot{\gamma}}_{\color{red}{i}}$ corresponding to the triggered flows under two imposed shears [red circles in Fig. 5(a)], $\mu_{1} = \tan{\theta_{1}}$ with $\widetilde{\dot{\gamma}}_{i} = 1.2$ and $\mu_{2} = \tan{\theta_{2}}$ with $\widetilde{\dot{\gamma}}_{i} = 1$, respectively. For the inclined plane at $\theta_{1}$, the system reaches a steady inertial flow at long time whereas for the lower inclination $\theta_{2}$, the flow slows down and arrests quickly, being consistent with the above analysis via Fig. 5(a).
图 5(b) 描述了根据公式 $\eqref{eq2}$ 计算出的流速随时间变化的解,其初始流速为 $\widetilde{\dot{\gamma}}_{i}$ ,对应于两个外加剪切力下的被诱发(颗粒)流[图 5(a) 中的红圈], $\mu_{1} = \tan{\theta_{1}}$,其中 $\widetilde{\dot{\gamma}}_{i} = 1.2$;以及 $\mu_{2} = \tan{\theta_{2}}$,其中 $\widetilde{\dot{\gamma}}_{i} = 1$。对于倾角为 $\theta_{1}$ 的倾斜面,系统在较长时间内达到稳定的惯性流动,而对于倾角为 $\theta_{2}$ 的倾斜面,流动速度减慢并迅速停滞,这与上述图 5(a) 的分析一致。
Qualitatively, such a bifurcation agrees well with our experiments on triggered granular flows [Figs. 3(c) and 3(d)]. It is worth noting that in yield stress fluids such as foams, emulsions, and polymers the thixotropic effect resulting from the competition between structuration and destruction by shear can also lead to a viscosity bifurcation as a function of time.
从性质上讲,这种分叉与我们的触发颗粒流实验[图 3(c) 和 3(d)]非常吻合。值得注意的是,在屈服应力流体(如泡沫、乳液和聚合物)中,剪切力造成的结构化和破坏之间的竞争所产生的触变效应也会导致粘度随时间发生分叉。
From creep to inertial granular flows (local-scale analysis)
Simulations and experiments showed that in the quasistatic regime at a very low imposed flow velocity, external driving induces large velocity fluctuations of grains when the system is far below the yield stress, associated with the complex dynamics of a grain confined by high local static threshold. However, at high flow velocity, the relative velocity fluctuations decrease with the flow velocity.
Here, Fig. 3(b) shows that all data collapse on the same curve when plotting the relative transverse velocity fluctuations $\delta V/V_{\text{flow}}$ versus flow velocity, independent of the ultrasound amplitude and of the inclination.
模拟和实验结果表明,在施加流速很低的准静态条件下,当系统远低于屈服应力时,外部驱动会导致颗粒产生较大的速度波动,这与高局部静态阈值导致的颗粒复杂动力学有关。然而,在高流速下,相对速度波动随流速降低而减小。
图 3(b) 显示,在绘制相对横向速度波动 $\delta V/V_{\text{flow}}$ 与流速的关系曲线时,所有数据都收敛在同一条曲线上,与超声振幅和倾角无关。
Around a threshold flowing velocity $\widetilde{V}^{*}\sim 0.03$, the relative velocity fluctuations $\delta V/V_{\text{flow}}$ abruptly becomes a decreasing function of $V_{\text{flow}}$ (or $\widetilde{V}$ ) similar to previous studies.
Above $\widetilde{V}^{*}$, the observed small relative velocity fluctuations are characteristic of the large failure event dominated by the inertial number: the granular layer is in the inertial flow state (region $\text{III}$), corresponding to highly uncorrelated grain motion.
在临界流速 $\widetilde{V}^{*}\sim 0.03$ 附近,相对速度波动 $\delta V/V_{\text{flow}}$ 突然成为 $V_{\text{flow}}$(或 $\widetilde{V}$ )的递减函数,这与之前的研究类似。
在 $\widetilde{V}^{*}$ 以上,观察到的小的相对速度波动是由惯性数主导的大破坏事件的特征:颗粒层处于惯性流状态(区域 $\text{III}$),对应于高度不相关的颗粒运动。
There, the dynamics arising from the naturally occurring avalanche at $\mu_{S}$ and the triggered flows are indistinguishable [Fig. 3(b)], which is consistent with the observation in Fig. 3(a) where the effect of ultrasound is negligible during the fast continuous flow. This is also in line with the results in Fig. 3(d) close to $\mu_{S}$ where triggered avalanches flow at the same velocity with or without prolonged ultrasound.
在那里,$\mu_{S}$ 处自然发生的雪崩和诱发(颗粒)流产生的动力学是无法区分的[图 3(b)],这与图 3(a)中的观测结果一致,即在快速连续流中超声波的影响可以忽略不计。这也与图 3(d) 中接近 $\mu_{S}$ 的结果一致,在那里,无论有没有长时间的超声波,触发的雪崩都以相同的速度流动。
Below $\widetilde{V}^{*}$, for $\mu/\mu_{S}\ll 1$, perturbations such as shear and vibration can induce some grain motion but the momentum transfer is insufficient for a global flow (avalanche), given the low static load.
In the intermittent regime for an imposed shear load near the metastable zone, the averaged creep flow induced by ultrasound increases with the vibration amplitude, as shown in Fig. 3(d) for $\mu/\mu_{S} = 0.73$. This is probably due to the decrease of the interparticle friction coefficient $\mu_{g}$ induced by the acoustic lubrication which ensures a decreased frictional loss during local slipping events.
在 $\widetilde{V}^{*}$ 以下,对于 $\mu/\mu_{S}\ll 1$,剪切和振动等扰动会诱发一些颗粒运动,但由于静载荷较低,动量传递不足以产生全局流动(雪崩)。
如图 3(d) 中 $\mu/\mu_{S} = 0.73$ 所示,在亚稳态区附近施加剪切载荷的间歇体系中,超声诱导的平均蠕变流随振动振幅的增加而增加。这可能是由于声学润滑导致颗粒间摩擦系数 $\mu_{g}$ 下降,从而确保在局部滑动事件中摩擦损耗减少。
The robust superposition of the relative velocity fluctuations in Fig. 3(b) suggests that the order of magnitude of the threshold velocity $V^{*}$ is given by the intrinsic dynamics of the granular system. The intensity of the threshold velocity results from the kinetic energy acquired by the grains during the ultrasound-induced rearrangement events, and should be large enough for the grains not to remain trapped after collisions.
Then, one needs $(1/2)mV^{* 2} = E (\theta) = mg d f (\theta)$ if the shocks are elastic [see inset of Fig. 3(b)] with $f(\theta)\sim [1 − \cos(\theta − \theta_{m} )]\sim (\theta − \theta_{m})^{2}/2$, corresponding to a geometric parameter. This gives a minimum velocity $V(\mu)\geq V^{*} = (\mu_{S} − \mu)(gd)^{1/2}$ for escaping the potential energy trap near the threshold.
图 3(b) 中相对速度波动的稳健叠加表明,阈值速度 $V^{*}$ 的数量级由颗粒系统的内在动力学给出。阈值速度的强度来自于颗粒在超声波诱导的重排事件中获得的动能,其大小应足以使颗粒在碰撞后不会继续被困住。
然后,如果冲击是弹性的,我们需要 $(1/2)mV^{* 2} = E (\theta) = mg d f (\theta)$ [见图 3(b) 的插页],其中 $f(\theta)\sim [1 - \cos(\theta - \theta_{m} )]\sim (\theta-\theta_{m})^{2}/2$,对应于一个几何参数。这给出了逃逸阈值附近的阱的最小速度 $V(\mu)\geq V^{*} = (\mu_{S} - \mu)(gd)^{1/2}$ 。
As shown Fig. 3(a) this order of magnitude for the threshold velocity $\widetilde{V}^{*}\sim \mu_{S} - \mu\sim 0.04$ (with $\mu_{S} = \tan{\theta_{m}} \approx 0.41$) corresponds consistently to the location of the velocity jump $\widetilde{V}^{*}$(~ $0.03$) observed in the curves $\mu(\widetilde{V})$ at imposed shear around $\mu/\mu_{S}\sim 0.9$ and define a transitional boundary separating conveniently region $\text{II}$, where the flow velocity depends on the amplitude, from the inertial flow region $\text{III}$.
如图3(a)所示,阈值速度 $\widetilde{V}^{*}$ 的数量级约为 $\mu_{S} - \mu$ 的数量级,大约为 $0.04$(其中 $\mu_{S} = \tan{\theta_{m}} \approx 0.41$)。这一阈值速度一致对应于在施加的剪切为 $\mu/\mu_{S}\approx 0.9$ 时,在曲线 $\mu(\widetilde{V})$ 中观察到的速度跃迁 $\widetilde{V}^{*}$(约为 $0.03$)的位置,并定义了一个过渡边界,方便地将依赖于振幅的流动速度的区域 $\text{II}$ 与惯性流动区域 $\text{III}$ 分隔开。
We may also estimate the characteristic velocity for the system with larger beads in Fig. 3(d) at $\mu/\mu_{S} = 0.73$ (region $\text{II}$), $\widetilde{V}^{*}\sim 10^{−1}$ (with $\mu_{S}\approx 0.37$). Again, the separation between the different dynamic behaviors $\text{II}$/$\text{III}$ matches the experiment. The results are summarized schematically in Fig. 5(a) where $\widetilde{\dot{\gamma}}$ (~ $0.3$) is obtained from the intersection $\mu_{1}$ with the curve $\mu(\dot{\gamma})$ in the unstable region.
我们还可以在图 3(d) 中对具有较大颗粒的系统估算特征速度,此时 $\mu/\mu_{S} = 0.73$(区域 $\text{II}$),$\widetilde{V}^{*}$ 约为 $10^{−1}$(其中 $\mu_{S}\approx 0.37$)。同样,不同动态行为 $\text{II}$/$\text{III}$ 之间的分离与实验相吻合。结果在图 5(a) 中以示意图形式总结,其中 $\widetilde{\dot{\gamma}}$(~ $0.3$)是通过在不稳定区域与曲线 $\mu(\dot{\gamma})$ 相交处得到的 $\mu_{1}$ 来获得的。
Rearrangement of grains unjammed by ultrasound
As mentioned above, in a confined granular material, ultrasound can weaken the shear contact stiffness via microslip at grain contacts, inducing the frictional dissipation and reducing the material rigidity.
For a single grain under gravity, such shear ultrasound-induced decrease of the stuck area of a (hertzian) contact results in sliding below the static threshold. We surmise that a similar mechanism is at work here for the granular layer on the macroscopic scale.
如上所述,在束缚的颗粒材料中,超声波可通过颗粒间接触处的微滑动减弱剪切接触刚度,诱发摩擦耗散并降低材料刚度。
对于重力作用下的单个颗粒,这种由超声波引起的剪切接触(Hertz)粘滞面积的减小会导致低于静态阈值的滑动。我们推测,在宏观尺度上的某一颗粒层也有类似的机制在起作用。
As indicated above in Eq. $\eqref{eq1}$, the static friction coefficient $\mu_{S} = \mu_{p} + \mu_{g}( = \tan{\theta_{m}})$ includes both the interparticle friction $\mu_{p}$ and the geometric trapping $\mu_{g}$ (dilatancy effect).
Because of the small amplitude of ultrasound, the sound- matter interaction only modifies $\mu_{p}$ but not $\mu_{g}$, hence $\mu_{S}^{*} = \mu_{p}^{*} + \mu_{g}$.
From the Mindlin friction model, we have shown that decreases of both the shear contact stiffness $\Delta k_{t} /k_{t}$ and the interparticle friction coefficient $\Delta\mu_{p}/\mu_{p}$ are approximately proportional to ~ $− f_{t} /(\mu_{p}f_{n})$, where $f_{t}$ is the oscillating tangential force and $f_{n}$ the static normal force at a single contact.
如 $\eqref{eq1}$ 中所示,静摩擦系数 $\mu_{S} = \mu_{p} + \mu_{g}( = \tan{\theta_{m}})$ 包括颗粒间摩擦 $\mu_{p}$ 和几何阻挫 $\mu_{g}$(膨胀效应)两部分。
由于超声波振幅较小,声-物质相互作用仅改变 $\mu_{p}$ 而不影响 $\mu_{g}$,因此 $\mu_{S}^{*} = \mu_{p}^{*} + \mu_{g}$。
根据 Mindlin 摩擦模型,我们已经表明剪切接触刚度 $\Delta k_{t} /k_{t}$ 和颗粒间摩擦系数 $\Delta\mu_{p}/\mu_{p}$ 的减小大致与 $− f_{t} /(\mu_{p}f_{n})$ 成比例,其中 $f_{t}$ 是振荡切向力,$f_{n}$ 是单个接触处的静态法向力。
Such a scaling of vibration-induced softening ~ $−F_{ac}/(\mu_{p}W)$ can also be generalized to the effective shear contact stiffness at a multicontact interface between solids and to the shear modulus and the yield stress in a vibrated granular medium where polydisperse contact asperities are replaced by grain contacts and inertial effects are negligible.
振动诱导软化 ~ $-F_{ac}/(\mu_{p}W)$ 的这种比例关系也可以推广到固体间多接触界面的等效剪切接触刚度,以及振动颗粒介质中的剪切模量和屈服应力,在这种介质中,多分散接触表面被颗粒接触取代,惯性效应可以忽略不计。
Here $F_{ac}$ is the imposed macroscopic oscillating shear force, $W$ the normal load, and $\mu$ the (averaged) effective interparticle friction coefficient. Accordingly, we adopt here this scaling formula for the granular layer to describe the reduction of $\Delta\mu_{p}/\mu_{p}\sim −F_{ac}/(\mu_{p}W)$, which implies that $\mu_{S}^{*}/\mu_{S}$ ~ 1 − $F_{ac}/(\mu_{S}W)$.
这里的 $F_{ac}$ 是施加的宏观振荡剪切力,$W$ 是法向载荷,$\mu$ 是(平均的)等效颗粒间摩擦系数。因此,我们在此采用颗粒层的缩放公式来描述 $\Delta\mu_{p}/\mu_{p}\sim -F_{ac}/(\mu_{p}W)$,这意味着 $\mu_{S}^{*}/\mu_{S}$ ~ 1 - $F_{ac}/(\mu_{S}W)$。
For the granular layer considered here [Fig. 1(b)], we may write the above shear oscillating force by $F_{ac} = \hat{k}\hat{U}$ with $\hat{k}$ the effective stiffness of the granular layer and $\hat{U}$ the averaged displacement amplitude of shear vibration over the thickness $h(\approx 1.5\text{ mm})$.
对于这里所考虑的颗粒层[图 1(b)],我们可以用 $F_{ac} = \hat{k}\hat{U}$ 来表达上述剪切振动力,其中 $\hat{k}$ 是颗粒层的等效刚度,$\hat{U}$ 是厚度 $h(\approx 1.5\text{ mm})$ 上剪切振动的平均位移振幅。
To evaluate $\hat{U}$ , we assume the ultrasound amplitude at a distance $z$ from the transducer to be given by $U(z)\sim U_{0}\text{exp}(−z/\delta)$ with $U_{0}$ the source amplitude and $δ$(~ $\lambda = c/f$) the attenuation length dominated by wave scattering.
为了评估 $\hat{U}$ ,我们假设距离换能器 $z$ 处的超声波振幅由 $U(z)\sim U_{0}\text{exp}(-z/\delta)$ 给出,其中 $U_{0}$ 为声源振幅,$δ$(~ $\lambda = c/f$) 为由波散射主导的衰减长度。
Thus we have $\hat{U} = (1/h)\int_{0}^{h}U_{0}\text{exp}(-z/\delta)\mathrm{d}z = (\delta/h)U_{0}[1 - \text{exp}(-h/\delta)]$. With a wave speed $c\sim 10\text{ m/s}$ and ultrasound frequency $f = 70\text{ kHz}$, the wavelength is $\lambda\sim 0.15\text{ mm}$, leading to $\delta$ much less than $h$ and consequently $\hat{U}\sim (\delta/h)U_{0}\sim (c/ fh)U_{0}$.
因此,我们得到 $\hat{U} = (1/h)\int_{0}^{h}U_{0}\text{exp}(-z/\delta)\mathrm{d}z = (\delta/h)U_{0}[1 - \text{exp}(-h/\delta)]$ 。在波速为 $c\sim 10\text{ m/s}$ 和超声波频率为 $f = 70\text{ kHz}$ 时,波长为 $\lambda\sim 0.15\text{ mm}$,导致 $\delta$ 远远小于 $h$,因此 $\hat{U}\sim (\delta/h)U_{0}\sim (c/fh)U_{0}$。
Using an estimate for $W\sim (\rho gh)L^{2}$ with $L$ the width of the ultrasonic transducer [Fig. 1(b)] and $\rho$ the density of medium, and the relation between the effective stiffness and shear modulus of the layer $\hat{k}\sim G(L^{2}/h)$ as well as the sound speed $c = (G/\rho)^{1/2}$, we obtain the following expression:
$$ \mu_{S}^{*}/\mu_{S} \approx 1 - \frac{c^{3}}{g}\frac{U_{0}}{\mu_{S}fh^{3}}\tag{3}\label{eq3} $$
利用估计值 $W\sim (\rho gh)L^{2}$ (其中 $L$ 是超声波换能器的宽度[图 1(b)],$\rho$ 是介质的密度),以及层的等效刚度和剪切模量 $\hat{k}\sim G(L^{2}/h)$ 和声速 $c = (G/\rho)^{1/2}$ 之间的关系,我们可以得到以下表达式:
$$ \mu_{S}^{*}/\mu_{S} \approx 1 - \frac{c^{3}}{g}\frac{U_{0}}{\mu_{S}fh^{3}} $$
Equation $\eqref{eq3}$ contains the sufficient dependencies for rescaling the experimental data for various layer thicknesses and ultrasound amplitudes and frequencies [Fig. 4(c)].
The roughness of the transducer surface shall pin a small fraction of the grains in the vicinity of the solid surface and increase the effect of local dilatancy by the parameter $\mu_{g}$, therefore decreasing the slope in Eq. $\eqref{eq3}$, provided that $\mu_{p}$ is similar for all the systems studied.
方程 $\eqref{eq3}$ 包含了对不同层厚、超声振幅和频率的实验数据进行重新标定的充分依赖关系[图 4(c)]。
换能器表面的粗糙度会将固体表面附近的一小部分颗粒夹住,并通过参数 $\mu_{g}$ 增加局部扩张的效果,从而减小公式 $\eqref{eq3}$ 中的斜率,前提是 $\mu_{p}$ 对所有研究的系统都是相似的。
This predicted scaling agrees with the observation in Fig. 4(c) in which rougher surface (higher $\mu_{S}$) requires larger vibration amplitude ($U_{0}$) to provoke the grain motion from jammed to unjammed states. Moreover, by fitting the mean slope of the rescaled plot in Fig. 4(d) (black dashed line), we may estimate from Eq. $\eqref{eq3}$ the wave speed $c = 20 \pm 5 (\text{m/s})$, which agrees well with those found in the previous works.
这种预测的比例与图 4(c) 中的观察结果一致,即粗糙的表面(更高的 $\mu_{S}$)需要更大的振动振幅($U_{0}$)才能引起颗粒从堵塞态运动到非堵塞态。此外,通过拟合图 4(d) 中重标定曲线的平均斜率(黑色虚线),我们可以从公式 $\eqref{eq3}$ 中估算出波速 $c = 20 \pm 5 (\text{m/s})$,这与之前的研究结果非常吻合。
Nevertheless, the points remain scattered after rescaling in Fig. 4(d) ($\Delta c/c\sim 25\%$). More comprehensive studies are required in future investigation to quantify the effects of the layer thickness and ultrasound frequency for a better understanding of the unjamming transition between region $\text{I}$ and region $\text{II}$/$\text{III}$ [Fig. 1(c)].
尽管如此,图 4(d) 中的点在重新缩放后仍然是分散的($\Delta c/c\sim 25%$)。为了更好地理解 $\text{I}$ 区域和 $\text{II}$/$\text{III}$ 区域[图 1(c)]之间的解堵塞过渡,需要在未来的研究中进行更全面的研究,量化 层厚度 和 超声频率 的影响。
Since we did not detect any effect of the polarization of the ultrasounds, the phenomenology observed here is similar to Ref. [42], where ultrasound was shown to play the role of an effective temperature in the unjamming diagram. The analysis shows that the static threshold of granular layers is lowered by ultrasound via the decrease of the interparticle friction coefficient, resulting in the remarkable alteration of the dynamics at the macroscale with the triggering of granular avalanches.
由于我们没有检测到超声波极化的任何影响,因此这里观察到的现象与参考文献 [42] 相似。文献 [42] 显示,超声波在解堵塞图中起到了有效温度的作用。分析表明,超声波通过减小颗粒间的摩擦系数降低了颗粒层的静态阈值,从而显著改变了宏观尺度上的动力学,引发了颗粒雪崩。
CONCLUSION
In summary, we have investigated the flow of granular layers triggered by nanometer-amplitude ultrasound below the threshold. When the angle of inclination is far below the angle of repose $\theta_{r}$, the ultrasound induces highly fluctuating grain motions with a small average flow velocity.
As opposed to shaking experiments, grain motions do not correspond to geometrical rearrangements such as jumps forced by the oscillations, but rather to jigglings or agitations in traps formed by neighbors thanks to the small potential energy released from the decrease of interparticle friction $\mu_{p}$ by the shear acoustic lubrication at grain contacts.
This sound-matter interaction depends on ultrasound frequency and layer thickness due to wave attenuation, as well as on the transducer surface roughness which pins the grains by the dilatancy effect.
总结一下,我们研究了在纳米振幅超声作用下触发的颗粒层的流动,位于阈值以下。当倾斜角远低于休止角 $\theta_{r}$ 时,超声引发颗粒小的平均流动速度, 高标准差的运动。
与振动实验不同,颗粒运动不对应于由振动强制引起的几何重排,而更类似于由于颗粒间摩擦 $\mu_{p}$ 由颗粒接触处的剪切声润滑导致的小势能释放而形成的陷阱中的摇晃或搅动。
这种声-物质相互作用取决于超声频率和层厚度,因为存在波衰减,以及换能器表面粗糙度通过膨胀效应将颗粒固定在位。
Close below the angle of repose, we observe the triggered flow with a larger averaged velocity increasing with the ultrasound amplitude, owing to the reduction of the granular threshold $\mu_{S}$ via the decrease of interparticle friction $\mu_{p}$. This creeplike flow can be sustained only by a prolonged excitation and arrests when ultrasound is turned off. At higher inclination, close to $\theta_{m}$, triggered avalanches are fast and continuous with a flow velocity independent of the applied ultrasound; it is dominated by the inertial self-generated dynamics of the granular system. These experimental observations agree with the predictions of any velocity-weakening friction model, consistent with the picture of the unjamming transition.
在低于且接近休止角时,我们观察到被诱发(的颗粒)流动,其平均速度随超声振幅的增加而增大,这是由于颗粒阈值 $\mu_{S}$ 通过颗粒间摩擦力 $\mu_{p}$ 的减小而降低。这种蠕变流动只能通过长时间的激励来维持,并在超声关闭时停止。在更高的倾角,接近 $\theta_{m}$ 时,触发的雪崩是快速和连续的,其流速与施加的超声波无关;它由颗粒系统的惯性自发动力学主导。这些实验观察结果与任何速度减弱摩擦模型的预测结果一致,符合解堵塞转变的描述。
We believe that this work provides a unified picture of the behavior of vibrated granular matter. The multiscale analysis will be useful to better understand the local and remote dynamic triggering of landslides and earthquakes by seismic waves, including aftershocks.
我们相信,这项工作为受振颗粒物质的行为提供了一个统一的绘景。多尺度分析将有助于更好地理解地震波(包括余震)对滑坡和地震的局域和远程动态触发。

