DOI: 10.1038/ncomms15991
Abstract
Friction plays a key role in how ruptures unzip faults in the Earth’s crust and release waves that cause destructive shaking. Yet dynamic friction evolution is one of the biggest uncertainties in earthquake science. Here we report on novel measurements of evolving local friction during spontaneously developing mini-earthquakes in the laboratory, enabled by our ultrahigh speed full-field imaging technique. The technique captures the evolution of displacements, velocities and stresses of dynamic ruptures, whose rupture speed range from sub-Rayleigh to supershear.
The observed friction has complex evolution, featuring initial velocity strengthening followed by substantial velocity weakening. Our measurements are consistent with rate-and-state friction formulations supplemented with flash heating but not with widely used slip-weakening friction laws. This study develops a new approach for measuring local evolution of dynamic friction and has important implications for understanding earthquake hazard since laws governing frictional resistance of faults are vital ingredients in physically-based predictive models of the earthquake source.
摩擦力在地壳断裂如何拉开断层并释放导致破坏性震动的波动中起着关键作用。然而,动态摩擦演化是地震科学中最大的不确定性之一。在此,我们报告了在实验室自发发展的小型地震中,利用超高速全场成像技术对不断演变的局部摩擦力进行的新测量。该技术可捕捉动态断裂的位移、速度和应力的演变,其断裂速度范围从亚 Rayleigh 到超剪切。
观测到的摩擦具有复杂的演变过程,最初速度增强,随后速度大幅减弱。我们的测量结果符合辅以闪加热的速率-状态摩擦公式,但不符合广泛使用的滑动减弱摩擦定律。这项研究开发了一种测量局部动态摩擦演变的新方法,对了解地震灾害具有重要意义,因为断层摩擦阻力定律是基于物理的震源预测模型的重要组成部分。
Introduction
Large destructive earthquakes are typically caused by dynamic rupture propagating along pre-existing faults in the Earth’s crust, such as the San Andreas Fault in California that appears to be ready for the next big earthquake. During such rupture, the two sides of the fault slide past each other, accumulating relative displacement—or slip—with average slip velocities of the order of $1 \text{ m s}^{-1}$.
This marked process is heavily affected by dynamic friction and its dependence on rapidly evolving rupture parameters such as slip and slip rate. That is why dynamic friction is a key aspect of earthquake physics and a crucial input to models of both single dynamic ruptures and long-term earthquake behaviour. Assumptions about dynamic friction can markedly change the interpretation of earthquake observations, leading to different conclusions about the physical mechanisms controlling rupture speeds, rupture modes, stress levels on faults, and patterns of seismic/aseismic slip.
大型破坏性地震通常是由沿地壳中原已存在的断层传播的动态断裂引起的,例如 California 州的 San Andreas 断层似乎已经为下一次大地震做好了准备。在这种断裂过程中,断层两侧相互滑动,累积相对位移或滑移,平均滑移速度约为 $1 \text{ m s}^{-1}$。
这一明显的过程受到动摩擦力及其对快速变化的断裂参数(如滑移和滑移率)的严重影响。这就是为什么动摩擦是地震物理学的一个关键方面,也是单次动态破裂和长期地震行为模型的一个重要输入。关于动态摩擦的假设可能会明显改变对地震观测结果的解释,导致对控制破裂速度、破裂模式、断层应力水平以及地震/抗震滑移模式的物理机制得出不同的结论。
From theoretical and numerical studies, it is clear that friction needs to weaken for earthquake rupture to nucleate and proceed, but the detailed nature of appropriate friction laws are an active area of current study. One of the commonly used friction formulations is slip weakening, in which friction decreases from a peak value to a residual value with increasing slip across the frictional interface. The formulation is a convenient and intuitive extension of the basic notions of static/kinetic friction and it is still actively used for numerical simulations, theoretical considerations and interpreting observations.
Higher-resolution experiments on propagating shear rupture show a more complex friction evolution with slip, with initial slip strengthening, followed by slip weakening. More elaborate slip-dependent friction models have been proposed to fit these details. At the same time, a number of lab experiments have demonstrated significant dependence of friction on slip velocity, often mixed in with other effects.
Such friction experiments typically impose slip-velocity histories to the sample, assume uniform sliding along the interface, and measure the resulting averaged friction resistance. The expected friction evolution during earthquakes is determined from such measurements through formulations of empirical friction laws and subsequent dynamic rupture modeling.
从理论和数值研究来看,摩擦力显然需要减弱才能使地震破裂成核并继续进行,但适当摩擦力定律的详细性质是当前研究的一个活跃领域。常用的摩擦公式之一是滑动减弱法,即随着摩擦界面滑动的增加,摩擦力从峰值下降到残值。该公式是对静摩擦/动摩擦基本概念的方便直观的扩展,目前仍被积极用于数值模拟、理论考虑和解释观测结果。
更高分辨率的剪切破裂传播实验表明,摩擦力随滑移的演变更为复杂,最初滑移加强,随后滑移减弱。为了适应这些细节,人们提出了更复杂的随滑移变化的摩擦模型。与此同时,一些实验室实验也证明了摩擦力与滑移速度的显著相关性,而且往往与其他效应混合在一起。
此类摩擦实验通常对样本施加滑动速度历史,假设沿界面均匀滑动,并测量由此产生的平均摩擦阻力。通过制定经验摩擦定律和随后的动态断裂建模,可根据此类测量结果确定地震期间的预期摩擦演化。
Here we present and analyse our experimental measurements of local friction during spontaneously evolving dynamic rupture in a laboratory earthquake set-up. Although not spontaneously generated, our ruptures are spontaneously evolving, in the sense that their slip, slip rate, and shear stress evolution are not imposed but rather determined by the fault prestress, fault friction, and dynamic stress transfer during rupture. This is an important property of our experiments, since, typically, frictional studies are conducted by imposing the slip rate, slip, or stress histories.
在此,我们介绍并分析了在实验室地震装置中对自发演化的动态断裂过程中局部摩擦力的实验测量结果。虽然不是自发产生的,但我们的破裂是自发演化的,即其滑移、滑移率和剪应力演化不是强加的,而是由破裂过程中的断层预应力、断层摩擦力和动态应力传递决定的。这是我们实验的一个重要特性,因为摩擦研究通常是通过施加滑移率、滑移或应力历史来进行的。
By capturing evolving friction as well as slip and slip rate during dynamic rupture of the laboratory fault, we can directly study the dependence of dynamic friction on slip and/or slip rate evolution characteristic of spontaneously evolving rupture. These measurements are enabled by our ultrahigh speed technique for imaging full-field spatial and temporal variations in displacements of the laboratory sample, from which we can infer full-field maps of stresses and particle velocities.
通过捕捉实验室断层动态破裂过程中摩擦力以及滑移和滑移率的演变,我们可以直接研究动态摩擦力对滑移的依赖性和/或自发演变破裂的滑移率演变特征。我们的超高速技术可对实验室样本位移的全场空间和时间变化进行成像,并从中推断出应力和颗粒速度的全场图,从而实现这些测量。
Results
Dynamic imaging of earthquakes in the laboratory
The spontaneously evolving dynamic ruptures are produced in the laboratory earthquake set-up that mimics the main features of a fault in the Earth’s crust (Fig. 1). The fault is simulated by an interface inclined at an angle $\alpha$ and prestressed both in shear and compression due to far-field load $P$, simulating tectonic stresses (as discussed further in the ‘Laboratory earthquake set-up’ section in Methods).
自发演化的动态断裂是在模拟地壳断层主要特征的实验室地震装置中产生的(图 1)。断层是由一个倾斜角度为 $\alpha$ 的界面模拟的,由于远场荷载 $P$,该界面受到剪切和压缩预应力,模拟构造应力(在方法中的 “实验室地震装置 “部分有进一步讨论)。
Dynamic ruptures are nucleated due to the local pressure release provided by a rapid expansion of a NiCr wire filament due to an electrical discharge. To enable dynamic rupture initiation within a smaller, laboratory-scale sample, we use an analogue material, Homalite, which has a significantly ($\sim 20$ times) lower shear modulus compared to rocks. This is an important experimental advantage, since it significantly decreases all relevant critical length scales, such as the critical crack size and rupture nucleation size, allowing us to study well-developed shear ruptures in samples of tens of centimeters, instead of several meters as would be required for rocks.
动态断裂是由于 NiCr 丝在放电过程中快速膨胀所产生的局部压力释放而形成的。为了能够在实验室规模较小的样品中引发动态断裂,我们使用了一种类似材料–高铝酸盐,它的剪切模量比岩石低很多($\sim 20$ 倍)。这是一个重要的实验优势,因为它大大降低了所有相关的临界长度尺度,如 临界裂缝尺寸 和 破裂成核尺寸,使我们能够在几十厘米的样本中研究良好发展的剪切破裂,而不是像岩石那样需要几米的样本。
Previous versions of this laboratory earthquake set-up have been successfully employed to study a number of key dynamic rupture phenomena, including supershear transition, rupture directionality and limiting speeds due to bimaterial effect, off-fault attenuation and damage creation, and pulse-like to crack-like transition.
该实验室地震装置的前几版已成功用于研究一系列关键的动态破裂现象,包括超剪切过渡、双材料效应导致的破裂方向性和极限速度、断层外衰减和损伤产生,以及脉冲样向裂缝样过渡。
The measurements presented here are enabled by our newlydeveloped technique for full-field imaging of dynamic ruptures (Figs 1 and 2). The specimen surface is coated by a carefully selected speckle pattern to produce a characteristic texture in the digital images. Digital images of the patterns distorted by the propagating rupture are acquired by a high-speed camera chosen for its lowest noise after an extensive comparison; 128 images are obtained with temporal sampling of 2 million frames per s. The sequence of images is turned into evolving displacement maps using the digital image correlation (DIC) method further developed for our experiments (see ‘Full-field imaging of dynamic ruptures’ section in Methods).
我们新开发的动态破裂全场成像技术(图 1 和图 2)使本文介绍的测量成为可能。试样表面涂有精心挑选的斑点图案,以便在数字图像中产生特征纹理。经过广泛比较后,我们选择了噪音最低的高速相机来获取被破裂传播扭曲的图案的数字图像;我们以每秒 200 万帧的时间采样率获取了 128 幅图像,并使用为我们的实验进一步开发的 数字图像相关(DIC)方法将图像序列转化为不断变化的位移图(见 “方法 “中的 “动态破裂的全场成像 “部分)。
The particle velocity and strain change maps are obtained through time and space differentiation of the displacement fields, respectively; the stress change maps are computed from the strain maps using known linear-elastic and high-strain-rate properties of the material tested (Fig. 1). To study friction evolution, we track the time history of the ratio of shear to normal stress along the fault (which gives the friction coefficient) together with those of slip and slip rate across the interface. The total stresses are computed by adding the (non-uniform) stress changes inferred from the imaging and (uniform) prestress values computed from the imposed far-field load $P$ and inclination angle a (see section ‘Post-processing of the displacement fields’ in Methods).
质点速度和应变变化图分别通过位移场的时间和空间微分获得;应力变化图是根据应变图,利用测试材料的已知线弹性和高应变率特性计算得出的(图 1)。为了研究摩擦力的演变,我们跟踪了断层沿线剪应力与法向应力之比(即摩擦系数)的时间历史,以及界面上的滑移和滑移率。总应力的计算方法是:将成像推断出的(非均匀)应力变化与根据外加远场荷载 $P$ 和倾角 a 计算出的(均匀)预应力值相加(见 “方法 “中 “位移场的后处理” 一节)。
The uniform distribution of prestresses in our experiments has been verified in earlier studies directly using photoelasticity and indirectly through repeatability of ruptures in different experiments performed under the same far-field experimental loading. The uniformity of prestress is further supported by the near-steady rupture propagation through our observation window as discussed in the following.
我们实验中预应力的均匀分布已在先前的研究中通过光弹性直接得到验证,并通过在相同远场实验荷载下进行的不同实验中断裂的可重复性间接得到验证。预应力的均匀性还得到了通过我们的观测窗口进行的近乎稳定的断裂传播的进一步支持,这将在下文中讨论。
The full-field images reveal the details of rupture propagation within the entire deformation window with a spatial and temporal resolution that was previously obtainable only in numerical simulations (Fig. 1; Supplementary Movie 1). By following the rupture tip travelling along the interface, we can determine the rupture speed. For example, in the experiment presented in Fig. 1, we find that the rupture is supershear, as evident by the Mach cone features observed in the shear stress maps. We have verified the accuracy of the full-field DIC measurements by comparing the velocity time-histories at selected locations (Fig. 3) with simultaneous, independent point-wise measurements using the well-developed technique of laser velocimetry.
全场图像揭示了破裂在整个变形窗口内传播的细节,其空间和时间分辨率以前只能在数值模拟中获得(图 1;补充影片 1)。通过跟踪沿界面移动的断裂尖端,我们可以确定断裂速度。例如,在图 1 所示的实验中,我们发现破裂是超剪切的,这从剪应力图中观察到的 Mach 锥特征可以看出。我们通过比较选定位置的速度时间历程(图 3)和使用成熟的激光测速技术进行的同步独立点测量,验证了全场 DIC 测量的准确性。
The DIC and laser-velocimeter measurements are in excellent agreement (Fig. 3b), a remarkable development since the laser velocimeters are specifically designed to accurately resolve the rapid variations in particle velocities. However, because of the cost and laser arrangements involved, it is only feasible to employ 2–3 velocimeters in each experiment. Now, the validated DIC technique provides us with tens of thousands of time-history measurements arranged into a two-dimensional spatial picture of particle velocities, deformations, and stresses, enabling further insight into a range of dynamic earthquake phenomena that can be studied with this experimental set-up. For example, the full-field data can be used to study how rapidly the motion attenuates away from the fault for different rupture scenarios, an important aspect of seismic hazard assessment.
DIC 和激光测速仪的测量结果非常吻合(图 3b),这是一个显著的进步,因为激光测速仪是专门为精确分辨粒子速度的快速变化而设计的。然而,由于涉及到成本和激光排列,每次实验只能使用 2-3 个测速仪。现在,经过验证的 DIC 技术为我们提供了数以万计的时间历史测量数据,这些数据被排列成颗粒速度、变形和应力的二维空间图像,使我们能够进一步深入了解通过这种实验装置可以研究的一系列动态地震现象。例如,全场数据可用于研究不同断裂情况下运动远离断层的衰减速度,这是地震灾害评估的一个重要方面。
Evolution of dynamic friction with slip
Here we focus on the evolution of dynamic friction, and specifically whether it is controlled by slip or slip rate. Our experimental set-up enables us to produce spontaneously evolving dynamic ruptures with significantly different slip-rate histories, which result in remarkably different friction behaviour (Figs 4 and 5). We start by analysing two tests conducted under two different far-field loading conditions ($P = 7.4$ and $23\text{ MPa}$) but the same inclination angle $\alpha = 29°$; both cases result in supershear ruptures.
在这里,我们重点研究动态摩擦力的演变,特别是它是由滑移还是滑移率控制的。我们的实验装置使我们能够产生具有明显不同滑移率历史的自发演化动态断裂,从而产生明显不同的摩擦行为(图 4 和图 5)。我们首先分析了在两种不同的远场加载条件($P = 7.4$ 和 $23\text{MPa}$)下进行的两次试验,但倾角相同,均为 $\alpha = 29°$;两种情况都导致了超剪切破裂。
For the two loads, rupture exhibits a rapid increase of slip rates towards a peak value and subsequent decay to near-constant values (Figs 4a and 5c), although the level of slip rates is quite different between these two cases: the peak slip rate is $\sim 2$ and $\sim 20{ m s}^{-1}$ for the lower and higher load case, respectively. The rupture produced by the higher far-field load also has a higher overall level of shear stress and a more pronounced reduction in shear stress compared to the lower load case (Fig. 4b). Note that in both cases, as the rupture front approaches, the shear stress initially increases with slip rate, from its static pre-stress level, and subsequently drops to a lower dynamic level.
对于这两种载荷,破裂表现出滑移率的快速增长,达到一个峰值,随后衰减到接近恒定值(图 4a 和 5c),尽管这两种情况下的滑移率水平有很大不同:较低和较高载荷情况下的峰值滑移率分别为 $\sim 2$ 和 $\sim 20{ m s}^{-1}$。与较低载荷情况相比,较高远场载荷产生的断裂也具有更高的整体剪应力水平和更明显的剪应力减小(图 4b)。需要注意的是,在这两种情况下,当破裂前沿接近时,剪应力从静态的预应力水平开始随滑移速率增加,随后下降到较低的动态水平。
The dependence of friction on slip in the two experiments described above is displayed in (Fig. 5a). For each of these experiments, this dependence qualitatively resembles that described by a linear slip-weakening friction law. However, the variation of friction with slip is drastically different in the two cases, demonstrating that a unique, purely slip-dependent law cannot describe the frictional characteristics of the interface. Indeed, all of our experiments, when reviewed collectively, do not support slip weakening as the operant law in friction.
图 5a 显示了上述两个实验中摩擦力与滑移的关系。在每个实验中,这种依赖关系都与线性滑移减弱摩擦定律所描述的情况非常相似。然而,在这两种情况下,摩擦力随滑移的变化却大相径庭,这表明一个独特的、纯粹依赖滑移的定律无法描述界面的摩擦特性。事实上,我们的所有实验综合起来看,都不支持将滑动减弱作为摩擦的主要规律。
To illustrate this further, let us consider another experiment, with the far-field loading $P = 12\text{ MPa}$ and inclination angle $\alpha =24°$, which features a sub-Rayleigh pulse-like rupture followed by a supershear crack-like rupture, as evidenced by the slip-rate history (Fig. 4c). In this experiment, once nucleated, the rupture propagates bilaterally along the interface, with two rupture tips traveling in opposite directions. The rupture traveling towards the higher edge of the specimen, and through our imaging region, propagates as a pulse at sub-Rayleigh speeds. The timing analysis shows that the following supershear crack-like rupture is the result of the other rupture tip reflecting from the specimen lateral surface and transitioning to supershear speeds; it then enters our imaging region.
为了进一步说明这一点,让我们考虑另一个实验,远场载荷为 $P = 12text{ MPa}$,倾角为 $\alpha=24°$,从滑移率历史(图 4c)可以看出,该实验的特点是在亚 Rayleigh 脉冲样断裂之后出现超剪切裂纹样断裂。在该实验中,破裂一旦成核,就会沿界面向两侧传播,两个破裂尖端的传播方向相反。断裂向试样的较高边缘移动,并穿过我们的成像区域,以亚 Rayleigh 率速度作为脉冲传播。时序分析表明,接下来的超剪切裂纹状破裂是另一个破裂尖端从试样侧表面重新反射并过渡到超剪切速度的结果;然后它进入我们的成像区域。
As in the previous examples, the shear stress initially increases from its static prestress level, as the rupture front approaches, and then drops and eventually settles to a lower dynamic value (Fig. 4d). When the supershear crack-like rupture arrives, the interface slips at a higher rate and the shear stress evolves again in a similar pattern: it first increases and then drops. Hence, in this experiment, the friction evolution with slip exhibits two weakening episodes, associated with the passing of the two ruptures—the sub-Rayleigh pulse and the supershear crack (Fig. 5b,d). Again, a purely slip-weakening law is not capable of reproducing such complex friction behaviour.
与前面的例子一样,随着破裂前沿的接近,剪应力从静态预应力水平开始上升,然后下降,最终稳定在较低的动态值上(图 4d)。当超剪切裂纹状断裂到来时,界面以更高的速度滑动,剪应力再次以类似的模式演变:先增加后下降。因此,在本实验中,摩擦力随滑移的演变表现出两个减弱事件,与两个断裂–亚 Rayleigh 脉冲和超剪切裂纹–的通过有关(图 5b、d)。同样,纯粹的滑移减弱定律也无法解释如此复杂的摩擦行为。
Evolution of dynamic friction with slip rate
To further understand the features of observed friction, let us consider its variation with slip velocity (Fig. 6). Clearly, the friction evolution cannot be described by a purely rate-dependent law either; in fact, each case displays its own distinct hysteretic behaviour indicating strong sliding history dependence. Despite their differences, the two cases display qualitatively similar behaviour characterized by: (i) initial strengthening with the slip velocity, consistent with the direct effect of the rate-and-state friction formulations, (ii) subsequent strong weakening with slip velocity, and (iii) near constant level of dynamic friction that depends on the sustained value of the slip rates ( $f_{d}\sim 0.39$ for $V\sim 0.87\text{ m s}^1$ and $f_{d}\sim 26$ for $V\sim6.5\text{ m s}^1$). The second peak in the slip-rate function (Fig. 4a), which is likely due to the finite thickness of the specimen30, results in a secondary ’loop’ in the friction versus slip rate curves, with some strengthening (consistent with the direct effect of rate-and-state friction) followed by weakening. Note that the peak friction coefficient is not reached at incipient slip, as assumed in many slip-dependent friction formulations, but rather after slip has initiated on the interface.
为了进一步了解观察到的摩擦力特征,让我们考虑一下摩擦力随滑动速度的变化(图 6)。很明显,摩擦力的演变也不能用纯粹的速度相关定律来描述;事实上,每种情况都显示出其独特的滞后行为,表明了强烈的滑动历史依赖性。尽管存在差异,但这两种情况在性质上表现出相似的行为,其特征如下:
(i) 随着滑动速度的增加,摩擦力最初增强,这与速率-状态摩擦公式的直接效应一致, (ii) 随后随着滑动速度的增加,摩擦力大幅减弱, (iii) 动态摩擦力的近似恒定水平取决于滑移速率的持续值($f_{d}\sim 0.39$ 对应 $V\sim 0.87\text{ m s}^1$ 和 $f_{d}\sim 26$ 对应 $V\sim6.5\text{ m s}^1$)。滑移率函数中的第二个峰值(图 4a)可能是由于试样的有限厚度而导致的,这导致摩擦力与滑移速率曲线中出现了次级的 “回路”,其中一些增强(与速率-状态摩擦的直接效应一致)随后减弱。需要注意的是,许多依赖滑移的摩擦定律假设在初次滑移时达到峰值摩擦系数,而实际上是在界面上的滑移开始后才达到的。
Overall, this behaviour is qualitatively consistent with the rate-and-state friction laws, in which friction is the function of the slip rate and a state variable that describes the evolution of contact population (see section ‘On friction laws’ in Methods). In these laws, friction is rate-dependent after sufficient slip at a constant slip rate, but exhibits history-dependent transient effects during changes of velocity that are mathematically represented by the evolving state variable. During dynamic rupture, interfaces governed by the rate-and-state friction laws exhibit friction evolution similar to what occurs in our experiments, with the friction first increasing due to the direct effect, then decreasing due to evolution of the state variable, and then remaining constant for constant dynamic slip velocities due to friction being velocity-dependent in steady state.
总体而言,这种行为与速率-状态摩擦定律在性质上是一致的,其中摩擦力是滑移速率和描述接触群体演变的状态变量的函数(见 “方法” 中 “关于摩擦定律” 一节)。在这些定律中,摩擦力在以恒定的滑动速率充分滑动后与速率相关,但在速度变化期间则表现出与历史相关的瞬态效应,这些效应在数学上由不断变化的状态变量表示。在动态断裂过程中,受速率-状态摩擦定律支配的界面会表现出与我们的实验类似的摩擦演化,摩擦力首先因直接效应而增大,然后因状态变量的演化而减小,然后在恒定的动态滑移速度下保持不变,这是因为摩擦力在稳定状态下与速度有关。
Some slip-weakening formulations linked higher values of the effective weakening slip distance to higher values of normal stress. Our measurements indicate that the effective slip weakening depends on the slip-rate history rather than on the level of normal stress. In the experiment with a pulse-like rupture followed by a crack-like rupture, the two ruptures display a notably different effective weakening with slip (Fig. 5b), despite occurring at the same normal stress.
The same conclusion is reached by comparing two tests conducted under different levels of far-field loading $P$ and different inclination angle $\alpha$ but having the same level of resolved normal stress on the interface. The two tests are characterized by substantially different slip rate histories (Fig. 5d). The resulting friction versus slip evolution is substantially different, and the effective slip scale over which friction decreases is substantially different in the two experiments (Fig. 5b), despite the same normal stress, further substantiating the point that the slip-rate evolution is the dominating factor controlling the evolution of friction with slip.
一些滑移削弱公式将较高的有效削弱滑移距离值与较高的法向应力值联系起来。我们的测量结果表明,有效滑移削弱取决于滑移速率历史,而不是法向应力水平。在脉冲式破裂之后是裂缝式破裂的实验中,尽管发生在相同的法向应力下,两种破裂显示出明显不同的有效滑移削弱(图 5b)。
通过比较在不同的远场加载 $P$ 和不同的倾角 $\alpha$ 条件下进行的两次试验(但界面上的解析法向应力水平相同),可以得出相同的结论。这两次试验的滑移率历史记录大不相同(图 5d)。尽管法向应力相同,但摩擦力随滑移的变化却大相径庭,摩擦力减小的有效滑移尺度在两次试验中也完全不同(图 5b),这进一步证实了滑移率变化是控制摩擦力随滑移变化的主导因素这一点。
Near-steady rupture propagation through observation window
Our measurements show that the slip-rate and friction time histories considered are quite similar for different points along our observation window, indicating that the ruptures are steady and well-developed. To illustrate the similarity, we compare the time histories at the center of the field of view with two other locations along the interface, at a distance $d = 4.6\text{ mm}$ from the center of the imaged area (Fig. 7) and find that the time histories are nearly identical.
Hence the rupture is well-developed and steady when it enters our field of view, and our friction analysis does not depend on the location along the observation window. The fact that slip rate time histories at different locations along the interface are nearly identical supports a uniform distribution of normal and shear prestress along the interface, as a heterogeneous state of prestress would cause variations in the slip-rate time histories.
我们的测量结果表明,沿观测窗口的不同点的滑移率和摩擦力时间历程非常相似,这表明断裂是稳定且发展良好的。为了说明这种相似性,我们将视场中心的时间历程与沿界面的其他两个位置进行了比较,这两个位置距离成像区域中心的距离为 $d = 4.6\text{ mm}$(图 7),结果发现时间历程几乎相同。
因此,当断裂进入我们的视野时,断裂已经发展成熟并趋于稳定,而我们的摩擦分析并不依赖于沿观测窗口的位置。沿界面不同位置的滑移率时间历程几乎相同,这一事实证明法向和剪切预应力沿界面均匀分布,因为预应力的异构状态会导致滑移率时间历程的变化。
Enhanced dynamic weakening
Values of friction achieved in our experiments at different constant slip rates reveal pronounced weakening with slip rate (Fig. 8a) suggesting activation of enhanced dynamic weakening in our experiments. For example, at the higher sustained slip rate ($V\sim 6.5\text{ m s}^{-1}$), the friction coefficient decreases from a peak value of $\sim 0.63$ down to $\sim 0.26$, variation that cannot be explained with standard, logarithmic rate-and-state formulations that generally result in mild friction changes (see sections ‘Steady-state friction analysis’ and ‘On friction laws’ in Methods).
我们的实验在不同的恒定滑移率下获得的摩擦力值显示,随着滑移率的增加,摩擦力明显减弱(图 8a),这表明我们的实验激活了增强的动态减弱。例如,在较高的持续滑动速率下($V\sim 6.5\text{ m s}^{-1}$),摩擦系数从峰值 $\sim 0.63$ 下降到 $\sim 0.26$,这种变化无法用标准的对数速率-状态公式来解释,因为这种公式通常会导致轻微的摩擦变化(见方法中的 “稳态摩擦分析 “和 “摩擦定律 “部分)。
We find that our results are consistent with a combined formulation of rate-and-state friction enhanced with flash heating weakening (Fig. 8a). Flash heating is a dynamic mechanism in which tips of the contacting asperities heat up and dramatically weaken due to shear, resulting in a pronounced, $1/V$, dependence of friction in slip velocity $V$:
$$ \begin{equation} f = f_{w} + (f_{0} - f_{w}) V_{w} / V\tag{1} \end{equation} $$
where $V_{w}$ and $f_{w}$ are the weakening slip velocity and the residual friction coefficient, respectively, and $f_{0}$ is the friction coefficient for $V<V_{w}$. In the combined formulation of rate-and-state friction enhanced with flash heating weakening, the low-velocity friction coefficient $f_{0}$ of equation (1) is described by rate-and-state friction (see section ‘On friction laws’ in Methods). In fitting the experimental results with the rate-and-state and combined formulations, we use the rate-and-state properties constrained for Homalite interfaces by low-velocity friction experiments39 (Fig. 8a).
我们发现,我们的结果与速率-状态摩擦增强与闪热削弱的组合公式一致(图 8a)。闪蒸加热是一种动态机制,在这种机制下,接触表面的尖端会因剪切力而升温并急剧减弱,从而导致摩擦力与滑移速度 $V$ 的关系达到 $1/V$ 的明显程度:
$$ \begin{equation} f = f_{w} + (f_{0} - f_{w}) V_{w} / V\tag{1} \end{equation} $$
其中 $V_{w}$ 和 $f_{w}$ 分别是削弱滑移速度和残余摩擦系数,$f_{0}$ 是 $V<V_{w}$ 时的摩擦系数。在速率-状态摩擦增强与闪热减弱的组合公式中,方程(1)中的低速摩擦系数 $f_{0}$ 是由速率-状态摩擦来描述的(见 “方法” 中 “关于摩擦定律” 一节)。在将实验结果与速率-状态公式和组合公式进行拟合时,我们使用了低速摩擦实验39(图 8a)对霍马来石界面进行约束的速率-状态特性。
Hence our measurements clearly indicate that friction weakens with slip rate much more prominently than predicted by logarithmic rate-and-state friction laws. While our data are consistent with the combined formulation of rate-and-state friction enhanced by flash weakening, we are not able to determine whether the actual physical mechanism operating is indeed flash heating, and there may be other enhanced velocity-weakening mechanisms at play. Note that the systematic rate dependence shown in Fig. 8a contains points from both sub-Rayleigh and supershear ruptures, which have quite different elastodynamic stress fields, but propagate over the interface with the same preparation and hence the same friction properties.
因此,我们的测量结果清楚地表明,摩擦力随滑动速率的减弱比对数速率-状态摩擦定律所预测的要明显得多。虽然我们的数据与闪热减弱所增强的速率-状态摩擦的组合公式一致,但我们无法确定实际的物理机制是否真的是闪热,可能还有其他增强的速度减弱机制在起作用。请注意,图 8a 中显示的系统速率依赖性包含了来自亚雷利率和超剪切破裂的点,这两种破裂的弹性应力场截然不同,但在界面上传播时具有相同的制备,因此具有相同的摩擦特性。
It is remarkable that the inferred enhanced velocity-weakening parameters are consistent with the previous experimental study of Lu et al. that constrained the steady-state rate-weakening properties of our experimental interfaces based on how the rupture changes from crack-like to pulse-like as the nondimensional interface prestress, in terms of the ratio of the resolved normal to shear stress, is reduced.
The origin of the pulse-like mode of rupture propagation in natural earthquakes is a key issue in earthquake physics. Enhanced velocity weakening due to flash heating has been predicted to produce pulse-like ruptures on interfaces with low prestress, suggesting that such weakening can both explain the origin of slip pulses and resolve the heat paradox. Our direct measurements of the evolving friction confirm the conclusions of Lu et al. that the pulse-like ruptures observed in their experiments for lower nondimensional prestresses are due to substantial velocity weakening of friction. Indeed, our experiments feature a main pulse-like rupture for the lower-prestress case of $\alpha = 24°$.
值得注意的是,推断出的增强速度减弱参数与 Lu 等人之前的实验研究一致,该研究基于当非线性界面预应力(即解析法向应力与剪切应力之比)减小时,断裂如何从裂纹状转变为脉冲状,从而约束了我们实验界面的稳态速度减弱特性。
自然地震中脉冲式破裂传播模式的起源是地震物理学的一个关键问题。根据预测,闪热导致的速度减弱会在预应力较低的界面上产生脉冲式断裂,这表明这种减弱既能解释滑移脉冲的起源,又能解决热悖论。我们对不断变化的摩擦力的直接测量证实了 Lu 等人的结论,即在他们的实验中观察到的较低二维预应力下的脉冲样断裂是由于摩擦力的速度大幅减弱造成的。事实上,我们的实验在较低预应力($\alpha = 24°$)情况下出现了主要的脉冲样断裂。
To summarize, our experimental measurement demonstrate, for the first time, that friction evolution with slip velocity is consistent with the combined rate-and-state and flash-heating weakening formulation based on measurements performed locally during a spontaneously evolving rupture, rather than from a combination of classical friction experiments where different sliding velocities are imposed from the testing apparatus and assumed to be uniform over the slipping surface. Our measurements on Homalite, a polymer, also suggest the generality of the flash-heating formulation, which was initially proposed in engineering tribology to interpret dry friction in metals, and then studied in earthquake science as a candidate mechanism contributing to friction evolution during seismic slip. Indeed, there is a remarkable qualitative similarity between our measurements obtained on a polymer and those obtained on quartzite rock (Fig. 8a,b).
总之,我们的实验测量结果首次证明,摩擦力随滑动速度的演变与速率-状态和闪热减弱的组合公式是一致的,该公式是基于自发演变的破裂过程中进行的局部测量,而不是来自传统摩擦实验的组合,在传统摩擦实验中,不同的滑动速度是由测试设备施加的,并假定滑动表面上的滑动速度是一致的。我们对高聚物 Homalite 的测量结果也表明了闪热公式的普遍性,闪热公式最初是在工程摩擦学中提出的,用于解释金属中的干摩擦,后来在地震科学中被研究为地震滑动过程中摩擦演变的一种候选机制。事实上,我们在聚合物上获得的测量结果与在石英岩上获得的测量结果在质量上有显著的相似性(图 8a,b)。
On interpreting our experiments with slip-dependent laws
The two experiments presented in Fig. 5a display friction evolution with slip resembling linear slip-weakening friction (equation (11) in Methods). According to linear slip weakening, the dynamic friction coefficient $f_{d}$ and the characteristic slip distance $D_{c}$ are material parameters and, as a consequence, the dependence of friction on slip is the same for a given interface.
Instead, our measurements show that the dependence of friction on slip is different for different slip-rate histories (Fig. 5), indicating that friction cannot be described by a purely slip-dependent law. In the two experiments of Fig. 5a, which appear closest to the linear slip weakening, the apparent dynamic friction coefficient $f_{d}$ and slip weakening distance $D_{c}$ are different, indicating that they are not material properties, but rather effective quantities that depend on the dynamics of the process.
图 5a 中的两个实验显示了摩擦力的演变,其滑移类似于线性滑移减弱摩擦力(方法中的公式 (11))。根据线性滑移减弱,动摩擦系数 $f_{d}$ 和特征滑移距离 $D_{c}$ 是材料参数,因此,对于给定的界面,摩擦对滑移的依赖性是相同的。
相反,我们的测量结果表明,在不同的滑移速率历史条件下,摩擦力对滑移的依赖性是不同的(图 5),这表明摩擦力不能用纯粹的滑移依赖法则来描述。在图 5a 中最接近线性滑移减弱的两个实验中,表观动摩擦系数 $f_{d}$ 和滑移减弱距离 $D_{c}$ 是不同的,这表明它们不是材料属性,而是取决于过程动态的有效量。
Our measurements indicate that the slip scale over which friction decreases depends on the slip-rate history but not directly on the level of normal stress, in contrast with what inferred by other authors. If such slip scale depended on the normal stress, two measurements performed under the same level of normal prestress $\sigma_{0}$, but different slip-rate histories, would exhibit the same slip scale. Our tests show that this is not the case, as illustrated by the following two examples.
In the case with a pulse-like rupture followed by the supershear crack-like rupture ($P = 12\text{ MPa}$ and $\alpha = 24°$, Figs 4c and 5b,d), the slip over which weakening occurs is significantly different between the initial pulse-like and the following crack-like parts of the rupture, despite the normal stress being the same. Another example is provided by a test with an applied far-field loading $P = 13.6\text{ MPa}$ and inclination angle $\alpha = 29°$, which has the same value of the resolved normal stress on the interface, $\sigma_{0} = P \cos^{2}{\alpha}= 10\text{ MPa}$, as the test at $P = 12\text{ MPa}$ and $\alpha = 24°$. While these two tests are conducted under the same level of interface-normal stress, they have substantially different slip rate histories (Fig. 5d), evolution of friction with slip (Fig. 5b), and slip scale over which friction decreases (Fig. 5b).
我们的测量结果表明,摩擦力减小的滑移尺度取决于滑移速率历史,而不是直接取决于法向应力水平,这与其他学者的推断不同。如果这种滑移尺度取决于法向应力,那么在法向预应力 $\sigma_{0}$ 水平相同但滑移速率历史不同的情况下进行的两次测量就会显示出相同的滑移尺度。我们的测试表明情况并非如此,下面两个例子可以说明这一点。
在脉冲样断裂后出现过剪切裂纹样断裂的情况下($P = 12\text{ MPa}$ 和 $\alpha = 24°$,图 4c 和 5b,d),尽管法向应力相同,但最初的脉冲样断裂和随后的裂纹样断裂部分发生削弱的滑移显著不同。另一个例子是应用远场加载 $P = 13.6\text{ MPa}$ 和倾角 $\alpha = 29°$ 的试验,该试验与在 $P = 12\text{ MPa}$ 和 $\alpha = 24°$ 条件下的试验具有相同的界面解析法向应力值,即 $\sigma_{0} = P \cos^{2}{\alpha}= 10\text{ MPa}$ 。虽然这两个测试是在相同的界面法向应力水平下进行的,但它们的滑移率历史(图 5d)、摩擦力随滑移的演变(图 5b)以及摩擦力随之减小的滑移尺度(图 5b)却大不相同。
We conclude that both the slip-weakening length scale and the (variable) dynamic level of friction depend on the slip-rate history, and hence the linear slip-weakening friction law is not an adequate description of friction evolution.
我们的结论是,滑移减弱的长度尺度和摩擦力的(可变)动态水平都取决于滑移速率的历史,因此线性滑移减弱摩擦力定律并不能充分描述摩擦力的演变。
On interpreting our experiments with flash heating
The weakening velocity $V_{w}$ in the flash heating process for our Homalite interface can be estimated as
$$ \begin{equation} \begin{aligned} V_{w} &= \left(\frac{\pi\alpha_{\text{th}}}{D_{A}}\right)\left[\frac{\rho c_{p}}{\tau_{c}}(T_{w} - T_{f})\right]^{2}\\ &= \left(\frac{\pi\times 3.61\times 10^{-8}}{m\times 10^{-6}}\right)\left[\frac{1230\times 1.13\times 10^3\times n\times 100}{195\times 10^6}\right]^2 = 0.27\times \frac{n^{2}}{m} \end{aligned}\tag{2} \end{equation} $$
where $\alpha_{\text{th}} = 3.61\times 10^{-18}\text{ m}^{2}\text{s}^{-1}$ is thermal diffusivity, $\rho c_{p} = 1.39\times 10^{6}\text{ J m}^{-3}\text{ K}^{-1}$ is heat capacity per unit volume, $D_{a} = m\mu\text{m}$ is the avarage contact diameter(with $m = 1-10$), $\tau_{c} = 0.1\mu = 196\text{ MPa}$ is the shear strength of the contact(estimated as one tenth of the shear modulus of the bulk), and $T_{w} - T_{f} = n\times 10^{2}\text{ K}$ is the temperature change that activates flash heating, which could be several hundred degrees for Homalite.
Homalite 界面闪热过程中的削弱速度 $V_{w}$ 可估算为
$$ \begin{equation} \begin{aligned} V_{w} &= \left(\frac{\pi\alpha_{\text{th}}}{D_{A}}\right)\left[\frac{\rho c_{p}}{\tau_{c}}(T_{w} - T_{f})\right]^{2}\\ &= \left(\frac{\pi\times 3.61\times 10^{-8}}{m\times 10^{-6}}\right)\left[\frac{1230\times 1.13\times 10^3\times n\times 100}{195\times 10^6}\right]^2 = 0.27\times \frac{n^{2}}{m} \end{aligned}\tag{2} \end{equation} $$
其中,$\alpha_{\text{th}} = 3.61\times 10^{-18}\text{ m}^{2}\text{s}^{-1}$ 是热扩散率,$\rho c_{p} = 1.39 \times 10^{6}\text{ J m}^{-3}\text{ K}^{-1}$ 是单位体积的热容量,$D_{a} = m\mu\text{m}$ 是平均接触直径($m = 1-10$),$\tau_{c} = 0.1\mu = 196\text{ MPa}$ 是接触点的剪切强度(估计为块体剪切模量的十分之一),$T_{w} - T_{f} = n\times 10^{2}\text{ K}$ 是激活闪热的温度变化,对于高铝酸盐材料来说可能高达几百度。
Given that $m = 1–10$ and $n = 1–3$, the weakening velocity $V_{w}$ is estimated to be of the order of $0.1$ to $1\text{ m s}^{1}$. Note that this estimate is uncertain, since even the assumed values of the thermal diffusivity, heat capacity and shear contact strength may be different for the specific Homalite used in our study.
考虑到 $m = 1-10$ 和 $n = 1-3$,弱化速度 $V_{w}$ 估计在 $0.1$ 到 $1\text{ m s}^{1}$ 之间。请注意,这一估计值是不确定的,因为对于我们研究中使用的高铝土,即使是热扩散率、热容量和剪切接触强度的假定值也可能不同。
For the combined formulation of rate-and-state friction supplemented with flash heating (equation (18)), the leastsquares fit of our steady-state friction measurements (Fig. 8a) leads to $V_{w}{(1)} = 1.10\text{ m s}^{-1}$ and $f_{w}^{(c)} = 0.27$. This fitted value of the characteristic weakening velocity is broadly consistent with the estimate above for reasonable $n$ and $m$ values, for example, $n = 2$ and $m = 1$. The thermal properties of Homalite need to be known in greater detail to provide a more constrained comparison that could indirectly substantiate the flash heating explanation for weakening.
对于速率-状态摩擦辅以闪热的组合公式(等式 (18)),我们的稳态摩擦测量(图 8a)的最小二乘法得出 $V_{w}{(1)} = 1.10\text{ m s}^{-1}$ 和 $f_{w}^{(c)} = 0.27$。对于合理的 $n$ 和 $m$ 值,例如 $n = 2$ 和 $m = 1$,特征弱化速度的这一修正值与上述估计值基本一致。我们需要更详细地了解 Homalite 的热特性,以提供更有约束性的比较,从而间接证实闪热对弱化的解释。
It is not possible to observe flash heating directly in our experiments due to a number of experimental and technological limitations. Flash heating happens when tips of asperities (which are of the order of $1\text{ mm}$) quickly heat up during contact and then cool down when not in contact. This highly transient heating over micrometer scale cannot be detected with available experimental diagnostics and leaves no post-mortem signature. That is why we conclude that the experimental measurements are consistent with the flash-heating formulation, but we cannot conclusively claim that flash heating actually occurs in our experiments.
由于实验和技术方面的限制,我们无法在实验中直接观察到闪热现象。闪热发生时,针尖(数量级为 $1\text{ mm}$)会在接触过程中迅速升温,然后在不接触时冷却下来。这种微米级的高瞬态加热无法用现有的实验诊断方法检测到,也不会在消失后留下任何特征。这就是为什么我们得出结论认为实验测量结果与闪热理论一致,但我们不能断言闪热在我们的实验中确实发生了。
Discussion
Our findings conclusively demonstrate that, during spontaneously evolving dynamic rupture, friction has complex evolution with substantial velocity weakening at high, seismic slip rates. Consequently, purely slip-dependent friction formulations cannot capture the evolution of dynamic friction. At the same time, friction is not purely rate-dependent.
At the high slip rates tested in our study, standard, logarithmic rate-and-state friction models can predict the initial strengthening behaviour but not the substantial weakening that follows. The steady-state friction behaviour at high slip rates can be captured with the formulation developed for enhanced weakening due to flash heating, which appears to be valid for a wide range of materials, including metals, rocks, and, as shown in this work, polymers. This points towards universality of dynamic friction and makes our measurements relevant to many engineering and materials science applications involving friction, such as composite materials failure by fibre pull-out.
我们的研究结果最终证明,在自发演化的动态断裂过程中,摩擦力的演化非常复杂,在高地震滑移率的情况下,摩擦力的速度会大幅减弱。因此,纯粹依赖滑动的摩擦公式无法捕捉动态摩擦的演变。同时,摩擦力也并非纯粹取决于速率。
在我们的研究中测试的高滑移率下,标准的对数速率-状态摩擦模型可以预测最初的强化行为,但无法预测随后的大幅削弱。高滑移率下的稳态摩擦行为可通过为闪热导致的增强削弱而开发的公式来捕捉,该公式似乎适用于多种材料,包括金属、岩石以及本研究中所示的聚合物。这表明了动态摩擦的普遍性,并使我们的测量结果与许多涉及摩擦的工程和材料科学应用相关,如纤维拉出导致的复合材料失效。
Our results have important implications for earthquake physics, validating approaches in which experimental results for simplified slip and slip-velocity histories are combined to study the overall dynamic rupture behaviour. Furthermore, the substantial weakening observed at seismic slip rates in the laboratory is likely to operate during natural earthquakes and could explain the lack of heat flow observed on some active faults, such as the San Andreas Fault.
At the same time, friction on natural faults can be affected by a number of additional factors that are not accounted for in our present laboratory set-up, including the presence of fault gouge, pore fluids and off-fault damage. The novel experimental approach to dynamic friction measurements developed in this work can be used to study the effects of some of these factors on dynamic friction, by intro- ducing damage in the bulk, adding rock gouge to the specimen interface, and inducing multiple ruptures in the same specimen.
我们的研究结果对地震物理学具有重要意义,验证了将简化滑移和滑移速度历史的实验结果结合起来研究整体动态破裂行为的方法。此外,在实验室中观察到的地震滑移率下的大幅减弱很可能在自然地震中发生,这也可以解释在圣安德烈亚斯断层等一些活动断层上观察到的热流缺乏现象。
同时,天然断层上的摩擦力还可能受到一些额外因素的影响,而这些因素在我们目前的实验室设置中并没有考虑到,其中包括断层破碎带、孔隙流体和断层外损伤的存在。本研究开发的动态摩擦力测量新实验方法可用于研究上述因素对动态摩擦力的影响,具体方法包括在主体中引入损伤、在试样界面中加入岩隙以及在同一试样中诱发多次破裂。
Methods
Laboratory earthquake set-up
The laboratory earthquake set-up mimics a fault in the Earth’s crust loaded in compression and shear by the frictionally held interface of two Homalite quadrilateral plates. A square plate of Homalite-100, with the dimensions $200\text{ mm} \times 200\text{ mm}\times 10\text{ mm}$, is cut using computer-numericalcontrol (CNC) milling, producing an interface of inclination angle $\alpha$ (Fig. 1). The mating surfaces of the interface are subsequently polished to a near-optical grade finish, in order to erase any manufacturing marks coming from the computer-numerical-control cutting.
实验室地震装置模拟地壳中的断层,由两块 Homalite 四边形板的摩擦界面加载压缩和剪切力。一块 Homalite-100 的正方形板,尺寸为 $200\text{ mm}$ 用计算机数控(CNC)铣床切割,产生一个倾斜角为 $\alpha$ 的界面(图 1)。接口的配合面随后被抛光到接近光学级的光洁度,以消除计算机数控切割产生的任何制造痕迹。
The surfaces are then roughened by employing a micro-bead blasting procedure with abrasive glass media having diameters in the range of $104–211\text{ mm}$ (refs 30,32). This protocol ensures consistent surface roughness and repeatability of the dynamic frictional rupture experiments. New test specimens are used in every test. The two Homalite quadrilateral plates are brought into contact and compressed with a uniaxial load $P$ (Fig. 1).
然后使用直径在 $104–211\text{ mm}$ 范围内的玻璃研磨介质进行微珠喷射,使表面粗化(参考文献 30、32)。这种方法确保了表面粗糙度的一致性和动态摩擦破裂实验的可重复性。每次试验都使用新的试样。将两块 Homalite 四边形板接触并用单轴负载 $P$ 压缩(图 1)。
The applied loading $P$, in conjunction with the inclination angle $\alpha$, control the level of shear $\tau_{0} = P \sin{\alpha}\cos{\alpha}$ and normal $\sigma_{0} = P\cos^{2}{\alpha}$ prestress on the fault. The non-dimensional prestress is given by $\tau_{0}/\sigma_{0} = \tan{\alpha}$. Nucleation of dynamic rupture is obtained through a local pressure release provided by a rapid expansion of a NiCr wire filament due to an electrical discharge.
外加荷载 $P$ 与倾角 $\alpha$ 共同控制着断层上的剪应力 $\tau_{0} = P \sin{\alpha}\cos{\alpha}$ 和法向预应力 $\sigma_{0} = P\cos^{2}{\alpha}$ 的水平。无量纲预应力由 $\tau_{0}/\sigma_{0} = \tan{\alpha}$ 给出。动态断裂的成核是通过镍铬丝在放电过程中快速膨胀所产生的局部压力释放来实现的。
To provide a characteristic texture for image matching, the specimen’s surface is first coated with a uniform layer of white paint and then decorated with a random black-speckle pattern. To resolve sharp displacement gradients, a small speckle size is required. On the other hand, too small speckles would result in aliasing. This results in an average desired speckle size of $3–6$ pixels. Since we image areas of different dimensions, the speckle size is adapted to each case to be consistently in the range of 3–6 pixels. An example of speckled images is provided in Fig. 1.
为了提供图像匹配所需的特征纹理,首先在试样表面涂上一层均匀的白色油漆,然后用随机的黑色斑点图案进行装饰。为了分辨尖锐的位移梯度,需要较小的斑点尺寸。另一方面,太小的斑点会导致混叠。因此,平均所需的斑点尺寸为 $3-6$ 像素。由于我们要对不同尺寸的区域进行成像,因此斑点大小要根据具体情况进行调整,使其始终保持在 $3-6$ 像素的范围内。图 1 是斑点图像的一个示例。
The high-speed diagnostics consists of an ultrahigh-speed camera system, capable of up to 10 million frames per s, a high-voltage pulse generator to discharge the NiCr wire and initiate the rupture, and a high-speed white light source system (Fig. 2). A sequence of 128 digital images of the specimen during rupture propagation is acquired using a Shimadzu HPV-X camera, at 1 to 2 million frames per s, depending on the experiment, and with a resolution of $250\times 400$ pixels.
The images discussed in this work are taken over an area ranging from a minimum of $18\times 11.2\text{ mm}^{2}$, which are typically recorded at 2 million frames per s, up to $145\times 91\text{ mm}^{2}$, recorded at 1 million frame per s. In addition, for selected experiments, laser heterodyne interferometers are employed to accurately measure particle velocities at up to two locations in one experiment.
高速诊断系统包括一个超高速摄像系统(每秒可拍摄 1000 万帧)、一个用于镍铬丝放电并引发断裂的高压脉冲发生器和一个高速白光光源系统(图 2)。使用岛津 HPV-X 相机以每秒 100 万至 200 万帧的速度(视实验而定)获取断裂传播过程中试样的 128 幅数字图像序列,分辨率为 $250 × 400$ 像素。
这项工作中讨论的图像的拍摄区域范围最小为 $18\times 11.2\text{ mm}^{2}$(通常以每秒200万帧的速度记录),最大为 $145\times 91\text{ mm}^{2}$(以每秒100万帧的速度记录)。此外,在选定的实验中,还采用了激光外差干涉仪来精确测量一次实验中至多两个位置的粒子速度。
Full-field imaging of dynamic ruptures
In order to produce a full-field characterization of the dynamic ruptures, we employ the digital image correlation method (DIC). The DIC method is an optical technique, which analyses digital images by tracking, with sub-pixel accuracy, the motion and deformations of image windows containing a characteristic grey-level signature. We use the correlation software VIC-2D (Correlation Solutions Inc.) enhanced with the ‘Fill-Boundary’ algorithm to treat interface discontinuities. The correlation analysis is performed by comparing the specimen’s image, taken before rupture, to each subsequent deformed image. The displacement fields are then computed with respect to the chosen reference configuration.
为了获得动态断裂的全场特征,我们采用了数字图像相关方法(DIC)。DIC 方法是一种光学技术,通过以亚像素精度跟踪包含灰度特征的图像窗口的运动和变形来分析数字图像。我们使用关联软件 VIC-2D(Correlation Solutions Inc.)相关分析是通过比较破裂前的试样图像和随后的变形图像来进行的。然后根据所选的参考配置计算位移场。
Two key parameters in performing the correlation analysis are the subset size and step size. Pattern matching is performed over image subsets to regularize the non-uniqueness of the pixel-by-pixel correlation problem. The subset size is the size of the image window whose motion and deformation is tracked by the correlation algorithm. For each subset, the solution provides the two in-plane displacement components at the subset center.
进行相关性分析的两个关键参数是子集大小和步长。对图像子集进行模式匹配是为了规范逐像素相关性问题的非唯一性。子集大小是图像窗口的大小,相关算法跟踪其运动和变形。对于每个子集,解决方案提供子集中心的两个平面内位移分量。
Smaller subset sizes result in finer spatial resolution, while too small subsets do not contain enough gray-level information and result in larger errors. The subset size choice also depends on the signal-to-noise ratio (SNR); tests with larger SNR can afford smaller subset sizes. The step size is the distance between the centers of two nearest subsets. Smaller step sizes increase the density of correlation results. For example, the two tests presented in Fig. 4a,b were analysed with a subset size of $41$ pixels ($1.9\text{ mm}$) and $51$ pixels ($2.3\text{ mm}$) for the case of larger ($P = 23\text{ MPa}$) and smaller applied loading ($P = 7.4\text{ MPa}$) respectively. The step size was $1$ pixel ($46\text{ mm}$) for both cases.
子集尺寸越小,空间分辨率越精细,而太小的子集则不包含足够的灰度级信息,导致误差增大。子集大小的选择还取决于信噪比(SNR);信噪比越大的测试,子集大小越小。步长是两个最近子集中心之间的距离。步长越小,相关结果的密度越高。例如,对图 4a,b 中的两个测试进行分析时,分别使用了 $41$ 个像素($1.9\text{ mm}$)和 $51$ 个像素($2.3\text{ mm}$)的子集大小来处理较大($P = 23\text{ MPa}$)和较小($P = 7.4\text{ MPa}$)的应用载荷。两种情况下的步长均为 $1$ 像素($46\text{ mm}$)。
The images are correlated over two independent rectangular domains, separated at the specimen interface. This is because employing one domain containing the interface would imply using subsets across the interface, averaging displacements on the opposite sides of the interface and preventing us from capturing the discontinuities across the interface.
图像在两个独立的矩形域上相关联,在试样界面处分开。这是因为如果使用一个包含界面的域,就意味着要使用界面两侧的子集,平均界面两侧的位移,从而无法捕捉界面两侧的不连续性。
Since the correlation solution is found for the subset center, the standard VIC-2D algorithm would only be able to produce the displacement map up to half a subset away from the interface. The ‘Fill-Boundary’ algorithm, developed by Correlated Solutions Inc. with our input, uses affine transform functions to extrapolate the displacements all the way to the interface.
由于相关解是针对子集中心找到的,因此标准的 VIC-2D 算法只能绘制出距离界面最远半个子集的位移图。根据我们的输入, Correlated Solutions 公司开发的 “填充边界” 算法使用仿射变换函数将位移一直推广到界面。
Post-processing of the displacement fields
Displacement fields are filtered with the non-local-means (NL-means) filter. In contrast with local filters, which smooth each pixel with neighboring pixels regardless of their content and are not capable of capturing discontinuities, the NL-means filter accounts for the ‘context’ around each pixel. This is achieved by considering windows (neighbourhoods) around each pixel and comparing them to neighboring windows. The windows are then averaged with Gaussian weights, where larger weights are assigned to windows that express a higher degree of similarity.
位移场采用非局部均值(NL-means)滤波器进行过滤。局部滤波器会将每个像素与邻近像素进行平滑处理,而不考虑其内容,也无法捕捉不连续性,与之相比,非局部均值滤波器会考虑每个像素周围的 “环境”。具体做法是考虑每个像素周围的窗口(邻域),并将其与邻近窗口进行比较。然后用高斯权重对这些窗口进行平均,将较大的权重分配给相似度较高的窗口。
This procedure enables efficient image denoising, preserving sharp features and large gradients. The NL-means filter operates with the following input parameters: the size of the neighborhood $N$, the search area dimension $\Omega$, which defines the span over which the search of similar neighbourhoods is computed, and the noise parameter h, related to noise level of the signal. In all cases analysed in this study, we use: $N = 3\times 3$ pixels, $\Omega = 21\times 21$ pixels, and $h = 0.5$. We found that a second iteration of the NL-means filter with the same parameters helped to further smooth the displacement fields without lost of information. We have also investigated and checked the effect of filtering parameters both on the displacement and strain fields. The above reported parameters achieve displacement smoothing yet maintaining intact the original signal pattern. An example of the sequence of two images is shown in Fig. 1.
该程序可实现高效的图像去噪,保留清晰的特征和较大的梯度。NL-means 过滤器使用以下输入参数进行操作:邻域大小 $N$、搜索区域维度 $\Omega$(定义了计算搜索相似邻域的跨度)以及与信号噪声水平相关的噪声参数 h。在本研究分析的所有案例中,我们使用:$N = 3\times 3$ 像素,$\Omega = 21\times 21$ 像素,以及 $h = 0.5$。我们发现,使用相同参数的 NL-means 过滤器的第二次迭代有助于在不丢失信息的情况下进一步平滑位移场。我们还研究并检验了滤波参数对位移场和应变场的影响。上述报告的参数在实现位移平滑的同时,保持了原始信号模式的完整。图 1 是两个图像序列的示例。
Strains are computed from the filtered displacement fields using the finite difference approximation. Away from the boundaries, we use the central difference scheme:
$$ \begin{align} \epsilon_{11}(i,j,k) &= \frac{u_{1}(i,j+h_{s},k) - u_{1}(i,j - h_{s}, k)}{2h_{s}sp}\tag{3}\\ \epsilon_{22}(i,j,k) &= - \frac{u_{2}(i+h_{s},j,k) - u_{2}(i - h_{s},j,k)}{2h_{s}sp}\tag{4}\\ \epsilon_{12}(i,j,k) &= \frac{1}{2}\left\{- \frac{u_{1}(i+h_{s},j,k) - u_{1}(i - h_{s},j,k)}{2h_{s}sp} + \frac{u_{2}(i,j+h_{s},k) - u_{2}(i,j - h_{s}, k)}{2h_{s}sp}\right\}\tag{5} \end{align} $$
where $u_{1}(i,j,k)$ and $u_{2}(i,j,k)$ are the fault-parallel and fault-normal displacement components, respectively (Fig. 1c shows the fault-parallel component), for pixel $(i, j)$ and frame $k$, expressed in mm; $2h_{s}$ defines the stencil size and $s$ is the step size, both expressed in pixels; $p$ is the pixel size, which for the two cases presented in the main text is $46\text{ mm}$. Here we take $h_{s} = 1\text{ pixel}$. Close to the interface, we use the backward or forward difference scheme to compute strains above and below the interface, respectively. Below the interface, the forward difference approximation reads:
$$ \begin{align} \epsilon_{11}(i,j,k) &= \frac{-u_{1}(i,j + 2h_{s},k) + 4u_{1}(i,j + h_{s},k) - 3u_{1}(i,j,k)}{2h_{s}sp}\tag{6}\\ \epsilon_{22}(i,j,k) &= -\frac{-u_{2}(i + 2h_{s},j,k) + 4u_{2}(i + h_{s},j,k) - 3u_{2}(i,j,k)}{2h_{s}sp}\tag{7}\\ \epsilon_{12}(i,j,k) &= \frac{1}{2}\left\{-\frac{u_{1}(i + 2h_{s},j,k) + 4u_{1}(i + h_{s},j,k) - 3u_{1}(i,j,k)}{2h_{s}sp} \right.\\ &+\left.\frac{-u_{2}(i,j+2h_{s},k) + 4u_{2}(i,j+h_{s},k) - 3u_{2}(i,j,k)}{2h_{s}sp}\right\}\tag{8} \end{align} $$
根据过滤后的位移场,采用有限差分近似法计算应变。在远离边界的地方,我们使用中心差分方案:
$$ \begin{align} \epsilon_{11}(i,j,k) &= \frac{u_{1}(i,j+h_{s},k) - u_{1}(i,j - h_{s}, k)}{2h_{s}sp}\tag{3}\\ \epsilon_{22}(i,j,k) &= - \frac{u_{2}(i+h_{s},j,k) - u_{2}(i - h_{s},j,k)}{2h_{s}sp}\tag{4}\\ \epsilon_{12}(i,j,k) &= \frac{1}{2}\left\{- \frac{u_{1}(i+h_{s},j,k) - u_{1}(i - h_{s},j,k)}{2h_{s}sp} + \frac{u_{2}(i,j+h_{s},k) - u_{2}(i,j - h_{s}, k)}{2h_{s}sp}\right\}\tag{5} \end{align} $$
其中,$u_{1}(i,j,k)$ 和 $u_{2}(i,j,k)$ 分别是像素 $(i, j)$ 和帧 $k$ 的断层平行和断层法向位移分量(图 1c 显示了断层平行分量),单位为毫米;$2h_{s}$ 定义了模板大小,$s$ 是步长,两者都以像素为单位;$p$ 是像素大小,对于正文中提到的两种情况,其值为 $46\text{ mm}$。这里取 $h_{s} = 1\text{ pixel}$。接近界面时,我们使用向前或向后差分方案分别计算界面上方和下方的应变。在界面下方,向前差分近似为:
$$ \begin{align} \epsilon_{11}(i,j,k) &= \frac{-u_{1}(i,j + 2h_{s},k) + 4u_{1}(i,j + h_{s},k) - 3u_{1}(i,j,k)}{2h_{s}sp}\tag{6}\\ \epsilon_{22}(i,j,k) &= -\frac{-u_{2}(i + 2h_{s},j,k) + 4u_{2}(i + h_{s},j,k) - 3u_{2}(i,j,k)}{2h_{s}sp}\tag{7}\\ \epsilon_{12}(i,j,k) &= \frac{1}{2}\left\{-\frac{u_{1}(i + 2h_{s},j,k) + 4u_{1}(i + h_{s},j,k) - 3u_{1}(i,j,k)}{2h_{s}sp} \right.\\ &+\left.\frac{-u_{2}(i,j+2h_{s},k) + 4u_{2}(i,j+h_{s},k) - 3u_{2}(i,j,k)}{2h_{s}sp}\right\}\tag{8} \end{align} $$
Stress fields are computed from strain fields using the standard plane-stress linear elastic constitutive equations (Fig. 1e shows the shear stress component). Since Homalite is a viscoelastic material, we use the dynamic Young’s modulus $E_{d} = 5.3\text{ GPa}$ (ref. 46) to compute the dynamic stress change, together with a Poisson’s ratio of $\nu = 0.35$ (refs 32,49). Since the displacement fields are computed using the loaded specimen configuration as reference, the strains and stresses computed from these fields are changes over the reference configuration. To recover the actual level of stress, we add the computed resolved normal and shear stress, in the reference configuration, to the DIC measured stresses as:
$$ \begin{align} \sigma_{\text{actual}} &= \sigma_{0} + \Delta \sigma_{\text{DIC}}\tag{9}\\ \tau_{\text{actual}} &= \tau_{0} + \Delta \tau_{\text{DIC}}\tag{10} \end{align} $$
应力场是利用标准平面应力线性弹性构成方程从应变场计算得出的(图 1e 显示的是剪应力分量)。由于 Homalite 是一种粘弹性材料,我们使用动态杨氏模量 $E_{d} = 5.3\text{ GPa}$(参考文献 46)来计算动态应力变化,同时使用泊松比 $\nu = 0.35$(参考文献 32、49)。由于位移场是以加载试样的配置为参考计算的,因此根据这些场计算出的应变和应力是参考配置的变化。为了恢复实际的应力水平,我们将计算出的参考构型下的解析法向应力和剪切应力与 DIC 测量应力相加,计算公式为
$$ \begin{align} \sigma_{\text{actual}} &= \sigma_{0} + \Delta \sigma_{\text{DIC}}\tag{9}\\ \tau_{\text{actual}} &= \tau_{0} + \Delta \tau_{\text{DIC}}\tag{10} \end{align} $$
This procedure is justified by the fact that the resolved levels of shear and normal stress are nearly uniform along the interface, as discussed in the main text. The particle velocity maps (Fig. 1d) are obtained through time differentiation of the displacement fields (Fig. 1c), using the central difference scheme. The slip and slip rate values are computed by subtracting the displacement and particle velocity values, respectively, at the pixels immediately above and below the interface. The friction coefficient is computed by the shear to normal stress ratio at the pixels along the interface.
正如正文中所讨论的那样,沿界面的剪切应力和法向应力的分辨水平几乎是均匀的,因此这一程序是合理的。粒子速度图(图 1d)是通过对位移场(图 1c)进行时间微分,采用中心差分方案得到的。通过分别减去界面上方和下方像素点的位移和粒子速度值,计算出滑移和滑移率值。摩擦系数由界面沿线像素的剪切应力与法向应力之比计算得出。
Averaging procedure
The slip, slip rate, traction components and friction values are initially computed for all pixels along the interface. To produce the time histories and friction evolution curves presented here, we average the slip, slip rate, and stress components over a 1 mm region at the center of the imaged area, which is at a distance of 82 mm from the rupture nucleation location.
This procedure reduces potential numerical oscillations of the correlation solution. The averaging of the time histories is achieved by time shifting each curve by $\Delta t = (x_{1} - x_{c}) / V_{r}$, where $V_{r}$ is the rupture speed, $x_{1}$ denotes a generic location and $x_{c}$ denotes the center of the imaged area. The time histories corresponding to locations around the center of the imaged areas are collapsed over the time history corresponding to the center of the field of view, and the curves thus obtained are subsequently averaged.
滑移、滑移率、牵引力分量和摩擦力值最初是为界面上的所有像素计算的。为了生成时间历程和摩擦力演变曲线,我们在成像区域中心 1 毫米的区域内平均计算滑移、滑移率和应力分量,该区域距离断裂成核位置 82 毫米。
这一过程减少了相关解的潜在数值振荡。时间历史的平均化是通过每条曲线的时间移动 $\Delta t = (x_{1} - x_{c}) / V_{r}$ 来实现的,其中 $V_{r}$ 是断裂速度,$x_{1}$ 表示一般位置,$x_{c}$ 表示成像区域的中心。将成像区域中心周围位置对应的时间历程与视场中心对应的时间历程相叠加,然后对由此得到的曲线求平均值。
For the tests discussed in the main text, the averaging over 1 mm involves 22 curves. This procedure is performed for all time histories of interest and it is used to produce the time histories of Fig. 4, the friction versus slip curves of Fig. 5a,b, and the friction versus slip rate curves of Fig. 6. Averaging time histories over 2 and 4 mm regions produces the same results as those obtained with 1 mm averaging, showing both that the signals are already well smoothed and that the rupture is well developed, propagating in a steady fashion. Note that the comparison of slip rate histories at different locations presented in Fig. 7 is performed on curves averaged over a 1 mm region, according to the procedure outlined above.
对于正文中讨论的测试,1 毫米的平均值涉及 22 条曲线。这一过程适用于所有相关的时间历程,并用于生成图 4 的时间历程、图 5a,b 的摩擦力与滑移曲线以及图 6 的摩擦力与滑移率曲线。对 2 毫米和 4 毫米区域的时间历程进行平均后,得到的结果与对 1 毫米区域进行平均后得到的结果相同,这表明信号已经得到很好的平滑处理,而且断裂发展良好,以稳定的方式传播。请注意,图 7 中不同位置滑移率历史记录的比较是根据上述程序,在 1 毫米区域的平均曲线上进行的。
Steady-state friction analysis
In this section, we detail the procedure used to determine the steady-state friction coefficients and steady-state slip rate data points of Fig. 8a. To find steady state values, we select windows of sustained near-constant slip rate, with the slip rate variation, $\Delta V$, satisfying $\Delta V\leq \Delta V_{0}^{\text{max}}$ over the entire window. $\Delta V_{0}^{\text{max}}$ is the maximum variation in slip rate measured before rupture arrival; since that slip rate should be physically zero, $\Delta V_{0}^{\text{max}}$ gives an estimate of the measurement error.
在本节中,我们将详细介绍用于确定图 8a 的稳态摩擦系数和稳态滑移率数据点的程序。为了确定稳态值,我们选择了滑移率持续接近恒定的窗口,滑移率变化($\Delta V$)在整个窗口中满足 $\Delta V\leq \Delta V_{0}^{\text{max}}$ 是在断裂到来之前测量到的最大滑移率变化;由于该滑移率在物理上应该为零,因此 $\Delta V_{0}^{\text{max}}$ 给出了测量误差的估计值。
For the near-constant slip rate to be sustained, the window should contain a minimum number of data points $n_{dp}$. The minimum number of data points guarantees that the steady state is maintained over a minimum time interval before slip rate starts evolving again. We use $n_{dp} = 10$. Note that our time histories are made of 128 data points, corresponding to the recorded camera frames.
要维持近乎恒定的滑移率,窗口应包含最小数量的数据点 $n_{dp}$。最小数据点数可保证在滑移率重新开始演变之前的最小时间间隔内保持稳定状态。我们使用 $n_{dp} = 10$。请注意,我们的时间历程由 128 个数据点组成,与记录的摄像机帧相对应。
The steady state results presented in Fig. 8a comprise four tests performed with the same field of view: $18\text{ mm} \times 11.2\text{ mm}$ (solid symbols in Fig. 8a). We also performed additional experiments with larger fields of view. While these experiments provide more insight, they are characterized by a lower signal to noise ratio.
We perform the same steady-state analysis for them as for the other tests and include the corresponding data points in the steady-state friction versus slip rate plot (empty symbols in Fig. 8a). These steady-state measurements have a larger scatter, yet they follow the same trend as determined with the smaller and more accurate set of data points.
图 8a 所示的稳态结果包括以相同视场进行的四次测试:$18\text{ mm}\times 11.2\text{ mm}$ (图 8a 中的实心符号)。我们还用更大的视场进行了其他实验。虽然这些实验提供了更多的视野,但它们的特点是信噪比较低。
我们对它们进行了与其他测试相同的稳态分析,并将相应的数据点纳入稳态摩擦力与滑移率关系图中(图 8a 中的空符号)。这些稳态测量值的分散度较大,但其趋势与"使用更小、更精确的数据点所确定的趋势"相同。
On friction laws
One of the most common formulations of friction is that of slip weakening. The slip-weakening formulation has been introduced by analogy to cohesive-zone models of mode I cracks as well as based on experimental results. A common simple form of the law, the so-called linear slip weakening, prescribes a linear variation of the friction coefficient $f$ from the static value $f_{s}$ according to:
$$ \begin{equation} f = \begin{cases} f_{s} - (f_{s} - f_{d})\frac{\delta}{D_{c}}, & \delta \leq D_{c}\\ f_{d}, & \delta > D_{c}\end{cases}\tag{11} \end{equation} $$
where $f_{d}$ is the dynamic friction coefficient, and $D_{c}$ is the slip over which $f_{d}$ is reached. In this formulation, the parameters $f_{d}$ and $D_{c}$ are material parameters. For a detailed discussion on these parameters, see the section ‘On interpreting our experiments with slip weakening’.
最常见的摩擦公式之一是滑移削弱公式。滑移减弱公式是通过类比模态 I 裂缝的内聚区模型以及根据实验结果引入的。该定律的一个常见简单形式,即所谓的线性滑移削弱,规定了摩擦系数 $f$ 与静态值 $f_{s}$ 之间的线性变化,其依据如下:
$$ \begin{equation} f = \begin{cases} f_{s} - (f_{s} - f_{d})\frac{\delta}{D_{c}}, & \delta \leq D_{c}\\ f_{d}, & \delta > D_{c}\end{cases}\tag{11} \end{equation} $$
其中 $f_{d}$ 是动摩擦系数,$D_{c}$ 是达到 $f_{d}$ 时的滑移量。在此公式中,参数 $f_{d}$ 和 $D_{c}$ 是材料参数。有关这些参数的详细讨论,请参阅 “关于滑移减弱实验的解释” 一节。
In the widely used rate-and-state friction laws, developed for relatively slow slip rates compared to the seismic range, friction depends on the slip rate $V$ and evolving state variable that represents memory effects
$$ \begin{align} f_{ss} &= f_{*} + a\log{\left(\frac{V}{V_{*}}\right)} + b\log{\left(\frac{V_{*}\theta}{L}\right)},\tag{12}\\ \frac{\mathrm{d}\theta}{\mathrm{d}t} &= 1 - \frac{V\theta}{L}\tag{13} \end{align} $$
where $f_{*}$ is the friction coefficient at the reference velocity $V_{*}$, $a$ and $b$ are rate and state parameters, and $L$ is the characteristic slip for the state variable evolution. Several evolution laws for the state variable have been proposed, including the aging law, given above, the slip law and the composite law. In part, rate-and-state friction incorporates a direct strengthening effect in response to rapid slip rate increases, which can potentially explain the initial strengthening in our experiments (Fig. 5a,b). Note that this formulation results in the dependence of friction on slip similar to slip weakening in the case of slip-rate histories characteristic of the rupture front (Fig. 5a). At steady state, the rate-and-state law takes the form:
$$ \begin{equation} f_{ss} = f_{*} + (a - b) \log{\left(\frac{V}{V_{*}}\right)}\tag{14} \end{equation} $$
We plot this expression in Fig. 8a to compare it with our steady state measurements, using $f_{*} = 0.58$, $V_{*} = 1\mu\text{m s}^{-1}$, $(a - b) = 0.005$ reported by Lu. The measurements were obtained for smaller samples with the same interface preparation procedure in velocity-jump experiments.
在广泛使用的速率-状态摩擦定律中,摩擦力取决于滑移速率 $V$ 和代表记忆效应的不断变化的状态变量。
$$ \begin{align} f_{ss} &= f_{*} + a\log{\left(\frac{V}{V_{*}}\right)} + b\log{\left(\frac{V_{*}\theta}{L}\right)},\tag{12}\\ \frac{\mathrm{d}\theta}{\mathrm{d}t} &= 1 - \frac{V\theta}{L}\tag{13} \end{align} $$
其中 $f_{*}$ 是参考速度 $V_{*}$ 处的摩擦系数,$a$ 和 $b$ 是速率和状态参数,$L$ 是状态变量演化的特征滑移。已经提出了几种状态变量的演化定律,包括上述的老化定律、滑移定律和复合定律。在某种程度上,速率-状态摩擦包含了对快速滑移速率增加的直接强化效应,这可能解释了我们实验中的初始强化(图 5a,b)。请注意,这种公式导致摩擦力与滑移的依赖关系类似于滑移减弱,在滑移速率历史记录特征的断裂前沿的情况下(图 5a)。在稳态下,速率-状态定律的形式为:
$$ \begin{equation} f_{ss} = f_{*} + (a - b) \log{\left(\frac{V}{V_{*}}\right)}\tag{14} \end{equation} $$
我们在图 8a 中绘制了这个表达式,以便与我们的稳态测量进行比较,使用 $f_{*} = 0.58$,$V_{*} = 1\mu\text{m s}^{-1}$,$(a - b) = 0.005$,这些数据由 Lu 报告。这些测量是在具有相同界面制备程序的较小样品上进行的速度跃变实验。
Experiments on rocks show that seismic rates ($V > 0.1{ m s}^{-1}$) are characterized by enhanced rate weakening, dramatically reducing the friction coefficient. One weakening mechanisms with extensive theoretical and experimental support is flash heating. According to the flash heating friction law, the friction coefficient evolves as:
$$ \begin{equation} f = \begin{cases} f_{0}, & V < V_{w}\\ f_{w} - (f_{0} - f_{w})\frac{V_{w}}{V}, & V\geq V_{w}\end{cases}\tag{15} \end{equation} $$
with
$$ \begin{equation} V_{w} = \left(\frac{\pi\alpha_{\text{th}}}{D_{a}}\right)\left[\frac{\rho c_{p}}{\tau_{c}}(T_{w} - T_{f})\right]^{2} \end{equation} $$
where $V_{w}$ is the characteristic weakening velocity, $f_{0}$ is the friction coefficient for $V < V_{w}$, $f_{w}$ is the residual friction coefficient, ath is the thermal diffusivity, $D_{a}$ is the average contact diameter, $\rho$ is the density, $c_{p}$ is the heat capacity, $\tau_{c}$ is the shear strength of individual contacts, $T_{w}$ is the characteristic weakening (e.g., melting) temperature, and $T$ is the average temperature of the slip surface. Note that the theoretical estimate of $V_{w} = 0.1\text{ m s}^{-1}$ for rocks matches the experimentally inferred one. Note also that the estimate does not depend on the normal stress. The normal stress dependence of $V_{w}$ has been observed in experiments but in the context of melt-welt formation.
岩石实验表明,地震速率($V > 0.1{ m s}^{-1}$)的特点是增强的速率削弱,大大降低了摩擦系数。一种具有广泛理论和实验支持的削弱机制是闪热。根据闪热摩擦定律,摩擦系数的演化如下:
$$ \begin{equation} f = \begin{cases} f_{0}, & V < V_{w}\\ f_{w} - (f_{0} - f_{w})\frac{V_{w}}{V}, & V\geq V_{w}\end{cases}\tag{15} \end{equation} $$
其中
$$ \begin{equation} V_{w} = \left(\frac{\pi\alpha_{\text{th}}}{D_{a}}\right)\left[\frac{\rho c_{p}}{\tau_{c}}(T_{w} - T_{f})\right]^{2} \end{equation} $$
其中 $V_{w}$ 是特征削弱速度,$f_{0}$ 是 $V < V_{w}$ 时的摩擦系数,$f_{w}$ 是剩余摩擦系数,$\alpha_{\text{th}}$ 是热扩散率,$D_{a}$ 是平均接触直径,$\rho$ 是密度,$c_{p}$ 是热容量,$\tau_{c}$ 是单个接触的剪切强度,$T_{w}$ 是特征削弱(例如,熔化)温度,$T$ 是滑动表面的平均温度。请注意,对于岩石,$V_{w}$ 的理论估计值为 $0.1\text{ m s}^{-1}$ 与实验推断的值相匹配。还要注意,这个估计值不依赖于法向应力。已经在实验中观察到了 $V_{w}$ 的法向应力依赖性,但是在熔融熔池形成的背景下。
One can combine the rate-and-state expressions at the low slip rates and flash heating at the high slip rates by assuming that $f_{0}$ of the flash heating formulation is given by the rate-and-state formulation and replacing $V$ in the flash heating formulations with $L/\theta$, an expression that evolves towards $V$ with slip. The combined formulation reads:
$$ \begin{equation} f = f_{w}^{(c)} + \frac{\left[f_{*} + a\log{\left(\frac{V}{V_{*}}\right)} + b\log{\left(\frac{V_{*}\theta}{L}\right)}\right] - f_{w}^{(c)}}{1 + \frac{L}{\theta V_{w}^{(c)}}} \end{equation} $$
At steady state, the combined friction law takes the form:
$$ \begin{equation} f = f_{w}^{(c)} + \frac{\left[f_{*} + (a - b)\log{\left(\frac{V}{V_{*}}\right)}\right] - f_{w}^{(c)}}{1 + \frac{V}{V_{w}^{(c)}}} \end{equation} $$
where $f_{w}^{(c)}$ and $V_{w}^{(c)}$ are, respectively, the residual friction coefficient and the weakening slip velocity for the combined formulation.
我们可以将低滑移率时的速率-状态表达式和高滑移率时的闪热表达式结合起来,假设闪热表达式中的 $f_{0}$ 是由速率-状态表达式给出的,并用 $L/\theta$ 代替闪热表达式中的 $V$,这个表达式随着滑移向 $V$ 演进。综合公式如下
$$ \begin{equation} f = f_{w}^{(c)} + \frac{\left[f_{*} + a\log{\left(\frac{V}{V_{*}}\right)} + b\log{\left(\frac{V_{*}\theta}{L}\right)}\right] - f_{w}^{(c)}}{1 + \frac{L}{\theta V_{w}^{(c)}}} \end{equation} $$
在稳态下,综合摩擦定律的形式为
$$ \begin{equation} f = f_{w}^{(c)} + \frac{\left[f_{*} + (a - b)\log{\left(\frac{V}{V_{*}}\right)}\right] - f_{w}^{(c)}}{1 + \frac{V}{V_{w}^{(c)}}} \end{equation} $$
其中 $f_{w}^{(c)}$ 和 $V_{w}^{(c)}$ 分别是综合公式的剩余摩擦系数和削弱滑移速度。
Imaging mini-earthquake ruptures with our ultrahigh speed full-field technique
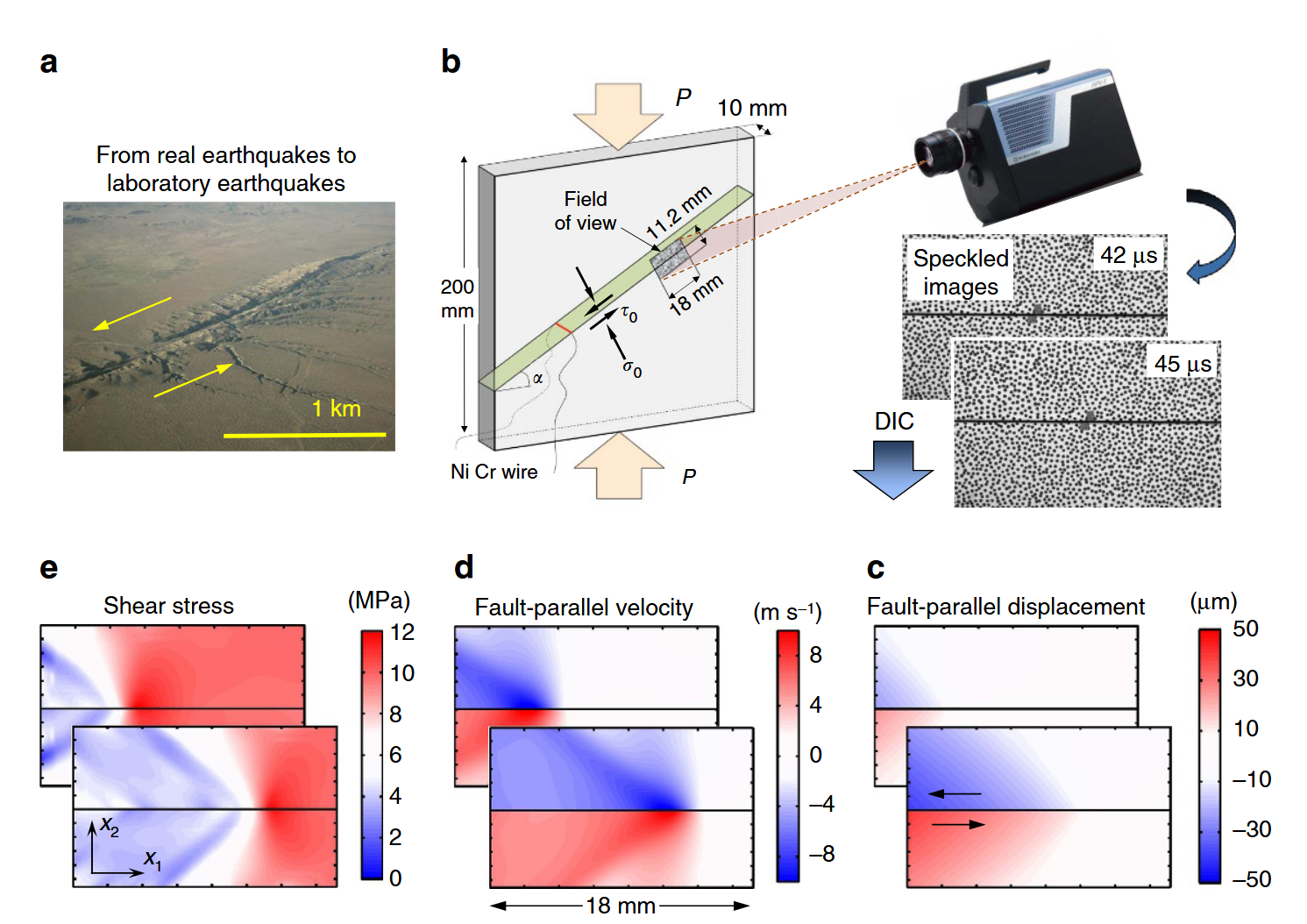
(a,b) Earthquakes are mimicked in the laboratory by dynamic ruptures propagating along an inclined frictional interface, under the applied shear and normal prestresses simulating tectonic loading applied to a fault within the Earth’s crust. The level of prestress is controlled by the applied far-field loading $P$ and interface inclination angle $\alpha$. Part of the interface has a speckled pattern applied for the subsequent analysis. The picture of the San Andreas Fault, shown for visual comparison in a, is modified from www.sanandreasfault.org (Copyright (c) David K. Lynch). (c–e) The full-field time histories of displacements, velocities and stresses are experimentally obtained by capturing sequences of images with ultrahigh speed photography, and processing them with pattern-matching algorithms and highly tailored analysis. The case shown is for $P = 23\text{ MPa}$ and $\alpha = 29°$.
(a,b)在实验室中,地震是通过沿倾斜摩擦界面传播的动态断裂来模拟的,所施加的剪应力和法向预应力模拟了施加在地壳内断层上的构造荷载。预应力水平由施加的远场荷载 $P$ 和界面倾角 $\alpha$ 控制。部分界面上有斑点图案,用于后续分析。a 中用于视觉对比的 San Andreas 断层图片修改自 www.sanandreasfault.org(版权 (c) David K. Lynch)。(c-e) 位移、速度和应力的全场时间历程是通过超高速摄影捕捉图像序列,然后使用模式匹配算法和高度定制的分析方法进行处理而获得的。所示情况为 $P = 23\text{ MPa}$ 和 $\alpha = 29°$。
Laboratory earthquake set-up with the ultrahigh speed digital image correlation and laser velocimeter diagnostics
The sample contains an interface that mimics a crustal fault prestressed both in compression and in shear. Dynamic rupture is triggered through a local pressure release provided by a rapid expansion of a NiCr wire filament due to an electrical discharge. The Shimadzu HPV-X ultrahigh speed camera records images of the specimen during rupture propagation at 1–2 million frames per s. The well-developed technique of laser velocimetry is used for comparison of pointwise velocity measurements obtained with the full-field technique at selected locations.
样品包含一个模拟地壳断层的界面,在压缩和剪切状态下都受到预应力。镍铬丝在放电作用下迅速膨胀,释放局部压力,从而触发动态断裂。岛津 HPV-X 超高速照相机以每秒 100 万至 200 万帧的速度记录断裂传播过程中试样的图像。
Validation of digital image correlation method with laser velocimeters
(a) Schematics of the configuration employed for the comparison of the full-field imaging method to the laser velocimeter technique. The field of view (blue rectangle, $50\times 31\text{ mm}^{2}$) and the location of the velocimeter measurements (P1 and P2) are indicated. (b) Fault-parallel velocity time-histories measured with laser velocimeters (colored curves) and with the full-field DIC technique (black curves). The curve corresponding to the velocimeter location P2 is shifted upwards by $7\text{ m s}^{-1}$ for clarity. Note the excellent agreement of the two measurements. The two black curves based on the full-field technique from above and below the interface show a near-perfect anti-symmetric signal, consistent with in-plane shear rupture.
(a) 用于比较全场成像法和激光测速仪技术的配置示意图。图中标出了视场(蓝色矩形,$50\times 31\text{ mm}^{2}$)和测速仪的测量位置(P1 和 P2)。(b) 利用激光测速仪(彩色曲线)和全场 DIC 技术(黑色曲线)测量的断层平行速度时间历史。为清晰起见,对应于测速仪位置 P2 的曲线向上移动了 $7\text{ m s}^{-1}$。请注意,两次测量结果非常吻合。基于界面上方和下方全场技术的两条黑色曲线显示出近乎完美的反对称信号,与平面内剪切破裂一致。
Monitoring the laboratory earthquake vitals
(a) Slip rate and (b) shear stress time histories obtained on the interface at the center of the field of view shown in Fig. 1 for two far field loads, $P = 23\text{ MPa}$ (blue) and $P = 7.4\text{ MPa}$ (red), and angle $\alpha = 29°$; both cases result in supershear ruptures. Insets: Magnified slip rate and shear stress time histories for the case $P = 7.4\text{ MPa}$. The rupture produced by the higher far-field load has an order of magnitude higher peak slip rate and a more prominent reduction in shear stress compared to the lower load case. Yet the two ruptures are qualitatively similar as demonstrated by the insets. (c) Slip rate and (d) shear stress time histories for $P = 12\text{ MPa}$ and $\alpha = 24°$. This experiment has a very different slip-rate history, with a sub-Rayleigh pulse-like rupture propagating first, followed by a reflected supershear crack-like rupture.
(a) 图 1 所示视场中心界面上的滑移率和 (b) 两种远场载荷($P = 23\text{ MPa}$(蓝色)和 $P=7.4\text{ MPa}$(红色)以及角度 $\alpha = 29°$)下的剪应力时间历程;这两种情况都会导致超剪切断裂。插图:$P = 7.4\text{ MPa}$ 情况下放大的滑移率和剪应力时间历程。与较低载荷情况相比,较高远场载荷产生的断裂具有更高的峰值滑移率和更显著的剪切应力减小。然而,正如插图所示,这两种断裂在本质上是相似的。(c) $P = 12\text{ MPa}$ 和 $\alpha = 24°$ 时的滑移率和 (d) 剪切应力时间历程。该实验的滑移率历史非常不同,首先传播的是亚 Rayleigh 脉冲样断裂,然后是反射超剪切裂缝样断裂。
Rupture evolution with slip
(a,b) Evolution of friction ( = shear to normal stress ratio during slip) with slip on the interface at the center of the field of view shown in Fig. 1. The four experimental ruptures have different dependence of friction on slip, indicating that the friction cannot be described by a purely slip-dependent law. (c,d) Evolution of slip rate versus slip for the same ruptures. The four ruptures are characterized by significantly different slip-rate histories, which result in different friction at any given value of slip.
(a,b) 图 1 所示视场中心界面上的摩擦力(=滑移过程中的剪应力与法向应力比)随滑移的变化。四种实验破裂的摩擦力对滑移的依赖程度不同,这表明摩擦力不能用纯粹的滑移依赖定律来描述。(c,d) 相同断裂的滑移率随滑移的变化。四条断裂的滑移率历史具有明显不同的特征,这导致在任何给定滑移值下的摩擦力都不同。
Evolution of dynamic friction with slip rate
Friction evolution is presented for the experiments at two far-field loads, $P = 7.4\text{ MPa}$ (red) and $P = 23\text{ MPa}$ (blue) and angle $\alpha = 29°$. These curves correspond to the two ruptures shown in Figs 4a,b and 5a,c. Both cases show initial strengthening with slip rate (direct effect) followed by rate weakening, as captured by rate-and-state formulations. Note that the steady-state level of dynamic friction depends on the slip rate ($f_{d} = 0.39$ for $V_{ss} = 0.87\text{ m s}^{-1}$ and $f_{d} = 0.26$ for $V_{ss} = 6.5\text{ m s}^{-1}$).
在两个远场载荷下的摩擦演化曲线分别为:$P = 7.4\text{ MPa}$ (红色)和 $P = 23\text{ MPa}$ (蓝色),角度为 $\alpha = 29°$。这些曲线对应于图 4a,b 和图 5a,c 所示的两次断裂。两种情况都显示了随着滑移速率的增加,最初的强度增强(直接效应),然后是速率减弱,速率与状态公式可以捕捉到这一点。请注意,动态摩擦的稳态水平取决于滑移率($V_{ss} = 0.87\text{ m s}^{-1}$ 时为 $f_{d} = 0.39$,$V_{ss} = 6.5\text{ m s}^{-1}$ 时为 $f_{d} = 0.26$)。
Steady propagation of spontaneously evolving ruptures
(a) Sketch of the specimen configuration showing the field of view and the locations corresponding to the slip-rate curves. (b–d) Slip-rate time histories (averaged over 1 mm) obtained at the three selected locations along the interface, for $P = 7.4\text{ MPa}$ (b) and $P = 23\text{ MPa}$ (d) respectively. (c–e) The time histories at locations L1 and L3 are time shifted (respectively, forward and backward) by $\Delta t = d/V_{r}$, where $d$ is the distance between L1 and L2 (and also L2 and L3) and $V_{r}$ is the rupture speed. The near-perfect overlap of the shifted time histories at locations L1 and L3 with the time history at L2 shows that the ruptures are well developed and propagate in a steady fashion through our field of view.
(a) 试样结构草图,显示视场和滑移率曲线对应的位置。(b-d) 分别在 $P = 7.4\text{ MPa}$ (b) 和 $P = 23\text{ MPa}$ (d) 条件下,沿界面三个选定位置获得的滑移率时间历程(1 毫米内的平均值)。(c-e) 位置 L1 和 L3 上的时间历史记录通过 $\Delta t = d/V_{r}$ 进行时间偏移(分别向前和向后),其中 $d$ 是 L1 和 L2(以及 L2 和 L3)之间的距离,$V_{r}$ 是断裂速度。L1 和 L3 位置的移动时间历史记录与 L2 位置的时间历史记录几乎完全重合,这表明断裂发展良好,并以稳定的方式在我们的视场中传播。
Steady-state friction versus slip rate
(a) Experimental measurements of steady-state friction coefficient versus slip rate and fits with the standard rate-and-state friction formulation (green curve), and combined formulation of rate-and-state friction enhanced by flash heating (black curve). Our steady-state measurements are consistent with the combined formulation. Green dots are low-velocity measurements obtained in collaboration with Kilgore, Beeler, and Lu and reported in Lu. Red, blue, black and purple solid symbols are measurements obtained with the smallest field of view used in this study ($18 \times 11.2\text{ mm}^{2}$) and hence the highest level of accuracy. The green, black and purple empty diamonds are measurements with larger fields of view (up to $145 \times 91\text{ mm}^{2}$) and lower levels of accuracy. (b) Experimental measurements of dynamic friction on quartzite samples, showing similar behaviour for rocks, with significant slip-rate dependence of friction for high steady-state slip rates, consistent with the flash heating formulation. Note the different horizontal scale for the two plots.
(a) 稳态摩擦系数与滑移速率的实验测量结果,以及与标准速率-状态摩擦公式(绿色曲线)和通过闪热增强速率-状态摩擦的组合公式(黑色曲线)的拟合结果。我们的稳态测量结果与组合公式一致。绿点是与 Kilgore、Beeler 和 Lu 合作获得的低速测量结果,并在 Lu 中进行了报道。红色、蓝色、黑色和紫色实心符号是本研究中使用的最小视场($18 \times 11.2\text{ mm}^{2}$)获得的测量结果,因此精确度最高。绿色、黑色和紫色的空菱形是使用较大视场(最多为 $145 \times 91\text{ mm}^{2}$)和较低精度水平进行的测量。


