Abstract
We study the rheology of a dense granular suspension under shear strain with the simultaneous detection of multiply scattered ultrasound through the shear band. At a low shear rate, the dissipation is rate-independent and determined by the frictional contacts between grains. Under quasistatic shear, the stress–strain curve contains elastic loading parts interrupted by stress drops. Such an intermittency is concomitant with some large decorrelation events as measured by the ultrasound probe, sensitive to the position of the grains.
Under cyclic shear, the correlations between the scattered ultrasonic waves show that at low shear strain, the grains exhibit reversible motion. Beyond this linear regime, some irreversible motion of the grains is detected. Moreover, the correlation between successive ultrasound signals suggests that some specific rearrangements, which add to the homogeneous flow, take place near the maximum strain.
我们研究了剪切应变下致密颗粒悬浮液的流变学,同时检测了通过剪切带的多重散射超声波。在低剪切速率下,耗散与速率无关,由颗粒之间的摩擦接触决定。在准静态剪切条件下,应力-应变曲线包含弹性加载部分和应力下降部分。这种间歇性与超声探头测量到的一些大的去相关事件同时发生,对颗粒的位置非常敏感。
在循环剪切下,散射超声波之间的相关性表明,在低剪切应变下,晶粒表现出可逆运动。超过这一线性范围,就会检测到晶粒的一些不可逆运动。此外,连续超声波信号之间的相关性表明,在最大应变附近会发生一些特定的重新排列,从而增加均匀流动。
Introduction
Systems that contain a large number of particles, such as foams, emulsions, colloidal suspensions or granular materials, are commonly solid at small stresses and high volume fraction, and liquid otherwise. Of particular interest is the structural signature of the transition between the two states, with the emergence of non-affine flow defects, also known as shear transformation zones, when the shear stress approaches the yield stress.
含有大量颗粒的体系,如泡沫、乳液、胶体悬浮液或颗粒材料,在应力小、体积分数高时通常呈固态,反之则呈液态。当剪切应力接近屈服应力时,会出现非线性流动缺陷,也称为剪切转化区(STZ)。
The existence of flow defects is predicted by theory, and they are indeed observed in different systems such as colloidal glasses, foams, emulsions and granular media. In granules, the analysis is often limited to fluidized systems, surface flow, slow flow or 2D geometry.
理论预测了流动缺陷的存在,而且在胶体玻璃、泡沫、乳液和颗粒介质等不同系统中也确实观察到了流动缺陷。在颗粒介质中,分析通常局限于流化系统、表面流动、慢速流动或二维几何形状。
In 3D dry granular media, acoustic waves propagate through the force-chain networks and the analysis of both longwavelength coherent waves and multiply scattered coda waves shows that anisotropy as well as contact breaking and forming are essential ingredients of the structural change under shear reversal.
Moreover, the evolution of the correlation function $\Psi$ of the multiply scattered ultrasound demonstrates a clear concomitance between the rearrangements of the force-chain network and the intermittency of the mechanical response during steady shearing. However, under low pressure the coordination number decreases and measurements are difficult due to the heterogeneity of force chains.
在三维干燥颗粒介质中,声波通过力链网络传播,对长波相干波和多重散射尾波的分析表明,各向异性以及接触断裂和形成是剪切反转下结构变化的基本要素。
此外,多散射超声波的相关函数 $\Psi$ 的演变表明,在稳定剪切过程中,力链网络的重新排列与机械响应的间歇性之间存在明显的一致性。然而,在低压条件下,配位数会减少,而且由于力链的异质性,测量会很困难。
In this respect, dense granular suspensions sheared in the quasistatic regime, as for vanishing inertial number, are attractive systems since their mechanical response will be similar to the dry case (it is also determined by the forcechain network) but the ultrasound now propagates easily through the liquid phase.
Therefore, multiply scattered ultrasound is primarily sensitive to grain (scatterer) positions, as in Diffusing Acoustic Wave Spectroscopy (DAWS). In DAWS measurements, the random motion of the particles such as the mean transport free path can be characterized by the autocorrelation function of the temporal fluctuations of scattered sound waves, via configurational averaging and in the diffusion approximation.
Here, we probe reversibility and intermittency in a dense granular suspension under cyclic and steady shear at a low shear rate and under low pressure. Unlike DAWS measurements in fluidized suspensions of particles with possible configurational averaging, we will only use the autocorrelation function of the multiply scattered ultrasound $\Psi$ as a qualitative estimate for the overall change of grain position in such densely packed suspensions.
在这方面,在准静态条件下剪切的致密颗粒悬浮液(如惯性数消失时)是很有吸引力的系统,因为它们的机械响应与干燥情况类似(也由力链网络决定),但超声波现在很容易在液相中传播。
因此,多重散射超声波主要对颗粒(散射体)位置敏感,如扩散声波光谱法(DAWS)。在 DAWS 测量中,颗粒的随机运动(如平均传输自由路径)可通过构型平均和扩散近似散射声波时间波动的自相关函数来表征。
在此,我们将探究在低剪切速率和低压条件下,高密度颗粒悬浮液在循环和稳定剪切作用下的可逆性和间歇性。与在可能存在构型平均的颗粒流化悬浮液中进行的 DAWS 测量不同,我们将仅使用多散射超声波的自相关函数 $\Psi$ 作为对此类致密悬浮液中颗粒位置整体变化的定性估计。
Cyclic shear causes a transition from caged to irreversible grain motion at the onset of yielding. Moreover, the analysis of the nonlinear mechanical response during cyclic shearing reveals specific dynamics which may be attributed to the compaction and to the buckling of force chains.
For steady shear, the intermittency of the measured torque is concomitant with large decorrelation events. The magnitudes of the observed stress drops are weakly but significantly connected to the extent of decorrelation.
循环剪切会在屈服开始时导致晶粒运动从笼式运动过渡到不可逆运动。此外,循环剪切过程中的非线性机械响应分析揭示了特定的动态,这些动态可归因于力链的压实和屈曲。
对于稳定剪切,测量扭矩的间歇性与大的去相关事件同时发生。观察到的应力下降幅度与去相关性的程度有微弱但重要的联系。
Experiments
The granular suspension consists of spherical glass beads of diameter $d = 0.8$ or $3\text{mm}$ dispersed in water (identical results were obtained with angular sand grains). The beads are first poured into the measurement cell and the water is added slowly, resulting in an initial volume fraction $\phi\approx 0.56$. A PMMA lid sealed with grease limits evaporation. Rheological measurements are achieved in a vane-in-cup geometry (Fig. 1) by shearing the suspension at the imposed velocity with a rotating four blade vane attached to a rheometer (Wille Geotechnik), and measuring the torque $C$.
The radius of the vane $R_{0} = 1 \text{cm}$, its height $H_{0} = 3\text{cm}$, and it is inserted at a depth $h$ below the upper surface of the suspension (see Fig. 1(a)). Some fixed blades of width $1.5\text{cm}$ are stuck on the walls of the cell as shown in Fig. 1(b), resulting in a gap $\Delta R = 1.5\text{cm}$. In steady shear, the gap is sheared homogeneously in the case of the large $3\text{mm}$ beads, while localised flow is expected for the smaller beads of diameter $0.8\text{mm}$, in a shear band of width $5d$.
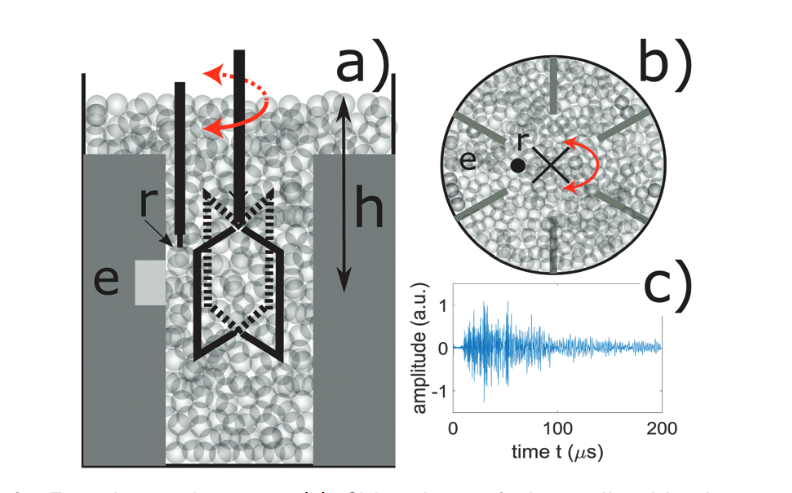
Experimental setup. (a) Side view of the cell with the vane. The emission (e) and the reception (r) of the ultrasound waves are shown. (b) Top view of the cell. The suspension is sheared between the vane and the fixed stoppers (dark grey). e: source transducer (emission) and r: receiver. (c) Typical scattered ultrasonic signal.
实验装置。(a) 带有叶片的颗粒池侧视图。图中显示了超声波的发射(e)和接收(r)。(b) 实验室俯视图。悬浮液在叶片和固定塞(深灰色)之间被剪切。(c) 典型的散射超声波信号。
颗粒悬浮液由分散在水中的直径为 $d = 0.8$ 或 $3\text{mm}$ 的球形玻璃珠组成(与角形沙粒获得的结果相同)。首先将玻璃珠倒入测量池,然后缓慢加水,初始体积分数为 $0.56$。用油脂密封的 PMMA 盖子可限制蒸发。流变学测量是在杯中叶片的几何形状中进行的(图 1),方法是用连接到流变仪(Wille Geotechnik)上的旋转四叶叶片以施加的速度剪切悬浮液,并测量扭矩 $C$。
叶片半径 $R_{0} = 1 \text{cm}$,高度 $H_{0} = 3 \text{cm}$,插入悬浮液上表面下方深度 $h$(见图 1(a))。如图 1(b) 所示,一些宽度为 $1.5\text{cm}$ 的固定叶片贴在电池壁上,从而产生了 $\Delta R = 1.5\text{cm}$ 的间隙。在稳定剪切状态下,大颗粒($3\text{mm}$)的间隙会被均匀剪切,而直径较小($0.8\text{mm}$)的颗粒则会在宽度为 $5d$ 的剪切带中发生局部流动。
Steady shear is analyzed after rotating the vane at least one full revolution at the maximum angular velocity used in this work, $\dot{\theta}=8.7\text{ mrad s}^{-1}$. The corresponding order of magnitude of the viscous number $J = \eta_{\text{f}}\dot{\gamma}/P$
$10^{-3}\times 10^{-2}/100$$10^{-7}$ as a maximum (where $\dot{\gamma} = \dot{\theta}R_{0}/\Delta R$ is the strain rate and $\eta_{\text{f}}$ is the viscosity of the liquid), ensuring quasistatic shear.The coefficient of friction of the granules can be determined by measuring $C$ for different depths $h$ at the angular velocity $\dot{\theta} = 1\text{ mrad s}^{-1}$. The shear stress $\sigma = C/2\pi R_{0}^{2}H_{0}$ is plotted in Fig. 2 against pressure $P = \phi \Delta\rho gh$ with $1.5\leq h\leq 5\text{cm}$($\Delta\rho = \rho_{g} - \rho_{w} = 2600-1000 = 1600\text{kg m}^{-3}$ is the difference in density between the glass beads and the water, and $g$ is the acceleration due to gravity).
以本研究中使用的最大角速度($\dot{\theta}=8.7\text{ mrad s}^{-1}$)旋转叶片至少一整圈后,对稳定剪切进行分析。相应数量级的粘性数 $J = \eta_{\text{f}}\dot{\gamma}/P$$10^{-3}\times 10^{-2}/100$$10^{-7}$ 为最大值(其中 $\dot{\gamma} = \dot{\theta}R_{0}/\Delta R$ 为应变率,$\eta_{\text{f}}$ 为液体的粘性), 确保准静态剪切。
在角速度 $\dot{\theta} = 1\text{ mrad s}^{-1}$下,通过测量不同深度 $h$ 的 $C$ 可以确定颗粒的摩擦系数。剪应力 $\sigma = C/2\pi R_{0}^{2}H_{0}$ 与压力 $P = \phi \Delta\rho gh$ 的关系图见图 2,其中 $1.5\leq h\leq 5\text{cm}$ ($\Delta\rho = \rho_{g} - \rho_{w} = 2600-1000 = 1600\text{kg m}^{-3}$ 是玻璃珠和水的密度差,$g$是重力加速度)。
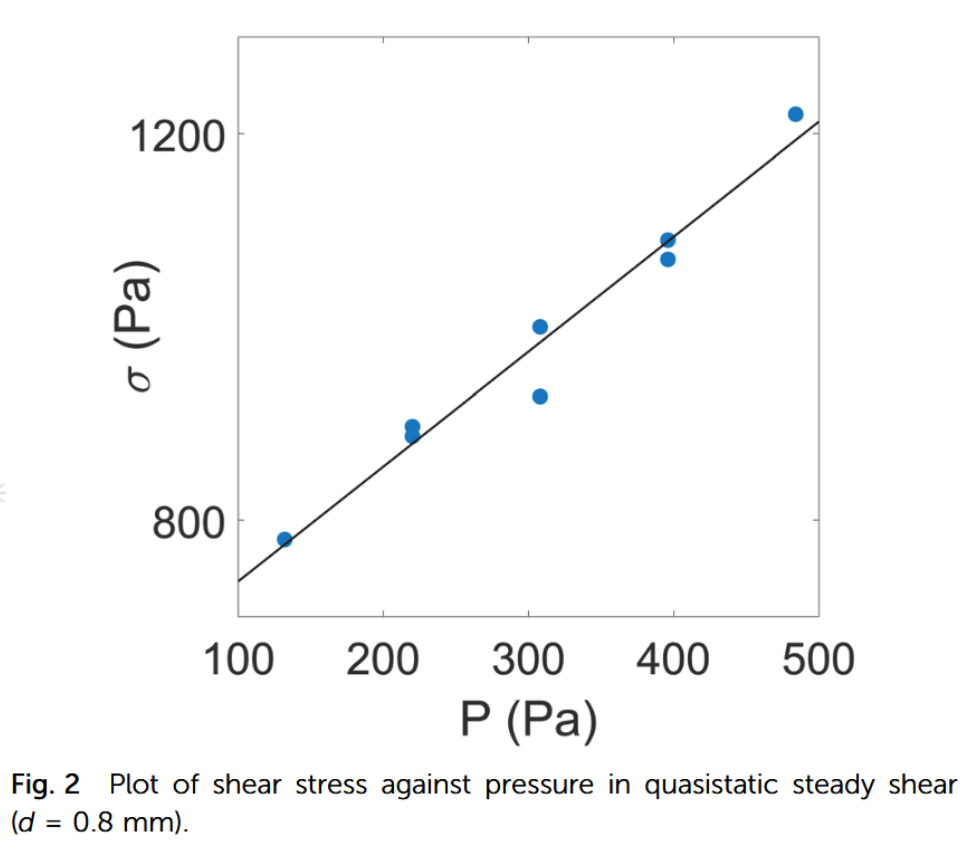
Plot of shear stress against pressure in quasistatic steady shear ($d = 0.8\text{ mm}$).
准静态稳定剪切($d = 0.8\text{ mm}$)中剪应力与压力的关系图。
The plot is affine as expected, and with $\sigma$~$\mu_{\text{d}}P$, the effective dynamic friction coefficient of the granular system obtained, $\mu_{\text{d}}=1.2$, is consistent with the results obtained by others at vanishing shear rate. At a given pressure, this value is constant within the range of angular velocities used in this study, $\dot{\theta}=5.8\times 10^{-2}$ to $8.7\text{ mrad s}^{-1}$, confirming that the system is sheared in the quasistatic regime.
正如所料,该曲线图是仿射的,在 $\sigma$~$\mu_{\text{d}}P$ 的情况下,得到的颗粒系统的有效动摩擦系数为 $\mu_{\text{d}}=1.2$,与其他人在剪切速率消失时得到的结果一致。在给定压力下,该值在本研究使用的角速度范围内($\dot{\theta}=5.8\times 10^{-2}$ 至 $8.7\text{ mrad s}^{-1}$)是恒定的,这证实了系统是在准静态机制下剪切的。
For oscillatory testing, the suspension is sheared at controlled strain rate by applying “$n$” triangular oscillations of amplitude $\pm\theta_{m}$ (see below). Shearing is always applied first at $\theta_{m}=32$° and then $\theta_{m}$ is decreased progressively down to $0.025$°. The initial largest amplitude, far beyond the yield strain, ensures a reproducible initial state with a presumably loose packing and a well-defined shear band in the gap. For the subsequent smaller amplitudes, the measured torque $C$ first evolves in time because of both the compaction effect due to the applied oscillatory strain and the motions along the flow field.
Then, the torque stabilizes after a typical number of cycles $n > 10$ (denser packing). We show this in Fig. 3(a), for which the system with $d = 0.8 \text{mm}$ was first prepared with $n = 8$ cycles at $\theta_{m}=32$° and then directly brought to $\theta_{m}=0.025$°. The measured torque, separated arbitrarily in groups of $10$ cycles $(1–6)$, increases and reaches a well-defined amplitude and mean value after approximately $50$ cycles (group $6$).
In this paper, we discuss only those cycles for which the system has reached a given compaction state where the torque has a constant mean over $n \gg 510$ cycles. Compaction is therefore assumed to play a negligible role in the time evolution of the oscillatory mechanical response and the associated ultrasonic signals. After stabilization, the averaged torque is subtracted from the instantaneous value.
在振荡测试中,通过施加振幅为 $\pm\theta_{m}$ 的 “$n$” 三角振荡(见下文),以受控应变率对悬浮液进行剪切。剪切总是首先在 $\theta_{m}=32$° 时进行,然后将 $\theta_{m}$ 逐步降至 $0.025$°。最初的最大振幅远远超过了屈服应变,确保了可重现的初始状态,即在间隙中形成假定的松散堆积和清晰的剪切带。对于随后的较小振幅,由于外加振荡应变产生的压实效应和沿流场的运动,测得的扭矩 $C$ 首先随时间发生变化。
然后,在典型的循环次数 $n > 10$(更密集的堆积)之后,扭矩趋于稳定。我们在图 3(a) 中展示了这一点,在该图中,$d = 0.8 \text{mm}$ 的系统首先在 $\theta_{m}=32$° 下进行了 $n = 8$ 次循环,然后直接进入 $\theta_{m}=0.025$°。测量到的扭矩以 $10$ 周期 $(1-6)$为一组任意分开,在大约 $50$ 周期(第 $6$ 组)后增加并达到明确的振幅和平均值。
在本文中,我们只讨论系统已达到给定压实状态的循环,在这种状态下,扭矩在 $n \gg 510$ 循环中具有恒定的平均值。因此,我们假定压实在振荡机械响应和相关超声波信号的时间演化过程中的作用可以忽略不计。稳定后,从瞬时值中减去平均扭矩。
Ultrasonic measurements are achieved with a large immersion source transducer of diameter $2.4 \text{cm}$ excited at $2.5 \text{MHz}$, whose center is placed at a depth $h$ and inserted between the fixed blades (see Fig. 1). The wavelength $\lambda$~$600\mu\text{m}$ is close to the diameter of the particles. Multiply scattered waves are detected with a small transducer of diameter $2 \text{mm}$ ("$r$" in Fig. 1), placed in the sheared volume with the tip located at $h$. For the purpose of monitoring structural changes during the shearing of the granular suspension, we determine the zero time lag cross correlation $A_{i,j}$ between two signals $S_{i}(t)$ and $S_{j}(t)$.
Then, the normalized correlation function $\Psi_{i,j} = A_{i,j}/(A_{i,i}A_{j,j})^{1/2}$ gives a measure of the resemblance between two ultrasonic speckles and measures qualitatively the difference in the spatial arrangement of the grains:$\Psi_{i,j} = 1$ means a perfect similarity between two packing structures while $\Psi_{i,j} < 1$ reveals positional changes of the grains. The lower bound for the typical grain displacement detected by the decorrelation between speckles is $\lambda/4$~$150\mu\text{m}$.
超声波测量是通过一个直径为 $2.4 \text{cm}$、激励频率为 $2.5 \text{MHz}$的大型浸入源传感器实现的,该传感器的中心位于深度 $h$,并插入固定叶片之间(见图 1)。波长 $\lambda$~$600\mu\text{m}$ 与粒子直径接近。多重散射波通过一个直径为 $2\text{mm}$(图 1 中的"$r$")的小型传感器检测,该传感器放置在剪切体积中,尖端位于 $h$。为了监测颗粒悬浮液剪切过程中的结构变化,我们确定了两个信号 $S_{i}(t)$ 和 $S_{j}(t)$ 之间的零时滞交叉相关性 $A_{i,j}$。
然后,归一化相关函数 $\Psi_{i,j} = A_{i,j}/(A_{i,i}A_{j,j})^{1/2}$ 可以测量两个超声波斑点之间的相似度,并定性地测量晶粒空间排列的差异:$\Psi_{i,j} = 1$ 表示两个堆积结构完全相似,而 $\Psi_{i,j}< 1$ 则表明晶粒的位置发生了变化。通过斑点间的去相关性检测到的典型颗粒位移的下限是 $\lambda/4$~$150\mu\text{m}$。
As an example of ultrasonic measurement, Fig. $3(b)$ shows the evolution of the decorrelation of ultrasonic signals $\Psi_{1,i}$ during cyclic shear at $\theta_{m}=0.025$°. Here, the reference signal ‘$1$’ corresponds to the first point of each group of $10$ cycles as discussed above.
There is a progressive decorrelation of ultrasonic signals with increasing number of cycles, which reflects irreversible grain motions due to both compaction and grain motion along the flow field. However, the evolution of $\Psi_{1,i}$ for the successive series $(1)$ to $(6)$ suggests that the compacted system reaches a state close to reversibility after a sufficient number of cycles of shearing.
作为超声波测量的一个示例,图 $3(b)$ 显示了在 $\theta_{m}=0.025$° 循环剪切过程中超声波信号 $\Psi_{1,i}$ 的去相关性的演变。在这里,参考信号 “$1$” 对应于上文讨论的每组 $10$ 周期的第一个点。
随着循环次数的增加,超声波信号的相关性逐渐减弱,这反映了由于压实和晶粒沿流场运动而产生的不可逆晶粒运动。然而,$(1)$ 至 $(6)$ 连续序列的 $\Psi_{1,i}$ 的演变表明,在经过足够次数的剪切循环后,压实系统达到了接近可逆的状态。
Results and discussion
Steady shear and intermittency
We now analyze the dynamics of the liquid state in steady shear with a system of large particles with $d = 3\text{mm}$ sheared at $\dot{\theta} = 5.8\times 10^{-2}\text{mrad s}^{-1}$. The measured torque is plotted in Fig. 4(a). The intermittent nature of the stress, characterized by portions of elastic mechanical loading and sudden stress drops $\Delta\sigma$,is well-documented for driven amorphous systems. For each elastic branch, the elastic strain is $\Delta\gamma_{\text{el}} = \Delta\theta_{\text{el}}R_{0}/\Delta R$, and since $\Delta\sigma_{\text{el}} = G\Delta\gamma_{\text{el}}$, fitting the elastic loadings provides a shear modulus $G\text{~}4\pm 1\times 10^{5}\text{Pa}$.
现在我们来分析稳定剪切状态下的液态动力学,大颗粒系统的剪切速度为 $\dot{\theta} = 5.8\times 10^{-2}\text{mrad s}^{-1}$,剪切力为 $d = 3\text{mm}$ 。测得的扭矩如图 $4(a)$ 所示。应力的间歇性特点是部分弹性机械负载和应力骤降,这在非晶体驱动系统中得到了充分证明。对于每个弹性分支,弹性应变为 $\Delta\gamma_{\text{el}} = \Delta\theta_{\text{el}}R_{0}/\Delta R$,由于 $\Delta\sigma_{\text{el}} = G\Delta\gamma_{\text{el}}$ ,拟合弹性载荷可得到剪切模量 $G\text{~}4\pm 1\times 10^{5}\text{Pa}$.
Then, from the independent order of magnitude of the stress drops $\Delta\sigma$
$10^{2}-10^{4}\text{Pa}$ and with $\Delta\sigma$$G\Delta\gamma_{\text{pl}}$ ($\gamma_{\text{pl}}$ is the plastic strain), an estimate for the size a of plastic events can be obtained from $\Delta\gamma_{\text{pl}}$$a/\Delta R$, $a$$4–400\mu\text{m}$ within the range of the resolution $\lambda/4$. Since these plastic rearrangements are concomitant with stress drops, they will involve force chains. Such dynamics therefore occur on a timescale $t_{\text{chain}}$$l/v_{s}$ where $l$$\Delta R$ is the length of the force chains and $v_{s}$$(G/\rho)^{1/2}$$15\text{m s}^{-1}$ is the velocity of sound in the dry packing. This gives $t_{\text{chain}}$~$1\text{ms}$ at most, much faster than the acquisition time of the ultrasound signals $t_{\text{acq}} = 1 \text{s}$: events appear to be instantaneous.
然后,从应力下降的独立数量级 $\Delta\sigma$$10^{2}-10^{4}\text{Pa}$ 和 $\Delta\sigma$$G\Delta\gamma_{\text{pl}}$($\gamma_{\text{pl}}$ 是塑性应变)可以得到塑性事件大小a的估计值、从 $\Delta\gamma_{\text{pl}}$$a/\Delta R$, $a$$4-400\mu\text{m}$ 在分辨率 $\lambda/4$ 的范围内,可以得到塑性事件大小 a 的估计值。由于这些塑性重排与应力下降同时发生,它们将涉及力链。因此,这种动力学发生的时间尺度为 $t_{\text{chain}}$$l/v_{s}$,其中 $l$$\Delta R$ 是力链的长度,$v_{s}$$(G/\rho)^{1/2}$$15\text{m s}^{-1}$ 是干燥堆积中的声速。由此得出 $t_{\text{chain}}$~$1\text{ms}$ 最多比超声波信号的采集时间 $t_{\text{acq}} = 1 \text{s}$ 快得多:事件似乎是瞬时发生的。
These instantaneous stress drops are clearly concomitant with bursts of $\Psi_{i,i+1}$ (of amplitude $\Psi^{\star}$), as shown in Fig. 4(a). This signature is identical to the one obtained in previous work, although these ultrasonic waves propagate through the saturating liquid rather than through the contact network.
如图 4(a)所示,这些瞬时应力下降明显与 $\Psi_{i,i+1}$(振幅为 $\Psi^{\star}$)的爆发同时发生。尽管这些超声波是通过饱和液体而不是接触网络传播的,但这一特征与之前工作中获得的特征相同。
Beyond a cutoff $\Psi^{\star} > 0.1$, the amount of decorrelation, corresponding to the extent of local positional rearrangements of the grains, seems to be correlated to the intensity of stress drops as shown in Fig. 4(b).
This is likely due to the fact that larger stress drops correspond to large positional rearrangements of grains which are well detected by the ultrasound speckles correlation $\Psi^{\star}$. At low decorrelation however, the correspondence is lost as shown by the plateau at $\Psi^{\star} < 0.1$.
Here, the stress drop can be related to different amounts of local rearrangements in the case of slipping without significant change of grain positions or rearrangement of grains that are not involved in force chains. While this may be due to the heterogeneity of the force chains at such low pressure, the lack of theoretical description for $\Psi$ limits further analysis.
在临界值 $\Psi^{\star}>0.1$ 时,与晶粒局部位置重排程度相对应的去相关性的大小似乎与应力下降的强度相关,如图 $4(b)$ 所示。
这可能是由于较大的应力下降对应于较大的晶粒位置重排,而超声斑点相关性 $Psi^{\star}$ 可以很好地检测到这一点。然而,在较低的去相关性下,这种对应关系就会消失,如 $\Psi^{\star}< 0.1$ 时的平面所示。
在这里,应力下降可能与滑动情况下不同数量的局部重排有关,而晶粒位置或未参与力链的晶粒重排没有显著变化。虽然这可能是由于在如此低的压力下力链的异质性造成的,但缺乏对 $\Psi$ 的理论描述限制了进一步的分析。
Cyclic shear
Effective modulus and hysteresis cycles
For a system of small particles of diameter $0.8\text{mm}$, some representative hysteresis loops are reported in Fig. 5(a), where we plot the measured torque $C$ as a function of the applied rotation angle. For the smallest shear strain corresponding to $\theta_{m} = 0.025-0.05$°, the suspension is elastic and the response is essentially linear (see Fig. 6(a), $\theta_{m}=0.025$° for an enlarged view). With the geometry used, the applied strain in the linear regime $\gamma = \theta_{m}R_{0}/\Delta R$ and at the lowest amplitudes the typical shear modulus $G(0.025°)=\sigma/\gamma$
$6\times 10^{5}$ and $G(0.05°)$$5\times 10^{5}\text{Pa}$ as found by others.
对于直径为 $0.8\text{mm}$ 的小颗粒系统,一些具有代表性的滞后环见图 5(a),图中我们绘制了测量扭矩 $C$ 与所施加旋转角度的函数关系。在最小剪切应变 $\theta_{m}=0.025-0.05$° 时,悬架是弹性的,响应基本上是线性的(放大图见图 6(a),$\theta_{m}=0.025$°)。根据所使用的几何形状,线性状态下的应用应变为 $\gamma = \theta_{m}R_{0}/\Delta R$,在最低振幅下,典型的剪切模量为 $G(0.025°)=\sigma/\gamma$$6\times 10^{5}$ 和 $G(0.05°)$$5\times 10^{5}\text{Pa}$ (如其他人所发现的)。
Larger rotation angles $0.25° < \theta_{m} < 8°$ give rise to non-linear behavior, with the specific distorted hysteresis loops. In this elastoplastic regime, the hysteresis loops exhibit strain stiffening close to $\pm\theta_{m}$, probably linked to the development of an anisotropic structure via the force chains. The intra-cycle strain stiffening is, however, accompanied by a global softening with a decrease in the effective mean secant stiffness $C_{m}/\theta_{m}$ as shown in Fig.5(c).
更大的旋转角度 $0.25° < \theta_{m}< 8°$ 会产生非线性行为,具体表现为滞后环扭曲。在这种弹塑性机制下,滞后环表现出接近 $\pm\theta_{m}$ 的应变硬化,这可能与通过力链形成各向异性结构有关。然而,如图 5(c)所示,周期内的应变硬化伴随着全局软化,有效平均正弦刚度 $C_{m}/\theta_{m}$ 下降。
Well above failure, for $\theta_{m} = 16-32°$, Fig. 5(a) shows an established granular flow with large hysteresis, corresponding to the liquid state (see also Fig. 5(b) and (c)). The area of the cycles $A = \int C(\theta)\mathrm{d}\theta$, which is independent of the shear rate in the range explored (not shown), is compared in Fig. 5(b) with that given by idealized hysteresis loops described by the Coulomb frictional (rectangular) cycle such that $A_{c}$~$8\pi\mu_{c}PR_{0}^{2}H_{0}\theta_{m}$. Plotting $A/\theta_{m}$ from experiments gives a constant value at large rotation angle as shown in Fig. 5(b) (dotted line), providing $\mu_{c}\approx 0.6$, similar to that obtained above for steady shear.
From the analysis of multiply scattered ultrasound, we shall now investigate the signature of the transition to the non-linear regime, as well as some specific dynamics of grain rearrangements under cyclic shear.
图 $5(a)$ 显示了与液态相对应的具有大滞后性的颗粒流动(另见图 $5(b)$ 和 $(c)$)。在图 $5(b)$ 中,循环的面积 $A = \int C(\theta)\mathrm{d}\theta$ 与所探讨范围内的剪切速率无关(未显示),它与库仑摩擦(矩形)循环描述的理想化滞后环给出的面积进行了比较,库仑摩擦(矩形)循环的面积为 $A_{c}$~$8\pi\mu_{c}PR_{0}^{2}H_{0}\theta_{m}$。将实验得出的 $A/\theta_{m}$ 绘制成图,如图 $5(b)$ (虚线)所示,在大旋转角度下会得到一个恒定值,提供了 $\mu_{c}\approx 0.6$,这与上文针对稳定剪切力得到的值类似。
通过对多散射超声波的分析,我们现在将研究向非线性机制转变的特征,以及在循环剪切作用下晶粒重排的一些具体动态。
Reversibility probed by multiply scattered waves
Fig. 6(a) shows, for various angles $\theta_{m}$, the simultaneous measurements of the torque and of $\Psi_{1,j}$. Here, the subscript $1$ refers to the initial configuration at $t = 0$, with $\theta = -\theta_{m}$. For the lowest amplitudes in the linear regime (see $\theta_{m} = 0.025°$ in Fig. 6(a)), $\Psi_{1,j}$ decreases slightly upon applying shear during the first half-cycle, and recovers its initial value of ~$1$ upon shear reversal.
Hence, some grains are slightly displaced by the applied shear and come back to close to their original position at the end of the cycle. Grain motion is reversible, reminiscent of caged motion.
In the range $0.05° < \theta_{m} \leq 0.25°$, there is a specific amplitude above which the correlation function $\Psi_{1,j}$ does not return to the value recorded during the preceding cycle. As shown in Fig. 6(a) for $\theta_{m} = 0.25°\rightarrow 4°$, this corresponds to a constant remnant decorrelation when $\theta$ returns to $-\theta_{m}$. We quantify this effect by defining the “strobed” $\Delta\Psi$ as the average variation of the decorrelation over a period, as illustrated in Fig. 6(b) and plotted in the inset as a function of $\theta_{m}$.
图 6(a) 显示了不同角度 $\theta_{m}$ 时扭矩和 $\Psi_{1,j}$ 的同步测量结果。这里,下标 $1$ 指的是 $t = 0$ 时的初始配置,即 $\theta = -\theta_{m}$。对于线性机制中的最低振幅(见图 $6(a)$ 中的 $\theta_{m} = 0.025°$),在第一个半周期中施加剪切力时,$\Psi_{1,j}$ 会略微减小,而在剪切力反转时会恢复其初始值 ~$1$。
因此,一些颗粒会因施加的剪切力而发生轻微位移,并在循环结束时回到接近其原始位置的位置。颗粒运动是可逆的,让人联想到笼式运动。
在 $0.05° < \theta_{m}\leq 0.25°$ 的范围内,存在一个特定的振幅,超过这个振幅,相关函数 $\Psi_{1,j}$ 就不会恢复到前一个周期记录的值。如图 $6(a)$ 中 $\theta_{m} = 0.25°\rightarrow 4°$ 所示,当 $\theta$ 返回到 $-\theta_{m}$ 时,这相当于一个恒定的残余去相关性。我们将 “频闪” $\Delta\Psi$ 定义为一个周期内去相关性的平均变化来量化这种效应,如图 $6(b)$ 所示,并在插图中绘制为 $\theta_{m}$ 的函数。
While this signature could correspond to a homogeneous deformation of the whole granular media, we believe that it is rather reminiscent of local motions of a small number of grains and could indicate that while a fraction of the grains in the sheared zone show reversible displacement during a given cycle, other grains do not return to their original position. More work is needed to quantitatively link $\Delta\Psi$ to structural rearrangements, yet the finite $\Delta\Psi$ suggests that a constant fraction of the grains are displaced irreversibly, and that those grains correspond to a population that is renewed during each cycle.
虽然这种特征可能与整个颗粒介质的均匀变形相对应,但我们认为它更像是少数晶粒的局部运动,并可能表明,虽然剪切区中的一部分晶粒在给定周期内表现出可逆位移,但其他晶粒并没有回到它们原来的位置。我们还需要做更多的工作来定量地将 $\Delta\Psi$ 与结构重排联系起来,然而有限的 $\Delta\Psi$ 表明,恒定的一部分晶粒发生了不可逆的位移,这些晶粒对应于在每个周期中更新的群体。
Importantly, the amplitude $0.05° < \theta_{m} \leq 0.25°$, at which a transition from zero to finite decorrelation is observed, matches closely the rheological transition from the linear elastic regime to the non-linear elastoplastic one as shown in Fig. 5(c).
For the largest amplitudes $\theta_{m} > 8°$, $\Delta\Psi$ approaches 1 quickly, suggesting that above failure, the proportion of grains returning to their original positions after a cycle vanishes.
重要的是,在振幅 $0.05° < \theta_{m} \leq 0.25°$处,可以观察到从零到有限不相关的过渡。,此时观察到从零到有限去相关性的过渡,如图 5(c)所示,这与从线性弹性体系到非线性弹塑性体系的流变学过渡非常吻合。对于最大振幅 $\theta_{m}>8°$ 时,$\Delta\Psi$ 很快接近 $1$, 这表明在失效以上,一个周期后返回原位的晶粒比例消失了。
The above results provide insights into some basic mechanics at work during the transition from the elastic to the plastic state, i.e., grain motion becomes irreversible. The non-linear regime is clearly dominated by the friction arising from contacts between grains, but the analysis of the correlation between successive speckles for large $\theta_{m}$ provides evidence for a specific type of dissipative event, discussed in the following section.
上述结果提供了从弹性状态过渡到塑性状态(即晶粒运动变得不可逆)期间一些基本力学工作的见解。非线性机制显然是由晶粒间接触产生的摩擦力主导的,但对大 $\theta_{m}$ 时连续斑点间相关性的分析为下一节讨论的特定类型耗散事件提供了证据。
Dynamics of shear reversal
For example, the correlation function $\Psi_{i,i+1}$ probes the system at a time interval $t_{\text{acq}} =1\text{s}$, corresponding to the time lapse between two successive acquisitions of acoustic ultrasonic signals. In Fig. 7, the system is sheared at a shear rate $\dot{\gamma}(\text{max})$
$R_{0}\dot{\theta}(\text{max})/\Delta R$$10^{-2}\text{s}^{-1}$ where we have taken the width of the gap $\Delta R$$5d$ and $\dot{\theta}(\text{max}) = 8.7\text{ mrad s}^{-1}$. This provides a characteristic timescale $t_{\text{shear}} = 1/\dot{\gamma}(\text{max})$$100\text{s}$ for a putative homogeneous flow. With $t_{\text{acq}} \ll t_{\text{shear}}$, grains barely flow during the time lapse between the two signals and this results in small detected positional rearrangements on average with $\Psi_{i,i+1}\approx 1$.However, inspection of the evolution of $\Psi_{i,i+1}$ within individual cycles in Fig. 7 reveals that when shear reversal has just occurred, successive scattered ultrasonic waves are more correlated than when approaching $\theta_{m}$ with strain stiffening.
例如,相关函数 $\Psi_{i,i+1}$ 在时间间隔 $t_{text{acq}} =1\text{s}$,即两次连续采集超声波信号之间的时间间隔内探测系统。在图 7 中,系统以剪切率 $\dot{\gamma}(\text{max})$$R_{0}\dot{\theta}(\text{max})/\Delta R$$10^{-2}\text{s}^{-1}$ 进行剪切,其中我们取间隙宽度 $\Delta R$$5d$ 和 $\dot{\theta}(\text{max}) = 8。7text{ mrad s}^{-1}$。这为推定的均质流提供了一个特征时间尺度 $t_{text{shear}} = 1/\dot{gamma}(\text{max})$$100\text{s}$ 。有了 $t_{\text{acq}} \ll t_{\text{shear}}$ 时,颗粒在两个信号之间的时间间隔内几乎不流动,这导致检测到的位置重排很小,平均为 $\Psi_{i,i+1}\approx 1$。
然而,通过观察图 7 中各个周期内 $\Psi_{i,i+1}$ 的变化可以发现,当剪切反转刚刚发生时,连续的散射超声波比接近应变硬化的 $\theta_{m}$ 时更加相关。
This points to specific positional rearrangement dynamics when approaching $\theta_{m}$, which occur at a higher rate than that provided by the average flow at low $\dot{\gamma}$. For $\theta$ just below $\theta_{m}$, as shown in Fig. 8(a), the shear builds up the oriented anisotropic strong force chains along the compressional direction. They may buckle, disappear and reform under the sustained shear if the threshold is locally exceeded via slips, causing significant positional rearrangements of grains (Fig. 8(a)).
这表明在接近 $\theta_{m}$ 时存在特定的位置重排动力学,其速率高于低 $\dot{\gamma}$ 时的平均流速。对于刚刚低于 $\theta_{m}$ 的 $\theta$,如图 8(a)所示,剪切力会沿着压缩方向形成定向各向异性的强力链。如果通过滑移局部超过阈值,它们可能会在持续剪切力作用下发生弯曲、消失和重组,从而导致晶粒位置的显著重排(图 8(a))。
After shear reversal, however, the force chains vanish and a more homogeneous slow flow is expected. Taking into account the vanishing shear rate, few rearrangements if any occur after reversal (Fig. 8(b)). Hence we believe that the dynamics detected by multiply scattered ultrasound, sensitive to the positional changes of grains and transiting through the liquid phase, may provide an indirect measure of the buildup of force chains due to the applied shear.
然而,剪切反转后,力链消失,预计会出现更均匀的缓慢流动。考虑到剪切速率的消失,反转后即使有重新排列也很少发生(图 8(b))。因此,我们认为多散射超声波检测到的动态对晶粒的位置变化和通过液相的过程非常敏感,可以间接测量外加剪切力导致的力链的形成。
Conclusion
In the liquid state under steady shear we observed concomitant intermittency between the local ultrasonic speckle probe and the macroscopic measured stress, associated with significant fast rearrangements of particle positions.
For cyclic shear, the correspondence between the correlation function of ultrasonic speckles and the measured mechanical properties implies that the elastic, weakly hysteretic solid corresponds to well-correlated signals and recoverable structure at low amplitudes.
The transition to the elastoplastic state is identified as arising from irreversible motion of a small fraction of grains, detected by the periodic persistent decorrelation. At higher amplitudes, thanks to the analysis of the correlation function between successive speckles, some specific rearrangements are detected, ascribed to the dynamics of force chains.
在稳定剪切下的液态中,我们观察到局部超声波斑点探头与宏观测量应力之间的间歇性,这与颗粒位置的显著快速重排有关。
对于循环剪切,超声波斑点的相关函数与测得的机械特性之间的对应关系意味着,弹性、弱滞后固体对应于相关性良好的信号和低振幅下的可恢复结构。
向弹塑性状态的转变是由一小部分晶粒的不可逆运动引起的,通过周期性持续的去相关性可以检测到。在振幅较高的情况下,通过分析连续斑点之间的相关函数,可以检测到一些特定的重新排列,这归因于力链的动态变化。
Under oscillatory shear strain, irreversible rearrangements of the particles in suspensions can arise from several mechanisms, from “simple” binary (frictional) contacts to cooperative motion in shear transformation zones. Recently, a series of studies showed that in fact, the onset of irreversibility depends on a strain amplitude threshold $\gamma = \gamma(\phi)$ beyond which particle trajectories are chaotic.
In the present work, reversibility is only probed at small strain amplitudes and with a limited number of oscillations. We believe that our results provide a convenient framework for studying whether limit cycles or memory effects can be observed experimentally in such nonlinear, frictional and dense systems.
在振荡剪切应变作用下,悬浮液中颗粒的不可逆重排可能来自多种机制,从 “简单的” 二元(摩擦)接触到剪切转换区的合作运动。最近,一系列研究表明,事实上,不可逆的开始取决于应变振幅阈值 $\gamma = \gamma(\phi)$, 超过这个阈值,粒子轨迹就会混乱。
在本研究中,只在应变振幅较小和振荡次数有限的情况下探测可逆性。我们相信,我们的研究结果为研究在此类非线性、摩擦和致密系统中是否能通过实验观察到极限循环或记忆效应提供了一个方便的框架。

