DOI: 10.1029/2008GL035264
Abstract
Nonlinear sound propagation in a stressed glass bead pack is investigated via amplitude measurements of harmonic generation. We evidence two distinct regimes of sound-matter interaction: reversible and irreversible, as a function of the ratio $r_{s}$ between dynamic strain and static one.
In the reversible regime, the higher harmonics generated agree well with a mean-field model based on the Hertz contact theory, and the coefficient of nonlinearity $\beta$ deduced from the measured amplitude of second-harmonic is consistent with that deduced from the acoustoelastic measurement.
Beyond a certain threshold ($r_{s} > 3\text{%}$), the interaction of sound wave with granular matter becomes irreversible, accompanied by a small compaction of the medium.
我们通过测量谐波激发的振幅,研究了声音在受压玻璃球堆积中的非线性传播。根据动态应变与静态应变之比 $r_{s}$ 的函数关系,我们证明了声物质相互作用的两种截然不同的状态:可逆和不可逆。
在可逆机制下,激发的高次谐波与基于 Hertz 接触理论的平均场模型非常吻合,从测量的二次谐波振幅推导出的非线性系数 $\beta$ 与声弹性测量推导出的非线性系数一致。
超过一定阈值($r_{s} > 3\text{%}$)后,声波与颗粒物质的相互作用变得不可逆,并伴随着介质的微小压实。
Introduction
In a dense granular packing (solid volume fraction $\phi_{S} > 0.57$) the salient mechanical properties such as arching and slow dense flow are determined by the inhomogeneous internal stress fields [Jaeger et al., 1996]. Small-amplitude sound propagation, coherent and multiply scattered, provides an efficient and non intrusive probe for characterizing the structure and viscoelastic properties of granular materials [Liu and Nagel, 1993; Jia et al., 1999]; however, the nonlinear elastic behaviour of the materials become progressively more important at high-amplitude wave excitation.
在致密颗粒堆积中(固相体积分数 $\phi_{S}> 0.57$),“桥” 和缓慢致密流动等突出的机械特性是由不均匀的内部应力场决定的[Jaeger 等人,1996 年]。相干和多散射的小振幅声传播为表征颗粒材料的结构和粘弹性特性提供了一种高效、非侵入性的探针[Liu 和 Nagel,1993 年;Jia 等人,1999 年];然而,在高振幅波激励下,材料的非线性弹性行为变得越来越重要。
In ordinary elastic media, finite-amplitude sound propagation has been intensively studied to understand many nonlinear acoustic effects such as cumulative wave distortion with propagation distance as well as the concept of the parametric array [Hamilton and Blackstock, 1998]. Similar to rocks [Guyer et al., 1997; Va n D e n Abeele et al., 2002] and soils [Lu, 2005; Gilcrist et al., 2007] non cohesive granular materials exhibit intense static and dynamic nonlinear behaviours, including strong acousto-elastic effects, dynamic wave hysteresis and dynamic modulus softening [Liu and Nagel, 1993; Johnson and Jia, 2005].
在寻常的弹性介质中,人们对有限振幅声传播进行了深入研究,并了解许多非线性声学效应,例如随传播距离而产生的累积波失真以及声参量阵列的概念[Hamilton 和 Blackstock,1998 年]。与岩石[Guyer 等人,1997 年;Van Den Abeele 等人,2002 年]和土壤[Lu,2005 年;Gilcrist 等人,2007 年]类似,非粘性颗粒材料也表现出强烈的静态和动态非线性行为,包括强烈的声弹性效应、动态波滞后和动态模量软化[Liu 和 Nagel,1993 年;Johnson 和 Jia,2005 年]。
Indeed the contact force network at low confining effective pressure is fragile and may be reorganized when subject to high-amplitude sound propagation [Liu and Nagel, 1993]. However, the physics underlying these nonlinear behaviours still remains unclear and the theory deduced from first-principle calculations is not available for such disordered media.
事实上,低约束有效压力下的接触力网络是脆弱的,在受到高振幅声传播时可能会重排[Liu 和 Nagel,1993]。然而,这些非线性行为背后的物理学原理仍不清楚,从第一原理计算中推导出的理论也无法用于此类无序介质。
Recently a clapping model based on the Hertz contact theory was proposed to describe wave demodulation in granular media [Tournat et al., 2004]. Such a reversible mechanism of opening and closing of contacts has been widely employed in fissured heterogeneous materials, but may be less appropriate in granular materials where irreversible rearrangements of beads and their contacts should occur during clapping, consequently loosening the contacts with neighbours.
最近,一种基于 Hertz 接触理论的拍击模型被提出来描述颗粒介质中的波解调[Tournat 等人,2004]。这种触点开闭的可逆机制已被广泛应用于裂隙异质材料中,但在颗粒材料中可能不太适用,因为在拍击过程中,珠子及其触点会发生不可逆的重新排列,从而松散与邻近材料的接触。
In this Letter, we investigate nonlinear wave-amplitude dynamics in a glass bead pack under external stress by measuring higher harmonics generated as a function of the source amplitude.
We test the applicability of the Hertz contact theory to the granular systems at moderate amplitude and determine the coefficient of nonlinearity $\beta$ both from higher harmonics generated and from acoustoelastic measurements.
The different regimes of sound-granular matter interaction are also explored in terms of reversibility. This work may provide a useful laboratory model for better understanding the large-scale field experiments such as nonlinear sediment response during strong ground motion. [Lu, 2005; Gilcrist et al., 2007].
在这封信中,我们通过测量作为源振幅的函数的高次谐波,研究了玻璃珠堆积在外部应力作用下的非线性振幅动力学。
我们测试了 Hertz 接触理论在中等振幅下对颗粒系统的适用性,并根据产生的高次谐波和声弹性测量结果确定了非线性系数 $\beta$。
$\beta$ 通常用在液体中, 定义为非线性参数 $\beta = 1 + \frac{B}{2A}$.
此外,还从可逆性的角度探讨了声-粒状物质相互作用的不同机制。这项工作可以提供一个有用的实验室模型,以便更好地理解大尺度现场实验,如强烈地质运动过程中的非线性地震响应。[Lu,2005 年;Gilcrist 等人,2007 年]。
Experiments and Results
Our dry granular media are composed of polydisperse glass beads of diameter $d = 0.6– 0.8 \text{mm}$, confined in a cylinder of diameter $60 \text{mm}$ and closed by two fitted pistons ($\phi_{S}\approx 0.63$). We apply a normal load $P_{0}$ of several hundred $\text{kPa}$ to the medium after one cycle of loadingunloading. Lengths of the cell $L$ range from $25 \text{mm}$ to $65 \text{mm}$.
我们的干燥颗粒介质由直径为 $d = 0.6- 0.8 \text{mm}$ 的多分散玻璃珠组成,这些玻璃珠被限制在一个直径为 $60 \text{mm}$ 的圆柱体中,并由两个合适的活塞封闭 ($\phi_{S}\approx 0.63$)。经过一个加载-卸载周期后,我们对介质施加几百 $\text{kPa}$ 的法向载荷 $P_{0}$。颗粒池的尺度(高度) $L$ 范围为 $25 \text{mm}$ 到 $65 \text{mm}$。
A broadband source transducer of diameter $30 \text{mm}$ and an identical detecting transducer are placed on the axis, respectively, at the top and bottom of the cell in direct contact with glass beads. A ten-cycle tone burst excitation centered at $f (= \omega/2\pi) = 50 \text{kHz}$ is applied to the source transducer.
At low frequency ($\lambda\gg d$) as in this work, longitudinal waves undergo coherent propagation. By using an impedance matched power amplifier (ENI), the measured amplitude of source displacement $u_{\text{in}}$ by an optical interferometer ranges from $2.5$ to $62.5 \text{nm}$.
一个直径为 $30 \text{mm}$ 的宽频带源换能器和一个相同大小的检测传感器分别放置在小室的顶部和底部,与玻璃珠直接接触。一个以 $f (= \omega/2\pi) = 50 \text{kHz}$ 为中心的十周期音爆激励条件, 被应用到源传感器上。
在低频($\lambda\gg d$)下,纵波(Longitudinal waves)会发生相干传播。通过使用阻抗匹配的功率放大器(ENI),光学干涉仪测量到的源位移振幅 $u_{\text{in}}$ 范围为 $2.5$到 $62.5 \text{nm}$ 不等。
In Figure 1a, we present the typical transmitted waveform detected at a distance of $64 \text{mm}$ under the confining pressure $P_{0} = 720 \text{kPa}$. The sound velocity is measured as $c_{0} = 900 \text{m/s}$ by the time of flight, and the source amplitude is $u_{\text{in}}\approx 62.5\text{nm}$ corresponding to the dynamic strain $\varepsilon_{\text{in}}(=\omega u_{\text{in}}/c_{0})\approx 2\times 10^{-5}$.
To study the generation of higher harmonics, we band-pass filtered the output signal using a temporal numerical filter centred at $50 \text{kHz}$, $2 \times 50 \text{kHz}$ and $3 \times 50 \text{kHz}$, respectively (Figures 1b – 1d).
在图 1a 中,我们展示了在约束压力 $P_{0} = 720 \text{kPa}$ 条件下,在 $64 \text{mm}$ 距离处检测到的典型透射波形。通过飞行时间测得声速为 $c_{0} = 900 \text{m/s}$,声源振幅为 $u_{\text{in}}\approx 62.5\text{nm}$ ,对应于动态应变 $\varepsilon_{\text{in}}(=\omega u_{\text{in}}/c_{0})\approx 2\times 10^{-5}$。
为了研究高次谐波的产生,我们分别使用以 $50 \text{kHz}$ 、$2 \times 50 \text{kHz}$ 和 $3 \times 50 \text{kHz}$ 为中心的时域数字滤波器对输出信号进行带通滤波(图 1b - 1d)。
The amplitudes of the fundamental, second harmonic are then measured as a function of the source amplitude $\epsilon_{\text{in}}$. These data fit well a linear and quadratic power-law dependence on $\epsilon_{\text{in}}$ (solid lines) over our experimental range, as illustrated on log-scale in Figure 1 (insets). The third harmonic is present, but the data is much scattered because of poor signal/noise ratio (not shown).
然后测量基波、二次谐波的振幅,作为源振幅 $\varepsilon_{\text{in}}$ 的函数。在我们的实验范围内,这些数据与 $\epsilon_{\text{in}}$ (实线)的线性和二次幂律关系十分吻合,如图 1(插图)中的对数标度所示。)三次谐波是存在的,但由于信噪比较差,数据非常分散(未显示)。
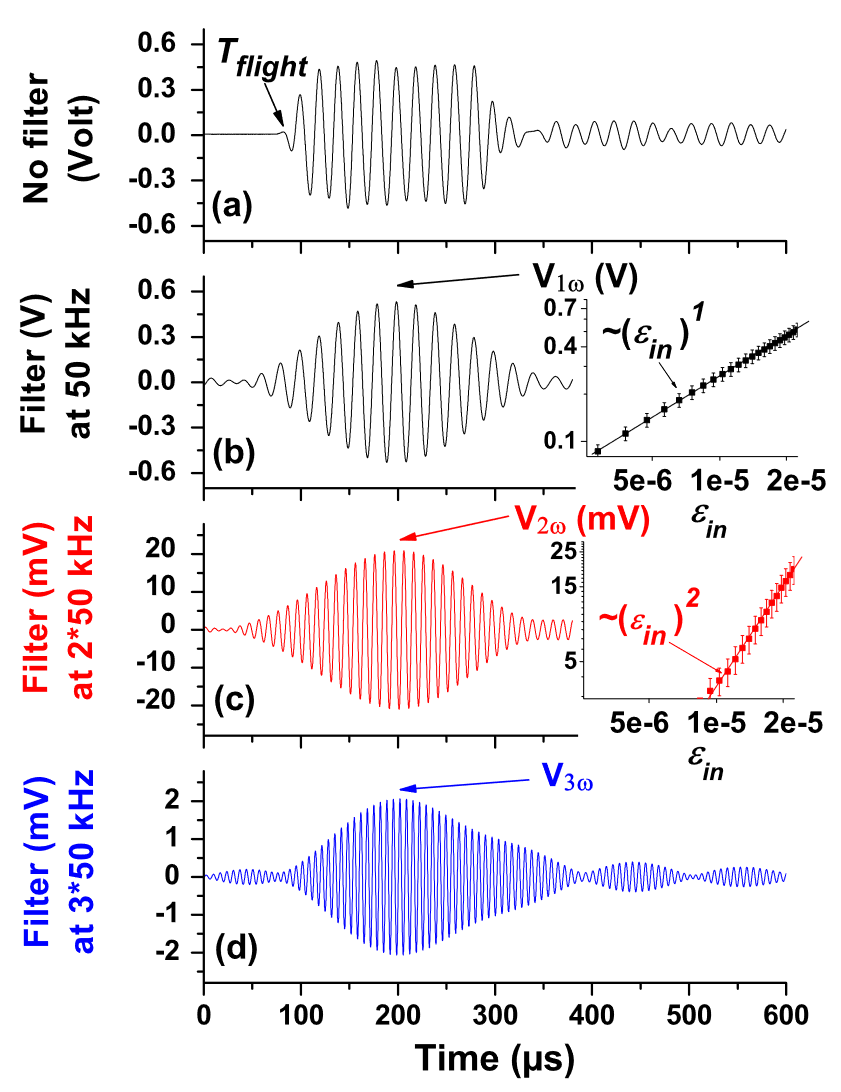
(a) Transmitted ultrasonic wave-trains and the filtered, (b) fundamental component $V_{1\omega}$, (c) second harmonic $V_{2\omega}$ and (d) third harmonic $V_{3\omega}$ under $P_{0} = 720 \text{kPa}$. Inset: Amplitudes $V_{1\omega}, V_{2\omega}$ versus $\varepsilon_{\text{in}}$.
(a) 传输的超声波列, 和滤波后的(b) 基波分量 $V_{1\omega}$, (c)二次谐波 $V_{2\omega}$, 和 (d) 三次谐波 $V_{3\omega}$.
(外加)压强 $P_{0} = 720 \text{kPa}$. 插图为振幅 $V_{1\omega}, V_{2\omega}-\epsilon_{\text{in}}$.
This test, together with the attenuation measurements described below (Figure 3), demonstrates a classic nonlinear behaviour like that observed in ordinary elastic materials, although much larger in magnitude, and ensure that the nonlinearity from the parasite sources (e.g. electrical equipment) is negligible in our experiments. Over the amplitude range shown in Figure 1, no amplitude hysteresis is observed when $\epsilon_{\text{in}}$ is increased and subsequently decreased, pointing to a reversible process.
该测试与下文所述的衰减测量(图 3)一起,展示了与普通弹性材料类似的典型非线性行为,尽管幅度要大得多,并确保在我们的实验中,来自寄生源(如电气设备)的非线性可以忽略不计。在图 1 所示的振幅范围内,当 $\epsilon_{\text{in}}$ 增大然后减小时,没有观察到振幅滞后现象,这表明这是一个可逆过程。
We next investigate the nonlinear behaviour evolution of the granular medium as we decrease the confining pressure $P_{0}$. Figure 2 shows that the fundamental and the second-harmonic amplitudes depart significantly from the linear or quadratic dependence on $\epsilon_{\text{in}}$ above a threshold depending on $P_{0}$.
For $P_{0} = 180 \text{kPa}$ the deviation from the classical scaling of the power-law (Figures 2a and 2b) is observed at $\epsilon_{\text{in}} \approx 7.5\times 10^{-6}$.
接下来我们研究颗粒介质在降低约束压力 $P_{0}$ 时的非线性行为演变。图 2 显示,在超过了取决于 $P_{0}$ 的阈值时,基波和二次谐波振幅明显偏离了与 $\varepsilon_{\text{in}}$ 的线性/二次相关性。
对于 $P_{0} = 180 \text{kPa}$,经典幂律比例的偏离(图 2a 和 2b)出现在 $\varepsilon_{\text{in}}\approx 7.5\times 10^{-6}$.
A small compaction induced of about $20 \mu \text{m}$ is also simultaneously detected by a sensor with $1 \mu\text{m}$ in resolution above this threshold (Figure 2c). This observation indicates the irreversible nature of the nonlinear behaviour in this amplitude range.
The same experiments were conducted for $P_{0} = 90 \text{kPa}$ and $P_{0} = 360 \text{kPa}$ where transition occurs around $\epsilon_{\text{in}} \approx 4.5\times 10^{-6}$ and $12\times 10^{-6}$, respectively.
在此阈值之上,分辨率为 $1 \mu \text{m}$ 的传感器也能同时检测到约 $20 \mu \text{m}$ 的小压实(图 2c)。这一观察结果表明了非线性行为在这一振幅范围内的不可逆性质。
对 $P_{0} = 90 \text{kPa}$ 和 $P_{0} = 360 \text{kPa}$ 进行了同样的实验,转变分别发生在 $\varepsilon_{\text{in}} \approx 4.5\times 10^{-6}$ 和 $12 \times 10^{-6}$ 。
In terms of the static compression $\epsilon_{0}$(~$P_{0}^{2/3}$ according to the Hertz elasticity, see below), the threshold $\epsilon_{\text{in}}$ corresponds roughly to a dimensionless ratio $r_{s} = \epsilon_{\text{in}}/\epsilon_0$ of about $3$%.
These results suggest a possible transition diagram as a function of $r_{s}$ (Figure 2c, inset) between two distinct regimes of soundmatter interaction.
就静态压缩 $\varepsilon_{0}$(根据 Hertz 弹性原理,约为 $P_{0}^{2/3}$, 见下文)而言,阈值 $\varepsilon_{\text{in}}$ 大致相当于无量纲比率 $r_{s} = \varepsilon_{\text{in}}/\varepsilon_{0}\approx 3\%$.
这些结果表明,作为 $r_{s}$ 的函数,声-物质相互作用的两种不同机制之间可能存在过渡相(图 2c,插图)。
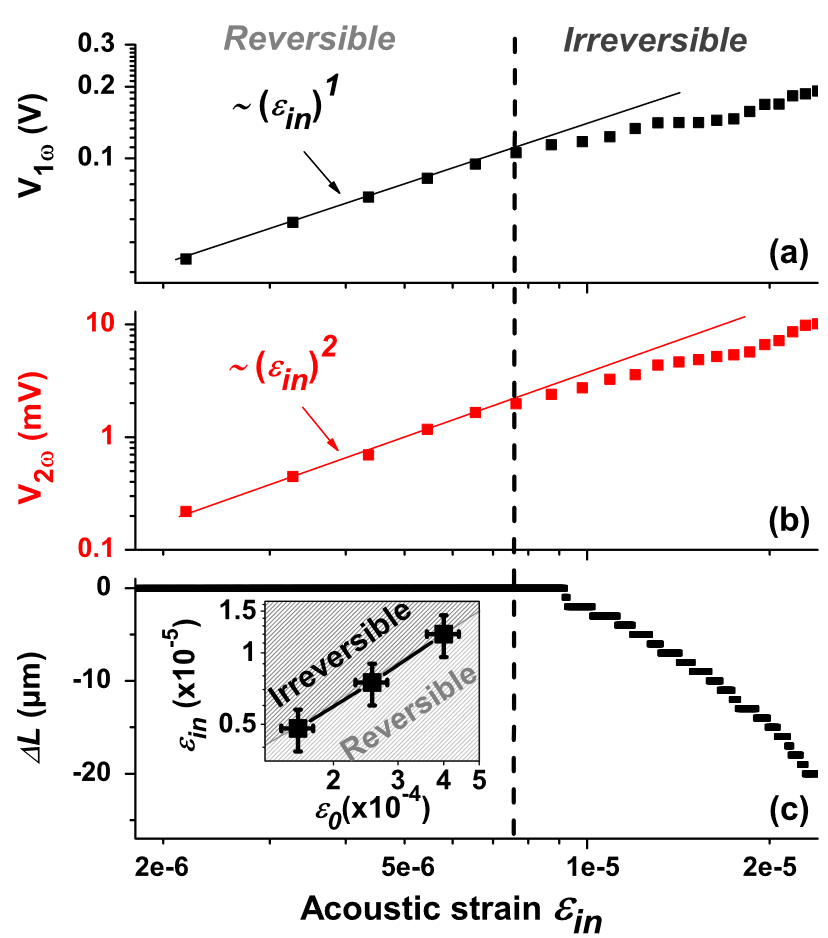
(a) Fundamental component $V_{1\omega}$ and (b) second harmonic $V_{2\omega}$ amplitudes vs source amplitude $\epsilon_{\text{in}}$ under $P_{0} = 180 \text{kPa}$, together with (c) the sample height variation $\Delta L$. Solid lines correspond to classical nonlinear predictions. Inset: transition diagram $\epsilon_{\text{in}}$ vs $\epsilon_{0}$.
(a) 在 $P_{0} = 180 \text{kPa}$ 条件下,基波分量 $V_{1\omega}$ 和 (b) 二次谐波 $V_{2\omega}$ 振幅与源振幅 $\varepsilon_{\text{in}}$,以及 (c) 样本高度变化 $\Delta L$。实线对应经典非线性预测。插图:$\epsilon_{\text{in}}$ vs $\epsilon_{0}$ 过渡相。
Analysis and Discussion
In order to interpret the nonlinear behaviour observed in the reversible regime, we analyze our results with a meanfield model based on the Hertz contact nonlinearity. Denote $\sigma_{a}$ and $\epsilon_{a}$ as dynamic stress and strain, respectively, the stress-strain relation can be expressed by
$$ \sigma_{a} = K_{0}\epsilon_{a}(1 + \beta\epsilon_{a} + \dots) + \eta\frac{\partial \epsilon_{a}}{\partial t} $$
where $K_{0}$ is the linear dynamic modulus related to the sound velocity $c_{0} = \sqrt{K_{0}/\rho_{0}}$, and $\beta$ is the coefficient of nonlinearity also termed as the third-order elastic constant the principal measure of the finite-amplitude distortions associated with the sound propagation.
为了解释在可逆体系中观察到的非线性行为,我们使用基于 Hertz 接触非线性的平均场模型来分析我们的结果。将 $\sigma_{a}$ 和 $\varepsilon_{a}$ 分别表示动态应力和应变,应力-应变关系可表示为
$$ \sigma_{a} = K_{0}\varepsilon_{a}(1 + \beta\varepsilon_{a} + \dots) + \eta\frac{\partial \varepsilon_{a}}{\partial t} $$
其中,$K_{0}$ 是与声速 $c_{0} = \sqrt{K_{0}/\rho_{0}}$ 相关的线性动态模量 ,$\beta$ 是非线性系数,也称为三阶弹性常数,是与声音传播相关的有限振幅失真的主要度量。
As shown below, $\beta$ can be determined by either wave mixing measurements (e.g., harmonic generation) or acoustoelastic measurements. As a first approach to account for the internal dissipation in the granular medium, we add a loss term via $\eta$, akin to the viscosity in fluids, which leads to the Burgers equation -the most widely used model equation for studying the combined effects of attenuation and nonlinearity on progressive plane waves [Hamilton and Blackstock, 1998]:
$$ \mathbf{\rho}_{0}\frac{\partial^{2}u}{\partial t^{2}} - \mathbf{\eta}\frac{\partial^{3}u}{\partial a^{2}\partial t} - \mathbf{\rho}_{0}c_{0}^{2}\frac{\partial^{2}u}{\partial a^{2}} - 2\mathbf{\rho}_{0}c_{0}^{2}\mathbf{\beta}\left(\frac{\partial u}{\partial a}\right)\left(\frac{\partial^{2} u}{\partial a^{2}}\right) = 0 $$
where $\rho_{0}$ is the medium density and $a$ is the material coordinate.
如下所示,$\beta$ 可以通过混波测量(如谐波发生)或声弹性测量来确定。作为解释颗粒介质内部耗散的第一种方法,我们通过 $\eta$ 增加一个损耗项,类似于流体中的粘度,从而导出 Burgers 方程–这是研究衰减和非线性对渐进平面波的综合影响时最广泛使用的模型方程[Hamilton 和 Blackstock, 1998]:
$$ \mathbf{\rho}_{0}\frac{\partial^{2}u}{\partial t^{2}} - \mathbf{\eta}\frac{\partial^{3}u}{\partial a^{2}\partial t} - \mathbf{\rho}_{0}c_{0}^{2}\frac{\partial^{2}u}{\partial a^{2}} - 2\mathbf{\rho}_{0}c_{0}^{2}\mathbf{\beta}\left(\frac{\partial u}{\partial a}\right)\left(\frac{\partial^{2} u}{\partial a^{2}}\right) = 0 $$
其中 $\rho_{0}$ 是介质密度,$a$ 是材料坐标。
Introducing the Gold’berg number $\Gamma = l_{A}/l_{S}$ defined as the ratio of the attenuation length to the shock distance, we can obtain the approximate expressions for the displacement fields in the limiting case of weak waves dominated by the attenuation process $(\Gamma < 1)$. Remember that $l_{A} = 1/\alpha$ where $\alpha$ is the linear coefficient of attenuation and $l_{S} = 1/(\beta k\epsilon_{\text{in}})$ where $k$ is the wave number.
引入 Gold’berg 数 $\Gamma = l_{A}/l_{S}$, 定义为衰减长度与冲击距离之比,我们可以得到在衰减过程 $(\Gamma < 1)$ 主导的弱波极限情况下位移场的近似表达式。记住 $l_{A} = 1/\alpha$, 其中 $\alpha$ 是线性衰减系数,$l_{S} = 1/(\beta k\varepsilon_{\text{in}})$, 其中 $k$ 是波数。
If the distance of propagation $a$ is comparable or larger than $l_{A}$(i.e., $a\alpha\geq 1$), the displacements of the fundamental, second and third harmonic components can be further simplified, as:
$$ \begin{cases} u_{1\omega}(a,t) \approx u_{\text{in}}e^{-a\alpha}\cos{(ka-\omega t)}\\ \\ u_{2\omega}(a,t) \approx \frac{u_{\text{in}}^{2}}{8}\left(\frac{\beta\omega^{2}}{\alpha c_{0}^{2}}\right)e^{-2\alpha a}\cos{[2(ka-\omega t)]}\\ \\ u_{3\omega}(a,t) \approx \frac{u_{\text{in}}^{3}}{48}\left(\frac{\beta\omega^{2}}{\alpha c_{0}^{2}}\right)^{2}e^{-3\alpha a}\cos{[3(ka-\omega t)]} \end{cases} $$
with $\alpha = \eta\omega^{2}/(2\rho_{0}c_{0}^{3})$. Notice that the approximate expressions given in equation (3) would have a more general use which is not limited by the specific loss model in equation (1) [McCall, 1994], provided that $\alpha$ is determined independently, e.g., by measurements.
如果传播距离 $a$ 与 $l_{A}$ 相当或大于 $l_{A}$(即 $a\alpha\geq 1$),则基波、二次谐波和三次谐波分量的位移可以进一步简化为:
$$ \begin{cases} u_{1\omega}(a,t) \approx u_{\text{in}}e^{-a\alpha}\cos{(ka-\omega t)}\\ \\ u_{2\omega}(a,t) \approx \frac{u_{\text{in}}^{2}}{8}\left(\frac{\beta\omega^{2}}{\alpha c_{0}^{2}}\right)e^{-2\alpha a}\cos{[2(ka-\omega t)]}\\ \\ u_{3\omega}(a,t) \approx \frac{u_{\text{in}}^{3}}{48}\left(\frac{\beta\omega^{2}}{\alpha c_{0}^{2}}\right)^{2}e^{-3\alpha a}\cos{[3(ka-\omega t)]} \end{cases} $$
其中 $\alpha = \eta\omega^{2}/(2\rho_{0}c_{0}^{3})$.
请注意,等式 (3) 中给出的近似表达式具有更广泛的用途,不受等式 (1) 中特定损耗模型的限制 [McCall, 1994],前提是 $\alpha$ 是独立确定的,比如测量得到。
To this end, we measure the amplitudes of the transmitted signals ($V_{1\omega}$) as a function of distance $a$ at small-amplitude input for different frequency $f$. As shown in Figure 3 (inset), the amplitude dependences are linear in the semi-logarithmic scale and the slopes of the straight lines provide the linear attenuation coefficients $\alpha(f)$. The same measurements of a are conducted in the nonlinear regime with the second and third harmonics, respectively.
为此,我们测量了在不同频率 $f$ 的小振幅输入下,传输后信号的振幅($V_{1\omega}$)与距离 $a$ 的函数关系。如图 3(插图)所示,振幅在半对数范围内呈线性关系,并且直线的斜率提供了线性衰减系数 $\alpha(f)$。在非线性系统中,分别用二次谐波和三次谐波对 $\alpha$ 进行了相同的测量。
Several results are given in Figure 3 (table). The observation that $\alpha_{2*50\text{kHz}} \neq \alpha_{100\text{kHz}}$ and $\alpha_{3*50\text{kHz}} \neq \alpha_{150\text{kHz}}$ confirms that the harmonic generation observed in our experiments arises within the granular medium and not from the parasite sources originating at the input level.
Moreover, the data show that $\alpha_{2*50\text{kHz}} \approx 2\alpha_{50\text{kHz}}$ and $\alpha_{3*50\text{kHz}} \approx 3\alpha_{50\text{kHz}}$, which is reasonably in agreement with the predictions of equations (3) and consequently supports the validity of the present model.
图 3(表格)给出了一些结果。观察发现,$\alpha_{2*50\text{kHz}} \neq \alpha_{100\text{kHz}}$ 和 $\alpha_{3*50\text{kHz}} \neq \alpha_{150\text{kHz}}$ 证实了我们的实验中观察到的谐波产生是在颗粒介质中产生的,而不是来自输入层的寄生源。
此外,数据显示 $\alpha_{2*50\text{kHz}} \approx 2\alpha_{50\text{kHz}}$ 和 $\alpha_{3*50\text{kHz}} \approx 3\alpha_{50\text{kHz}}$, 这与方程(3)的预测是合理一致的,因此支持了本模型的有效性。
For $f = 50 \text{kHz}$ the attenuation length $l_{A}$ is about $45 \text{mm}$; the observation of second-harmonic growth occurring principally within $a < 10 \text{mm}$ is difficult, if not impossible, with our granular samples for $a/d$ is only about $15$ (Figure 3, inset).
Note that the understanding of the internal dissipation mechanism in the granular medium still remains incomplete; it most likely depends on the interplay between frictional, viscoelastic and scattering losses [Brunet et al., 2008], implying a complex behaviour of $\alpha(f)$ (Figure 3).
对于 $f = 50 \text{kHz}$,衰减长度 $l_{A}$ 约为 $45 \text{mm}$;要在主要的 $a < 10 \text{mm}$ 范围内观察到二次谐波的产生非常困难甚至是不可能的,因为我们的颗粒样品的 $a/d$ 仅为约 $15$(图 3,插图)。
请注意,对颗粒介质内部耗散机制的理解仍不完整;它很可能取决于摩擦、粘弹性和散射损失之间的相互作用[Brunet 等人,2008],这意味着 $\alpha(f)$ 的行为很复杂(图 3)。
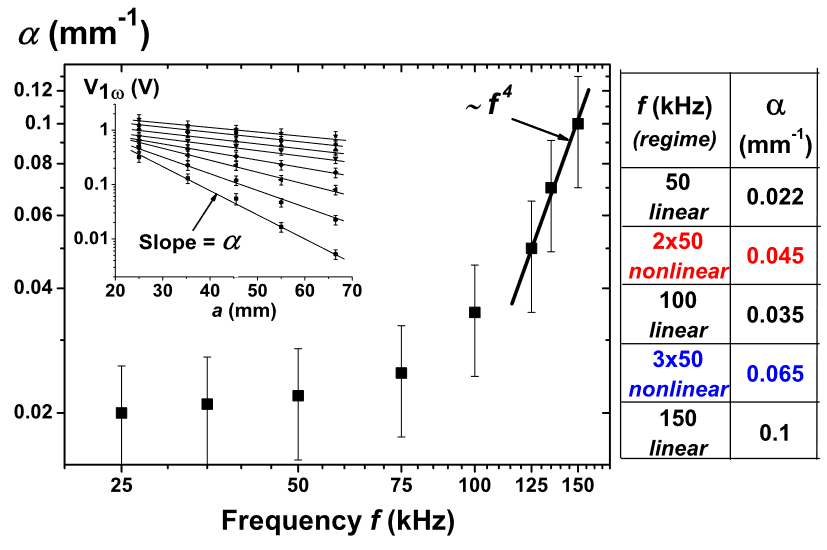
Linear attenuation coefficient $\alpha$ vs $f$. Inset: fundamental amplitudes $V_{1\omega}$ vs distance $a$ for different frequency $f$, measured under $P_{0} = 720 \text{kPa}$ with $u_{\text{in}} = 62.5 \text{nm}$. Solid lines correspond to linear fits. Table: Attenuation coefficient measured in both linear and nonlinear regimes.
线性衰减系数 $\alpha$ vs $f$。插图:在 $P_{0} = 720 \text{kPa}$ 和 $u_{\text{in}} = 62.5 \text{nm}$ 条件下测量的不同频率 $f$ 的基波振幅 $V_{1\omega}$ 与距离 $a$ 的关系。实线对应于线性拟合。表:在线性和非线性状态下测量的衰减系数。
With the attenuation $\alpha$ measured in the granular packing under $P_{0} = 720 \text{kPa}$, we can deduce the coefficient of nonlinearity $\beta$ from the ratio of measured second-harmonic amplitude to fundamental one shown in Figures 1b and 1c (insets), $V_{2\omega}/V_{1\omega} (=u_{2\omega}/u_{1\omega})$ according to equations (3a) and (3b).
The difficulty of the wave mixing method is that an independent measurement of $u_{\text{in}}$ is required. If the displacement of the source transducer measured at its free surface is considered, we obtain $\beta_{\text{WM}}\approx 3000$. This gives a shock wave distance $l_{S}$ of about few meters much larger than $l_{A}$, verifying the condition $\Gamma < 1$ assumed.
通过在颗粒堆积中 $P_{0} = 720 \text{kPa}$ 条件下测得的衰减 $\alpha$,我们可以根据公式 (3a) 和 (3b),从图 1b 和 1c(插图)所示的测得的二次谐波振幅与基波振幅之比 $V_{2\omega}/V_{1\omega} (=u_{2\omega}/u_{1\omega})$ 中推导出非线性系数 $\beta$。
混波法的难点在于需要独立测量 $u_{\text{in}}$。如果考虑在自由表面测量源传感器的位移,我们可以得到 $\beta\approx 3000$。这就得出了冲击波距离 $l_{S}$ 约为几米,远大于 $l_{A}$, 验证了假设的条件 $\Gamma_{\text{WM}} < 1$。
The most commonly used and the most precise method for determining $\beta$ is based on the acoustoelastic effect, namely velocity measurement, in which the application of a static stress $P_{0}$ change the velocity $c_{0}$ of small-amplitude sound waves as $\beta_{\text{AE}} = (\rho_{0}/2)(\mathrm{d}c_{0}^{2}/\mathrm{d}P_{0})$. Figure 4 displays the sound velocity measured by a time-of-flight method as a function of the applied stress.
确定 $\beta$ 的最常用, 最精确的方法是基于声弹性效应,即 速度 测量,其中施加静态应力 $P_{0}$ 会改变小振幅声波的速度 $c_{0}$,即 $\beta_{\text{AE}} = (\rho_{0}/2)(\mathrm{d}c_{0}^{2}/\mathrm{d}P_{0})$ 。图 4 显示了用飞行时间法测量的声速与外加应力的函数关系。
The power-law scaling $c_{0}$
$P_{0}^{0.15}$ agrees well with the prediction by the Hertz theory $c_{0}$$P_{0}^{1/6}$ [Jia et al., 1999]. The coefficient of nonlinearity $\beta_{\text{AE}}$ is then deduced by differentiating the sound velocity. The results shown in Figure 4 reveal a reasonably good agreement between measured $\beta_{\text{AE}}$ and the predicted $\beta_{\text{Hertz}} = 1/(4\epsilon)$ [Norris and Johnson, 1997], thus confirming the primary role of the Hertz nonlinearity in the granular nonlinear elasticity.Furthermore $\beta_{\text{AE}}\approx 350$ measured at $P_{0} = 720\text{kPa}$ gives $\beta_{\text{WM}}\approx 8\beta_{\text{AE}}$. The discrepancy between $\beta$ values obtained by the two methods is also reported in sedimentary rocks [D’Angelo et al., 2004].
幂律比例 $c_{0}$$P_{0}^{0.15}$ 与赫兹理论的预测值 $c_{0}$$P_{0}^{1/6}$ 非常吻合[Jia 等人,1999]。非线性系数 $\beta_{\text{AE}}$ 可以通过对声速微分推导出来。图 4 中显示的结果表明,测量值 $\beta_{\text{AE}}$ 与预测值 $\beta_{\text{Hertz}} = 1/(4\varepsilon)$ [Norris and Johnson, 1997]之间存在相当好的一致性,从而证实了赫兹非线性在颗粒非线性弹性中的主要作用。
此外,在 $P_{0} = 720\text{kPa}$ 条件下测量的 $\beta_{\text{AE}}\approx 350$,得出的 $\beta_{\text{WM}}\approx 8\beta_{\text{AE}}$。沉积岩中也出现了两种方法得到的 $\beta$ 值之间的差异[D$^{\prime}$Angelo 等人,2004 年]。
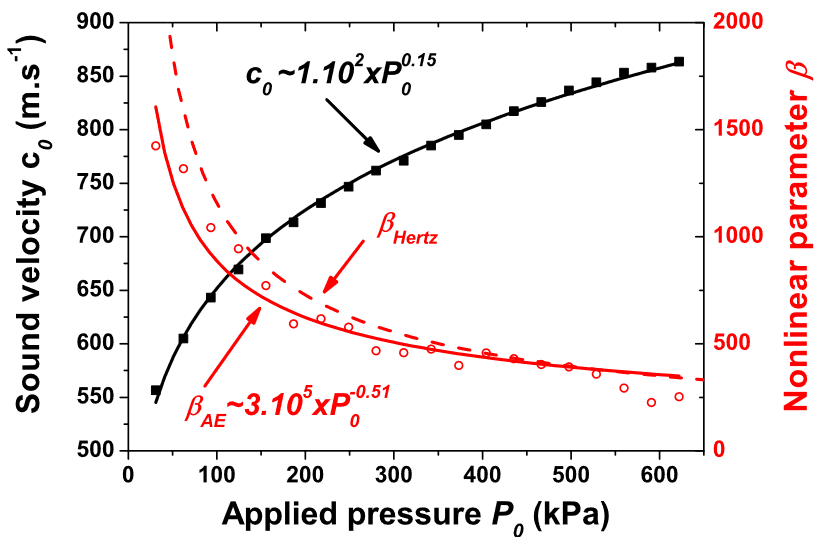
Solid squares are sound velocity $c_{0}$ measured vs $P_{0}$, and open circles are $\beta_{\text{AE}}$ deduced from velocity measurements. Solid lines correspond to power law fits and dashed line refers to calculated values $\beta_{\text{Hertz}}$ from the Hertz contact model.
实心方块是测量到的声速 $c_{0}$ 与 $P_{0}$ 的关系,空心⚪是根据速度测量值推导出的 $\beta_{\text{AE}}$。实线为幂律拟合值,虚线为 Hertz 接触模型的计算值 $\beta_{\text{Hertz}}$。
Let us finally examine the irreversible regime lower confining pressure. In Figure 5, the fundamental component and second harmonics demonstrate non-classical behaviours, i.e. amplitude hysteresis and the important deviation of the source-amplitude $\epsilon_{\text{in}}$ dependence from the classical scaling laws illustrated in Figure 1.
The scaling with $\epsilon_{\text{in}}$ in our experiments is not determinate and depends strongly on the confining pressure and the sample preparation procedure. The observation of such amplitude dynamics is similar to those in previous experiments [Liu and Nagel, 1993], and clearly reveals that there is no evidence for a scaling law such as $\epsilon_{\text{in}}^{3/2}$ for the second harmonic generation, predicted by the clapping model [Tournat et al., 2004].
最后,让我们来研究一下较低约束压力下的不可逆机制。在图 5 中,基波分量和二次谐波显示出非经典行为,即振幅滞后和源振幅 $\varepsilon_{\text{in}}$ 与图 1 所示经典比例规律的重要偏差。
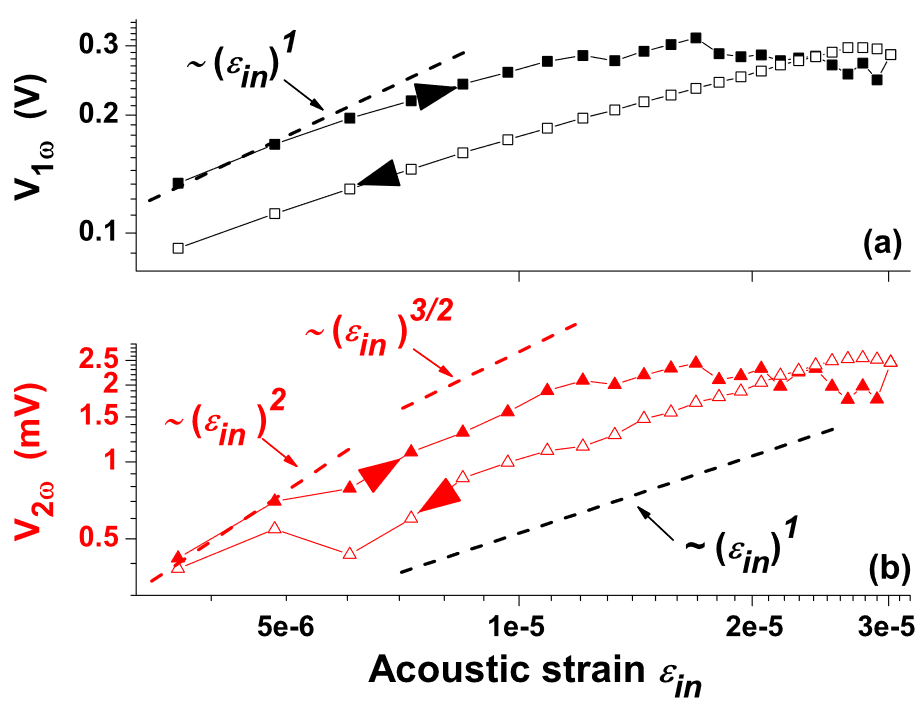
(a) Fundamental and (b) second-harmonic amplitudes vs source amplitude $\varepsilon_{\text{in}}$ under $P_{0} = 90 \text{kPa}$. The curves correspond to increasing $\varepsilon_{\text{in}}$ (solid symbols) and subsequently decreasing $\varepsilon_{\text{in}}$ (open symbols).
(a) 在 $P_{0} = 90 \text{kPa}$ 条件下,基波和(b)二次谐波振幅与源振幅 $\varepsilon_{\text{in}}$ 的关系。曲线对应于 $\varepsilon_{\text{in}}$(实心符号)的增大和随后 $\varepsilon_{\text{in}}$(开口符号)的减小。)
在我们的实验中,$\varepsilon_{\text{in}}$ 的比例并不确定,而且在很大程度上取决于约束压力和样品制备过程。对这种振幅动态的观察与之前的实验[Liu 和 Nagel, 1993]类似,并清楚地揭示了没有证据表明拍击模型(Clapping Model)[Tournat 等人,2004]所预测的二次谐波生成存在 $\varepsilon_{\text{in}}^{3/2}$ 这样的比例规律。
In fact, the reversible nature of such a mechanism is inconsistent with the observed hysteretic behaviour and the irreversible compaction induced in this regime.
Notice, however, the characteristic length scale associated with this small plastic deformation is different from that observed in a tapping experiment [Nowak et al., 1998].
Instead, it is probably related to frictional dynamics at the grain contact level, leading to the onset of the micro-arrangement of asperities between rough spheres and resulting in a softening of elastic modulus and a change in the morphology of the contact networks (to be detailed elsewhere).
事实上,这种机制的可逆性与所观察到的滞后行为和在此机制下诱发的不可逆压实是不一致的。
然而,请注意,与这种小塑性变形相关的特征长度尺度不同于在按压实验中观察到的长度尺度[Nowak 等人,1998 年]。
相反,它很可能与颗粒接触层面的摩擦动力学有关,导致粗糙球体之间的尖晶微排列的开始,并导致弹性模量的软化和接触网络形态的改变(将在别处详细说明)。
This picture is consistent with the observed small threshold value $r_{s}$ of a few percent. We believe that our work bridges the nonlinear sound-matter interaction described here and the recent concept of effective granular temperature (energy injected by vibration) proposed in the jamming transition process.
这与观测到的几个百分点的小阈值 $r_{s}$ 是一致的。我们相信,我们的工作将此处描述的非线性声物质相互作用与最近在堵塞转变过程中提出的有效颗粒温度(振动注入的能量)概念联系起来。
Conclusions
In summary, we have identified two regimes of nonlinear elastic behaviour in a confined granular medium stemming from the nonlinear dynamics at the grain contacts. At moderate amplitudes we find a reversible process of the sound-material interaction where the second and third harmonic generation agree with the granular elasticity predicted by the Hertz contact theory. In this regime, sound speed measurements allow us to determine the coefficient of nonlinearity $\beta$ in agreement with the model.
总之,我们确定了约束颗粒介质中的两种非线性弹性行为,这些行为源于颗粒接触处的非线性动力学。在中等振幅下,我们发现声物质相互作用的可逆过程,其中二次谐波和三次谐波的产生与 Hertz 接触理论预测的颗粒弹性一致。在这个区域,声速测量允许我们确定非线性系数 $\beta$,且与模型一致。
Beyond threshold amplitude corresponding to $r_{s}$ about a few percent, the irreversible process of sound-matter interaction commences and the pure Hertz model is no longer valid. Our experiments show that interpretations based only on the Hertzian nonlinear elasticity are incomplete for describing the granular nonlinear dynamics, and the frictional dynamics at the grain contact level should be included [Nihei et al., 2000]. In studies of strong ground motion, it is clear that these hysteretic behaviours may play an important role; however, the effects of grain’s shape and size dispersion as well as lower confining pressure condition should be considered in the future work.
当超过与 $r_{s}$ 几个百分点相对应的阈值振幅时,声-物质相互作用的不可逆过程开始,纯 Hertz 模型不再有效。我们的实验表明,仅基于 Hertz 非线性弹性的解释对于描述颗粒非线性动力学是不完整的,还应该包括颗粒接触层面的摩擦动力学[Nihei 等人,2000]。在剧烈地质运动研究中,这些滞回行为显然可能发挥重要作用;不过,在今后的工作中应考虑颗粒形状和尺寸分散以及较低约束压力条件的影响。

