Abstract
The linear and nonlinear elastic properties of granular media are analyzed within the context of effective medium theories, as well as with numerical molecular dynamic simulations, assuming the validity of the Hertz-Mindlin theory at the single contact level.
There is a crucial distinction between force laws which are path independent, leading to a hyper-elastic effective medium theory, and those which are path dependent, for which the deformation history must be followed explicitly.
假定 Hertz-Mindlin 理论在单接触层面上有效,在有效介质理论以及分子动力学数值模拟的背景下分析了颗粒介质的线性和非线性弹性的特性。
与路径无关的力定律和与路径相关的力定律之间存在着关键的区别,前者导致了超弹性有效介质理论,而后者则必须明确地遵循变形历史。
The effective medium theories provide a reasonable description of existing experimental data, considered as a function of applied stress, but there are significant discrepancies. Numerical simulations resolve the question as to whether the problem lies with the treatment of the individual grain-grain contact or with the effective medium approximation (ema).
We find that the problem lies principally with the latter: The bulk modulus is well described by the ema but the shear modulus is not, principally because the ema does not correctly allow for the grains to relax from the affine motion assumed by the ema.
有效介质理论合理地描述了作为外加应力函数的现有实验数据,但存在显著差异。数值模拟解决了是单个颗粒-颗粒接触处理方法的问题还是有效介质近似(ema)的问题。
我们发现问题主要在于后者:体积模量可以用 ema 很好地描述,但剪切模量却不能,这主要是因为 ema 没有正确地允许颗粒从 ema 假设的仿射运动中弛豫下来。
Introduction
The elastic properties of granular aggregates, such as sedimentary rocks, can be enormously nonlinear as compared with the properties of nonporous materials. The end member of such systems may be taken to be a loose/unconsolidated aggregate of glass beads which acquire a stiffness solely as a result of applied stress.
This is because if two grains are just touching, the force, considered as a function of displacement, does not initially grow linearly, as with most systems, but it has a power law behavior (Eqs. (1) and (2) below).
与无孔材料的特性相比,沉积岩等颗粒集合体的弹性特性可能极其非线性。此类系统的终端部件可以看作是由玻璃珠组成的松散/未固结的集合体,其刚度完全是外加应力的结果。
这是因为,如果两粒玻璃珠恰好接触,被考虑为位移函数的力最初并不像大多数系统那样线性增长,而是具有幂律行为(下文公式 (1) 和 (2))。
Aside from posing an interesting problem in the physics of disordered systems, these systems are unusually nonlinear in their response and they can exhibit path dependence.
By this we mean that the work done in deforming the system can depend upon whether one first compresses the system, then shears it, or first shears then compresses, or compresses and shears simultaneously, etc. The result depends upon the path taken in $\{\varepsilon_{ij}\}$ space and not just on the final state of strain $\{\varepsilon_{ij}(\text{final})\}$.
除了在无序系统物理学中提出了一个有趣的问题之外,这些系统的反应还具有非同寻常的非线性,它们可以表现出路径依赖性。
我们的意思是,系统变形所做的功取决于是先压缩系统,然后再剪切,还是先剪切后压缩,还是压缩和剪切同时进行,等等。结果取决于在 ${\varepsilon_{ij}}$ 空间中的路径,而不仅仅取决于应变的最终状态 ${\varepsilon_{ij}(\text{final})}$。
Here, we review some recent theoretical research we have undertaken in an attempt to understand these systems. We first discuss effective medium theories of the elastic properties, then we present our molecular dynamic simulations, and we end with a brief summary.
在此,我们回顾了最近为了解这些系统而开展的一些理论研究。我们首先讨论弹性特性的有效介质理论,然后介绍我们的分子动力学模拟,最后进行简要总结。
Effective medium theories
The starting point is the behavior of a single grain-grain contact, which we assume to be describable by the Hertz-Mindlin theory and variations thereof. Two touching grains are displaced in compression along a line joining their centers by an amount $2w$. They may also suffer a transverse relative displacement of their centers by an amount $2s$, holding their rotational orientation fixed for the moment.
The normal and transverse forces, $\mathbf{f}_{n}$ and $\mathbf{f}_{t}$ may be written in terms of $w$ and $s$. The idea is that as two spheres are pressed together the circle of contact continuously grows; the result is that the contact becomes increasingly stiffer with respect to further compression.
我们以单个颗粒-颗粒接触的行为为出发点,假定它可以用 Hertz-Mindlin 理论及其变式来描述。两个接触的颗粒在压缩过程中沿着连接其中心的直线发生位移,位移量为 $2w$。它们的中心还可能发生横向相对位移,位移量为 $2s$,此时它们的旋转方向保持不变。
法向力和横向力 $\mathbf{f}_{n}$ 和 $\mathbf{f}_{t}$ 可以用 $w$ 和 $s$ 来表示。其原理是,当两个球体被压在一起时,接触圆不断增大;其结果是,相对于进一步的压缩,接触变得越来越坚硬。
Similarly, it may be assumed, for example, that the contact circle is a no-slip zone. The more the spheres are pressed together, the stiffer the contact becomes with respect to transverse relative displacement of the sphere centers (assuming the spheres are not allowed to rotate). The relevant expressions relating the forces to the displacements may be written as
$$ f_{n} = \frac{2}{3}C_{n}R^{1/2}w^{3/2}, \tag{1}\label{eq1} $$ $$ \Delta f_{t} = C_{t}(Rw)^{1/2}\Delta s.\tag{2}\label{eq2} $$
The prefactors $C_{n}=4G/(1-\nu)$ and $C_{t}=8G/(2-\nu)$ are defined in terms of the shear modulus $G$ and the Poisson’s ratio $\nu$ of the individual particles. $R$ is the harmonic mean of the radii of the two spheres.
同样,也可以假设接触圆为无滑动区。球体压在一起越多,相对于球体中心的横向相对位移(假设球体不允许旋转),接触就越僵硬。力与位移的相关表达式可写成
$$ f_{n} = \frac{2}{3}C_{n}R^{1/2}w^{3/2},\\ \Delta f_{t} = C_{t}(Rw)^{1/2}\Delta s. $$
其中,前因子 $C_{n}=4G/(1-\nu)$ 和 $C_{t}=8G/(2-\nu)$ 以单个颗粒的剪切模量 $G$ 和泊松比 $\nu$ 定义。$R$ 是两个球体半径的调和平均值。
Eq. (2) is written in differential form to emphasize the fact that the actual value of the transverse force, $f_{t}$, depends upon the deformation path taken in $\{w,s\}$ space and not simply on the final values of $w$ and $s$. Thus $f_{t}$ depends upon the entire history of the trajectory: $f_{t} = f_{t}[\{w(\xi)\},\{s(\xi)\}]$ where $\xi$ is some conveniently chosen parameter (see Refs. [2,3] and references therein).
公式 (2) 以微分的形式书写,以强调横向力 $f_{t}$ 的实际值取决于在 $\{w,s\}$ 空间中的变形路径,而不仅仅取决于 $w$ 和 $s$ 的最终值。因此 $f_{t}$ 取决于轨迹的整个历史:$f_{t} = f_{t}[\{w(\xi)\},\{s(\xi)\}]$, 其中 $\xi$ 是某个为方便选择的参数(见参考文献 [2,3] 及其中的参考文献)。
Along a given trajectory there is no hysteresis, meaning the grain-grain contact is exactly reversible along that trajectory. But one does different amounts of work depending upon the trajectory taken; if one releases the forces along a trajectory different than the one in which they were established, there will be a net loss of energy. This behavior of a single grain-grain contact leads directly to the path dependence of the macroscopic ensemble, considered as a function of applied strain, $\{\varepsilon_{ij}\}$.
在给定的轨迹上没有滞后现象,这意味着颗粒与颗粒之间的接触在该轨迹上是完全可逆的。但是,不同的轨迹会产生不同的功,如果沿着不同的轨迹释放力,就会产生净能量损失。单个颗粒-颗粒接触的这种行为直接导致了宏观集合的路径依赖性,将其视为施加应变的函数,$\{\varepsilon_{ij}\}$。
The basic idea of the e!ective medium theories relevant to these problems is that the macroscopic work done in deforming the system is set equal to the sum of the work done on each grain-grain contact and that the latter is replaced by a suitable average. There are two assumptions: (1) The center of each grain displaces according to the dictates of the macroscopic strain tensor, $\varepsilon_{ij}$:
$$ u_{i} = \varepsilon_{ij}X_{j},\tag{3}\label{eq3} $$
where $\mathbf{X}$ is the initial position of the center of the grain. When the deformation is describable by a symmetric deformation, $\nabla\times\mathbf{u} = 0$, none of the grains rotate. This is called the “assumption of affine motion”. (2) Each grain experiences essentially the same environment as any other grain. On average, the distribution of contacts is spherically symmetric. Under these assumptions, the total work done on the system may be written in terms of angular averages of the work done on a single contact. This sort of “effective medium theory” is simpler than the conventional Bruggeman type of ema (see also Ref. [5]) in that it is more analogous to a simple average of the non-linear spring constants.
与这些问题相关的有效介质理论的基本思想是:将系统变形所做的宏观功设定为等于每个颗粒-颗粒接触所做的功之和,并用一个合适的平均值代替后者。这里有两个假设:(1) 每个颗粒的中心都根据宏观应变张量 $\varepsilon_{ij}$ 的要求进行位移:
$$ u_{i} = \varepsilon_{ij}X_{j}, $$
其中 $\mathbf{X}$ 是颗粒中心的初始位置。当变形可以用对称变形来描述时,即 $\nabla\times\mathbf{u} = 0$,颗粒都不会旋转。这被称为 “仿射运动假设”。(2) 每个颗粒与其他颗粒所处的环境基本相同。平均而言,接触分布呈球形对称。根据这些假设,系统所做的总功可以用单个接触点所做功的角度平均值来表示。这种 “有效介质理论” 比传统的 Bruggeman 类型的 ema 更简单(另见参考文献 [5]),因为它更类似于非线性弹簧常数的简单平均值。
As written, the transverse force, Eq. (2), was derived under the assumption that once the grains are pressed together, there is perfect sticking of the contact circles. This force is path dependent, meaning that whether the grains are first pressed and then sheared, or vice versa, makes a di!erence in the work done on the contact. The numerical value of $f_{t}$ depends upon the path taken in $(w, s)$ space. Were we to assume, on the other hand, that there is perfect slippage of the particles, $\mathbf{f}_{t}\equiv 0$ instead of Eq. (2), then the resulting forces are path independent.
如上文所述,公式 (2) 中的横向力是在假定一旦颗粒被压在一起,接触圆完全粘连的情况下得出的。这个力与路径有关,也就是说,颗粒是先被挤压后被剪切,还是先被剪切后被挤压,都会对接触做功产生影响。$f_{t}$ 的数值取决于在 $(w, s)$ 空间中的路径。另一方面,如果我们假设粒子完全滑动,$\mathbf{f}_{t}\equiv 0$ 而不是公式 (2),那么所产生的力与路径无关。
The practical result of this path independent assumption is that the resulting work done in deforming the system is now a function of the state of strain and is not dependent upon the way in which the strain is applied. The path independent forces lend themselves to the development of a macroscopic strain energy density, and thus to a well-defined theory of hyper-elasticity, whereas the path dependent forces need to be treated specially. We consider these two cases in turn.
这种与路径无关的假设的实际结果是,系统变形所产生的功现在是应变状态的函数,而不依赖于施加应变的方式。与路径无关的力适合于宏观应变能密度的发展,从而适合于明确定义的超弹性理论,而与路径有关的力则需要特殊处理。我们依次考虑这两种情况。
A cautionary note: In reality the contact may slip over an annular ring if the coefficient of friction is finite. In the limit of infinitesimal $\Delta s$ we either neglect the slippage altogether or we assume complete slip, as the case may be. In any case, the forces are conservative in the sense that if the deformation path, whatever it may be, is reversed exactly, the total work done is zero.
注意事项:在现实中,如果摩擦系数是有限的,接触点可能会在环形圈上滑动。在无限小 $\Delta s$ 的极限中,我们要么完全忽略滑动,要么假设完全滑动,视情况而定。在任何情况下,力都是保守的,因为如果变形路径(不管是什么路径)被完全反转,那么所做的总功为零。
Path independent forces
If the work done on a single contact is independent of the order in which the normal and transverse forces are applied, i.e. they are path independent, then the system as a whole is said to be hyper-elastic. An energy density, $U(\{\varepsilon_{ij}\})$, can be defined in terms of the macroscopic strain tensor, $\varepsilon_{ij}$, and it can usefully be expanded in powers thereof. For any isotropic system this expansion takes the form:
$$ U(\{\varepsilon_{ij}\}) = U_{0} - p\varepsilon_{ii} + \frac{1}{2}\left[K - \frac{2}{3}\mu\right]\varepsilon_{ii}^{2} + \mu\varepsilon_{ij}^{2} + \frac{1}{3}A\varepsilon_{ij}\varepsilon_{jk}\varepsilon_{ki} + B\varepsilon_{ik}^{2}\varepsilon_{ll} + \frac{1}{3}\varepsilon_{ll}^{3} + \dots.\tag{4}\label{eq4} $$
Here, $p$ is the static pressure and the strain tensor, $\varepsilon_{ij}$, is measured relative to the system in its reference state at pressure $p$.
如果在单个接触上所做的功与施加法向力和横向力的顺序无关,即与路径无关,那么整个系统就被称为超弹性系统。能量密度 $U(\{\varepsilon_{ij}\})$ 可以用宏观应变张量 $\varepsilon_{ij}$ 来定义,并且可以用它的幂来展开。对于任何各向同性系统,这种展开形式为:
$$ U(\{\varepsilon_{ij}\}) = U_{0} - p\varepsilon_{ii} + \frac{1}{2}\left[K - \frac{2}{3}\mu\right]\varepsilon_{ii}^{2} + \mu\varepsilon_{ij}^{2} + \frac{1}{3}A\varepsilon_{ij}\varepsilon_{jk}\varepsilon_{ki} + B\varepsilon_{ik}^{2}\varepsilon_{ll} + \frac{1}{3}\varepsilon_{ll}^{3} + \dots. $$
The second-order elastic constants are $K$, the bulk modulus, and $\mu$, the shear modulus; they determine the speeds of small amplitude sound:
$$ V_{p} = \sqrt{\frac{K + \frac{4}{3}\mu}{\rho}}\tag{5}\label{eq5} $$
is the compressional sound speed and
$$ V_{s} = \sqrt{\frac{\mu}{\rho}}\tag{6}\label{eq6} $$
is the shear speed. ($\rho$ is the density.) The third-order elastic constants, $A$, $B$, $C$ describe how the speeds of sound change to first order in an additional applied stress, $\Delta\sigma_{ij}$, and they also describe such nonlinear e!ects as second harmonic generation, shock wave formation, etc. For the path-independent model described above (i.e. when we set $\mathbf{f}_{t}\equiv 0$), it is straightforward to carry out this expansion to derive analytic expressions for the various moduli. Indeed, the path-independent models can be generalized slightly to include those in which the beads are first welded together over a radius $b > 0$.
二阶弹性常数是体积模量 $K$ 和剪切模量 $\mu$;它们决定了小振幅声的速度:
$$ V_{p} = \sqrt{\frac{K + \frac{4}{3}\mu}{\rho}} $$
是压缩声速,而
$$ V_{s} = \sqrt{\frac{\mu}{\rho}} $$
是剪切速度($\rho$ 是密度)。三阶弹性常数 $A$、$B$、$C$ 描述了声速如何在额外外加应力 $\Delta\sigma_{ij}$ 的作用下发生一阶变化,它们还描述了二次谐波产生、冲击波形成等非线性效应。对于上述与路径无关的模型(即当我们设置 $\mathbf{f}_{t}\equiv 0$时),进行这种扩展可以直接得出各种模量的解析表达式。事实上,路径无关模型可以稍加推广,以纳入那些球珠首先在半径 $b > 0$ 上粘连在一起的模型。
Theoretical predictions of the speeds of sound from this path-independent model for different values of $b$ are plotted in Fig. 1, taken from Ref. [2]. One of the thirdorder constants from this model is plotted in Fig. 2. (Here, the third order constants are in the ratio $A:B:C::8:4:1$ so it is necessary to plot only one of them.)
图 1 是这一与路径无关的模型对不同 $b$ 值的声速的理论预测,摘自参考文献 [2].图 2 中绘制了该模型的一个三阶常数(此处三阶常数的比例为 $A:B:C::8:4:1$,因此只需绘制其中一个常数)。
For the case in which $b=0$ (i.e. unconsolidated beads) the ema predictions can be simply expressed as functions of the pressure:
$$ K = \frac{C_{n}}{12\pi}[(1-\phi)Z]^{2/3}\left[\frac{6\pi p}{C_{n}}\right]^{1/3}, \tag{7}\label{eq7} $$ $$ \mu = \frac{C_{n}}{20\pi}[(1-\phi)Z]^{2/3}\left[\frac{6\pi p}{C_{n}}\right]^{1/3}, \tag{8}\label{eq8} $$ $$ A = -\frac{C_{n}}{70\pi}[(1-\phi)Z]^{4/3}\left[\frac{6\pi p}{C_{n}}\right]^{-1/3}. \tag{9}\label{eq9} $$
Here, $Z$ is the average coordination number and $\phi$ is the porosity.
对于 $b=0$ 的情况(即非固结球珠),ema 预测值可以简单地表示为压力的函数:
$$ \begin{aligned} K &= \frac{C_{n}}{12\pi}[(1-\phi)Z]^{2/3}\left[\frac{6\pi p}{C_{n}}\right]^{1/3},\\ \mu &= \frac{C_{n}}{20\pi}[(1-\phi)Z]^{2/3}\left[\frac{6\pi p}{C_{n}}\right]^{1/3},\\ A &= -\frac{C_{n}}{70\pi}[(1-\phi)Z]^{4/3}\left[\frac{6\pi p}{C_{n}}\right]^{-1/3}. \end{aligned} $$
这里,$Z$ 是平均配位数,$\phi$ 是孔隙率。
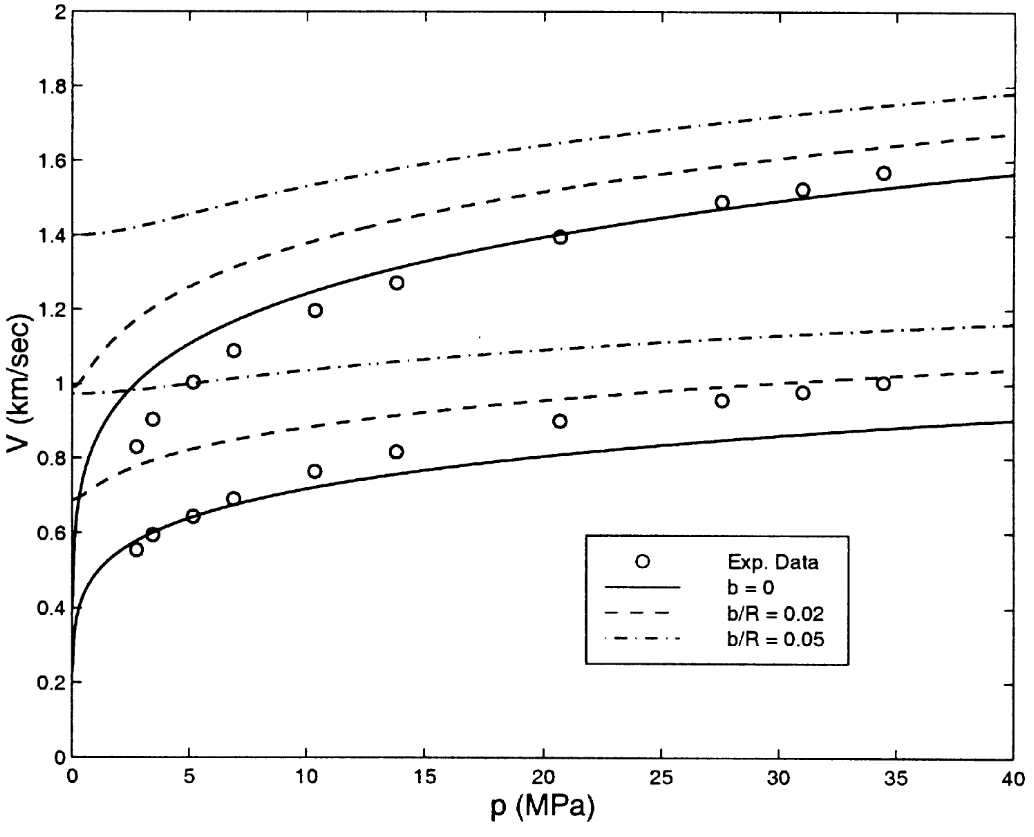
Path independent ema predictions of pressure dependent sound speeds of granular media with welded contacts. The experimental data of Domenico should be compared against the $b=0$ curves. A coordination number $Z=9$ was assumed (from Ref. [2]).
具有固连接触的颗粒介质的压力相关声速的路径无关 ema 预测。 Domenico 的实验数据应与 $b=0$ 曲线进行比较。假设配位数为 $Z=9$(来自参考文献 [2])。
From Eqs. (7)-(9) as well as from Figs. 1 and 2, we see that, for unconsolidated beads, the second-order constants decrease to zero as the confining pressure decreases to zero but the third-order (and higher) elastic constants actually diverge. It is in this sense that unconsolidated granular media can be said to be extremely nonlinear.
从公式 (7)-(9) 以及图 1 和图 2 中我们可以看出,对于未固结的球珠,二阶常数会随着约束压力的减小而减小到零,但三阶(及以上)弹性常数实际上是发散的。从这个意义上说,未固结的颗粒介质可以说是极其非线性的。
The presence of a welded contact, $b>0$, acts to cut-off the divergence, but even so these systems can be orders of magnitude more nonlinear than ordinary, non-granular materials, such as metals, glasses, plastics, etc., for which the third-order constants are of the same order of magnitude as the second.
固连接触($b>0$)的存在可截断发散,但即便如此,这些系统的非线性程度仍可能比金属、玻璃、塑料等普通非颗粒材料高出几个数量级,后者的三阶常数与二阶常数的数量级相同。
Path dependent forces
When the transverse force is given by Eq. (2), the work done in deforming the system is dependent upon the order (path) in which this is done. An expansion such as Eq. (4) therefore does not exist. Nonetheless, it is possible to develop an e!ective medium theory in which one keeps track of the order (path) in which the deformation is applied.
当横向力由式(2)给出时,系统变形所做的功取决于变形的顺序(路径)。因此,像公式 (4) 这样的展开式是不存在的。尽管如此,我们仍有可能发展出一种有效介质理论,其中我们可以追踪形变的顺序(路径)。
The resulting stress tensor, $\sigma_{ij}$, depends upon the path taken in arriving at the final state of strain, $\varepsilon_{ij}$. As it turns out, the second-order elastic constants are in fact, well-defined path-independent quantities which depend only upon the final state of strain.
由此产生的应力张量 $\sigma_{ij}$ 取决于最终应变状态的路径 $\varepsilon_{ij}$。事实证明,二阶弹性常数实际上是定义明确的与路径无关的量,只取决于最终的应变状态。
In a typical experiment, however, the sound speeds may be measured as a function of applied stress, $\sigma_{ij}$, not applied strain, $\varepsilon_{ij}$, and so the sound speeds, considered as a function of applied stress, depend upon the order in which those stresses are applied. If the deformation path can be parameterized by some known functions, $\{\varepsilon_{ij}(\xi)\}$ where $\xi$ is a convenient parameter, the relationship between sound speeds and applied stress can be derived.
然而,在典型的实验中,声速可能是作为外加应力($\sigma_{ij}$)而不是外加应变($\varepsilon_{ij}$)的函数来测量的,因此作为外加应力函数的声速取决于外加应力的顺序。如果变形路径可以用一些已知函数参数化,即 $\{\varepsilon_{ij}(\xi)\}$,(其中 $\xi$ 是一个为方便设定的参数),就可以得出声速与外加应力之间的关系。
For the special case of loose beads in which the system is hydrostatically compressed to its final pressure, $p$, the ema expressions for $K$ and $\mu$ are particularly simple. $K$ is unchanged from Eq. (7) and $\mu$ is changed by virtue of the transverse forces:
$$ K = \frac{C_{n}}{12\pi}[(1-\phi)Z]^{2/3}\left[\frac{6\pi p}{C_{n}}\right]^{1/3}, \tag{10}\label{eq10} $$ $$ \mu = \frac{C_{n} + \frac{3}{2}C_{t}}{20\pi}[(1-\phi)Z]^{2/3}\left[\frac{6\pi p}{C_{n}}\right]^{1/3}.\tag{11}\label{eq11} $$
We see that $K$ is predicted to be independent of $C_{t}$ and $\mu$ is predicted to be linearly dependent upon $C_{t}$, a point to which we return later.
对于松散球珠的特殊情况,即系统被静液压压缩至最终压力 $p$,$K$ 和 $\mu$ 的 ema 表达式特别简单。$K$ 与公式 (7) 一致,而 $\mu$ 则因横向力而改变:
$$ \begin{aligned} K &= \frac{C_{n}}{12\pi}[(1-\phi)Z]^{2/3}\left[\frac{6\pi p}{C_{n}}\right]^{1/3},\\ \mu &= \frac{C_{n} + \frac{3}{2}C_{t}}{20\pi}[(1-\phi)Z]^{2/3}\left[\frac{6\pi p}{C_{n}}\right]^{1/3}. \end{aligned} $$
The ema can be applied to any stress protocol, not just hydrostatic stress. In Fig. 3 we show the results of measurements of sound speeds on loose glass beads confined to a rigid cylinder. This is the so-called uniaxial strain test. The speeds are plotted as a function of applied stress, $\sigma_{zz}$. We show the predictions of the effective medium theory, in which certain reasonable assumptions about some of the parameters were made. (See Ref. [10] for details.) We see that the application of non-hydrostatic stress breaks the symmetry of the system, with the result that the speed of a longitudinal wave traveling along the direction of the applied stress increases more rapidly than that propagating perpendicular to it.
ema 可以应用于任何应力协议,而不仅仅是等静压力。图 3 显示了对约束在刚体圆柱中的松散玻璃珠的声速测量结果。这就是所谓的单轴应变测试。声速是外加应力 $\sigma_{zz}$ 的函数。我们展示了有效介质理论的预测结果,其中对某些参数做了合理的假设(详见参考文献 [10])。我们看到,非等静应力的施加打破了系统的对称性,结果是沿施加应力方向传播的纵波的速度比垂直于施加应力方向传播的纵波的速度增加得更快。
Additionally, a transverse wave propagating perpendicular to the direction of applied stress can have two inequivalent polarizations each of which is different than that of a transverse wave parallel to the direction of applied stress. The effective medium theory for the different sound speeds is in rough accord with the experimental data.
此外,垂直于外加应力方向传播的横波可以有两个不等效的极化,每个极化都不同于平行于外加应力方向的横波。不同声速的有效介质理论与实验数据基本一致。
Molecular dynamics simulations
With reasonable choices of the relevant parameters, the effective medium theories described above can give a good approximate description of the acoustic properties of granular media, as in Fig. 1, but there are problems, even for the simplest case of unconsolidated beads: (1) The effective medium theory predicts that the second order moduli vary with confining pressure as $p^{1/3}$, regardless of the values of coordination number, $Z$, and regardless of the values of $C_{n}$ or $C_{t}$. It is clear from Fig. 1 that the real data do not obey this power law.
在合理选择相关参数的情况下,上述有效介质理论可以很好地近似描述颗粒介质的声学特性,如图 1 所示,但即使对于最简单的未固结珠子情况也存在问题:(1)有效介质理论预测二阶模量随约束压力的变化为 $p^{1/3}$,与配位数 $Z$、$C_{n}$ 或 $C_{t}$ 的值无关。从图 1 中可以明显看出,实际数据并不服从这一幂律。
(2) Absent a molecular dynamics simulation, one does not know the appropriate value of the average coordination number, $Z$, to use in Eqs. (10) and (11). (3) The ratio $K/\mu$, or, equivalently $V_{p}/V_{s}$, is predicted from Eqs. (10) and (11) to be independent of pressure. Experimentally the ratio $K/\mu$ is indeed roughly constant but with a value which is intermediate between the two ema predictions, Eqs. (7) and (8) on the one hand, and Eqs. (10) and (11) on the other. Thus the implication is that $C_{t}$ (in Eq. (11)) is much smaller in real systems than expected from the Mindlin theory, Eq. (2), or that the ema is wrong.
(2) 在没有进行分子动力学模拟的情况下,我们不知道在公式 (10) 和 (11) 中使用的平均配位数 $Z$ 的适当值。(3) 根据公式 (10) 和 (11) 预测,比值 $K/\mu$,或等价于 $V_{p}/V_{s}$,与压力无关。实验结果表明,$K/\mu$ 的比值确实大致恒定,但其值介于两个 ema 预测值之间:一方面是公式 (7) 和 (8),另一方面是公式 (10) 和 (11)。因此,这意味着实际系统中的 $C_{t}$ (式 (11))比 Mindlin (式 (2)) 所预期的要小得多,或者说 ema 是错误的。
These facts have motivated us to undertake molecular dynamics simulations. In Fig. 4 we show the existing experimental data for $K$ and $\mu$ on loose glass beads along with predictions of the effective medium theory (Eqs. (10) and (11)). From the simulations we find that the numerical value of the average coordination number is $Z\approx 6$ (not $Z=9$ as in Fig. 1) for pressures less than $200\text{ MPa}$, so this is the value we use in Eqs. (10) and (11). We also show the results for our simulations.
这些事实促使我们进行分子动力学模拟。图 4 显示了松散玻璃珠上 $K$ 和 $\mu$ 的现有实验数据以及有效介质理论的预测值(公式 (10) 和 (11))。通过模拟我们发现,在压力小于 $200\text{ MPa}$ 时,平均配位数的数值为 $Z\approx 6$(而不是图 1 中的 $Z=9$),因此这就是我们在公式 (10) 和 (11) 中使用的数值。我们还展示了模拟结果。
Although there is scatter within and disagreement between the different data sets, we see immediately that the simulations, the effective medium theory, and the data are in reasonable agreement for the bulk modulus, $K$. The experimental data and the simulations are in reasonable agreement for $\mu$. The ema, however, signi"cantly over-predicts $\mu$. Our conclusions are that the assumption of the Hertz-Mindlin contact law, Eqs. (1) and (2), is not seriously in error, the ema is quite accurate in predicting $K$, and it is quite inaccurate in predicting $\mu$.
虽然不同数据集之间存在差异和分歧,但我们一眼就能看出,模拟、有效介质理论和数据在体积模量 $K$ 方面是合理一致的。对于 $\mu$ 而言,实验数据和模拟数据是合理一致的。然而,ema 对 $\mu$ 的预测明显过高。我们的结论是,Hertz-Mindlin 接触定律的假设(公式 (1) 和 (2))没有严重错误,ema 在预测 $K$ 时相当准确,而在预测 $\mu$ 时相当不准确。
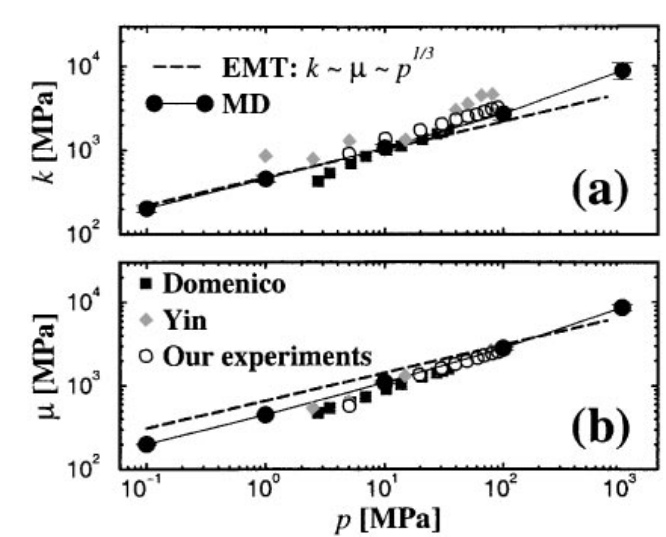
Pressure dependence of the elastic moduli from MD, experiments, and path dependent ema: (a) bulk modulus, and (b) shear modulus. The data are from Refs. [9,11,12].
从 MD、实验和路径依赖的 ema 得出的弹性模量的压强依赖性:(a) 体积模量,(b) 剪切模量。数据来自参考文献 [9,11,12]。
According to the ema, the transverse force, $f_{t}$, contributes only to the shear modulus and not to the bulk modulus. Thus, we are motivated to examine molecular dynamic simulations in which $C_{t}$ in Eq. (2) is replaced by $\alpha C_{t}$ where the dimensionless parameter $\alpha$ is varied from $0$ to $1$. The results for a confining pressure of $p=100\text{ kPa}$ are shown in Fig. 5, along with the predictions of Eqs. (10) and (11). The simulations confirm that $K$ is essentially independent of the strength of the transverse force. Astonishingly, the shear modulus is extremely sensitive in that it (nearly) vanishes as $\alpha\rightarrow 0$, in sharp contrast to the prediction of Eq. (11).
根据 ema,横向力 $f_{t}$ 只对剪切模量有贡献,而对体积模量没有贡献。因此,我们研究了分子动力学模拟,将公式 (2) 中的 $C_{t}$ 替换为 $\alpha C_{t}$,其中无量纲参数 $\alpha$ 变化范围是从 $0$ 到 $1$。图 5 显示了约束压力为 $p=100\text{ kPa}$ 时的结果,以及公式 (10) 和 (11) 的预测值。模拟结果证实 $K$ 基本上与横向力的强度无关。令人惊讶的是,剪切模量极其敏感,当 $\alpha\rightarrow 0$ 时,它(几乎)消失,这与公式 (11) 的预测形成了鲜明对比。
What is the most serious problem with the ema? We believe it to be the “affine assumption” we discussed earlier. Thus, we redo the numerical simulations by forcing each ball to translate according to Eq. (3) and not rotate at all. Finally, these simulations, which are also shown in Fig. 5 are indeed in agreement with the ema predictions, Eq. (11). What is evidently happening in the unconstrained simulations, and in the experiments, is that the beads in the immediate neighborhood of each grain move around relative to the central grain in such a way that if there are central forces only ($C_{t} = 0$), there is a nearly complete relaxation of the system to an applied shear. The system is a fluid, or nearly so.
ema 最严重的问题是什么?我们认为是我们之前讨论过的 “仿射假设”。因此,我们重新进行了数值模拟,强迫每个球根据公式 (3) 进行平移,而完全不旋转。最后,这些模拟结果也如图 5 所示,确实与公式 (11) 中的 ema 预测一致。在无约束模拟和实验中明显发生的情况是,每个颗粒附近的珠子相对于中心颗粒左右移动,如果只有对心力($C_{t} = 0$),系统对外加剪切力几乎完全弛豫。这个系统是一个流体,或者说几乎就是。
Conclusions
We have found that: (1) The Hertz-Mindlin contact theory is a good approximation to the actual grain-grain contact law in real glass bead systems subjected to a known stress. (2) The very simple effective medium approximation gives a reasonable, if approximate, description of the response of the system. (3) There is a big difference between systems in which the forces may be presumed to be conservative and path independent and those for which the forces are path dependent. In the former, a hyper-elastic theory of the elastic constants may be developed whereas in the latter the third-order (and higher-order) constants are undefinable. (4) The molecular dynamic simulations establish the validity of the effective medium theory for the bulk modulus and also establish that the ema for the shear modulus is in serious error. The problem lies with the inability of the ema to correctly treat the relaxation of the surrounding grains when a shear deformation is applied.
我们发现(1) Hertz-Mindlin 接触理论是实际玻璃珠系统在已知应力作用下颗粒-颗粒接触规律的良好近似。(2) 非常简单的有效介质近似对系统的响应进行了合理的描述,即使只是近似描述。(3) 在可以假定力是保守的、与路径无关的系统与那些力与路径有关的系统之间存在着很大的差异。在前者中,可以建立弹性常数的超弹性理论,而在后者中,三阶(和更高阶)常数是无法定义的。(4) 分子动力学模拟证明了有效介质理论对体积模量的有效性,同时也证明了剪切模量的 ema 存在严重错误。问题在于当施加剪切变形时,ema 无法正确处理周围颗粒的弛豫。

