Abstract
We have identified, according to the ratio of the wavelength to the grain size, two distinct types of pulsed ultrasound transmission through a dry bead packing under stress: one corresponds to coherent ballistic waves characterized by the effective medium description, the other to the waves scattered by the inhomogeneous stress field within the granular medium. Over long distances of transport, the multiply scattered waves exhibit a diffusive character. Also we investigate the dynamics of the granular medium during a compaction under cyclic loading-unloading.
Both the macroscopic deformation and the microscopic rearrangement have been measured, via an ultrasonic correlation technique using the multiple acoustic scattering very sensitive to the change of the system configuration. It is found that as the packing fraction increases, there is a continuous evolution of the system in response to external loading, from an irreversible behavior towards more elastic one.
我们根据波长与颗粒大小之比,确定了两种不同类型的脉冲超声波在应力作用下通过干燥小球堆积的传输方式:一种是以有效介质描述为特征的相干弹道波,另一种是颗粒介质内不均匀应力场散射的波。在长距离传输过程中,多重散射波表现出扩散特性。此外,我们还研究了颗粒介质在循环加载-卸载的压实过程中的动力学。
通过对系统构造变化非常敏感的多重声散射超声相关技术,测量了宏观变形和微观重排。研究发现,随着体积分数的增加,系统对外部载荷的反应会发生连续演化,从不可逆表现转变为更具弹性的行为。
Introduction
The study of granular media is of great current interest both scientifically and practically. In a static assembly of cohesionless grains, experimental observations (e.g., photoelastic visualization) and computer simulations have shown very inhomogeneous spatial distributions of contact forces between particles, organized along force chains which extend over a scale of order 5-10 grains diameters. These force chains, carrying most of the forces in the system, involve only a small fraction of the total number of grains and are only marginally stable (“fragile matter”).
Any external (thermal or mechanical) perturbation incompatible with the structure of the force chains or/and of sufficiently high amplitude, can lead to the plastic rearrangement of the system. Some new constitutive laws have been recently proposed to describe the static force transmission along the privileged force paths within granular systems and the instability of the force networks. In contrast to the conventional elastic description based on continuum mechanics, the equations governing the transmission of forces are hyperbolic instead elliptical, which lead to certain preferred directions as shown by experiments.
对颗粒介质的研究在科学和实践方面都具有重大意义。在无内聚力颗粒的静态聚集体系中,实验观察(如光-弹性可视化)和计算机模拟显示,颗粒间接触力的空间分布非常不均匀,这些接触力沿着力链分布,延伸范围约为 $5-10$ 个颗粒直径。这些力链承载了系统中的大部分力,但只涉及颗粒总数中的一小部分,而且只具有微弱的稳定性(“脆弱物质”)。
任何与力链结构不相容或/和振幅足够大的外部(热学或力学上的)扰动都会导致系统的塑性重排。最近有人提出了一些新的构成定律,用于描述粒状系统内沿特殊力路径的静态力传递以及力网络的不稳定性。与基于连续介质力学的传统弹性描述不同,这些力传递方程是双曲的,而不是椭圆的,这导致了实验所显示的某些优先方向。
Sound propagation in a disordered granular medium is of fundamental interest (multiple scattering). It also provides a very useful, and sometimes unique, probe of the internal structure such as force networks and the mechanical properties of real 3D granular packings, where the coherent photoelastic methods become impracticable.
In this paper, we investigate via ultrasound propagation, the dynamic force transmission at small amplitudes in glass bead packings under stress. Emphasis will be put on relevant length scales of observation for separating the different regimes of wave phenomena. Also the compaction of the granular packings under cyclic loading-unloading will be observed, in particular by measuring the correlation function of multiply scattered waves between successive runs.
在无序颗粒介质中的声音传播具有重要意义(多重散射)。在相干光-弹性方法不可行的情况下,它还提供了一种非常有用的、有时甚至是唯一的方法,来探测真实三维颗粒堆积的内部结构(如力网络和机械性能)。
在本文中,我们将通过超声波传播研究玻璃珠堆积在应力作用下的小振幅动态力传递。重点是观察关联长度的尺度,以区分不同的波现象。此外,还将观察颗粒堆积在循环加载-卸载过程中的压实情况,特别是通过测量连续运行之间多重散射波的关联函数。
EXPERIMENTAL TECHNIQUE
A schematic diagram of the experimental apparatus is shown in Fig. 1. Granular materials consist of random packings of mono- or poly-disperse glass beads. The sizes of the beads used in our experiments range from $400\mu\text{m}$ to several millimeters. They are contained in an aluminum cylinder of $30\text{ mm}$ inner diameter with the top and bottom surfaces made of close-fitting pistons. The beads are poured gently into the container being vibrated horizontally, in order to prepare dense packed granular materials. A volume fraction of solid phase is thus obtained to be about 0.63.
实验装置示意图如图 1 所示。颗粒材料由单分散或多分散玻璃珠的随机堆积组成。实验中使用的玻璃珠大小从 $400\mu\text{m}$ 到几毫米不等。它们被装在一个内径为 $30\text{ mm}$ 的铝制圆筒中,圆筒的上下表面由紧密贴合的活塞制成。将珠子轻轻倒入水平振动的容器中,以制备致密的颗粒材料。固体相的体积分数约为 $0.63$。
A normal load $P$ ranged from 0.03 to 3 MPa is applied to the upper piston using a jackscrew arrangement (œdometric test). At such load level, stress transmitted to the grains across the hertzian contact force is expected dominant compared with gravity and capillary effect.
Compressional and shear waves are excited, by applying input pulses of one or more cycles centered at $500\text{ kHz}$ onto the corresponding piezoelectric transducers. The vibration amplitude of the acoustic source is about 10 nm, measured in air by means of an optical interferometer. Two sizes of ultrasonic receiver are used: a large one, equal to that of the emitter (30 mm in diameter), and a small one (2 mm in diameter).
使用千斤顶螺钉布置(几何试验)对上活塞施加 $0.03$ 至 $3$ 兆帕的法向载荷 $P$。与重力和毛细管效应相比,在这样的负载水平下,通过 Hertz 接触力传递到颗粒的应力预计会占主导地位。
通过向相应的压电换能器 (压电陶瓷) 施加以 $500\text{ kHz}$ 为中心的一个或多个周期的输入脉冲,可激发压缩波和剪切波。声源的振幅约为 $10\text{ nm}$,这个数值可以在空气中通过光学干涉仪测量。实验中使用了两种尺寸的超声波接收器:一个与发射器大小相等的大接收器(直径 $30$ 毫米)和一个小接收器(直径 $2$ 毫米)。
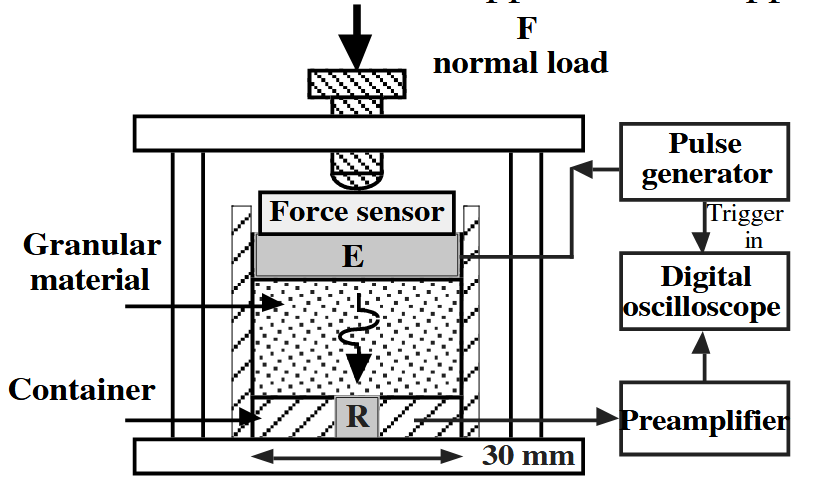
Schematic diagram of the vertical cross section of the apparatus. An aluminum cylinder contains the granular material. $E$ and $R$ correspond, respectively, to the ultrasonic emitter and receiver. A normal force is applied vertically upon the top piston of the container by using a jackscrew arrangement.
设备垂直横截面示意图。铝制圆筒中装有颗粒材料。$E$ 和 $R$ 分别对应超声波发射器和接收器。使用千斤顶螺钉装置对容器顶部活塞垂直施加法向力。
CHARACTERISTICS OF SOUND PROPAGATION
Typical ultrasonic transmission through the glass packing of bead size $d = 0.4-0.8\text{ mm}$ under an external load $P = 0.75\text{ MPa}$ (corresponding to 50 daN) is illustrated in Fig. 2a. It is excited by a one-cycle pulse of $2\mu\text{s}$ duration and detected by a longitudinal transducer of $30\text{ mm}$ in diameter placed at a distance $L \approx 11{ mm}$ away from the source.
The detected signal is basically composed of two parts, as observed in a previous work: a coherent ballistic pulse $E$ traveling through an “effective contact medium” with a velocity $V_{\text{eff}} ≈ 1000\text{ m/s}$, followed closely by speckle-like multiply scattered waves $S$ due to the inhomogeneous distribution of stress within the granular system.
图 2a 展示了在外部负载 $P = 0.75\text{ MPa}$(相当于 $50\text{ daN}$)条件下,超声波穿过尺寸为 $d = 0.4-0.8\text{ mm}$ 的玻璃球堆积的典型传输过程。它由一个持续时间为 $2\mu\text{s}$ 的 单周期 脉冲激发,并由一个直径为 $30\text{ mm}$ 的纵向传感器检测,该传感器放置在离源距离 $L \approx 11{ mm}$ 处。
检测到的信号基本上由两部分组成,正如之前的工作中所观察到的那样:一个相干的弹道脉冲 $E$ 以 $V_{\text{eff}} ≈ 1000\text{ m/s}$ 的速度穿过 “有效接触介质”, 紧随其后的是由于颗粒系统内应力分布不均而产生的斑纹状多散射波 $S$。
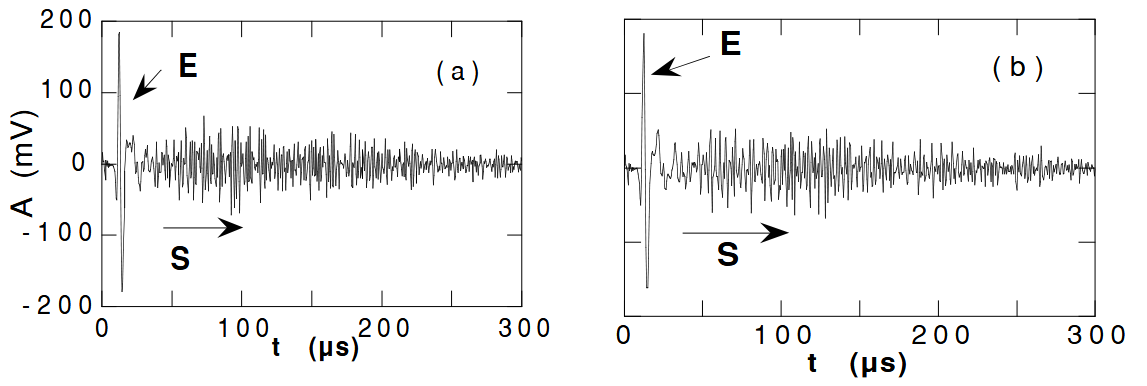
Transmitted ultrasonic signals through the bead packing of $d = 0.4 - 0.8\text{ mm}$ detected by a $30\text{-mm-diam}$ transducer obtained under the same applied stress $P = 0.75\text{ MPa}$ , first loading (a) and re-loading (b).
在相同的外加应力 $P = 0.75\text{ MPa}$ 下,首次加载(a)和重复加载(b)时,通过 $30\text{-mm-}$直径 传感器检测到的 $d = 0.4 - 0.8\text{ mm}$ 球珠堆积传输的超声波信号。
在数据或信号中,“斑”(speckle)通常指的是一种具有随机性质的、类似点状或斑点状的结构或图案。这种结构通常由许多微小的、不规则的或随机分布的元素组成,在光学、成像、声学或其他领域中都会出现。
结合给出的声学时域信号图应该能更好地体会到 speckle-like 所示的 “随机” 含义.
Indeed, by performing a separate spectral analysis, we find that $E$ carries a rather narrow band of low frequencies while $S$ has a broadband spectrum dominated by high frequency (Fig. 3a). As the bead size increases $(d = 1.5\text{ mm})$, the spectrum of $E$ shifts towards low frequencies while the spectrum of $S$ clearly exhibits a strong filtering out of high frequencies ($f > f_{c} \approx 500\text{ kHz}$) (Fig. 3b). This result suggests a frequency cut-off occurring when the wavelength $\lambda_{c} = V_{\text{eff}}/f_{c}$ is comparable to the bead size $d$.
事实上,通过进行单独的频谱分析,我们发现 $E$ 具有相当窄的低频带,而 $S$ 则具有以高频为主的宽带频谱(图 3a)。随着珠子尺寸的增大($d = 1.5\text{ mm}$),$E$ 的频谱转向低频,而 $S$ 的频谱则明显表现出强烈的低通特性($f > f_{c} \approx 500\text{ kHz}$)(图 3b)。这一结果表明,当波长 $\lambda_{c} = V_{\text{eff}}/f_{c}$ 与珠子大小 $d$ 相当时,会出现频率截断现象。
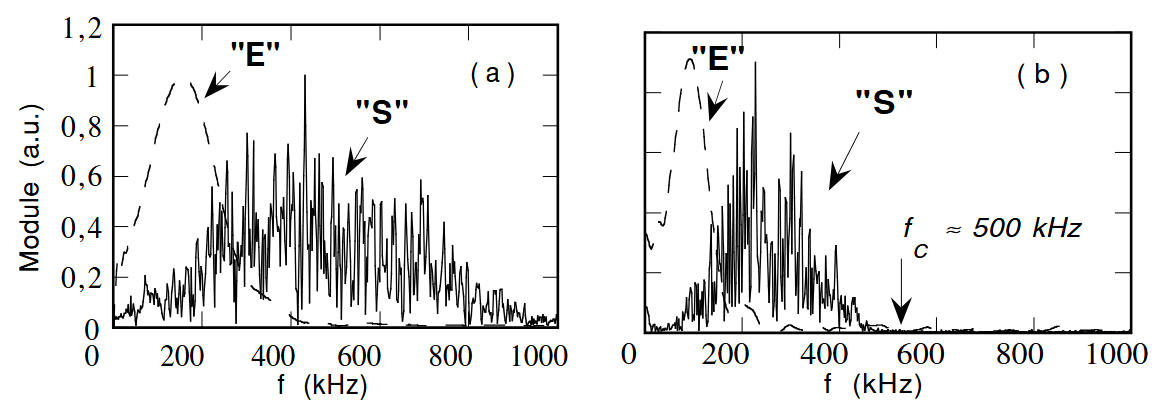
Spectra of the $E$ and $S$ signals windowed from the total temporal waveform in the bead packing of $d = 0.4-0.8\text{ mm}$ (a) and in that of $d = 1.5 \pm 0.15\text{ mm}$ (b)
从 $0.4-0.8\text{ mm}$ (a) 和 $0.15\text{ mm}$ (b) 的球珠堆积中的总时域波形中筛选出的 $E$ 和 $S$ 信号的频谱
如何从一个具体的时域信号中分解得到 $E$ 和 $S$, 并分别做频域分析呢?
Note also that the detected ultrasonic signals ($E$ and $S$) remain stable against repetitive averaging (~ 100) over the duration of an experimental run ($\leq 1\text{ min}$).
This excellent reproducibility of the signals shows that the ultrasound at small amplitudes (~ $10\text{ nm}$) used here, can propagate in the granular system under stress without producing any significant irreversible rearrangement. The characteristics of acoustic propagation in such a quasielastic medium can therefore be interpreted within the framework used to describe the vibrational properties of amorphous systems in terms of an inhomogeneous stress field.
还要注意的是,检测到的超声波信号($E$ 和 $S$)在实验进行期间($\leq 1\text{ min}$)(约 100 次)重复平均仍保持稳定。
信号的这种出色的复现性表明,这里使用的小振幅(~ $10\text{ nm}$)超声波可以在应力作用下的颗粒系统中传播,而不会产生任何明显的不可逆重排。因此,声波在这种准弹性介质中传播的特性可以在描述非均匀应力场下 无定形(非晶)系统 的振动特性这一框架内进行解释。
At the scale much larger than the bead size $d (= 0.4-0.8 \text{mm})$, the granular medium can thus be considered as homogeneous by a coarse-grained average. Since the coherent wave $E$ can only be self-averaging on a scale of order of its wavelength, this leads us to state that the correlation length of the stress filed is not large and cannot exceed a fraction of $\lambda_{\text{eff}}$, i.e. a few bead diameters - A result in qualitative agreement with the computer simulation and the photoelastic visualization.
在远大于珠子尺寸 $d (= 0.4-0.8 \text{mm})$ 的尺度上,颗粒介质可以通过 粗粒平均 被视为均质介质。由于相干波 $E$ 只能在其波长数量级的尺度上自平均,这就引导我们认为, 应力的关联长度并不大,不可能超过 $\lambda_{\text{eff}}$ 的分数,即几个球珠的直径–这一结果与计算机模拟和光弹性可视化在质量上是一致的。
A fundamental difference between $E$ and $S$ signals lies in their sensitivity to the change of the packing configuration. Fig. 2b illustrate temporal waveforms detected under the same external load $P = 0.75\text{ MPa}$ after performing an unloading-reloading cycle.
As clearly shown, $E$ exhibits a reversible behavior while $S$ is non-reproducible, i.e. configuration specific at the level of individual contacts. It is expected however that the global shape of $S$, which is determined by the statistical properties of the granular structure, shall be weakly altered by local irreversible events.
$E$ 和 $S$ 信号之间的一个基本区别在于它们对堆积结构变化的敏感性。图 2b 展示了在相同的外部负载 $P = 0.75\text{ MPa}$ 下,执行卸载-重载循环后检测到的时域波形。
如图所示,$E$ 表现出可逆行为,而 $S$ 则是不可复现的,即在单个接触点的水平上具有特定的构型。然而,由颗粒结构的统计特性决定的 $S$ 的全局形状预计将受到局部不可逆事件的微弱改变。
In order to make $S$ as a more quantitative probe to configuration variations, we shall study the transport characteristics of multiply scattered acoustic waves.
Fig. 4 presents the time dependence of the average intensity of the transmitted $S$ signal detected by a small detector of $2\text{ mm}$ in diameter. We used a ten-cycle pulse for excitation in order to have a well-defined frequency at $f = 500\text{ kHz}$, corresponding to a wavelength $\lambda\approx 2\text{ mm}$. This result was ensemble averaged over 50 different granular samples prepared in a similar way.
为了让 $S$ 更定量地探测构型变化,我们将研究多重散射声波的传输特性。
图 4 显示了直径为 $2\text{ mm}$ 的小型探测器检测到的传输 $S$ 信号平均强度的时间相关性。我们使用了一个 十周期 的脉冲进行激发,以便在 $f = 500\text{ kHz}$ 处有一个定义明确的频率,对应的波长为 $\lambda\approx 2\text{ mm}$。这一结果是以类似方法制备的 50 个不同颗粒样品的系综平均值。
Note that the time profile exhibits typical characteristics of a diffusive transport of strongly scattered sound observed in other random media. Using appropriate boundary conditions and resolving the diffusion equation, this will enable us to determine the diffusion coefficient and also the transport mean free path, being of the order of several bead sizes. More details about this study will be given elsewhere.
请注意,该时域曲线显示了在其他随机介质中观察到的强散射声扩散传播的典型特征。利用适当的边界条件并求解扩散方程,我们就能确定扩散系数和传输平均自由程,其大小相当于几个球珠(直径)的数量级。有关这项研究的更多详情将在其他地方提供。
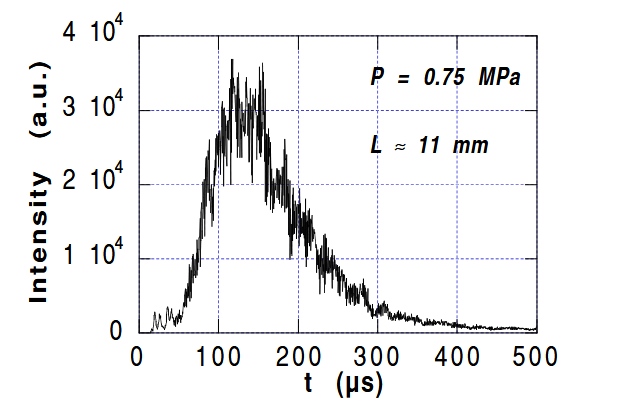
Time profile of the average intensity of multiple acoustic scattering transmitted the randomly close-packed glass beads $d = 0.4 - 0.8\text{ mm}$ for sample thickness $L\approx 11\text{ mm}$.
样品厚度为 $L\approx 11\text{ mm}$ 时,随机紧密堆积玻璃珠的多次声散射平均强度的时间曲线。
ACOUSTIC PROBING OF GRANULAR MATERIALS
Determination of elastic moduli 弹性模量的测定
Once the two distinct types of sound propagation in granular media are identified, we can unambiguously determine the compressional or shear wave velocities, $V_{P}$ and $V_{S}$ either by the time-of-flight method or by the phase spectrum analysis, if only the coherent $E$ signals are windowed from the total detected signal.
In the long-wavelength limit, the acoustic velocities are related to the bulk modulus $K$ and shear modulus $\mu$ of the granular material $V_{P} = [(K + 4/3\mu)/\rho]^{1/2}$ and $V_{S} = (\mu/\rho)^{1/2}$ where $\rho$ is the density of the material’s density.
一旦确定了声音在颗粒介质中传播的两种不同类型,我们就可以通过飞行时间法或相位频谱分析法,明确地确定压缩波或剪切波的速度 $V_{P}$ 和 $V_{S}$,前提是从总的检测信号中只选取相干的 $E$ 信号。
在长波极限下,声速与颗粒材料的体积模量 $K$ 和 剪切模量 $\mu$ 有关: $V_{P} = [(K + 4/3\mu)/\rho]^{1/2}$ 和 $V_{S} = (\mu/\rho)^{1/2}$ 其中 $\rho$ 是材料密度。
Coherent compressional and shear waves’ propagation in the bead packing of $d = 0.2-0.3\text{ mm}$, excited and detected by corresponding transducers, are shown in Fig. 5a. The measured shear wave velocity is given as a function of applied normal stress $P$ (Fig. 5b). The data behaves basically as a power law: $V_{S}\propto P^{1/4.8}$, similar to those observed for the compressional wave velocity.
图 5a 显示了由相应换能器激发和检测的相干压缩波和剪切波在(直径) $d = 0.2-0.3\text{ mm}$ 的球珠堆积中的传播情况。测得的剪切波速度是外加法向应力 $P$ 的函数(图 5b)。数据基本表现为幂律:$V_{S}\propto P^{1/4.8}$,与压缩波速度的观测结果类似。
The discrepancy between the experiment and the effective medium theory ($V_{S}\propto P^{1/6}$), based on the Hertz-Mindlin contact, is believed to be associated with the breakdown of the assumptions underlying the effective medium theory, i.e. the co-ordination number is pressure independent, which are not the case in granular media. On the other hand, the ratio of $K/\mu$ deduced from the experimental velocities ($V_{P} /V_{S}\approx 1.79$) differs significantly from the prediction of the effective medium theory.
实验与基于 Hertz-Mindlin 接触 的等效介质理论($V_{S}\propto P^{1/6}$)之间的差异, 被认为与等效介质理论的假设条件被破坏有关,即配位数与压力无关,而这在颗粒介质中并非如此。另一方面,从实验速度(拟合)推导出的 $K/\mu$ 比率($V_{P} /V_{S}\approx 1.79$)与等效介质理论的预测值相差很大。
One interpretation recently proposed points to the failure of the affine (well-bonded) approximation used in the effective medium theory for calculating the shear modulus $\mu$ of granular materials.
最近提出的一种解释指出,等效介质理论中用于计算颗粒材料剪切模量 $\mu$ 的仿射(良好结合)近似失效。
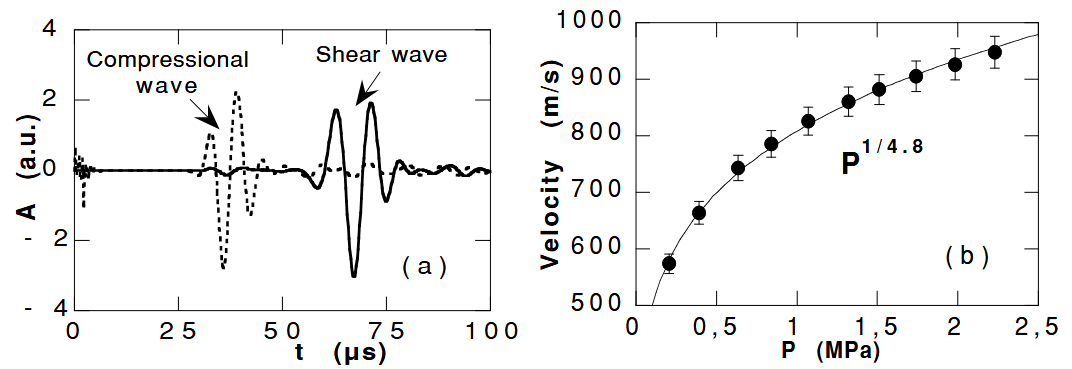
(a) Propagation of coherent effective waves in the glass bead packings of d = 0.2 - 0.3 mm under external stress P = 2.3 MPa. Solid and dashed curves correspond respectively to compressional and shear ballistic pulses. (b) Shear velocity VS (data points) measured as a function of the normal stress P. A power-law behavior is fitted approximately.
(a) 在外部压强 $P = 2.3$ 兆帕下,相干等效波在 $d = 0.2 - 0.3$ 毫米的玻璃珠堆积中传播。实线和虚线分别对应压缩和剪切弹道脉冲。(b) 作为法向应力 $P$ 的函数测量的剪切速度 VS(数据点)。
Compaction under cyclic loading-unloading
In the experiment a vertical column of $30\text{ mm}$ in diameter filled with polydisperse glass beads $d = 0.4 -0.8\text{ mm}$ to a initial height of $h_{0} = 10\text{ mm}$ was subjected to slowly repeated loading- unloading by the upper piston between $5\text{ daN}$ and $50\text{ daN}$ (Fig. 1). A displacement sensor monitors the resulting height (volume) change of the granular packing.
在实验中,一个直径为 $30\text{ mm}$ 的垂直柱中填充了多分散玻璃球 $d = 0.4 -0.8\text{ mm}$ ,初始高度为 $h_{0} = 10\text{ mm}$ ,上部活塞在 $5\text{ daN}$ 和 $50\text{ daN}$ 之间缓慢地重复加载-卸载(图 1)。位移传感器监测颗粒堆积的高度(体积)变化。
Fig. 6a illustrates the typical height variation of the granular packing measured with a force step of $5\text{ daN}$ for a few first cycles of loading-unloading. A few percent (~ $2%$) of the volume compaction ($\Delta h/h_{0}$), due to plastic rearrangement of grains, is observed after $n\sim 10$ cycles. Besides, $\Delta h(n)$ plot follows approximately a logarithmic law: $\Delta h/h_{0}\sim \ln(n)$, similar to those observed in the granular compaction subjected to vertical shakes with small amplitudes.
图 6a 展示了在加载-卸载的最初几个周期中,以 $5\text{daN}$ 的应力阶跃测量到的颗粒堆积的代表性高度变化。在 $n\sim 10$ 循环后,由于颗粒的塑性重排,可以观察到百分之几(~ $2%$)的体积压实($\Delta h/h_{0}$)。此外,$\Delta h(n)$ 图近似遵循对数规律:$\Delta h/h_{0}\sim \ln(n)$,这与受到小振幅垂直振动的颗粒压实中观察到的情况类似。
Now we present an original observation in which we make use of configuration-sensitive acoustic speckles $S$ to follow semi-quantitatively the irreversible rearrangement within the granular system during a macroscopic plastic deformation (compaction) produced by cyclic loading- unloading. To do so, we define a degree resemblance between two time signals $S_i(t)$ and $S_j(t)$, via their intercorrelation function $C_{i,j}(τ)$:
$$ \Gamma_{i,j}(\tau) = C_{i,j}(\tau)/[C_{i,i}(0)C_{j,j}(0)]^{1/2} $$
The value of $\Gamma_{i,j}(\tau=0)$ characterizes their resemblance and it is to be calculated for multiple acoustic scatterings transmitted through the granular material under successive cycles of loading- unloading ($n = i$ and $i + 1$). $\Gamma_{i, i+1} (0) = 1$ would correspond to an ideal solid having a pure elastic response to applied forces.
现在,我们提出一个新颖的观察方法,即利用构型敏感的声学峰 $S$, 半定量地跟踪颗粒系统在循环加载-卸载产生的宏观塑性变形(压实)过程中 内部 的不可逆重排。为此,我们通过两个时间信号 $S_i(t)$ 和 $S_j(t)$ 的相互关系函数 $C_{i,j}(τ)$ 来定义它们之间的相似度:
$$ \Gamma_{i,j}(\tau) = C_{i,j}(\tau)/[C_{i,i}(0)C_{j,j}(0)]^{1/2} $$
$\Gamma_{i,j}(\tau=0)$ 的值描述了它们的相似性,它是在连续的加载-卸载循环($n = i$ 和 $i+1$)下,通过颗粒材料传输的多次声散射计算得出的。$\Gamma_{i, i+1} (0) = 1$ 相当于理想固体对外力的纯弹性响应。
$\Gamma_{n, n+1}(0)$, deduced from the acoustic speckles between two successive cycles $n$ and $n+1$ (Fig. 6b), increases progressively as the system becomes more and more compacted. Since the acoustic speckle is configuration specific, this result simply indicates that greater is the packing fraction, more reversible and elastic behaves the granular system with respect to applied forces.
从两个连续周期 $n$ 和 $n+1$ 之间的声学峰(图 6b)推导出的 $\Gamma_{n,n+1}(0)$,随着(颗粒)系统变得越来越紧密而逐渐增加。由于声学峰是特定构型的,因此这一结果简单地表明,堆积分数越大,颗粒系统对外力的可逆性和弹性就越大。
This is intuitively reasonable because as the packing fraction increases the important arrangement of grains tends to disappear and the force network becomes more tangled, with many shorter intersecting chains as being photoelastically observed in 2D granular systems.
这在直觉上是合理的,因为随着堆积分数的增加,重要的晶粒排列趋于消失,力网络变得更加纠结,就像在二维颗粒系统中光弹性观察到的那样,有许多较短的相交链。
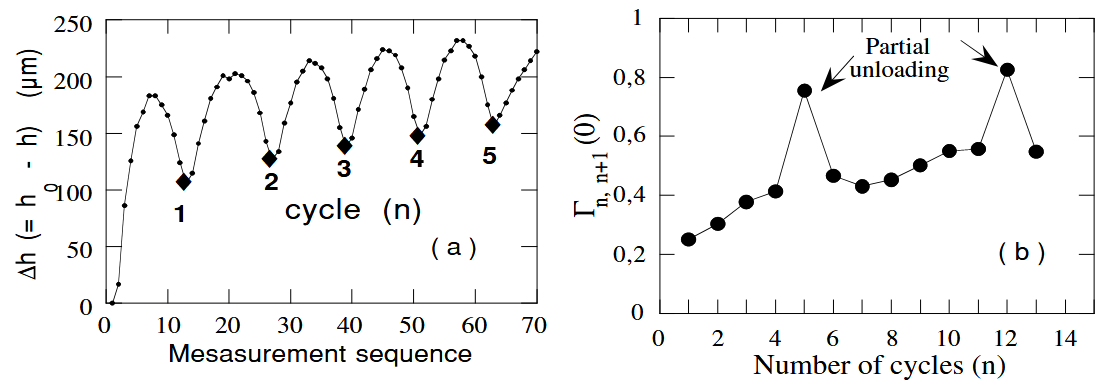
(a) Height (or volume) variation of the granular packing under cyclic loading- unloading. (b) Correlation of two S signals (multiply scattered waves) transmitted through the bead packing between two successive cyclic loading-unloading.
(a) 颗粒堆积在循环加载-卸载过程中的高度(或体积)变化。(b) 在两次连续的循环加载-卸载之间,通过颗粒堆积传输的两个 $S$ 信号(多重散射波)的相关性。
The two peaks observed in Fig. 6b are associated with partially unloading, i.e., unloading to $40\text{ daN}$ instead of $5\text{ daN}$, and then reloading to $50\text{ daN}$. For such a small perturbation, the granular system exhibits a quasielastic character. These results are reminiscent of the pastelike behavior observed in other media such as concentrated suspensions, foams, etc. More quantitative results are expected by using Diffusing Acoustic Wave Spectroscopy (DAWS) in development.
图 6b 中观察到的两个峰值与部分卸载有关,即卸载到 $40\text{ daN}$ 而非 $5\text{daN}$,然后重新负载到 $50\text{daN}$。对于如此小的扰动,颗粒系统表现出准弹性特征。这些结果让人想起在其他介质(如浓缩悬浮液、泡沫等)中观察到的糊状行为。通过使用正在开发中的扩散声波光谱法(DAWS),有望获得更多定量结果。
CONCLUSION
Ultrasound propagation in the glass bead packing reveals that for small amplitudes of force transmissions, the static granular system can be considered as a nonlinear quasielastic inhomogeneous medium, given external (œdometric) loading.
At scales of coherent waves much larger than the grain and the stress correlation lengths, the effective medium theory based on a coarse-grained average of contact mechanics gives a quite good description. When the wavelength shortened ultrasounds encounter successive scatterings caused by the inhomogeneous stress filed, which leads to the onset of a diffusive transport over long distance propagation.
超声波在玻璃珠堆积中的传播表明,在外部(œdometric)加载的情况下,对于较小的力传递振幅,静态颗粒系统可被视为非线性准弹性非均质介质。
在相干波的尺度(波长?)远大于晶粒和应力相关长度的情况下,基于接触力学粗粒平均值的有效介质理论给出了很好的描述。当波长缩短的超声波遇到由不均匀应力引起的连续散射时,就会在长距离传播过程中发生扩散传输。
At a scale comparable to the characteristic length of wave transport, of the order of the correlation length of stress, the acoustic force transmission is expected to be along certain preferred directions. We believe that the ultrasonic correlation technique (DAWS) used in the study of the granular compaction will facilitates the connection between the microscopic structure (configurational rearrangements) and the macroscopic behavior of granular materials in response to externally applied forces.
在与波传输特征长度(应力相关长度的数量级)相当的尺度上,预计声力传输将沿着某些优先方向进行。我们相信,用于研究颗粒压实的超声波相关技术(DAWS)将促进颗粒材料在外力作用下的微观结构(构型重排)与宏观行为之间的联系。

