X.jia
Abstract
Experimental observations of pulsed ultrasonic transmission through granular glass beads under oedometric loading are presented. We observe in the transmitted signals the coexistence of a coherent ballistic pulse traveling through an “effective contact medium” and a specklelike multiply scattered signal. The relative amplitudes of these signals strongly depend on the ratios of the bead size to the wavelength and to the detector size. Experimental data support recent descriptions of the inhomogeneous stress field within granular media.
本文介绍了在气压加载条件下脉冲超声波穿过颗粒状玻璃珠的实验观察结果。我们在传输信号中观察到,在 “有效接触介质” 中传播的相干弹道脉冲与斑点状多散射信号共存。这些信号的相对振幅在很大程度上取决于珠子大小与波长和探测器大小之比。实验数据支持最近对颗粒介质内不均匀应力场的描述。
Introduction
Granular media exhibit interesting and unusual properties, different from those of either solids or liquids. Photoelastic visualizations of $2$D and $3$D static confined granular systems under external stress have provided evidence of strong inhomogeneities in the distribution of contact forces between grains, giving rise to strong force chains extending over a scale much larger than the size of an individual grain. Characterizations of these stress distributions are of importance to the understanding of the structure and mechanical properties of granular media, in particular, in view of improving handling technologies.
颗粒介质显示出不同于固体或液体的有趣而不寻常的特性。对外部应力下的二维和三维静态密闭颗粒系统进行的光弹性可视化研究证明,颗粒之间的接触力分布具有很强的不均匀性,从而产生了比单个颗粒尺寸大得多的强力链。这些应力分布的特征对于了解颗粒介质的结构和机械特性非常重要,特别是在改进处理技术方面。
Owing to their efficient penetration inside elastic media, sound waves offer a very useful, and sometimes unique, technique for investigation of real (optically opaque or strongly light diffusing) 3D granular assemblies. The measurement of their velocity and attenuation can provide a sensitive probe of both the structure and mechanical properties of the material through which they propagate. The description of sound propagation in granular materials is thus a problem of fundamental interest. Recently, Liu and Nagel carried out a set of experiments involving sound propagation in a glass bead system under gravity.
由于声波在弹性介质中的高效穿透力,声波为研究真实的(光学不透明或强光扩散)三维颗粒集合体提供了一种非常有用,有时甚至是独一无二的技术。通过测量声波的速度和衰减,可以灵敏地探测声波传播所经过的材料的结构和机械特性。因此,描述声音在颗粒材料中的传播是一个具有根本意义的问题。最近,Liu 和 Nagel 进行了一组涉及重力作用下声音在玻璃珠系统中传播的实验。
In these experiments, sound pulses were generated via a loudspeaker and detected by a small microphone of size comparable with the grain diameter $d$. Typical responses in the time domain at low vibration amplitudes consisted of a sharp rising edge followed by a few strong spikes and a decaying tail. On the basis of the large difference between the time-of-flight velocity($\approx 300\text{m/s}$) and the group velocity($\approx 60\text{m/s}$) determined from the slope of the phase spectrum of the total detected signal, these authors claimed that there is an ambiguity about the determination of sound velocity in such a system.
Also, they found that sound propagation is very sensitive to changes in the packing configuration produced by thermal expansion of a single grain or by high amplitude vibrational excitation. They interpreted this as being due to sound propagating within the granular medium predominantly along strong force chains.
在这些实验中,声脉冲通过扬声器产生,并由一个与晶粒直径 $d$ 大小相当的小型传声器检测到。在低振动幅度下,时域中的典型响应包括一个急剧上升的边缘,随后是几个强烈的尖峰和一个衰减的尾部。根据飞行时间速度(约 $300\text{m/s}$)与根据总检测信号相位频谱斜率确定的群速度(约 $60\text{m/s}$)之间的巨大差异,这些作者声称在这种系统中声速的确定存在模糊性。
此外,他们还发现,声音传播对单粒热膨胀或高振幅振动激励所产生的堆积构造变化非常敏感。他们认为这是由于声音在颗粒介质中主要沿着强力链传播。
In soil mechanics and geophysics, however, the effective medium approach (a long wavelength description) has been commonly used to describe sound propagation in granular media, and the determination of the (compressional or shear) sound velocity does not seem problematic. This observation leads to a fundamental question: Is it possible to reconcile these two descriptions of sound propagation in a granular medium?
In this Letter, we address this question by presenting new results pertaining to the transmission of low amplitude ultrasonic pulses through noncohesive glass bead packings confined in a vessel under external load. Special emphasis will be put on the nature of sound propagation for different ratios of the wavelength to the size of the glass beads.
然而,在土壤力学和地球物理学中,有效介质方法(长波长描述)通常用于描述声音在颗粒介质中的传播,(压缩或剪切)声速的确定似乎不成问题。这一观察结果引出了一个基本问题:是否有可能调和这两种对声音在颗粒介质中传播的描述?
Experiments.
A schematic diagram of the experimental setup is shown in the inset of Fig. 1a. Our samples consist of random packings of glass beads, contained in a Plexiglas cylinder of height $35$ mm, inner diameter 30 mm, with the top and bottom surfaces made of close fitting pistons. The beads are poured into the container, being vibrated horizontally. The compactivity thus obtained is found to be of the order of $0.63$, and is reproducible, for a given bead sample, to within less than $1$%. Once the cell is filled, a normal load corresponding to apparent pressures $P$ ranging from $0.03$ to $3$ MPa is applied to the upper piston using a jackscrew arrangement, while the lower piston is held fixed (oedometric loading). At such load levels, the contribution of gravity to the stresses transmitted by the Hertzian contacts is negligible.
实验装置示意图见图 1a。我们的样品由随机包装的玻璃珠组成,装在一个有机玻璃圆筒中,圆筒高 $35$ 毫米,内径 $30$ 毫米,上下表面由紧密配合的活塞制成。将玻璃珠倒入容器中,并进行水平振动。由此获得的密实度约为 $0.63$,对于给定的珠子样品,其重现性小于 $1$%。样品池填满后,使用千斤顶螺杆装置向上部活塞施加与表观压强 $P$($0.03$ 至 $3$ 兆帕)相对应的法向载荷,同时下部活塞保持固定(气动载荷)。在这样的负载水平下,重力对赫兹触点传递应力的影响可以忽略不计。
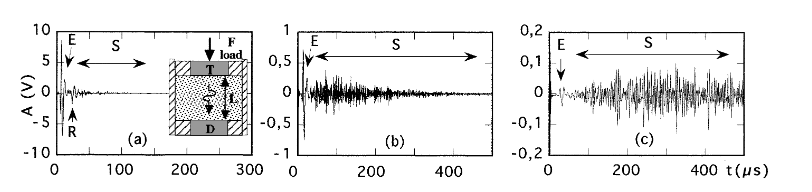
Ultrasonic signals measured by a 12-mm-diam transducer in glass bead packings of different sizes under external normal stress $P = 0.75\text{ MPa}$ at (a) $d = 0.2-0.3\text{ mm}$, (b) $d = 0.4-0.8\text{ mm}$, (c) $d = 1.5\pm 0.15\text{ mm}$. $E$ and $R$ correspond, respectively, to the coherent ballistic pulse and its echo reflected from the bottom and top surfaces. $S$ is associated with multiply scattered sound waves. The inset of (a) shows a schematic diagram of the apparatus: $T$ and $D$ are, respectively, the ultrasonic emitter and detector. Note the different time scale in (a).
在外部法向应力 $P = 0.75 \text{MPa}$ 的条件下,$12$ 毫米直径的传感器在不同尺寸的玻璃珠堆积中测得的超声波信号:(a) $d = 0.2-0.3$ 毫米,(b) $d = 0.4-0.8$ 毫米,(c) $d = 1.5 \pm 0.15$ 毫米。$E$ 和 $R$ 分别对应相干弹道脉冲及其从底部和顶部表面反射的回声。$S$ 与多重散射声波有关。(a) 的插图显示了仪器的示意图:$T$ 和 $D$ 分别是超声波发射器和探测器。请注意 (a) 中不同的时间尺度。
To optimize the ultrasonic excitation and detection, piezoelectric transducers, essentially sensitive to compressional vibrations along their axes, are put in direct contact with the glass beads at the top and bottom of the container (Fig. 1a). The acoustic source consists of a $12$ mm diameter uniformly vibrating transducer.
The excitation is realized by using one-cycle pulses of $2 \text{ms}$ duration with broadband spectrum ($20 \text{kHz}-1 \text{MHz}$) centered at $500 \text{kHz}$. The vibration amplitude of the source is measured to be $10 \text{nm}$ in air by means of an optical interferometer. As for the detector, centered on the axis of the source, two different transducers are used: a large one, of diameter $12$ mm equal to that of the emitter, and a small one, of diameter $2$ mm. The signal-to-noise ratio is improved by repetitive averaging of the detected signals using a digital oscilloscope and sent to a microcomputer for processing.
为了优化超声波激励和检测,将对沿其轴向的压缩振动非常敏感的压电传感器与容器顶部和底部的玻璃珠直接接触(图 1a)。声源由一个直径为 $12$ 毫米的均匀振动传感器组成。
激励是通过以 $500 \text{kHz}$ 为中心的宽带频谱($20 \text{kHz}-1 \text{MHz}$)、持续时间为 $2 \text{ms}$ 的单周期脉冲实现的。通过光学干涉仪测量,振源在空气中的振幅为 $10 \text{nm}$。至于以声源轴线为中心的探测器,则使用了两个不同的传感器:一个大的,直径为 $12$ 毫米,与发射器的直径相等;另一个小的,直径为 $2$ 毫米。通过使用数字示波器对检测到的信号进行重复平均,并将其发送到微型计算机进行处理,从而提高了信噪比。
Figure 1 illustrates ultrasonic signals transmitted through packings of beads of three different sizes (obtained from Centraver): (a) Polydisperse $d = 0.2-0.3$ mm; (b) polydisperse $d = 0.4-0.8$ mm; (c) $d = 1.5 \pm 0.15$ mm, under an external load $P = 0.75 \text{MPa}$.
They are detected with the large transducer, placed at the same reduced distance $L/d \approx 18$ away from the source. To ascertain that the ultrasound propagates from one grain to its neighbors only through their mutual contacts and not via air, we have checked that no ultrasonic signal is detected at vanishing external load. This test, together with the sound velocity measurements described below (Fig. 4), ensures that sound transmission through the interstitial fluid, i.e., Biot’s slow wave, is not involved in our experiments.
图 1 展示了在外加压强 $P = 0.75 \text{MPa}$ 的情况下,通过三种不同尺寸的珠子堆积传输的超声波信号(从 Centraver 获取):(a) 多分散 $d = 0.2-0.3$ mm;(b) 多分散 $d = 0.4-0.8$ mm;(c) $d = 1.5 \pm 0.15$ mm。
它们是用大型传感器检测到的,该传感器与声源的距离同样减小了 $L/d (约 18$)。为了确定超声波只通过晶粒间的相互接触而不是通过空气从一个晶粒传播到邻近晶粒,我们检查了在外部载荷消失时是否检测不到超声波信号。这一测试以及下文所述的声速测量(图 4)确保了我们的实验不涉及通过间隙流体传播的声音,即 Biot 慢波。
We first investigate the features common to all of the signals. Let us, for example, focus on the packing of intermediate size beads $(d = 0.4-0.8 \text{mm})$. As seen in Fig. 1b, the detected ultrasonic signal is basically composed of two parts:
(i) an early well-defined short pulse, which we label $E$,
(ii) closely followed by an irregular signal, $S$, which spreads over a time interval of hundreds of $\text{ms}$.
We determine a time of flight associated with the arrival of the $E$ pulse front, measured at an amplitude of $5$% of the peak-to-peak one, from which we obtain a velocity, $V_{\text{eff}} = 1070\pm 30\text{m/s}$. By performing a separate spectral analysis of $E$ and $S$, we find (Fig. 2) that $E$ carries a rather narrow band of low frequencies, while $S$ has a broadband strongly irregular high frequency spectrum.
我们首先研究所有信号的共同特征。例如,我们重点研究中等尺寸 $(d = 0.4-0.8 \text{mm})$ 珠子的堆积。如图 1b 所示,检测到的超声波信号基本上由两部分组成:
(i) 早期的清晰短脉冲,我们将其标记为 $E$;
(ii) 紧随其后的是不规则信号 $S$,它在数百毫秒的时间间隔内传播。
我们确定了与 $E$ 脉冲前沿到达相关的飞行时间,该时间的振幅为峰值的 $5$%,由此我们得到了一个速度 $V_{\text{eff}} = 1070\pm 30\text{m/s}$。通过对 $E$ 和 $S$ 进行单独的频谱分析,我们发现(图 2)$E$ 带有相当窄的低频带,而 $S$ 带有宽带、强烈不规则的高频频谱。
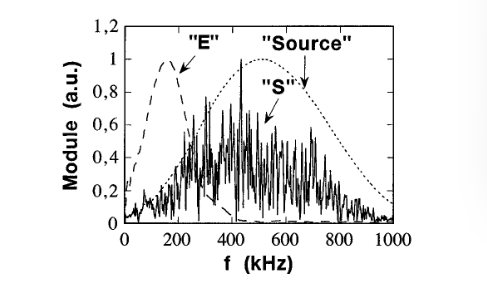
Spectra of the $E$ and $S$ signals windowed from the total temporal response. The spectrum of the injected pulse (source) is given for comparison.
从总时间响应中筛选出的 $E$ 和 $S$ 信号的频谱。注入脉冲(“Source”)的频谱可供比较。
On the other hand, we have investigated the effect of detector size. Figure 3a shows the signal detected by the small (2 mm wide) transducer on a packing of the same beads under the same load as in Fig. 1b. It is clearly seen that reducing the detector size leads to a considerable enhancement of the amplitude of S relative to E. Note that the irregular temporal fluctuations associated with S remain stable over the duration (typically ,1 min) of an experimental run. We have ascertained this by checking the reproducibility of the signal as well as its stability against the number (50 to 100) of repetitive averaging. That is, no “aging effect” is observed on this time scale. However, a weak evolution of the signals is identifiable on much longer time scales. A systematic study of this effect is in progress.
另一方面,我们还研究了探测器尺寸的影响。图 3a 显示了在与图 1b 相同的载荷下,小型($2$ 毫米宽)传感器在相同珠子堆积上检测到的信号。可以清楚地看到,减小探测器的尺寸会导致 $S$ 的振幅相对于 $E$ 有相当大的增强。请注意,与 $S$ 相关的不规则时间波动在实验运行的持续时间(通常为 $1$ 分钟)内保持稳定。我们通过检查信号的可重复性以及重复平均次数($50$ 至 $100$ 次)的稳定性来确定这一点。也就是说,在这个时间尺度上没有观察到 “老化效应"。不过,在更长的时间尺度上,可以发现信号的微弱变化。对这种效应的系统研究正在进行之中。
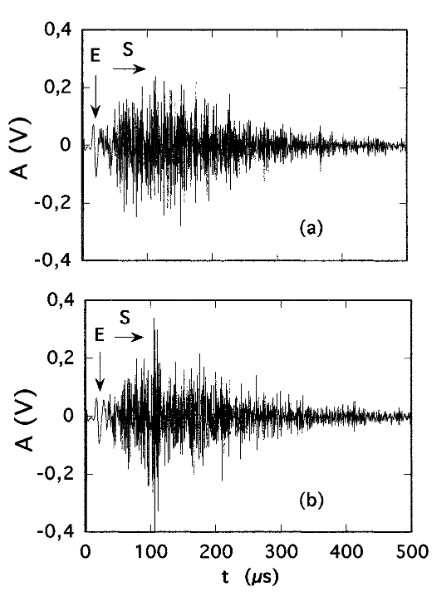
Ultrasonic signals through the same bead packing as Fig. 1b detected by a smaller transducer under the same normal stress $P = 0.75 \text{MPa}$: (a) First loading; (b) reloading.
在相同的法向应力 P = 0.75 兆帕(MPa)条件下,通过较小的传感器检测到的与图 1b 相同的微珠堆积的超声波信号:(a)首次加载;(b)再次加载。
A fundamental difference between $E$ and $S$ lies in their sensitivity to changes in packing configurations. This appears when comparing a first signal measured under a static load $P$ with that detected after performing a “loading cycle,” i.e., complete unloading, then reloading to the same $P$ level. As illustrated in Fig. 3, $S$ is highly nonreproducible, i.e., configuration sensitive.
However, $E$ exhibits a reversible behavior. More precisely, we characterize its degree of reproducibility by adjusting the reloading level to the value $P’$ which yields the best superposition between the two $E$ signals. We find that $\Delta P/P = (P’-P)/P$ is always no more than a few percent—for example, for the $0.4–0.8 \text{mm}$ bead packings at $P\approx 0.75 \text{MPa}$, $\Delta P/P\leq 4$%.
$E$ 和 $S$ 之间的根本区别在于它们对堆积结构变化的敏感性。将在静态负载 $P$ 下测量的第一个信号与执行 “加载循环”(即完全卸载,然后重新加载到相同的 $P$ 水平)后检测到的信号进行比较,就会发现这一点。如图 3 所示,$S$ 具有高度不可重复性,即对构型敏感。
然而,$E$ 表现出一种可逆的行为。更准确地说,我们通过将重负载水平调整到能产生两个 $E$ 信号之间最佳叠加的值 $P’$ 来描述其可复现性度。我们发现,$\Delta P/P = (P’-P)/P$ 总是不超过百分之几——例如,对于 $0.4-0.8 \text{mm}$ 的小珠堆积,在 $P\approx 0.75 \text{MPa}$ 时,$\Delta P/P\leq 4$%。
From these experimental results, we can reasonably infer that $E$ is a self-averaging signal, which thus probes sound propagation in an equivalent effective medium. This we confirm by determining its group velocity $V_{g}$ from the phase spectrum of $E$ alone, as windowed out of the total signal. This analysis is performed without deconvoluting the excitation pulse: Indeed, the known electric input pulse shape does not give any direct access to the excitation energy really injected through the transducer-granular medium inhomogeneous contact.
The frequency dependence of the phase is linear, indicating that $E$ corresponds to nondispersive wave propagation. Moreover, we find that, for all of our experiments, $V_{g}$ coincides with the time-of-flight velocity to within $20$% at most. That is, the velocity of the $E$ pulse unambiguously defines a sound velocity $V_{\text{eff}}$ in our granular medium.
This is confirmed by the agreement between the $P$ dependence of $V_{\text{eff}}$ , plotted in Fig. 4 for the $0.4–0.8 \text{mm}$ beads, with that found in previous works. Namely, $V_{\text{eff}}(P)$ follows a quasi power law, whose exponent slowly decreases from its low $P$ value, $\approx 1/4$, to the Mindlin-Hertz value, $1/6$, at high load. We can also define an effective acoustic wavelength associated with the $E$ pulse: $\lambda_{\text{eff}} = V_{\text{eff}}/\nu$(with $\nu$ the central frequency of $E$) of an order of several $\text{mm}$ in our experiments.
从这些实验结果中,我们可以合理地推断出 $E$ 是一个自平均信号,因此它探测的是声音在等效有效介质中的传播。我们通过从总信号中筛选出的 $E$ 的相位频谱单独确定其群速度 $V_{g}$,从而证实了这一点。这一分析是在没有对激励脉冲进行去卷积的情况下进行的:事实上,已知的电输入脉冲形状并不能直接获得通过传感器-颗粒介质非均质接触真正注入的激励能量。
相位的频率依赖性是线性的,这表明 $E$ 与非色散波传播相对应。此外,我们还发现,在所有实验中,$V_{g}$ 与飞行时间速度的重合度最多在 20% 以内。也就是说,$E$ 脉冲的速度毫不含糊地定义了颗粒介质中的声速 $V_{\text{eff}}$。
图 4 中绘制的 $V_{\text{eff}}$ 与 $0.4-0.8 \text{mm}$ 珠子的 $P$ 相关性与之前工作中发现的 $V_{\text{eff}}(P)$ 之间的一致性证实了这一点。也就是说,$V_{\text{eff}}(P)$ 遵循准幂律,其指数从低 $P$ 值($\approx 1/4$)缓慢下降到高负载时的 Mindlin-Hertz 值($1/6$)。我们还可以定义与 $E$ 脉冲相关的有效声波波长:$\lambda_{\text{eff}} = V_{\text{eff}}/\nu$(在我们的实验中,$\nu$ 是 $E$ 的中心频率),其量级为几 $\text{mm}$。
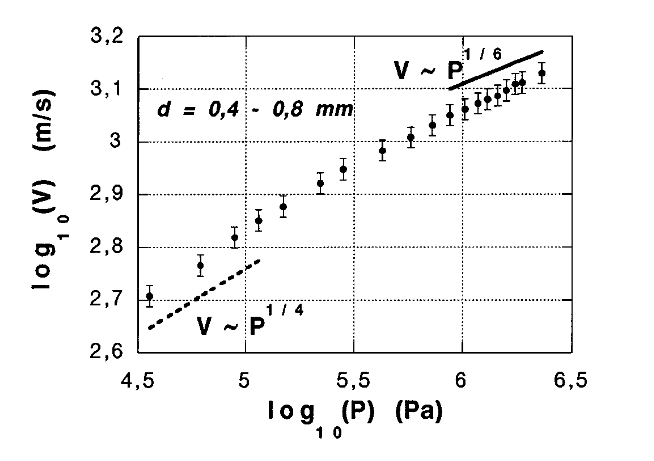
Sound velocity $V$ (data points) of the coherent $E$ wave in the bead packing, $d = 0.4-0.8 \text{mm}$ versus the applied stress $P$.
$d = 0.4-0.8 \text{mm}$ 珠状堆积中, 相干波 $E$ 的声速 $V$(数据点)与外加应力 $P$ 的关系。
Let us finally consider the effect of bead size. As illustrated in Fig. 1, the evolution of the signals transmitted through packings of beads of various sizes with the same reduced thickness $L/d$ exhibits systematic trends. As $d$ increases,
(i) the amplitude of the $E$ pulse decreases rapidly, with its spectrum shifting towards low frequencies, and
(ii) the amplitude of $S$ relative to $E$ increases; moreover, the spectrum of the $d = 1.5 \text{mm}$ sample clearly exhibits strong filtering out of high frequencies.
最后,让我们来看看小珠尺寸的影响。如图 1 所示,通过具有相同减薄厚度 $L/d$ 的不同尺寸珠子堆积传输的信号的变化呈现出系统性趋势。随着 $d$ 的增加
(i) $E$脉冲的振幅迅速减小,其频谱向低频移动,以及
(ii) $S$ 相对于 $E$ 的振幅增大;此外,$d = 1.5 \text{mm}$ 样品的频谱明显表现出对高频的强过滤。
Discussions.
For the frequencies used in our experiments, which lie much below the acoustic resonances $(\nu_{\text{res}}\approx V_{\text{glass}}/d)$ of individual glass beads, we can model the acoustic properties of the granular medium as those of a random network of point masses (the beads) connected by bonds—the frictional Hertz contacts between neighboring beads.
Mindlin has shown that, when such a contact is submitted to a static shear force $f_{\text{s}}$ lower than the static friction threshold ($f_{\text{s}} < \mu f_{\text{n}}$, with $f_{\text{n}}$ the normal load), its elastic shear and compressive stiffness are comparable, of order $d(PE^{* 2})^{1/3}$, with $E^{*}$, the elastic modulus of glass.
We know from experiments and simulations that, under static loading, the normal and shear loads of individual bead contacts exhibit a random distribution. Hence, the topological disorder of the granular medium induces space fluctuations of both density and local elastic stiffness.
我们实验中使用的频率远低于单个玻璃珠的声学共振频率 $(\nu_{\text{res}}\approx V_{\text{glass}}/d)$,因此我们可以将颗粒介质的声学特性建模为通过键(相邻玻璃珠之间的 Hertz 摩擦接触)连接的点质量(玻璃珠)随机网络的声学特性。
Mindlin 已经证明,当这种接触受到的静态剪切力 $f_{\text{s}}$ 低于静摩擦阈值($f_{\text{s}} < \mu f_{\text{n}}$,其中 $f_{\text{n}}$ 是法向载荷)时,其弹性剪切和压缩刚度是相当的,数量级为 $d(PE^{* 2})^{1/3}$,其中 $E^{*}$ 是玻璃的弹性模量。
我们从实验和模拟中得知,在静态载荷条件下,单个珠子接触点的法向载荷和剪切载荷呈现随机分布。因此,颗粒介质的拓扑结构紊乱会引起密度和局部弹性刚度的空间波动.
Such an elastic medium thus appears as closely analogous to an amorphous solid, and our observations can naturally be interpreted within the framework used to describe the vibrational properties of glassy solids in terms of an inhomogeneous stress field, e.g., irreversible changes of the packing configuration can be paralleled with irreversible flips of two-level states.
The excellent reproducibility of the signal from repeated pulses in a single run shows that, at the small vibration amplitudes used here, the triggering of such dissipative events by the sound pulse can be neglected.
因此,这种弹性介质与无定形固体非常相似,我们的观察结果可以很自然地在不均匀应力场描述玻璃固体振动特性的框架内进行解释,例如,堆积构型的不可逆变化可以与两级状态的不可逆翻转相提并论。
单次运行中重复脉冲产生的信号具有极佳的重现性,这表明在此处使用的小振动振幅下,声脉冲引发的这种耗散事件可以忽略不计。
We then propose the following qualitative picture. Our sample is contained in a long resonator with reflecting walls. If the sample was homogeneous, our wide acoustic emitter would excite essentially only the lowest mode of this wave guide. In the granular medium, such an injected pulse, as it propagates toward the detector, gets distorted by the disorder. We have seen that the $E$ signal propagates coherently with a well-defined sound velocity $V_{\text{eff}}$.
This allows us to define an effective wavelength associated with a frequency $\nu:\lambda_{\text{eff}} = V_{\text{eff}} / \nu$. The low frequency part of the pulse, for which $\lambda_{\text{eff}}\gg d$, experiences coherent but attenuated propagation in an average effective medium: This is precisely the $E$ signal.
Its coherence is proved by its reproducibility, together with the agreement between the time-of-flight $(V_{\text{eff}})$ and phase-analysis $(V_{g})$ eterminations of the coherent wave velocity. The scattering of this effective sound wave by the density and stiffness fluctuations results, on one hand, in its attenuation, which is clearly seen, e.g., on the reduced amplitude of the echo visible in Fig. 1a. They are, on the other hand, in their excitation of other modes of the resonator, responsible for the low frequency part of the $S$ signal.
随后,我们提出了以下定性描述。我们的样品收容在一个带反射壁的长形谐振器中。如果样品是均质的,我们的宽声波发射器基本上只能激发该波导的最低模式。而在粒状介质中,这种注入的脉冲在向探测器传播的过程中会受到无序的扭曲。我们已经看到,$E$ 信号以定义明确的声速 $V_{\text{eff}}$ 相干传播。
这样,我们就可以定义与频率 $\nu:\lambda_{\text{eff}} = V_{\text{eff}}$ 相关的有效波长 $\nu$。脉冲的低频部分($\lambda_{\text{eff}}\gg d$)在平均有效介质中进行相干但衰减的传播:这正是 $E$ 信号。
其相干性由其可重复性以及飞行时间速度 $(V_{\text{eff}})$ 与相干波速的相位分析 $(V_{g})$ 之间的一致性所证明。一方面,密度和刚度波动对这种有效声波的散射导致了声波衰减,这一点可以从图 1a 中可见的回声振幅减小等方面清楚地看到。另一方面,它们对谐振器其他模式的激励作用也导致了 $S$ 信号的低频部分。
However, most of the $S$ amplitude is due to higher frequency components, such that $\nu$~$V_{\text{eff}}/d$. In this frequency range, $\nu$ becomes comparable with a typical cutoff frequency of our discrete system. As illustrated in [12], the modes of the network develop strong space inhomogeneities, up to, finally, complete localization. In the intermediate frequency regime, propagation becomes quasidiffusive. This structure of the spectrum is responsible for the evolution of the signal with increasing bead size.
For $d = 0.2-0.3 \text{mm}$, most of the injection bandwidth corresponds to the long wavelength regime where the $E$ signal is dominant and scattering effects are small, in agreement with Rayleigh cross-section estimates. As $d$ increases, on one hand, the scattering cross section for given $\lambda$ increases as $(d/\lambda)^{4}$, hence the decrease of the amplitude of the unscattered $E$ coherent pulse. On the other hand, a larger fraction on the high $\nu$ end of the excitation band falls into the above-mentioned “stop band,” thus feeding the $S$ signal only up to below a cutoff frequency which decreases as $d$ increases.
然而,$S$ 振幅的大部分是由较高频率成分产生的,因此 $\nu$~$V_{\text{eff}}/d$。在这个频率范围内,$\nu$ 与我们离散系统的典型截止频率相当。正如文献[12]所述,网络的模会发展出很强的空间不均匀性,最终达到完全局域化。在中间频率区,传播变成了准扩散。这种频谱结构是信号随小珠尺寸增大而演变的原因。
对于 $d = 0.2-0.3 \text{mm}$,大部分注入带宽对应于长波段,在长波段中 $E$ 信号占主导地位,散射效应很小,这与 Rayleigh 截面估计值一致。随着 $d$ 的增大,一方面,给定 $\lambda$ 的散射截面会随着 $(d/\lambda)^{4}$ 的增大而增大,因此未散射的 $E$ 相干脉冲的振幅会减小。另一方面,在激发波段的高 $\nu$ 端,有较大部分落入上述 “停止波段”,因此只能在低于截止频率时馈入 $S$ 信号,而截止频率会随着 $d$ 的增加而降低。
$S$ thus appears as an acoustic speckle signal generated by the superposition of scattered waves—hence its delayed gradual rise, indicative of a quasidiffusive regime. As emphasized in [14], since acoustic detectors measure position integrated amplitudes, the larger the detector is, the more efficient is phase cancellation between the components of $S$. This accounts for the large relative amplification of $S$ that we observe with the small detector (Fig. 3).
This speckle nature of $S$ explains the nature of its variations under unloading-loading cycles. Indeed, as expected, configuration changes result in strong modifications of its detailed time structure. However, in agreement with our strong scattering picture, its global shape, which is determined by the gross statistical characteristics of the mode structure, is only weakly affected by irreversible events.
因此,$S$ 是由散射波叠加产生的声学散斑信号——因此,它的延迟渐升表明了一种准扩散机制。正如文献[14]所强调的,由于声学探测器测量的是位置积分振幅,因此探测器越大,$S$各分量之间的相位消除就越有效。这就是我们在使用小型探测器时观察到 $S$ 有较大相对放大的原因(图 3)。
$S$的这种斑点特性解释了其在卸载-加载循环下的变化性质。事实上,正如预期的那样,构型变化会导致其细致时间结构的剧烈变化。然而,与我们的强散射图景一致的是,由模式结构的总体统计特征决定的其总体形状只受到不可逆事件的微弱影响。
In summary, our experiments permit one to bridge between two apparently disconnected approaches to acoustic propagation in granular media, namely, the effective medium picture and the more recent one which stress mainly configuration sensitive effects. The fact that we have been able to observe, as far as we know, for the first time, the regime of coexistence of an attenuated coherent signal and its specklelike counterpart reconciles both points of view in terms of classical wave propagation in a random medium.
In particular, it is clear that the inconsistency found by Liu and Nagel between their time-of-flight and phase-analysis sound velocity determinations stems from the fact that they performed their phase analysis on the entire time signal, while such an analysis can only be meaningful once the $S$ signal has been windowed out. Note that their use of a detector of size comparable with bead diameter would have been quite unfavorable to the extraction of an $E$ signal, while, on the other hand, amplifying the sensitivity to local configuration changes.
总之,我们的实验使我们能够在颗粒介质中声波传播的两种看似互不关联的方法之间架起一座桥梁,这两种方法是有效介质理论和最近提出的主要强调构型敏感效应的理论。据我们所知,我们首次观测到了衰减相干信号与其斑点状对应信号共存的现象,这一事实从经典波在随机介质中传播的角度调和了两种观点。
特别是,Liu 和 Nagel 发现他们的飞行时间声速测定与相位分析声速测定之间存在不一致,这显然是由于他们对整个时间信号进行了相位分析,而这种分析只有在 $S$ 信号被窗口化后才有意义。需要注意的是,他们使用的探测器尺寸与珠子直径相当,这将非常不利于提取 $E$ 信号,而另一方面,却会放大对局部构型变化的敏感性。
We believe that our work points to the considerable interest in acoustic probing as a tool for studying of the mechanical properties of confined granular media. Clearly, before this can be undertaken, one should study in detail the sensitivity of the acoustic response to configurational variations.
Already at the present stage, an important semiquantitative conclusion emerges from our results: The $E$ signal is configuration insensitive. Since the coherent signal can only be self-averaging on a scale $\leq\lambda_{\text{eff}}$ , this leads us to state that the correlation length of the random density and, more importantly the stress field cannot exceed a fraction of $\lambda_{\text{eff}}$ , i.e., a few bead diameters—a result in qualitative agreement with the numerical results for a $2$D system and experimental data.
我们相信,我们的工作表明,人们对将声学探测作为一种研究密闭颗粒介质机械特性的工具相当感兴趣。显然,在此之前,我们应该详细研究声学响应对构型变化的敏感性。
在现阶段,我们的研究结果已经得出了一个重要的半定量结论:$E$ 信号对构型不敏感。由于相干信号只能在 $\leq\lambda_{\text{eff}}$ 的尺度上自平均,这使我们得出随机密度的相关长度,更重要的是应力场的关联长度不能超过 $\lambda_{\text{eff}}$ 的一部分,即几个珠子直径–这一结果与 $2$ D系统的数值结果和实验数据在性质上是一致的。

