Abstract
We measure the consequences of elastic heterogeneities in confined granular layers using long-wavelength sound velocity determination. By progressively decreasing the coarsegraining length $\omega$, which is determined here by the sample size $L$, we measure the standard deviation of the longitudinal sound velocity $\delta V_{L}$ and the packing density $\phi$, normalized by their ensemble-averaged values.
We find that the relative fluctuations in $V_{L}$ and $\phi$ increase when $\omega$ is decreased. Importantly, we observe that decreasing the confining pressure $P$ or using nonspherical particles leads to an important increase of the fluctuations in $\delta V_{L}/\bar{V}_{L}$.
我们利用长波声速测定法测量了凝结颗粒层中弹性异质性的后果。通过逐步减小粗粒化长度 $\omega$(在此由样本大小 $L$ 决定),我们测量了纵波声速 $\delta V_{L}$ 和堆积密度 $\phi$ 的标准偏差,并以它们的系综平均值归一化。
我们发现,当 $\omega$ 减小时,$V_{L}$ 和 $\phi$ 的相对波动会增大。重要的是,我们观察到,降低约束压力 $P$ 或使用非球形粒子会导致 $\delta V_{L}/\bar{V}_{L}$ 的波动显著增加。
$V_{L}$ 里的 $L$ 就是指的 longitudinal, 即压缩波的速度.
We conduct simulations of sound propagation in 2D hexagonal packings with contact-stiffness disorder to mimic the inhomogeneous contact networks. The sound velocity fluctuations of coherent longitudinal waves increase either with decreasing the sample size or with increasing the elastic disorder related to confining pressure, in consistency with the experiments.
Our experimental observations thus support the scenario of a pressure-dependent mesoscopic length $\xi\sim 10d$ (at $P\sim 200\text{ kPa}$), below which the continuum elasticity breaks down, likely due to the large spatial fluctuation of the shear modulus $\delta G/\bar{G}\sim 5\delta V_{L}/\bar{V}_{L} > 20$%.
我们模拟了声音在具有接触刚度无序的二维六方堆积中的传播,以模拟非均匀接触网络。相干纵波的声速波动随着样品尺寸的减小或与约束压力相关的弹性无序度的增加而增大,这与实验结果一致。
因此,我们的实验观察结果支持压力依赖性的介观长度 $\xi\sim 10d$(在 $P\sim 200\text{ kPa}$ 时)的设想,在此以下连续弹性会崩溃,这可能是由于剪切模量的空间波动 $\delta G/\bar{G}\sim 5\delta V_{L}/\bar{V}_{L}> 20$% 较大所致。
Introduction
Granular materials are dense collections of macroscopic constituent particles that play an important role in industrial and geophysical processes. These particles interact via repulsive contact forces forming complex and heterogeneous contact force networks. The mechanic behavior of granular materials is set by their force networks. To obtain its mechanical parameters on the macroscopic scale, a granular material can be treated as a continuous medium via the coarse-graining procedure.
颗粒材料是由宏观成分颗粒组成的致密集合体,在工业和地球物理过程中发挥着重要作用。这些颗粒通过排斥接触力相互作用,形成复杂的异质接触力网络。颗粒材料的力学行为由其力网络决定。为了获得宏观尺度上的力学参数,可以通过粗粒化处理视颗粒材料为连续介质。
The simplest model, namely, the effective medium theory (EMT) makes use of the affine approximation of deformation to derive the bulk $K$ (~ $Zk$) and shear moduli $G$ (~ $Zk$) from micromechanical parameters such as the contact stiffness $k\sim P^{1/3}$ (for the Hertzian contact) and the coordination number $Z$. These elastic properties can be related to the long-wavelength longitudinal (or compressional) and transverse (or shear) wave velocities by $V_{L} = ((K + 4/3G)/\rho)^{1/2}$ and $V_{T} = (G/\rho)1/2$ with $\rho$ the effective mass density of the granular packings.
最简单的模型,即等效介质理论 (EMT),利用变式的仿射近似,从微观力学参数,如接触刚度 $k\sim P^{1/3}$(赫兹接触)和配位数 $Z$ 推导出体积弹性模量 $K$ (~ $Zk$)和剪切模量 $G$ (~ $Zk$)。这些弹性特性可通过 $V_{L} = ((K + 4/3G)/\rho)^{1/2}$ 和 $V_{T} = (G/\rho)1/2$ 与长波纵向(或压缩)和横向(或剪切)波速关联,其中 $\rho$ 是颗粒堆积的等效质量密度。
Numerous studies have shown that the effective medium description breaks down in disordered granular packings especially near unjamming due to the important non-affine deformation. Specifically, the local deformation cannot follow the global deformation without the particle rearrangement and the shear modulus is particularly overestimated by the EMT.
Numerical simulations in frictionless sphere packings reveal that the peculiar scaling of the shear modulus follows $G\sim \Delta Z_{\text{iso}}k$, while the scaling of the bulk modulus remains similar as above $K\sim k$. Here $\Delta Z_{\text{iso}}\sim Z − Z_{\text{iso}}\sim P^{1/3}$ is the distance of the coordination number to the isostatic jamming point where the rigidity of the granular packing vanishes.
大量研究表明,有效介质描述在无序颗粒堆积中会出现问题,尤其是在接近解堵塞时,因为存在重要的非仿射变换。具体来说,在没有颗粒重排的情况下,局部变形无法跟随全局变形,而且 EMT 特别高估了剪切模量。
在无摩擦球堆积中进行的数值模拟显示,剪切模量的特殊缩放关系为 $G\sim \Delta Z_{\text{iso}}k$,而体积模量的缩放关系与上面的 $K\sim k$ 类似。这里 $\Delta Z_{\text{iso}}\sim Z - Z_{\text{iso}}\sim P^{1/3}$ 是配位数到等静堵塞点的差距,等静堵塞点是指颗粒堆积的刚度消失。
Moreover, the investigation of vibrational properties in the linear regime also reveals anomalous crossover behavior at low frequency $\omega = \omega^{*}$, beyond which the material exhibits an excess of low-frequency modes (i.e., boson peak). At the jamming point, $\omega^{*}\propto\Delta Z_{\text{iso}}$ vanishes and the material no longer exhibits the Debye-like behavior observed for an ordinary continuum medium.
此外,对线性机制中振动特性的研究还揭示了低频 $\omega = \omega^{*}$ 处的异常交叉行为,超过这个频率,材料就会表现出过量的低频模式(即玻色子峰)。在堵塞点,$\omega^{*}\propto\Delta Z_{\text{iso}}$ 消失了,材料不再表现出普通连续介质的类 Debye 行为。
In frictional sphere packings, the peculiar scaling behaviors of the elastic moduli $K$, $G$ and the characteristic frequency $\omega^{*}$ appears to remain valid; the crucial difference with the frictionless packings is that both the packing density $\phi$ and the contact (coordination) number $Z = Z_{c}$ at the jamming point $P = 0$ are not unique and both depend on the friction coefficient and on the packing history (here $Z_{c} > Z_{\text{iso}}$ is the critical coordination number; one has $Z_{c} = Z_{\text{iso}}$ for frictionless packings).
在有摩擦球堆积中,弹性模量 $K$、$G$ 和特征频率 $\omega^{*}$ 的奇特缩放行为似乎仍然有效;与无摩擦堆积的关键区别在于,堆积密度 $\phi$ 和堵塞点 $P = 0$ 处的接触(配位)数 $Z = Z_{c}$ 都不是唯一的,它们都取决于摩擦系数和堆积历史(这里的 $Z_{c}> Z_{\text{iso}}$ 是临界配位数;对于无摩擦堆积,有 $Z_{c} = Z_{\text{iso}}$)。
More precisely, it was shown that $G$ and $\omega^{*}$ still scale linearly with the distance to isostaticity $\Delta Z_{\text{iso}}$, but they no longer scale with the distance to jamming $\Delta Z_{c} = Z − Z_{c}\sim P^{1/3}$. This difference was also observed in experiments with surface acoustic waves in granular packings near the jamming point at $P\sim 0$.
更确切地说,研究表明 $G$ 和 $\omega^{*}$ 仍然与等静压距离 $\Delta Z_{\text{iso}}$ 成线性比例,但它们不再与堵塞距离 $\Delta Z_{c} = Z - Z_{c}\sim P^{1/3}$ 成比例。在颗粒堆积中的表面声波实验(接近 $P\sim 0$ 的堵塞点)中也观察到了这种差异。
Furthermore, the vanishing of a characteristic frequency $\omega^{*}$ tied to the anomalous low-frequency behavior indicates that the unjamming transition is accompanied by diverging length scales.
In frictionless packings, one of these length scales $l^{*}\sim 1/\Delta Z_{\text{iso}}$ proposed by Wyart et al. corresponds to the smallest size of a blob without it being floppy, i.e., the onset of rigidity; it may be related to $\omega^{*}$ by the longitudinal sound velocity $l^{*}\sim l_{L}\sim V_{L}/\omega^{*}\sim 1/\Delta Z_{\text{iso}}$. Another diverging length scale can be defined by the transverse sound velocity $l_{c}\sim l_{T}\sim V_{T}/\omega^{*}\sim 1/(\Delta Z_{\text{iso}})^{1/2}$.
此外,与反常低频行为相关的特征频率 $\omega^{*}$ 的消失表明,解堵塞转换伴随着长度尺度的发散。
在无摩擦堆积中,Wyart 等人提出的其中一个长度尺度 $l^{*∗*}\sim 1/\Delta Z_{\text{iso}}$ 对应于没有松动的圆球的最小尺寸,即, 它可以通过纵波声速 $l^{*}\sim l_{L}\sim V_{L}/\omega^{*}\sim 1/\Delta Z_{\text{iso}}$ 与 $\omega^{*}$ 相关。另一个发散长度尺度可以用横波声速 $l_{c}\sim l_{T}\sim V_{T}/\omega^{*}\sim 1/(\Delta Z_{\text{iso}})^{1/2}$ 来定义。
Recent numerical simulations showed that these length scales are on the order of a few particle diameter, which correspond likely to the force chains evidenced by the photoelastic visualization. They characterize the length over which the force networks in a given granular packing (or realization) look disordered or fluctuating after excitation by a zero-frequency point source or after an imposed global shear.
The lower is the pressure (and the smaller $\Delta Z_{\text{iso}}$), the larger are $l^{*}$ and $l_{c}$, even though the precise role of $l^{*}$ and $l_{c}$ remains debated. On the other hand, there exist extensive studies on amorphous solids and granular media addressing the question if a continuum elasticity can describe the response to an external forcing.
最近的数值模拟显示,这些长度尺度在几个颗粒直径的数量级上,很可能与光弹性可视化所显示的力链相对应。它们表征了特定颗粒堆积(或实现)中的力网络在受到零频点源激励或施加全局剪切后看起来无序或涨落的长度。
压力越低($\Delta Z_{\text{iso}}$ 越小),$l^{*}$ 和 $l_{c}$ 就越大,尽管 $l^{*}$ 和 $l_{c}$ 的确切作用仍存在争议。另一方面,关于无定形固体和颗粒介质的大量研究探讨了连续弹性是否能描述对外部作用力的响应这一问题。
Goldenberg and Goldhirsch have shown that linear elasticity is only valid for a sufficiently large coarse-graining length $\omega$, which should be larger than the mesoscopic length scale $\xi$ on the order of ten particle diameters. The $\xi$ describes the extent of local heterogeneities and it can be assessed by measuring the local elastic moduli as a function of the coarse-graining scale $\omega$ and monitoring the convergence to the macroscopic moduli (obtained by an additional ensemble-average over similarly prepared packings).
Goldenberg 和 Goldhirsch 已经证明,线性弹性只适用于足够大的粗粒度长度 $\omega$,它应该大于介观长度尺度 $\xi$,大约为 $10$ 个颗粒直径。$\xi$ 描述了局部异质性的程度,它可以通过测量局部弹性模量与粗粒度尺度 $\xi$ 的函数关系来评估,并监测与宏观模量的收敛情况(通过对类似制备的堆积进行额外的系综平均来获得)。
Continuum elasticity breaks down below the mesoscopic length scale $\xi$ as the deformation field of a given configuration (single realization) looks like a distorted floppy mode due to nonaffine displacements, resulting in a strong spatial fluctuation in the shear modulus. The question remains to know what controls this length scale. Ellenbroek et al. studied numerically the response of a 2D frictionless sphere packing to a global quasi-static shear deformation and they suggested that the mesoscopic length scale $\xi$ is proportional to the divergent length $l^{*}$. To our knowledge, there are few direct experimental investigations of these length scales particularly in the interior of optically opaque 3D frictional granular materials.
连续弹性在介观长度尺度 $\xi$ 以下就会崩溃,因为给定构型(单一实现)的形变场由于非仿射位移而看起来像一个扭曲的软模,从而导致剪切模量的强烈空间波动。问题仍然是如何控制这一长度尺度。Ellenbroek 等人用数值方法研究了二维无摩擦球堆积对全局准静态剪切变形的响应,他们认为介观长度尺度 $\xi$ 与发散长度 $l^{*}$ 成正比。据我们所知,关于这些长度尺度的直接实验研究很少,尤其是在光学不透明的三维 有摩擦 颗粒材料内部。
In this work we investigate the elastic heterogeneities in granular packings under compression using dynamic acoustic experiments. Measurements of the longitudinal sound velocity $V_{L}$ allow inferring the information on bulk and shear moduli. In the low-frequency or long- wavelength limit, considered here, the coarse-graining length $\omega$ is comparable to the wavelength $\lambda_{L}$ and larger than the mesoscopic scale $\xi$ and therefore the granular packings behave as a continuum medium on the macroscopic length scale approximately $L \geq \lambda_{L}$. This continuum description can be further improved by spatial averaging (similar to an ensemble average) using a largesize acoustic source and detector which partly cancel out the short-wavelength wave scattering (or fluctuation).
在这项工作中,我们利用动态声学实验研究了压缩条件下颗粒堆积的弹性异质性。通过测量纵波声速 $V_{L}$ 可以推断出体积模量和剪切模量的信息。在这里考虑的低频或长波极限中,粗粒化长度 $\omega$ 与波长 $\lambda_{L}$ 相当,大于介观尺度 $\xi$,因此颗粒堆积在宏观长度尺度上表现为近似于 $L \geq \lambda_{L}$ 的连续介质。这种连续介质描述可以通过使用大尺寸声源和探测器进行空间平均(类似于系综平均)来进一步改进,从而部分抵消短波长波散射(或涨落)。
To access the local heterogeneities below the scale $\xi$, which is smaller than $\lambda_{L}$, we monitor experimentally the relative standard deviations (fluctuations) of the sound velocity and of the packing density $\phi$. To do this, we determine for each sample thickness $L$ the $V_{L}$ and $\phi$ in 20 different samples (or realizations) and then normalize the standard deviation by its mean value. We vary $L$ from several tens of particles up to only a few particle diameters and repeat the experiments for different $P$ . We find that for $V_{L}$ the coarse-graining length is no longer determined by the wavelength but instead by the sample thickness.
为了获取小于 $\lambda_{L}$ 的尺度 $\xi$ 以下的局部异质性,我们通过实验监测声速和堆积密度 $\phi$ 的相对标准偏差(波动)。为此,我们为每个样本厚度 $L$ 确定 $20$ 个不同样本(或实现)中的 $V_{L}$ 和 $\phi$,然后用其平均值对标准偏差进行归一化处理。我们将 $L$ 的变化范围从几十个颗粒到只有几个颗粒直径,并对不同的 $P$ 重复实验。我们发现,对于 $V_{L}$,粗粒化长度不再由波长决定,而是由样品厚度决定。
We demonstrate that the fluctuation in $V_{L}$ is clearly pressure-dependent while the fluctuation in $\phi$ is not. By performing numerical simulations of sound propagation in 2D hexagonal packings with random contact stiffness between particles, we show that the fluctuation in the longitudinal sound velocity increases with increasing disorder and that it becomes predominant in thin samples. The consistence between measurement and simulation will be discussed.
我们证明了 $V_{L}$ 的波动明显与压力有关,而 $\phi$ 的波动则与压力无关。通过对颗粒间具有随机接触刚度的二维六方堆积中的声传播进行数值模拟,我们发现纵向声速的波动随着无序度的增加而增大,而且在薄样品中这种波动变得非常显著。我们将讨论测量与模拟之间的一致性。
Experiments
We studied the influence of the sample size on the applicability of an continuum elasticity by investigating the sound velocity and solid volume fraction (i.e., the packing density) for 7 different sample thicknesses $L$ at 3 different confining pressures $P$ . For each sample thickness, we performed 20 independent experiments from which we determined, after assembly averaging, the mean sound velocity $\bar{V}_{L}$ and mean solid volume fraction $\bar{\phi}$ as well as their standard deviations $\delta V_{L}$ and $\delta\phi$. These values were then used to calculate the relative fluctuations $C_{V_{L}} = \delta V_{L}/\bar{V}_{L}$ and $C_{\phi} = \delta\phi/\bar{\phi}$ as a function of the sample size.
我们通过研究 $7$ 种不同厚度 $L$ 的样品在 $3$ 种不同约束压力 $P$ 下的声速和固体体积分数(即堆积密度),研究了样品尺寸对连续弹性适用性的影响。对于每种厚度的样品,我们都进行了 $20$ 次独立实验,经过系综平均后,我们确定了平均声速 $\bar{V}_{L}$ 和平均固体体积分数 $\bar{\phi}$ 以及它们的标准差 $\delta V_{L}$ 和 $\delta\phi$ 。然后使用这些值计算相对波动 $C_{V_{L}} = \delta V_{L}/\bar{V}_{L}$ 和 $C_{\phi} = \delta\phi/\bar{\phi}$ 作为样本大小的函数。
Set-up and procedure
Our acoustic measurements were performed on a granular medium contained in a metal cylindrical cell with a diameter of $60\text{ mm}$ and of variable height $H$ (fig. 1). The granular medium consists of polydisperse glass beads or sand particles with mean diameter $d = 1.5$ and $1.8\text{ mm}$, respectively. The sample thickness is defined as the number of granular layers $L = H/d$. Broadband piezoelectric transducers of diameter $30\text{ mm}$ in direct contact with the grains are used as an acoustic source and for detection.
我们的声学测量是在一个直径为 $60\text{ mm}$、高度为 $H$ 的金属圆柱形室中的颗粒介质里进行的(图 1)。颗粒介质由平均直径分别为 $1.5$ 和 $1.8\text{ mm}$ 的多分散玻璃珠或沙粒组成。样品厚度定义为颗粒层数 $L = H/d$。直径为 $30\text{ mm}$ 的宽带压电换能器与颗粒直接接触,用作声源和检测。
The influence of the sample size on the sound velocity and on the solid volume fraction was investigated for 6 or 7 different heights. For each height, 20 independent experiments were performed as follows: first, before each experiment, the granular medium was weighted and freshly poured in the container. Second, a reproducible packing was obtained by performing a single loading-unloading to $P = 352\text{ kPa}$, after which the confining pressure was set and the height of the sample was measured ($\Delta H/H = \Delta L/L$ ∼ $0.1$%).
研究了 $6$ 或 $7$ 个不同高度的样品大小对声速和固体体积分数的影响。针对每种高度,进行了 $20$ 次独立实验,具体如下:首先,在每次实验前,将颗粒介质称重并重新倒入容器中。其次,通过一次装载-卸载获得可重现的堆积,装载-卸载到 $P = 352\text{ kPa}$,然后设定约束压力并测量样品的高度($\Delta H/H = \Delta L/L$ ∼ $0.1$%)。
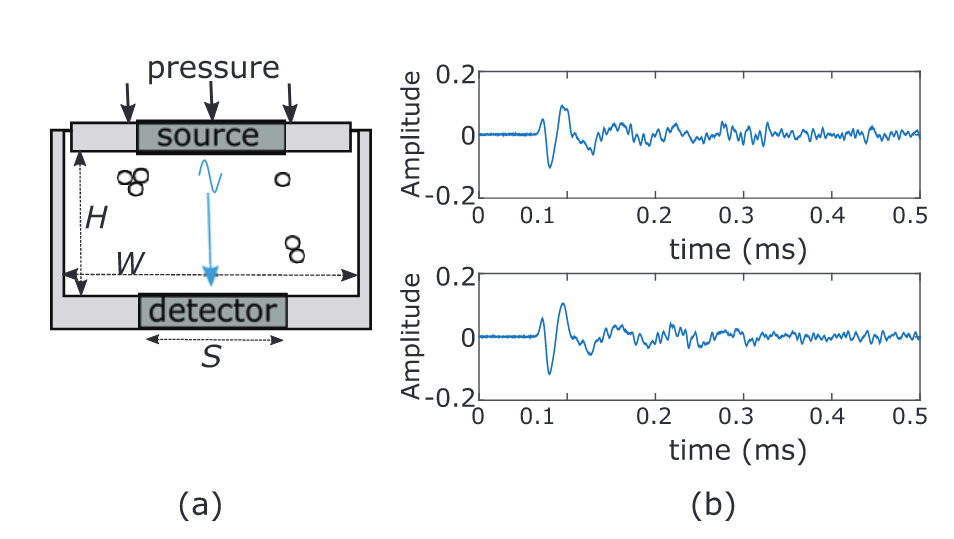
(Color online) Schematic of the setup used in the linear-sound experiments. (a) Glass beads of $d = 1.5\text{ mm}$ are contained in a metal cell with a width, $D$, of 60 mm and a variable height, $H$. A pressure is applied via a piston and a piezoelectric transducer placed in the piston serves as acoustic source by sending a short pulse. The propagating wave is measured by a same transducer of size $S$ = 30 mm, placed at the bottom of the cell. (b) Typical short sound pulses (broadband) propagating through two different packings of $H$ ~ 55 mm and at a confining pressure of 352 kPa are shown.
(彩色在线) 线性声学实验装置示意图。(a) 在一个宽度为 $D = 60\text{ mm}$、高度为 $H$ 可变的金属室中装有 $d = 1.5\text{ mm}$ 的玻璃珠。通过活塞施加压力,置于活塞中的压电换能器通过发送短脉冲作为声源。传播的声波由放置在电池底部的尺寸为 $S = 30\text{ mm}$ 的相同传感器测量。(b) 图中显示了典型的短声脉冲(宽带)在 $352\text{ kPa}$ 的约束压力下通过两个不同的堆积($H\sim 55\text{ mm}$)传播的情况。
Acoustic measurements were performed by sending a single short pulse of $0.1 \mu\text{s}$ and an amplitude of $100\text{ mV}$ every $50\text{ ms}$ using a longitudinal piezoelectric transducer of $30\text{ mm}$ in diameter, broadband between $10$ and $1000\text{ kHz}$ (centered at $500\text{ kHz}$). The sound transmission was detected by a similar transducer at a distance $L$ from the source and was averaged over about $3\text{ s}$. Typical coherent sound pulses propagating through a glass bead packing of 38 layers under a confining pressure $P = 352\text{ kPa}$ are shown in fig. 1(b).
声学测量是通过使用一个直径为 $30\text{ mm}$ 的纵向压电传感器,每隔 $50\text{ ms}$ 发送一个 $0.1 \mu\text{s}$ 和振幅为 $100\text{ mV}$ 的单个短脉冲来实现的,该传感器的宽带范围在 $10$ 和 $1000\text{ kHz}$ 之间(以 $500\text{ kHz}$ 为中心)。声音传输由距离声源 $L$ 的类似传感器检测,平均时间约为 $3\text{s}$。图 1(b) 显示了在约束压力 $P = 352\text{ kPa}$ 下,通过 $38$ 层玻璃珠堆积传播的典型相干声脉冲。
The associated spectra are centered at $f = 40\text{ kHz}\sim 1/T$ with $T\sim 25\mu\text{s}$ the pulse duration where the high-frequency component is filtered by the scattering attenuation of the longitudinal sound pulse. We determined the sound velocity from the arrival time of the first peak, which is about $V_{L} = 750\text{ m/s}$. The first peak of the coherent front is associated with the self-averaged longitudinal wave; its wavelength $\lambda_{L} = V_{L}/f\sim 18.7\text{ mm}$ is much larger than the particle size $\lambda_{L} \geq 10d$.
The solid volume fraction $\phi$ was also calculated from the mass of the granular medium; the volume (obtained from the diameter and the measured height) of the container and the density of the constituent medium ($\rho_{\text{glass}} = 2600\text{ kg/m}^3$, $\rho_{\text{sand}} = 2650\text{ kg/m}$3).
相关频谱以 $f = 40\text{ kHz}\sim 1/T$ 为中心,其中 $T\sim 25\mu\text{s}$ 为脉冲持续时间,高频成分在此被纵波声脉冲的散射衰减所过滤。我们根据第一个峰值的到达时间确定了声速,大约为 $V_{L} = 750\text{ m/s}$。相干前沿的第一个峰值与自平均纵波(压缩波 )有关;其波长为 $\lambda_{L} = V_{L}/f\sim 18.7\text{ mm}$ ,远大于粒径 $\lambda_{L}\geq 10d$。
固体体积分数 $\phi$ 也是根据颗粒介质的质量、容器的体积(根据直径和测量高度得出)以及组成介质的密度($\rho_{\text{glass}} = 2600\text{ kg/m}^3$, $\rho_{\text{sand}} = 2650\text{ kg/m}^3$)计算得出的。
Fluctuations in the packing density
First, we investigated the ensemble-averaged packing density, $\bar{\phi}$, as a function of $L$ for three different $P$ . We observed that the average $\phi$ decreases with decreasing number of layers and this decrease appears independent of $P$ (fig. 2(a2)). The change in $\bar{\phi}$ is of the order of 4% and is likely due to the contact mismatch between the spherical beads and the interface of the wall-top and wall-bottom boundary of the container. This mismatch is more important for fewer bead layers as the ratio between the bead-bead contacts and the bead-interface contacts decreases.
首先,我们研究了三种不同 $P$ 的系综平均堆积密度 $\bar{\phi}$ 与 $L$ 的函数关系。我们观察到, $\phi$ 平均值随着层数的减少而减少,而且这种减少似乎与 $P$ 无关(图 2(a2))。$\bar{\phi}$ 的变化量级为 4%,可能是由于球形珠子与容器壁顶和壁底边界界面之间的接触不匹配造成的。随着珠子与珠子之间的接触和珠子与表面接触之间的比例降低,这种不匹配在珠子层数较少的情况下更为重要。
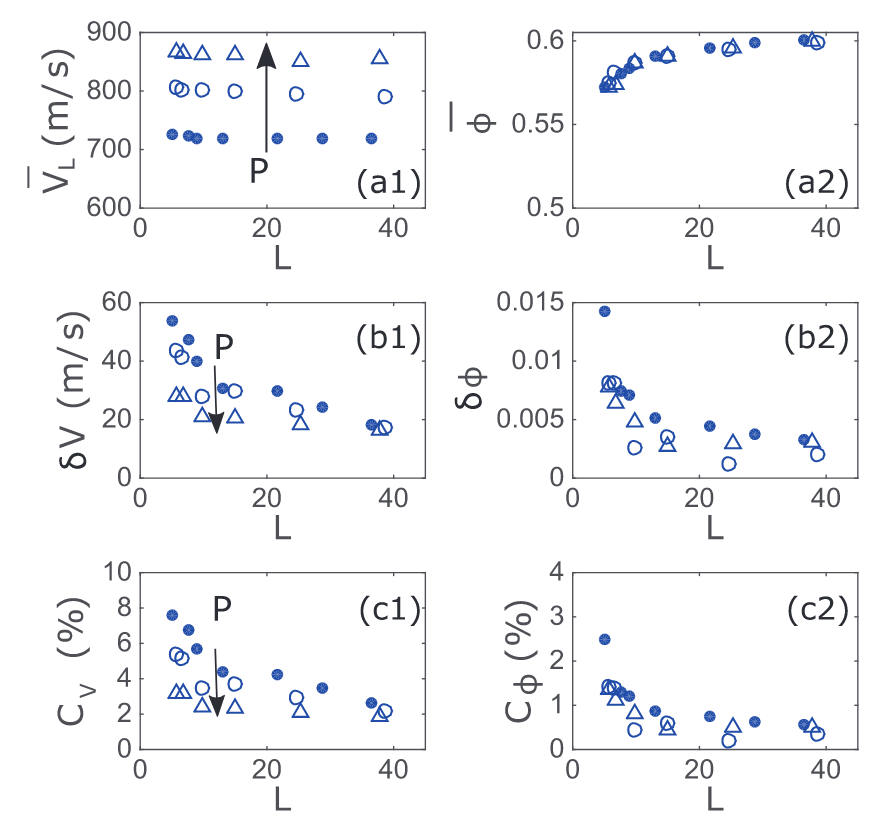
(Color online) Influence of the sample size $L$ and confining pressure $P$ for spherical glass grains. (a1) Average sound velocity $\bar{V}_{L}$. (b1) Standard deviation of the sound velocity ($\delta V_{L}$). (c1) Fluctuation in the sound velocity $C_{V}$ . (a2) Average solid volume fraction $\bar{\phi}$. (b2) Standard deviation of the solid volume fraction ($\delta\phi$) and (c2) Fluctuation in solid volume fraction $C_{\phi}$. The relative fluctuations are calculated from the ratio of standard deviation to the mean value. Different symbols indicated the different confining pressures: $177\text{ kPa}$ in points, $354\text{ kPa}$ in open circles and $532\text{ kPa}$ open triangles.
(彩色在线)对于球形玻璃颗粒,样品尺度 $L$ 和约束压力 $P$ 的影响。(a1) 平均声速 $\bar{V}_{L}$。(b1) 声速的标准偏差($\delta V_{L}$)。(c1) 声速波动 $C_{V}$ 。 (a2) 平均固体体积分数 $\bar{\phi}$.(b2) 固体体积分数的标准偏差($\delta\phi$)和 (c2) 固体体积分数的波动 $C_{\phi}$。相对波动由标准偏差与平均值之比计算得出。不同符号表示不同的约束压力:点表示 $177\text{ kPa}$,圆圈表示 $354\text{ kPa}$,三角形表示 $532\text{ kPa}$。
Furthermore, the results show that the standard deviation in $\phi$ increases with decreasing number of layers (fig. 2(b2)) and seems independent of the confining pressure.
The calculated relative fluctuations in the packing density $C_{\phi}$ increase with decreasing the sample size and appear independent on the confining pressure (fig. 2(c2)). A relatively large system of about 40 layers shows a variation in $\phi$ of ~ $0.5$%, whereas for thin packings consisting of less than 10 layers this fluctuation increases to almost 2–3%.
此外,结果显示 $\phi$ 的标准偏差随着层数的减少而增加(图 2(b2)),并且似乎与约束压力无关。
计算得出的堆积密度 $C_{\phi}$ 的相对波动随着样品尺度的减小而增大,并且似乎与约束压力无关(图 2(c2))。一个由大约 $40$ 层组成的相对较大的系统显示的 $\phi$ 变化率约为 $0.5$%,而对于由少于 $10$ 层组成的薄填料,这种波动增加到近 $2-3$%。
The similarity in the fluctuation in $\phi$ between the experiments at different confining pressures is likely due to the pre-loading, which produces a stable reproducible packing that is almost independent of our final confining pressure, explaining also why the average $\phi$ is independent of the confining pressure in our experiments.
在不同约束压力下的实验中,$\phi$ 的波动相似,这可能是由于预加载产生了稳定的可复现堆积,而这种堆积几乎与我们的最终约束压力无关,这也解释了为什么在我们的实验中平均 $\phi$ 与约束压力无关。
Fluctuations in the sound velocity
From the sound propagation measurements we find that the ensemble-averaged sound velocity $\bar{V}_{L}$ (we will use the overline to indicate ensemble-averaged values) shows no clear dependence on the sample thickness (fig. 2(a1)) , but it increases as a function of the confining pressure as predicted by the mean-field theory, roughly as $V_{L} \propto P^{1/6}$. Furthermore, the standard deviation of the sound velocity shows a clear increase with a decrease of the sample thickness and the magnitude of this increase is dependent on the confining pressure.
从声音传播的测量结果中我们发现,系综平均声速 $\bar{V}_{L}$(我们将使用上划线来表示系综平均值)与样品厚度没有明显的依赖关系(图 2(a1)),但正如平均场理论所预测的那样,它是约束压力的函数,大致随着 $V_{L} \propto P^{1/6}$ 的增加而增加. 此外,声速的标准偏差随着样品厚度的减小而明显增大,增大的幅度取决于约束压力。
To compare the fluctuations at the different confining pressures we calculated the relative fluctuation in the sound velocity $C_{V}$ (fig. 2(c2)). The $C_{V}$ shows a clear increase for decreasing the sample thickness $L$. For a relatively large system, of about 40 layers, the fluctuation is $C_{V}$ ~ 2%, whereas for smaller systems involving less than 10 layers, this fluctuation increases rapidly to almost 8%. Importantly, $C_{V}$ decreases with increasing confining pressure. Although the increase of the relative fluctuations $C_{V}$ and $C_{\phi}$ is of similar magnitude, the absolute fluctuation of the sound velocity is about 5 times larger than that of the solid volume fraction.
为了比较不同约束压力下的波动,我们计算了声速 $C_{V}$ 的相对波动(fig.2(c2)). 随着样品厚度 $L$ 的减小,声速 $C_{V}$ 明显增加。对于一个相对较大的系统(约 $40$ 层),其波动为 $C_{V}\sim 2$%,而对于涉及少于 $10$ 层的较小系统,其波动则迅速增加到近 $8$%。重要的是,$C_{V}$ 会随着约束压力的增加而减小。虽然相对波动 $C_{V}$ 和 $C_{\phi}$ 的增加幅度相似,但声速的绝对波动比固体体积分数的波动大 $5$ 倍左右。
Influence of particle shape on fluctuations in $V_{L}$ and $\phi$.
Since the particle angularity and the aspect ratio are important parameters, we expect that the relative fluctuations may also depend on the particle shape. Therefore, we investigated the fluctuations in $V_{L}$ and $\phi$ in experiments conducted with the sand particles at $P = 177\text{ kPa}$. In packings of sand particles, the sound velocity and the average solid volume fraction are much lower than in packings of glass beads (fig. 3(a2) and (b2)). This is likely due to the interlocking effect of the angular particles that stabilizes the packings with a lower $Z$.
由于颗粒角度和长宽比是重要参数,我们预计相对波动也可能取决于颗粒形状。因此,我们在 $P = 177\text{ kPa}$ 条件下对沙粒进行了实验,研究了 $V_{L}$ 和 $\phi$ 的波动情况。在沙粒堆积中,声速和平均固体体积分数远低于玻璃珠堆积(图 3(a2) 和 (b2))。这可能是由于有角颗粒的互锁效应使堆积稳定在较低的 $Z$。
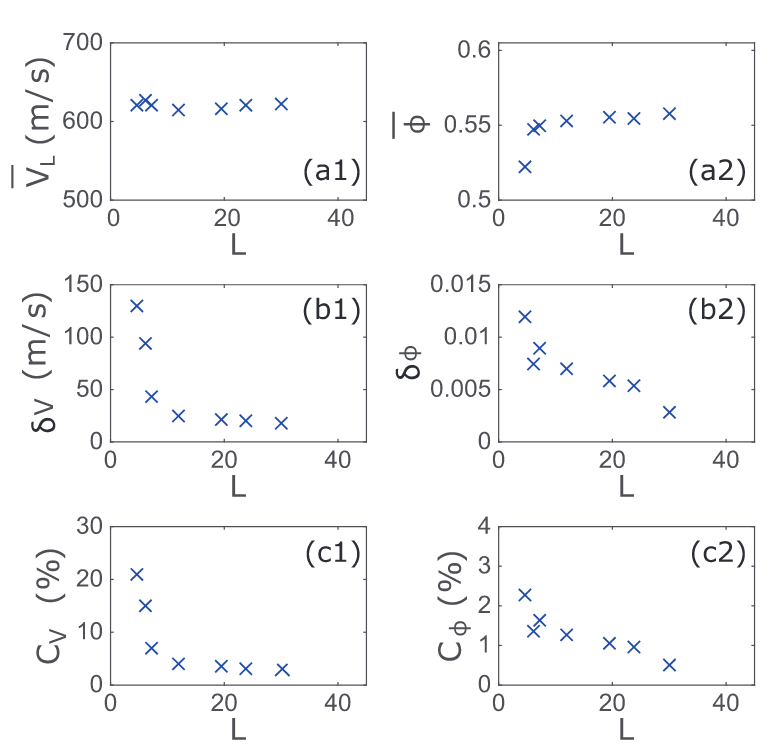
(Color online) Influence of the sample size $L$ and the particle shape ($P = 177\text{ kPa}$) for sand grains. (a1) Average sound velocity, $\bar{V}_{L}$. (b1) Standard deviation of the sound velocity $\delta V$ . (c1) Fluctuation in the sound velocity $C_{V}$ . (a2) Average solid volume fraction, $\bar{\phi}$. (b2) Standard deviation of the solid volume fraction $\sigma_{\phi}$. (c2) Fluctuation in solid volume fraction $C_{\phi}$.
(彩色在线)样本大小 $L$ 和颗粒形状($P = 177\text{ kPa}$)对沙粒的影响。(a1) 平均声速,$\bar{V}_{L}$。(b1) 声速的标准偏差 $\delta V$ 。 (c1) 声速的波动 $C_{V}$ 。 (a2) 平均固体体积分数,$\bar{\phi}$。(b2) 固体体积分数的标准偏差 $\sigma_{\phi}$ .(c2) 固体体积分数的波动 $C_{\phi}$。
Generally, the standard deviation of $V_{L}$ and $\phi$ grows as the sample size decreases. To compare the results in sand particle packings to those obtained in glass bead pack- ings we examined the fluctuations $C_{\phi}$ and $C_{V}$. First, the fluctuations in $\phi$ increase ~ 4 times for smaller samples, a result very similar to glass beads. Second, we observe that $C_{V}$ for sand increases significantly with decreasing layers (fig. 3(c1)). A relatively large system of about 30 layers shows a fluctuation $C_{V}$ ~ 2%, for smaller systems involving less than 10 layers, the fluctuation increase to almost 20%. This increase is more pronounced than the increase observed in glass beads packings. We attribute this effect to the nonspherical shape of sand particles which increases the disorder and the local elastic heterogeneities measured by a given coarse-graining length.
一般来说,随着样本大小的减小,$V_{L}$ 和 $\phi$ 的标准偏差也会增大。为了将沙粒堆积中的结果与玻璃珠堆积中的结果进行比较,我们研究了 $C_{\phi}$ 和 $C_{V}$ 的波动。首先,对于较小的样品,$\phi$ 的波动增加了 ~ $4$ 倍,这一结果与玻璃珠非常相似。其次,我们观察到砂的 $C_{V}$ 随着层数的减少而显著增加(图 3(c1))。一个由大约 $30$ 层组成的相对较大的系统显示出大约 $2$% 的 $C_{V}$ 波动,而对于少于 $10$ 层的较小系统,波动则增加到近 $20$%。这种增加, 比在玻璃珠堆积中观察到的增加, 更为明显。我们将这一效应归因于砂粒的非球形形状,它增加了无序性和在给定粗粒化长度下测量到的局部弹性异质性。
Numerical simulation
Model
We modeled granular media by means of compressed 2D hexagonal packings of frictionless spherical particles with same radius $R$ (fig. 4(a)). The overlap of the particles at position $\vec{r}_{i}$ and $\vec{r}_{j}$ is given by $\delta_{ij} = 2R - |\vec{r}_{i} - \vec{r}_{j}|$ (and $R_{i} = R_{j} = R$). For $\delta_{ij} > 0$, the contact force follows from the Hertzian contact law $F_{ij} = \epsilon\cdot\delta_{ij}^{3/2}$; otherwise $F_{ij} = 0$.
我们通过无摩擦球形颗粒的压缩二维六边形堆积来模拟颗粒介质,这些颗粒的半径都为 $R$(图 4(a))。颗粒在位置 $\vec{r}_{i}$ 和 $\vec{r}_{j}$ 上的重叠度为 $\delta_{ij} = 2R - |\vec{r}_{i} - \vec{r}_{j}|$(且 $R_{i} = R_{j} = R$)。对于 $\delta_{ij}>0$,接触力来自 Hertz 接触定律 $F_{ij} = \epsilon\cdot\delta_{ij}^{3/2}$ ;否则 $F_{ij} = 0$。
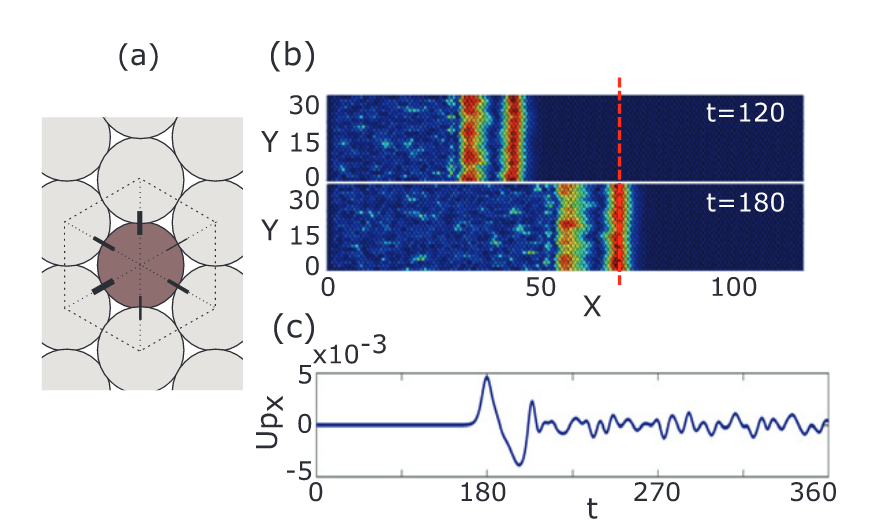
(Color online) (a) Schematic of a 2D hexagonal packing, the darker particle has 6 contacts. (b) Two snapshots at time $t = 120$ and $t = 180$ (in a.u.) of a one-cycle sinusoidal pulse propagating through a 2D hexagonal packing of frictionless spheres with disorder $\sigma_{g} = 0.2$. The color of the sphere represents its total velocity, defined as $Up_{t} = \sqrt{Up_{x}^{2} + Up_{y}^{2}}$ ranging 0 (dark blue) to max (red). (c) The $x$-component of one-cycle sinusoidal pulse propagation measured at a distance $X$ (or $L$) $= 120$ from the source.
(彩色在线) (a) 二维六角堆积示意图,深色粒子有 6 个接触点。(b) 在时间 $t = 120$ 和 $t = 180$(单位为 a.u.)处的两个快照,一个周期正弦脉冲在无序度为 $\sigma_{g} = 0.2$ 的无摩擦球体的二维六角堆积中传播。球体的颜色代表其总速度,定义为 $Up_{t} = \sqrt{Up_{x}^{2}+ Up_{y}^{2}}$ 从 0(深蓝色)到 max(红色)。(c) 在距离声源 $X$(或 $L$)$= 120$ 处测得的单周期正弦波脉冲传播的 $x$ 分量。
Here $\epsilon$ is a stiffness constant and depends on the material properties and the contact curvature. We used 2D packings whose sizes vary from $10^{3}$ to more than $10^{4}$ particles. The hexagonal packings were prepared at an averaged particle overlap $\delta_{0}$ ~ 2% of the particle diameter and, for simplicity, the radius of the particles and $\epsilon$ were set to 1. Stiffness disorder was introduced into our packing by randomly picking the constant $\epsilon$ either from a Gaussian distribution with variable standard deviation $\sigma_{g}$ (0, 0.2 and 0.4) or from a uniform distribution \sigma_{u} between 0 and 1. In the latter case there are contacts present that do not carry force ($\epsilon = 0$).
这里的 $\epsilon$ 是一个刚度常数,取决于材料特性和接触曲率。我们使用的二维堆积的颗粒大小从 $10^{3}$ 到超过 $10^{4}$ 不等。六边形堆积的平均颗粒重叠度为颗粒直径的 $2$%,为简单起见,颗粒半径和 $\epsilon$ 均设为 $1$。通过从标准偏差可变的高斯分布 $\sigma_{g}$ ($0$、$0.2$ 和 $0.4$)或介于 $0$ 和 $1$ 之间的均匀分布 $\sigma_{u}$ 中随机选取常数 $\epsilon$ ,在我们的堆积中引入了无序刚度。在后一种情况下,存在不受力的接触($\epsilon = 0$)。
Note that such a numerical model mimics the experimental realization of a 2D triangular lattice of elastic spheres under compression in which sound propagation revealed an inhomogeneous contact network (due to the imperfection of bead contacts despite the regular packing) similar to that in a 3D disordered bead packing.
Notice that no damping at the contacts is included in our simulation of coherent sound propagation as the attenuation of this wave is expected to be dominated by scattering. We have also performed simulation in which disorder was introduced via the mass of the particles, $m$, while keeping $\epsilon = 1$. In these simulations, we observed a similar qualitative behavior as for the case of random distribution of $\epsilon$ (data not shown).
需要注意的是,这种数值模型模拟了二维三角弹性球晶格在压缩条件下的实验实现,在这种实验中,声音传播体现了一个不均匀的接触网络(由于珠子接触不完美,尽管有规则的堆积),类似于三维无序珠子堆积。
请注意,我们在模拟相干声传播时没有考虑接触处的阻尼,因为预计这种声波的衰减主要是由散射引起的。我们还进行了模拟,在保持 $\epsilon = 1$ 的情况下,通过粒子质量 $m$ 引入了无序。在这些模拟中,我们观察到了与 $\epsilon$ 随机分布情况类似的定性行为(数据未展示)。
We employed periodic boundary conditions in the $Y$-direction and a fixed boundary on the right edge of the system by setting, at this boundary, the components of the particle velocity in the $X$-direction to zero.
In order to compare our simulations to our experiments we excited the particles at the left edge of the system by a single sinusoidal compression in the $X$-direction. The subsequent motion of the particles was obtained by numerical integration of Newtons equations of motion. In every time step the acceleration of the $i$-th particle is $\ddot{\vec{r}_{i}} = \vec{F}_{i}/m_{i}$ where $\vec{F}_{i} = \sum_{j\neq i}\vec{F}_{ij}$. Furthermore, $X$ is made dimensionless by dividing by the particle diameter and the time is made dimensionless by multiplying with the characteristic frequency $f_{0}\sim (k/m)^{1/2}$ with the contact stiffness $k = (3/2)\epsilon\delta_{0}^{1/2}$.
我们在 $Y$ 方向上采用了周期性边界条件,并在系统的右边缘采用了固定边界,即在该边界上将粒子在 $X$ 方向上的速度分量设为零。
为了将模拟结果与实验结果进行比较,我们对系统左侧边缘的粒子在 $X$ 方向上进行了单次正弦激发。粒子随后的运动是通过对牛顿运动方程进行数值积分得到的。在每个时间步长中,第 $i$ 个粒子的加速度为 $\ddot{\vec{r}_{i}} = \vec{F}_{i}/m_{i}$,其中 $\vec{F}_{i} = \sum_{j\neq i}\vec{F}_{ij}$。此外,$X$ 方向通过除以颗粒直径实现无量纲化,时间通过乘以特征频率 $f_{0}\sim (k/m)^{1/2}$ 与接触刚度 $k = (3/2)\epsilon\delta_{0}^{1/2}$ 实现无量纲化。
Typical sound traces of the particle velocity, i.e., snapshots, are shown in fig. 4(b). Next, coherent sound signals were obtained by averaging the $X$-velocity component of all the particles along the $Y$-direction that are at a given distance $X$ (or $L$) from the source, hence mimicking the large contact area of the transducer (fig. 4(c)). The wavelength $\lambda_{L}$ is about $40d$ and the sound velocity is determined from the time of arrival of the first peak. We investigated 4 scenarios with varying disorder ranging from $\sigma_{g} = 0$, systems without disorder, to the most disordered systems in which $\epsilon$ is obtained from the uniform distribution.
粒子速度的典型声迹,即快照,如图 4(b)所示。接下来,通过平均所有与声源保持一定距离$X$(或$L$)的粒子沿 $Y$ 方向的 $X$ 速度分量,从而模拟换能器的大接触面积,获得相干的声音信号(图 4(c))。波长 $\lambda_{L}$ 约为 $40d$,声速根据第一个峰值的到达时间确定。我们研究了 4 种不同无序度的情况,从无序度为 $\sigma_{g} = 0$ 的系统到最无序的系统 ($\epsilon$ 是通过均匀分布获得的).
For each scenario we simulated 20 packings and evaluated, similar to the experiments, the mean longitudinal sound velocity, its standard deviation and its relative fluctuation. The results shown here are obtained in packings that consist of 300 particles in the $X$-direction and 40 in the $Y$-direction. We have tested packings of various width-to-length ratios and found similar results (see below).
对于每种情况,我们模拟了 $20$ 个堆积,并对平均纵向声速、其标准偏差和相对波动进行了与实验类似的评估。这里显示的结果是由 $300$ 个 $X$ 方向和 $40$ 个 $Y$ 方向的颗粒组成的堆积得到的。我们还测试了不同宽度-长度比的堆积,发现了类似的结果(见下文)。
Sound propagation
We expect that the experimentally observed increase of fluctuations in $V_{L}$ for thin samples is associated with the elastic heterogeneities in granular packings. To confirm this scenario, we simulated longitudinal sound propagation in 2D hexagonal packings of particles in which disorder was introduced via the random stiffness $\epsilon$ of the contacts between the particles giving rise to the local fluctuation of the sound velocity $V$ ∼ $(\epsilon/m)^{1/2}$.
我们预计,实验观察到的薄样品中 $V_{L}$ 涨落的增加与颗粒堆积中的弹性异质性有关。为了证实这一点,我们模拟了声音在二维六边形颗粒堆积中的纵波传播,其中通过颗粒间接触的随机刚度 $\epsilon$ 引入了无序,从而导致声速 $V$ ∼ $(\epsilon/m)^{1/2}$ 的局部波动。
The stiffness disorder in the simulated packings is varied by randomly pulling from a Gaussian distribution with a given width $\sigma_{g}$ or from a uniform distribution ($\sigma_{u}$) between 0 and 1. The degree of constact stiffness disorder ranges from $\sigma_{g} = 0$ (corresponding to no disorder), $\sigma_{g} = 0.2$, $\sigma_{g} = 0.4$, to $\sigma_{u}$ the most disordered system in which is obtained from the uniform distribution. For each of these four scenarios we simulated 20 packings that were excited by a sinusoidal compressional pulse. As in the experiments, the velocity of the sound pulse was determined from the arrival time of the first peak in the time trace of the particle velocities shown in fig. 4 (accurate determination of the phase velocity can be found in [22]).
通过从给定宽度为 $\sigma_{g}$ 的高斯分布或从 $0$ 到 $1$ 之间的均匀分布($\sigma_{u}$)中随机抽取,可以改变模拟堆积中的刚度无序度。恒定刚度的无序程度从 $\sigma_{g} = 0$(对应于无序)、$\sigma_{g} = 0.2$、$\sigma_{g} = 0.4$ 到 $\sigma_{u}$,其中最无序的系统是从均匀分布中得到的。在这四种情况下,我们分别模拟了 $20$ 个由正弦压缩脉冲激发的堆积。与实验中一样,声脉冲的速度是根据图 4 所示粒子速度时间轨迹中第一个峰值的到达时间确定的(相位速度的精确测定可参见文献 [22])。
The results obtained from the simulation (in arbitrary unit) are presented in fig. 5. First, note that the average velocity is slightly dependent on the sample size, with an increase of about 3% for thicker samples. A similar increase has also been observed in [23,26]. The standard deviation shows a much more important increase of about 200% for thin samples. In systems without disorder, $\sigma_{g} = 0$, there are, as expected, no fluctuations in the measured sound velocity.
模拟得出的结果(任意单位)见图 5。首先要注意的是,平均速度与样本尺度略有关系,样本越厚,平均速度增加约 $3$%。在文献[23,26]中也观察到类似的增长。对于较薄的样品,标准偏差显示了更显著的增长,约为 $200$%。在没有无序的系统中,即 $\sigma_{g} = 0$,观测到的声速没有波动。
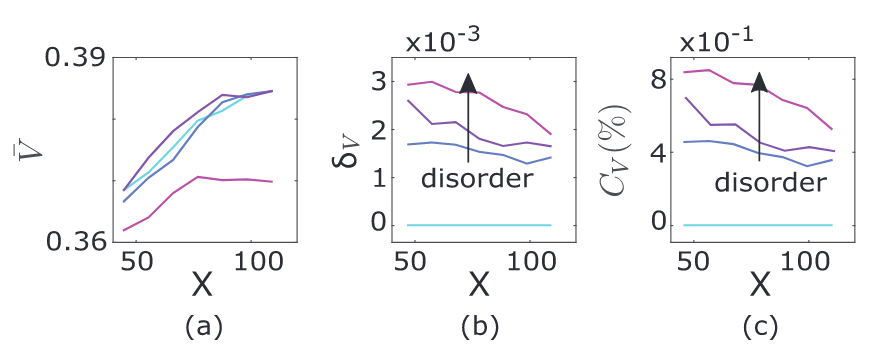
(Color online) Influence of sample size and contact stiffness disorder in numerical models of 2D hexagonal packings of spheres. (a) Average sound velocity $\bar{V}$ (in a.u.). (b) Standard deviation of the sound velocity $\delta V_{L}$ (in a.u.). (c) Relative fluctuation in the sound velocity $C_{V} = \delta V_{L}/\bar{V}_{L}$, for increasing disorder $\sigma_{g} = 0$, $\sigma_{g} = 0.2$, $\sigma_{g} = 0.4$ and $\sigma_{u}$.
(彩色在线)二维六角球体堆积数值模型中样本大小和接触刚度的影响。(a) 平均声速 $\bar{V}$ (单位 a.u.)。(b) 声速的标准差 $\delta V_{L}$(单位 a.u.)。(c) 当无序度以 $\sigma_{g} = 0$、$\sigma_{g} = 0.2$、$\sigma_{g} = 0.4$ 和 $\sigma_{u}$ 增加时,声速 $C_{V} = \delta V_{L}/\bar{V}_{L}$ 的相对波动。
Instead, when disorder is introduced, the simulations display a relative fluctuation in $V_{L}$ which increases with decreasing sample size, similar to what was observed in the experiments (fig. 2(c1) and fig. 3(c1)). Note that here the wavelength is comparable to or smaller than the sample size and hence the coarse-graining length would be determined by $\lambda_{L}$; nevertheless, increasing the sample size for a given configuration may reduce the fluctuations by the self-averaging procedure.
相反,当引入无序时,模拟结果显示 $V_{L}$ 的相对波动会随着样本大小的减小而增大,这与实验中观察到的情况类似(图 2(c1) 和图 3(c1))。请注意,这里的波长与样本大小相当或更小,因此粗粒化长度将由 $\lambda_{L}$ 决定;尽管如此,对于给定构型,增加样本大小可能会通过自平均处理减少波动。
Additionally, we find that for increasing disorder the relative fluctuations of the sound velocity increase, indicating that the increase of disorder in our simulations (fig. 5) has a similar effect on the sound velocity as a decrease of the pressure in our experiments (fig. 2(c1)). We plan to investigate this issue in the future with 3D simulations.
此外,我们还发现,随着无序度的增加,声速的相对波动也会增加,这表明在我们的模拟中(图 5),无序度的增加对声速的影响类似于我们实验中(图 2(c1))压力的降低。我们计划今后通过三维模拟来研究这个问题。
Discussion
As mentioned in the introduction, sound velocity measurements provide an efficient method to determine the macroscopic elastic moduli of a granular packing in the long-wavelength limit. In this limit, the coarse graining is determined by the wavelength which is much larger than the particle size ($\lambda_{L} \geq 10d$) and also larger than the mesoscopic length ($\lambda_{L} > \xi$). To investigate the applicability of continuum elasticity and the role of elastic heterogeneities on the local scale, we have conducted both sound experiments and simulations in thin granular packings. In such thin samples the coarse-graining length is determined by the sample thickness $L$ which is reduced to the mesoscopic scale $\xi$.
如引言所述,声速测量提供了一种有效的方法来确定颗粒堆积物在长波极限下的宏观弹性模量。在此极限下,粗粒度由波长决定,而波长远大于颗粒尺度($\lambda_{L} \geq 10d$),也大于介观长度($\lambda_{L} > \xi$)。为了研究连续弹性的适用性和弹性异质性在局部尺度上的作用,我们在薄颗粒堆积中进行了声学实验和模拟。在这种薄样品中,粗粒化长度由样品厚度 $L$ 决定,而样品厚度 $L$ 被简化为介观尺度 $\xi$。
The measurements of the sound velocity and the solid volume fraction as a function of the sample thickness $L$ clearly show that the fluctuation in $V_{L}$ and $\phi$ increases with decreasing $L$. Interestingly, we found that the fluctuations in $V_{L}$ are much larger than those in $\phi$ (fig. 2), indicating that the sound velocity should be sensitive to the disorder in both the packing geometry and the contact stiffness network, while the packing density is only sensitive to the disorder of the packing geometry.
When the confining pressure increases the resulting elastic heterogeneity decreases. This picture is supported by our numerical simulations of sound propagation in a heuristic model of 2D hexagonal packings which show that the presence of disorder via a random stiffness of the contacts between the particles indeed leads to fluctuations in the coherent longitudinal sound velocity.
声速和固体体积分数与样品厚度 $L$ 的函数关系的测量结果清楚地表明,随着 $L$ 的减小,$V_{L}$ 和 $\phi$ 的涨落也随之增大。有趣的是,我们发现 $V_{L}$ 的涨落远大于 $\phi$ 的涨落(图 2),这表明声速对堆积几何形状和接触刚度网络的无序性都很敏感,而堆积密度只对堆积几何形状的无序性敏感。当束缚压力增加时,所产生的弹性异质性就会降低。我们对二维六角堆积启发式模型中的声音传播进行了数值模拟,结果表明,通过颗粒间接触的随机刚度而产生的无序确实会导致相干纵向声速的波动。
Such fluctuations appear particularly important for thin samples where the elastic heterogeneity cannot be sufficiently smeared out and continuum elasticity is expected to break down on small length scales. Moreover, the experimental observation of the pressure-dependent elastic heterogeneity is consistent with the numerical simulation.
Indeed, the similar effects on the sound velocity fluctuation between increasing disorder (simulations) or decreasing confining pressure (experiments) could be rationalized by the transition in the distribution of contact forces from Gaussian to exponential. Makse et al. showed that this transition is associated with the force chains more localized as the confining pressure is decreased. The localization of force chains is directly related to the local elastic heterogeneities, thus resulting in the large fluctuations observed in $V_{L}$ as compared to those in $\phi$.
这种波动对于薄样品尤为重要,因为在薄样品中,弹性异质性无法被充分抹平,而连续弹性预计会在小长度尺度上被破坏。此外,实验观察到的随压力变化的弹性异质性与数值模拟是一致的。
事实上,增加无序性(模拟)或降低束缚压力(实验)对声速波动的类似影响,可以通过接触力分布从高斯分布到指数分布的转变得到合理解释。Makse 等人的研究表明,随着束缚压力的降低,这种转变与力链更加局部化有关。力链的局部化与局部弹性异质性直接相关,从而导致在 $V_{L}$ 中观察到的波动比在 $\phi$ 中的波动大。
On the other hand, it has been shown that the local elastic heterogeneities may be related to the characteristic length scales, $l^{*}$ or $\xi$, which are controlled by the excess number of the contact to the isostatic limit $\Delta Z_{\text{iso}}$, i.e., the onset of rigidity. For frictionless sphere packings, theoretical and numerical considerations indicate that $l$ diverges at the jamming point as $l^{*}\sim \Delta Z_{\text{iso}}^{−1}\sim P^{−1/3}$. To evaluate directly the length scale $l^{*}$, Ellenbroek et al. investigated the fluctuation of the force response of a given 2D frictional packing to a zero-frequency localized perturbation or global shear.
另一方面,研究表明,局部弹性异质性可能与特征长度尺度 $l^{*}$ 或 $\xi$ 有关,这些长度尺度由接触到等静压极限 $\Delta Z_{\text{iso}}$ 的过剩数量控制,即刚性的开始。对于无摩擦的球形堆积,理论和数值计算表明,当 $l^{*}\sim \Delta Z_{\text{iso}}^{-1}\sim P^{-1/3}$ 时,$l$ 会在堵塞点发散。为了直接评估长度尺度 $l^{/*}$,Ellenbroek 等人研究了给定二维摩擦堆积对零频率局部扰动或全局剪切的力响应波动。
Using a Gaussian coarse-graining function and ensemble averaging over different observation points, they showed that the relative standard deviation of the shear stress (normalized to the mean stress) to a global shear deformation decreases inversely with the coarse-graining length $\xi$ and the data for different pressure can be collapsed by a rescaling with $\xi^{*}\Delta Z_{\text{iso}}$ implying $\xi^{*}\sim \Delta Z_{\text{iso}}^{−1}\sim P^{−1/3}$.
使用高斯粗粒化函数和不同观测点的系综平均、他们的研究表明,剪切应力(归一化为平均应力)与全局剪切变形的相对标准差随粗粒度长度 $\xi$ 的增加而反向减小,不同压力下的数据可以通过 $\xi^{*}\Delta Z_{\text{iso}}$ 的重定标进行折叠,这意味着 $\xi^{*}\sim \Delta Z_{\text{iso}}^{-1}\sim P^{-1/3}$。
Let us now examine if there is a relevant characteristic length scale in our confined frictional granular packings. First, we point out that the pressure-dependent fluctuation in the sound velocity VL = ((K + 4/3G)/ρ)1/2 may arise from the relative fluctuations both in the bulk modulus δK/K¯ and the shear modulus δG/G¯. However, as revealed by numerical simulations, the sound veloc- ity fluctuation CV = δVL/V¯L measured on small length scales should be primarily related to the heterogeneity in the shear modulus which is far more pronounced than in the bulk modulus due to the nonaffine deformation [18]. We may thus estimate the shear modulus fluctuation by δG ∼ (3/2)(K¯ + 4/3G¯)(δVL/V¯L). For the confining pres- sure P ∼ 200 kPa considered here, the previous measure- ment of the longitudinal and transverse sound velocities provides a ratio K¯ /G¯ = (V¯L/V¯T )2 − 4/3 = 1.89 with V¯L/V¯T ∼ 1.79 [21]. This leads to a relative fluctua- tion of the shear modulus δG/G¯ ∼ 5(δVL/V¯L), which may rise up to about 40% for a coarse-graining scale w = L ≤ 5 (fig. 6), indicating the breakdown of con- tinuum elasticity on a mesoscopic length scale ξ < 10d. This observation is consistent with numerical simulations investigating the spatial fluctuations both in the shear modulus [18] and in the shear force field [14], due to the floppy-mode responses. Secondly, the plots of CV (in log scales, fig. 6) illustrate a decay following approximately L−1 with the sample thickness L (fig. 6(a)), in agree- ment with the numerical results obtained on the shear modulus fluctuation [18] and also consistent with the behavior of the above fluctuating force field. Note that the decay of the relative fluctuations δVL/V¯L ∼ L−1 for a given coarse-graining length L may be interpreted as a sum of spatially uncorrelated variables corresponding to a Gaussian-like distribution with finite variance [18]. Moreover, similar to previous work [14], we may have a reasonable collapse of the data of relative fluctuations CV for different confining pressures by multiplying the sam- ple thickness L by P α with α ∼ 0.8 (fig. 6(b)). This result suggests a possible characteristic length scale in our frictional granular packing which is roughly related to the pressure by ξ ∼ P −0.8. The difference between this scaling and the scaling l∗ ∼ P −1/3 [14] obtained by numerical simulations on frictionless sphere packings may be due to the friction (ΔZc > ΔZiso), the anisotropic effect and the possible boundary effect in our granular system.

