Abstract
We describe a precise phase velocity measurement of longitudinal sound waves in granular solids under stress. We observe an important difference of the phase velocity between the packings of glass beads and sand particles, which is likely due to the interlocking effect caused by the particle shape.
This effect can be captured by the contact coordination number using the effective medium theory. We also investigate the change of this coordination number in dry and wet granular packings, caused by cyclic loading or nonlinear sound transmission. These acoustic measurements show that the particle-level properties such as shape and friction significantly influence the response of jammed granular solids to external driving.
我们描述了在应力作用下对颗粒固体中的纵波相速度的精确测量。我们观察到玻璃珠和沙粒堆积之间的相速度存在很大差异,这可能是由于颗粒形状造成的连锁效应。
这种效应可以用有效介质理论中的接触配位数来捕捉。我们还研究了干性和湿性颗粒堆积在循环加载或非线性声音传播情况下接触配位数的变化。这些声学测量结果表明,颗粒级的特性(如形状和摩擦力)极大地影响了堵塞态颗粒固体对外部驱动的响应。
Introduction
Amorphous systems as diverse as glasses, colloids, foams and granular materials may be governed by the common concept of jamming. A jammed state emerges when the density of randomly packed particles is high enough so that the particles all interact with their neighbors and resist flow. Numerous simulations and experiments have revealed that the average number of contacts per particle, i.e., the coordination number $Z$ (mechanically loaded), plays an essential role in the physical behavior of a granular system.
玻璃、胶体、泡沫和颗粒材料等各种无定形系统都可能受 “堵塞” 这一常见概念的支配。当随机堆积颗粒的密度足够高,以至于所有颗粒都与相邻颗粒相互作用并抵抗流动时,就会出现堵塞状态。大量模拟和实验表明,每个颗粒的平均接触数,即配位数 $Z$(机械加载下),对颗粒系统的物理行为起着至关重要的作用。
As the packing density $\phi$ of an ensemble of frictionless spheres is increased above a critical jamming value $\phi_{c}$, the system has finite bulk elastic modulus via an abrupt jump in $Z$ to reach the isostatic value $Z_{I}$ . Above the jamming point, $Z$ grows as a power-law of the excess packing density. Experimental techniques, such as X-ray tomography, MRI and fluorescent confocal microscopy have recently been developed to investigate the local geometry and the particle motion.
当无摩擦球体聚集体的堆积密度 $\phi$ 增加到临界堵塞值 $\phi_{c}$ 以上时,系统的有限体弹性模量会通过 $Z$ 的突然跃迁达到等静态值 $Z_{I}$ 。在堵塞点之上,$Z$ 的增长与过量堆积密度成幂律关系。最近开发了 X 射线断层扫描、核磁共振成像和荧光共聚焦显微镜等实验技术,用于研究局部几何形状和粒子运动。
Granular materials are composed of individual macroscopic solid grains that interact via dissipative contact forces. For frictionless spheres, $Z_{I} = 2d$ with $d$ the dimension; for frictional spheres, $Z_{I}$ drops from $6$ to a lower value $d + 1 = 4$ in a 3D system.
In the jammed state, the mechanical properties depend to a large extent on the inhomogeneous contact force network. Photoelastic observations offer important insights in those contact forces during the jamming transition in 2D systems. However, in real 3D granular materials, the photoelastic method becomes more difficult to apply.
颗粒材料由各个宏观固体颗粒组成,这些颗粒通过耗散接触力相互作用。对于无摩擦的球体,$Z_{I} = 2d$,$d$ 为维数;对于有摩擦的球体,在三维系统中,$Z_{I}$ 从 $6$ 降至较低值 $d + 1 = 4$。
在堵塞态下,机械性质在很大程度上依赖于非均匀的接触力网络。在二维系统中,光弹性观测可提供有关堵塞转变期间接触力的重要见解。然而,在实际的三维颗粒材料中,光弹性方法变得更加难以应用。
Sound waves propagate through the contacts between grains, making sound an alternative and unique probe to examine the elastic and dissipative responses of the contacts inside 3D disordered granular materials. If the jammed granular material is treated as homogenous, for example by coarse graining, effective medium theories may be applied using an affine approximation to qualitatively connect the global response, like the bulk and shear elastic moduli $K_{\text{eff}}$ and $G_{\text{eff}}$, to the local geometry.
声波通过颗粒之间的接触传播,使声音成为研究三维无序颗粒材料内部接触的弹性和耗散响应的另一种独特探针。如果将堵塞的颗粒材料视为均质材料,例如通过粗粒化处理,则可以使用有效介质理论,使用近似方法定性地将全局响应(如体积和剪切弹性模量 $K_{\text{eff}}$ 和 $G_{\text{eff}}$)与局部几何形状联系起来。
In the case of isotropic compression, it was shown that,
$$ K_{\text{eff}}(P) = \frac{k_{n}}{12\pi}(\phi Z)^{\frac{2}{3}}\left(\frac{6\pi P}{k_{n}}\right)^{\frac{1}{3}}\\ G_{\text{eff}}(P) = \frac{k_{n} - \frac{3}{2}k_{t}}{12\pi}(\phi Z)^{\frac{2}{3}}\left(\frac{6\pi P}{k_{n}}\right)^{\frac{1}{3}} $$
where $P$ is the confining pressure, $k_{n} = 4G/(1 − \nu)$ and $k_{t} = 8G/(2 − \nu)$ are the normal and tangential stiffness (with $G$ the shear modulus and $\nu$ Poisson ratio for grain materials), $Z$ is the coordination number (assumed to be constant).
在各向同性压缩的情况下,结果表明
$$ K_{\text{eff}}(P) = \frac{k_{n}}{12\pi}(\phi Z)^{\frac{2}{3}}\left(\frac{6\pi P}{k_{n}}\right)^{\frac{1}{3}}\\ G_{\text{eff}}(P) = \frac{k_{n} - \frac{3}{2}k_{t}}{12\pi}(\phi Z)^{\frac{2}{3}}\left(\frac{6\pi P}{k_{n}}\right)^{\frac{1}{3}} $$
其中,$P$ 是约束压强,$k_{n} = 4G/(1 - \nu)$ 和 $k_{t} = 8G/(2 - \nu)$ 是法向和切向刚度(对于颗粒材料,$G$ 是剪切模量,$\nu$ 是泊松比),$Z$ 是配位数(假定为常数)。
The scaling of $K_{\text{eff}}$ and $G_{\text{eff}}$ can be determined by the speeds of compression and shear waves, via $V_{P} = \sqrt{(K_{\text{eff}} + 2G_{\text{eff}})/\rho_{0}}$ and $V_{S} = \sqrt{G_{\text{eff}}/\rho_{0}}$ where $\rho = \rho_{0}\phi$ and $\rho_{0}$ is the particle density.
It has been observed, however, that the sound speeds scale as $V\propto P^{1/4}$ at low $P$ and $V\propto P^{1/6}$ at high $P$ in jammed sphere packings (we will show that the experiments presented in this work remain in the $V\propto P^{1/6}$ regime).
This observation can be explained by the mechanism of contact recruitment via buckling of the grains under compression through slippage or by the non spherical contacts. On the contrary, the number of contacts can be reduced by shear loading, as evidenced by the sound speed measurement.
$K_{\text{eff}}$ 和 $G_{\text{eff}}$ 的缩放可以由压缩波和剪切波的速度决定、通过 $V_{P} = \sqrt{(K_{\text{eff}} + 2G_{\text{eff}})/\rho_{0}}$ 和 $V_{S} = \sqrt{G_{\text{eff}}/\rho_{0}}$ 其中 $\rho = \rho_{0}\phi$, 且 $\rho_{0}$ 是颗粒密度。
然而,人们观察到,在堵塞球体堆积中,低 $P$ 值时声速为 $V\propto P^{1/4}$,高 $P$ 值时声速为 $V\propto P^{1/6}$(我们将证明本研究中的实验仍处于 $V\propto P^{1/6}$ 阶段)。
这一观察结果可以通过颗粒在压缩条件下因滑动而屈服的接触____机制或非球形接触来解释。相反,正如声速测量所证明的那样,剪切加载可以减少接触的数量。
In the nonlinear acoustic regime, high amplitude sound waves can act as controlled perturbations to explore the glassy dynamics of a granular system. On the scale of the grain contacts, we distinguish two types of nonlinearity: one arises from the normal loading, i.e. Hertzian contact, and the other from the tangential friction force.
In the weakly nonlinear regime where the sound amplitude is much smaller than the grain overlap, reversible nonlinear responses, like second harmonic generation, are observed. Nevertheless, beyond a certain sound amplitude of only a few percent of the grain deformation, the sound-matter interactions become irreversible and are accompanied by slight compaction of magnitude $<0.1$ %.
Such a behavior is much more pronounced with low confining pressure $P$ in which strong fluctuations are observed both in the velocity and the amplitude of sound waves propagating through granular packings. This is likely related to the modification of the contact networks caused by the sound wave.
在非线性声学体系中,高振幅声波可以作为受控扰动来探索颗粒系统的玻璃化动力学。在颗粒接触的尺度上,我们区分了两种类型的非线性:一种来自法向载荷,即 Hertz 接触,另一种来自切向摩擦力。
在声振幅远小于颗粒重叠的弱非线性状态下,可观察到可逆的非线性反应,如二次谐波的产生。然而,超过一定的声振幅(仅为颗粒变形的百分之几),声-物质相互作用就变得不可逆,并伴随着幅度为 $<0.1$ % 的轻微压实。
However, some important issues still remain unclear such as the effect of the particle-level properties (shape and friction) on the structure and the mechanical responses of jammed granular packings. In this work, we aim to elucidate the role of the particle shape on the rigidity of a granular solid within the framework of effective medium theories based on the Hertzian–Mindlin contact law via the coordination number $Z$.
To this end, we develop a quantitative measurement of the phase velocity of longitudinal sound waves in the linear regime, and compare the pressure-dependent sound speed measured in the packings of glass beads and sand particles (Sect. 2). Next we investigate the evolution of a granular packing by the two following methods (Sect. 3): (i) repetitively applying a confining stress while measuring the sound speed; (ii) using nonlinear sound vibration to perturb the granular packing.
然而,一些重要问题仍不清楚,例如颗粒级特性(形状和摩擦力)对结构以及堵塞颗粒堆积的机械响应的影响。在这项研究中,我们的目标是在基于 Hertzian–Mindlin 接触定律的有效介质理论框架内,通过配位数 $Z$ 解释颗粒形状对颗粒固体刚性的作用。
为此,我们开发了线性(响应?)机制下纵波相速度的定量测量方法,并比较了在玻璃珠和沙粒堆积中测量到的随压力变化的声速(第 2 节)。接下来,我们用以下两种方法研究颗粒堆积的演变(第 3 节):(i) 在测量声速的同时重复施加约束应力;(ii) 使用非线性声振动来扰动颗粒堆积。
Coherent sound propagation in jammed packings
Experimental procedure
Our granular solids consist of random packing of spherical glass beads of diameter $d = 0.3\text{ mm}$ and $0.7\text{ mm}$ (made of soda lime glass) or sand particles of $d = 0.7\text{ mm}$ (made of $99$ % $\text{SiO}_{2}$). The densities of both materials are almost the same, about $2500\text{ kg/m}^3$. We measure the longitudinal sound speed through a single glass bead and a sand particle and find $5000$ and $5200\text{ m/s}$, respectively (measurement of the transverse sound speed is not possible due to echos and reverberation).
我们的颗粒状固体由直径为 $d = 0.3\text{ mm}$ 和 $0.7\text{ mm}$ (由钠钙玻璃制成)的球形玻璃珠或直径为 $d = 0.7\text{ mm}$ (由 $99$ % $\text{SiO}_{2}$ 制成)的沙粒随机堆积而成。这两种材料的密度几乎相同,约为 $2500\text{ kg/m}^3$。我们测量了穿过单个玻璃珠和沙粒的纵波声速,结果分别为 $5000$ 和 $5200\text{ m/s}$ (由于回声和混响,无法测量横波声速)。
These data show a slight difference of $<5$ % in elastic modulus. Glass beads and sand particles are poured via rain deposition into a rigid cylindrical cell with an inner diameter of $D = 60\text{ mm}$. After the cell is filled up to a height $x$ (varying from $9$ to $18\text{ mm}$), the confined granular packing is consolidated by applying ten-cycles of axial loading and unloading, via the upper piston, up to a pressure $P$ (ranging from $0.03$ to $1\text{ MPa}$) at which the acoustic measurements are conducted (Fig. 1).
这些数据显示,弹性模量的差异略微小于 $5$%。玻璃珠和沙粒通过雨落法倒入内径为 $D = 60\text{ mm}$ 的刚性圆柱形池中。在小室被填充到一个高度 $x$(从 $9$ 到 $18\text{ mm}$ 不等)之后,通过上部活塞施加十个周期的轴向加载和卸载,将密闭的颗粒堆积加载到应力 $P$(从 $0.03$ 到 $1\text{ MPa}$ 不等),在此压力下进行声学测量(图 1)。
The packing density of these granular materials is $\phi\approx 0.63$ for glass beads and $\phi\approx 0.59$ for sand particles. For generating and detecting the longitudinal sound waves in the granular sample, we use broadband piezoelectric transducers of $30\text{ mm}$ diameter which are placed in direct contact with the granular packing. In these experiments, the excitation is performed by sending one-cycle short pulse of $2\mu\text{s}$ duration with a broadband spectrum centered at $500\text{ kHz}$.
这些颗粒材料的堆积密度为:玻璃珠约为 $0.63$,沙粒约为 $0.59$。为了产生和探测颗粒样本中的纵向声波,我们使用了直径为 $30 \text{ mm}$ 的宽带压电换能器,该换能器与颗粒堆积直接接触。在这些实验中,激励是通过发送持续时间为 $2\mu\text{s}$ 的单周期短脉冲来实现的,其宽带频谱的中心为 $500\text{ kHz}$。
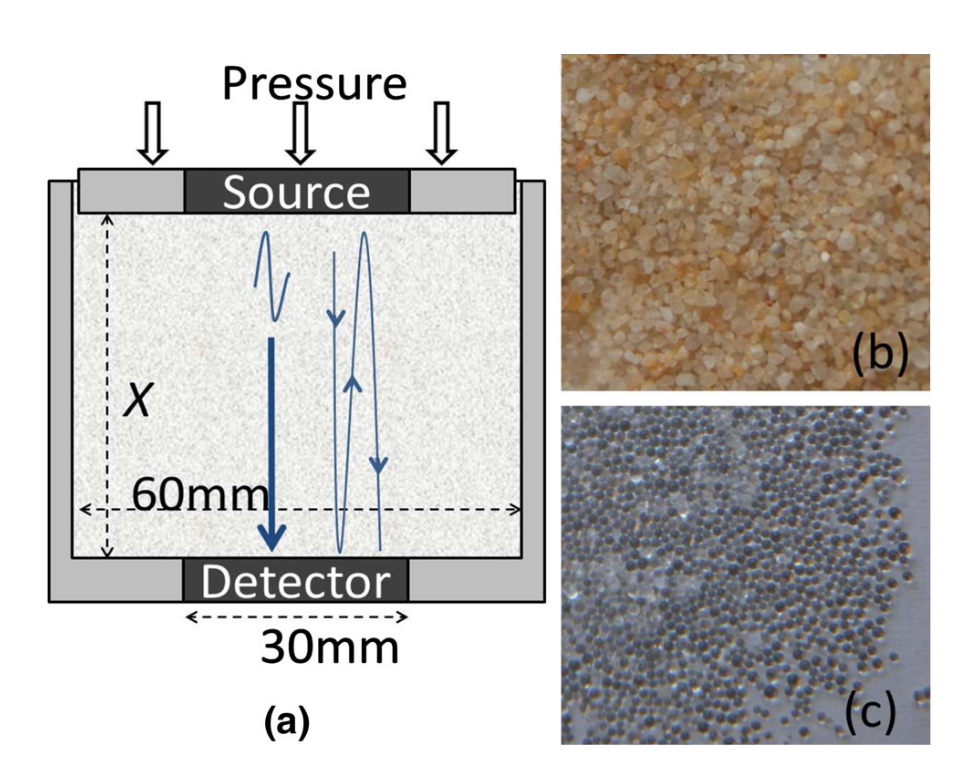
Schematic of the setup used in the linear sound experiments. a Glass beads are contained in a metal cell and a pressure is applied via a piston. A transducer placed in the piston serves as acoustic source by sending a $2\mu\text{s}$ pulse and the propagating wave is measured by a second transducer placed at the bottom of the cell. An echo is indicated by the curved arrow. b Photo of the sand particles $d$
$0.7\text{ mm}$. c Photo of the glass beads $d$$0.7\text{ mm}$.线性声实验中使用的装置示意图。a 玻璃珠装在一个金属池中,通过活塞施加压力。放置在活塞中的换能器通过发送 $2\mu\text{s}$ 脉冲作为声源,传播波由放置在颗粒池底部的第二个传感器测量。曲线箭头表示回声。b 沙粒的照片 $d$
$0.7\text{mm}$。c 玻璃珠的照片 $d$$0.7\text{毫米}$。
Typical short sound pulses (broadband) propagating through a glass bead packing of $d = 0.4\text{ mm}$ for a sample thickness $x_{1} = 9\text{ mm}$ and $x_{2} = 18\text{ mm}$ are shown in Fig. 2. The experiments are repeated for different confining pressures $P$ to study the evolution of the sound speed (see below).
As shown previously in [11], the use of large acoustic source and receiver enhance the detection of the long-wavelength coherent sound waves and minimize the codalike acoustic speckles. Indeed, we clearly recognize the round-trip echo of the longitudinal sound wave even though it is strongly damped by the scattering attenuation.
Note also that, with this protocol and confining pressure $P$, the coherent acoustic pulses are reproducible with fluctuations $<5$ % in amplitude and $3$ % in time-of-flight between different configuration (ten different configurations).These observations confirm the applicability of the effective medium theory (EMT) or mean-field approach to describe a jammed granular solid on the macroscopic scale, corresponding to the coherent wavelength $\lambda\sim 5\text{ mm}$ ($>d\sim 0.5\text{ mm}$).
典型的短声脉冲(宽带)在样品厚度为 $x_{1} = 9\text{ mm}$ 和 $x_{2} = 18\text{ mm}$的 $d = 0.4\text{ mm}$ 玻璃珠堆积中传播,如图 2 所示。针对不同的约束压力 $P$ 重复实验,以研究声速的演变(见下文)。
如之前的文献[11]所示,使用大型声源和接收器可增强对长波长相干声波的探测,并最大限度地减少多重散射声学散乱峰。事实上,尽管纵向声波受到散射衰减的强烈阻尼效应,我们仍能清晰地识别出纵向声波的回响。
还要注意的是,采用这种方案和约束压力 $P$,相干声脉冲在不同配置($10$ 种不同配置)之间的振幅波动 $<5$ % 和飞行时间波动 $3$ %,具有可重复性。这些观察结果证实了有效介质理论(EMT)或均场方法适用于描述宏观尺度上的堵塞态颗粒固体,相当于相干波长 $\lambda\sim 5\text{ mm}$ ($>d\sim 0.5\text{mm}$)。
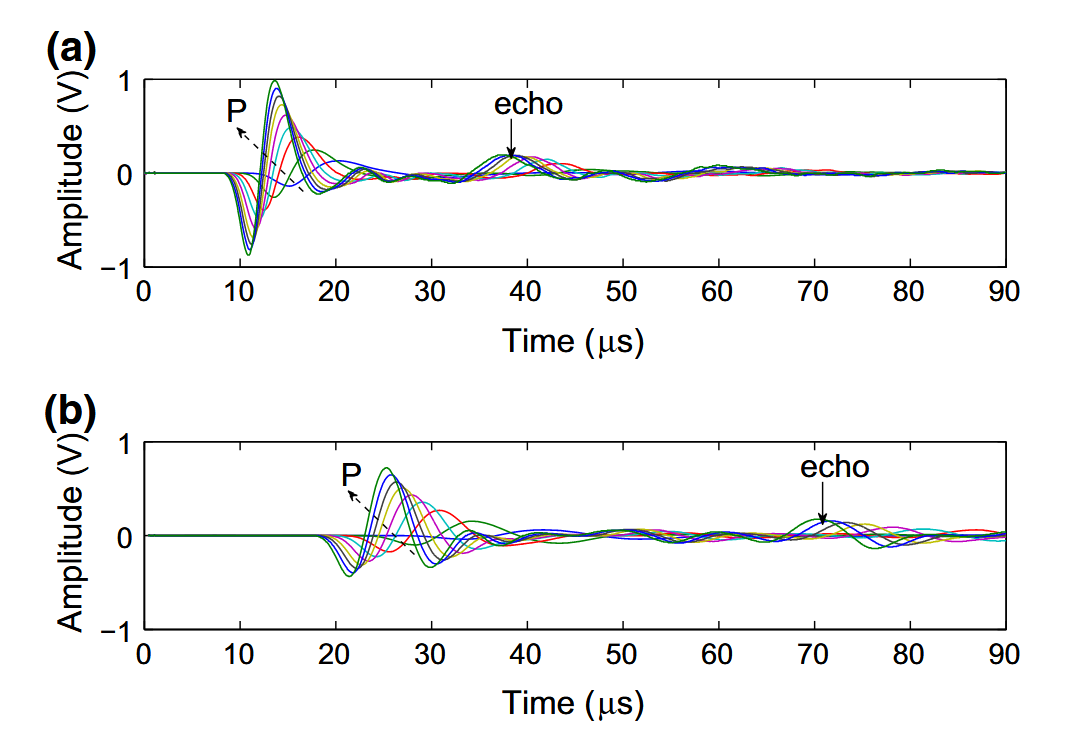
Measured sound signals propagating in granular samples consisting of glass beads, $d = 0.4\text{ mm}$, for increasing confining pressures [indicated by the dotted arrows, 35, 88, 177, 265, 354, 442, 530, 618, 707 kPa (color online)] at distance $x_{1} = 9{\text{ mm}}$ (a), and $x_{2} = 18{\text{ mm}}$ (b). The small solid arrows indicate the echo’s
在距离 $x_{1} = 9{\text{ mm}}$(a)和 $x_{2} = 18{\text{ mm}}$(b)处,测量到的声音信号在由玻璃珠组成的颗粒样品($d = 0.4\text{毫米}$)中传播[虚线箭头表示$35,88,177,265,354,442,530,618,707\text{ kPa}$(彩色在线)]。实心小箭头表示回波
Sound speed measurement
To accurately measure the wave speed of the coherent sound propagation, we determine the time delay between two coherent longitudinal sound pulses measured at different distances from the acoustic source, $x_1 = 9\text{ mm}$ (Fig. 2a) and $x_2 = 18\text{ mm}$ (Fig. 2b). As the temporal waveforms of sound pulses are significantly changed as a function of propagation distance $x$, we seek to determine the phase velocity by the spectral analysis of such broadband sound pulses through the granular packing at a given pressure $P$.
Indeed, if one considers a plane wave of angular frequency $\omega$, $s(x, t) = A_{0}e^{-\alpha x}e^{i(\omega x/V_{\varphi} - \omega t)}$ where $\alpha(\omega)$ is the attenuation and $V_{\varphi}(\omega)$ is the phase velocity.
These two parameters can be determined from the ratio of magnitude $S(\omega, x) = A_{0}e^{-\alpha x}$ and the difference of phase $\phi(\omega, x) = \omega x/V_{\varphi}$ measured at two different distances of propagation separated by $\Delta x = x_{2} − x_{1}$,
$$ \alpha = \ln{\frac{S_{1}}{S_{2}}}/\Delta x\\ V_{\varphi} = \omega\frac{\Delta x}{\Delta\varphi} $$
为了精确测量相干声传播的波速,我们测定了在距离声源不同距离测量的两个相干纵向声脉冲之间的时间延迟,分别为 $x_1 = 9\text{ mm}$(图 2a)和 $x_2 = 18\text{ mm}$(图 2b)。由于声脉冲的时间波形随传播距离 $x$ 的变化而显著改变,我们试图通过对在给定压力 $P$ 下穿过颗粒堆积的宽带声脉冲进行频谱分析来确定相位速度。
事实上,如果考虑角频率为 $\omega$ 的平面波,$s(x, t) = A_{0}e^{-\alpha x}e^{i(\omega x/V_{\varphi} - \omega t)}$ 其中 $\alpha(\omega)$ 是衰减,$V_{\varphi}(\omega)$ 是相速度。
这两个参数可以通过在两个不同的传播距离上测量的幅度比 $S(\omega, x) = A_{0}e^{-\alpha x}$ 和相位差 $\phi(\omega, x) = \omega x/V_{\varphi}$ 来确定,这两个距离相隔 $\Delta x = x_{2}- x_{1}$,
$$ \alpha = \ln{\frac{S_{1}}{S_{2}}}/\Delta x\\ V_{\varphi} = \omega\frac{\Delta x}{\Delta\varphi} $$
The magnitude spectra (Fig. 3a, b) of the sound pulses measured at $x_1$ and $x_2$ are obtained by the Fourier transformation after the application of a window function to separate the coherent longitudinal wave from the shear wave and also from the codalike scattered waves. These magnitude spectra show that the central frequency of the transmitted sound pulse increases with increasing pressure and it decreases with increasing distance of propagation due to the scattering attenuation of the coherent wave, indicating that the granular medium acts as a low-pass filter. The phase velocity is determined with Eq. (4) using the phase spectra (not shown), as a function of frequency for different confining pressure (Fig. 3c).
在应用窗函数将相干纵波与剪切波以及同类散射波分离后,通过傅里叶变换获得了在 $x_1$ 和 $x_2$ 处测量的声脉冲的幅值频谱(图 3a、b)。这些幅值谱显示,由于相干波的散射衰减,透射声脉冲的中心频率随压力的增加而增加,并随传播距离的增加而减小,这表明颗粒介质起到了低通滤波器的作用。根据公式 (4),利用相位频谱(未显示)确定了相位速度,它是不同约束压力下频率的函数(图 3c)。
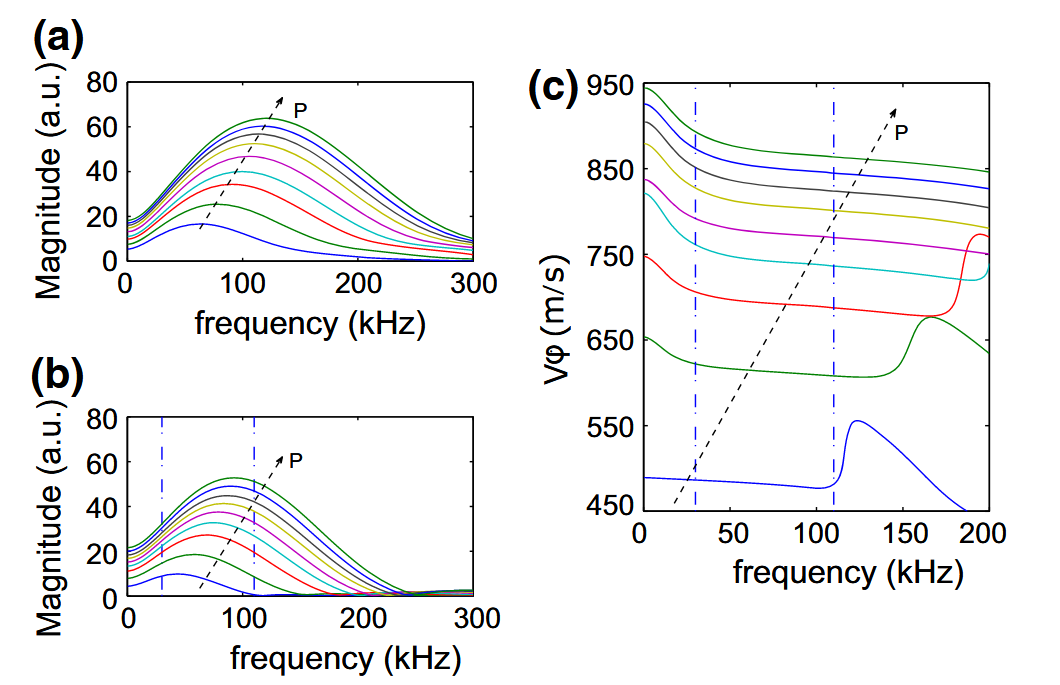
Spectra calculated from the coherent part of the wave in Fig. 2 at distance a $x1 = 9\text{ mm}$, and b $x2 = 18\text{ mm}$. c Phase velocity of the coherent wave, $V_{\varphi}$, as a function of the frequency. The dashed arrows indicate the increasing confining pressure; $35, 88, 177, 265, 354, 442, 530, 618, 707$(color online). The vertical blue dotted lines indicate the available frequency range in which we perform our sound speed measurements
图 2 中相干波部分在距离 a $x1 = 9\text{ mm}$ 和 b $x2 = 18\text{ mm}$ 时的频谱计算结果。c 相干波的相速度 $V_{\varphi}$ 是频率的函数。虚线箭头表示不断增加的约束压力;$35, 88, 177, 265, 354, 442, 530, 618, 707$(彩色在线)。垂直蓝色虚线表示我们进行声速测量的可用频率范围
Within the available range of frequency (from $10$ to $100\text{ kHz}$) obtained for different pressure, the measured phase velocity decreases slightly with increasing the frequency, indicating a small dispersion effect (the structures appearing outside the available frequency range are likely due to experimental limitations and should not be interpreted). This dispersion effect is not predicted by the existing effective medium theories. However, other models suggest possible dispersion effects related to the characteristic size of the particles in disordered amorphous systems. Further studies are needed to clarify this issue.
在不同压力下获得的可用频率范围内(从 $10$ 到 $100\text{ kHz}$),测量到的相速度随着频率的增加而略有下降,这表明存在微小的色散效应(出现在可用频率范围之外的结构可能是由于实验限制造成的,不应加以解释)。现有的有效介质理论无法预测这种色散效应。不过,其他模型表明,可能的频散效应与无序无定形系统中颗粒的特征尺寸有关。要澄清这个问题,还需要进一步的研究。
In Fig. 4, we plot the averaged phase velocity of longitudinal sound waves $V_{\varphi}$ as a function of confining pressure $P$ obtained in the jammed packings of glass beads and irregular/angular sand particles. Note that these data agree well ($1 \%$) with the group velocity $V_{g}$ (Fig. 4c, inset) determined at a given $P$, using the correlation method (i.e., the group delay) between the sound pulses detected at $x_{1}$ and $x_{2}$ (Fig. 2).
在图 4 中,我们绘制了在玻璃珠和不规则/方形沙粒的卡压堆积中获得的纵波平均相速度 $V_{\varphi}$ 与约束压力 $P$ 的函数关系。请注意,这些数据与利用在 $x_{1}$ 和 $x_{2}$(图 2)处检测到的声脉冲之间的相关方法(即群延迟)确定的给定 $P$ 下的群速度 $V_{g}$(图 4c,插图)非常吻合(1 \%$)。
We observe an increase of the sound speed with increasing confining pressure, in both glass beads and sand packings. This increase is qualitatively captured by the effective medium model based on the hertzian contact shown in Eqs. (1) and (2). Furthermore, we observe that the size of the glass beads does not effect the sound speed. In contrast, we find that the sound speeds measured in sand particle packings are significantly lower than (about $20 \%$) those in glass beads packings, no matter what the confining pressure is.
我们观察到,在玻璃珠和砂堆积中,声速随着约束压力的增加而增加。公式 (1) 和 (2) 所示的基于 Hertzian 接触的有效介质模型定性地察觉到了这一增长。此外,我们观察到玻璃珠的大小并不影响声速。相反,我们发现无论约束压力如何,在沙粒堆积中测得的声速都明显低于玻璃珠堆积中测得的声速(约 $20 \%$)。
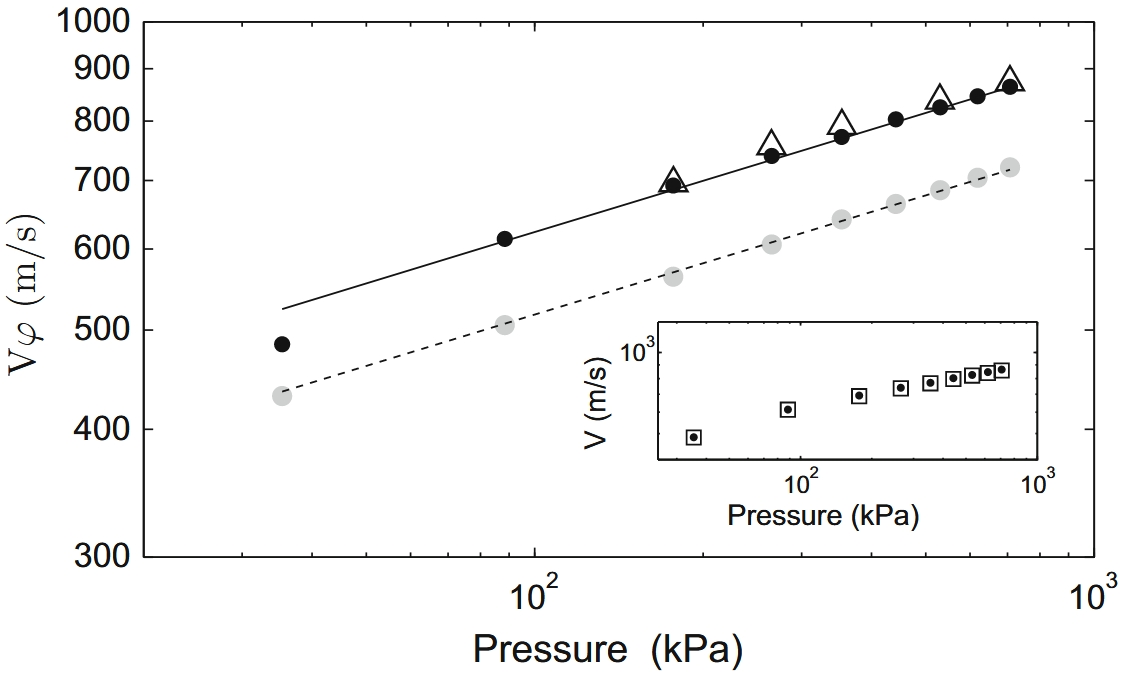
Phase velocity, $V_{\varphi}$, of the propagating sound as a function of confining pressure $P$ for of glass beads ($d = 0.4\text{ mm}$ in black dots and $d = 0.7\text{ mm}$ in open triangles) and sand ($d = 0.77\text{ mm}$ in grey dots). The lines indicate fits of the EMT (see text), with the only free fitting parameter $Z = 6.3$ for glass (line) and $Z = 3.9$ for sand (dashed line). The error bar is estimated to be $2 \%$ and is equal to the symbol size. The dashed arrows indicate the increasing confining pressure. The inset shows agreement between the group velocity (open squares) and the phase velocity (black dots) measured in glass beads $d = 0.4\text{ mm}$
玻璃珠( $\cdot$ 为 $d = 0.4\text{ mm}$,$\Delta$ 为 $d = 0.7\text{ mm}$)和沙子(灰点为 $d = 0.77\text{ mm}$)的传播声相位速度 $V_{\varphi}$,作为约束压力 $P$ 的函数。线条表示 EMT 的拟合(见正文),玻璃(直线)的唯一自由拟合参数为 $Z = 6.3$,沙子(虚线)的唯一自由拟合参数为 $Z = 3.9$。误差条估计为 $2\%$,等于符号大小。虚线箭头表示不断增加的约束压力。插图显示了在玻璃珠 $d = 0.4\text{ mm}$ 中测得的群速度($\square$)与相速度($\cdot$)之间的一致性。
A few remarks may be made here on these interesting results. First, in the limited range of confining pressures, our experiments on sand packings can be described by an EMT based a Hertzian-like spherical contact law. This is surprising since the non-Hertzian contacts may lead to a different scaling of the contact stiffness and the confining pressure. Indeed a point-side contact results in a contact stiffness of $k\propto P^{1/2}$ (for a hertzian contact, $k\propto P^{1/3}$) whereas the stiffness of a side-side may be independent on the pressure. Our result could be due to the averaging over all the possible contact configurations that are available for angular particles.
在此,我们可以就这些有趣的结果谈几点看法。首先,在有限的约束压力范围内,我们对砂堆积的实验可以用基于类似 Hertzian 球形接触定律的 EMT 来描述。这是令人惊讶的,因为非 Hertzian 接触可能会导致接触刚度和约束压力的不同比例。事实上,点-侧接触会导致接触刚度为 $k\propto P^{1/2}$(对于 Hertzian 接触,为 $k\propto P^{1/3}$),而侧接触的刚度可能与压力无关。我们的结果可能是由于对含角粒子所有可能的接触构型进行了平均。
Therefore, the non-spherical contact law cannot alone account for the large difference ($\sim 20\%$) in the sound speed between glass bead and sand particle packings. Second, because of the similar values of the density and elastic modulus for glass and sand materials, confirmed by the longitudinal sound speed measurement (Sect. 2.1), the material difference can also not account for the large difference in the sound velocity between glass and sand packings.
Considering these two remarks, we suggest that the significant lower sound velocity in sand packings compared to glass bead packings is primarily related to the angularity of the sand particles, which allows a stable packing at small contact number for a stable packing (see Sect. 4).
因此,非球类接触定律不能单独解释玻璃珠和沙粒堆积之间声速的巨大差异($\sim 20%$)。其次,由于纵向声速测量(第 2.1 节)证实玻璃和砂材料的密度和弹性模量值相似,因此材料差异也不能解释玻璃和砂堆积之间声速的巨大差异。
考虑到这两点,我们认为与玻璃珠堆积相比,砂堆积的声速明显较低,这主要与砂粒的角性有关,砂粒的角性可以使堆积在小接触数下形成稳定的堆积(见第 4 节)。
Probing the contact change in granular packings
Response to cyclic loading–unloading
To characterize the relationship between the particle shape (or surface friction) and the mechanical properties of jammed granular packings, we developed an experimental protocol in which an axial stress ($177\text{ kPa}$) was repetitively applied to a granular sample. This cyclic loading-unloading induces the significant particle motion leading to the compaction of the granular sample.
为了确定颗粒形状(或表面摩擦力)与堵塞颗粒堆积的机械特性之间的关系,我们开发了一种实验方案,即在颗粒样品上重复施加轴向应力($177\text{ kPa}$)。这种循环加载-卸载诱导了颗粒的显著运动,从而导致颗粒样品的压实。
To monitor both changes in the packing density and the effective stiffness under cyclic loading, we precisely measured the evolution of the sample height $x$, the sound speed $V$ and the peak-to-peak amplitude ($U$) of short-pulse sound transmission (Fig. 2). Note that for probing the sound speed change, we adopted a simple protocol to monitor the evolution of the time-of-flight associated with the pulse peak. The experiments were performed on both dry and wet packings consisting of glass beads or sand particles; each experiment was repeated $n = 5$ times.
为了监测循环加载下堆积密度和有效刚度的变化,我们精确测量了样品高度 $x$、声速 $V$ 和短脉冲声音传输的峰-峰振幅 ($U$) 的变化(图 2)。需要注意的是,在探测声速变化时,我们采用了一个简单的方案来监测与脉冲峰值相关的飞行时间的演变。实验在由玻璃珠或沙粒组成的干堆积和湿堆积上进行,每次实验重复 $n = 5$。
Typical results obtained in dry packings of glass beads $d = 1.5\text{ mm}$ and sand particles $d = 1.8\text{ mm}$ are shown in Fig. 5. For glass bead packings, the sample height after the first loading cycle is $x\simeq 4\text{ cm}$. For all the experiments ($n = 5$), we observe a typical compaction of $1–2\%$ after $150$ loading cycles (Fig. 5a). During this compaction, the sound amplitude shows a prominent increase ($3–4$ times increase) (Fig. 5b) while the sound speed increases about $2–5\%$ (Fig. 5c).
图 5 中显示了玻璃珠 $d = 1.5\text{ mm}$ 和沙粒 $d = 1.8\text{ mm}$ 干燥堆积的典型结果。对于玻璃珠堆积,第一次加载循环后的样品高度为 $x\simeq 4\text{ cm}$。在所有实验中($n = 5$),我们观察到在 $150$ 加载周期后,典型的压实度为 $1-2\%$ (图 5a)。在这种压实过程中,声振幅显示出明显的增加(增加 $3-4$ 倍)(图 5b),而声速增加约 $2-5\%$ (图 5c)。
The obtained results in sand particle packings are similar to those found in glass beads, i.e, (i) a granular compaction of about $1–2\%$ despite the difference between the initial packing densities; and, (ii), an increase in sound amplitude during compaction. However, the absolute value of the sound amplitude was much lower in sand particle than in glass bead packings. Moreover, the sound speed appeared to be constant independent of the compaction.
在砂粒堆积中获得的结果与玻璃珠堆积中的结果相似,即:(i) 尽管初始堆积密度不同,但颗粒压实度约为 $1–2\%$; (ii) 在压实过程中声振幅增大。然而,沙粒的声振幅绝对值比玻璃珠堆积的声振幅绝对值低得多。此外,声速似乎与压实无关。
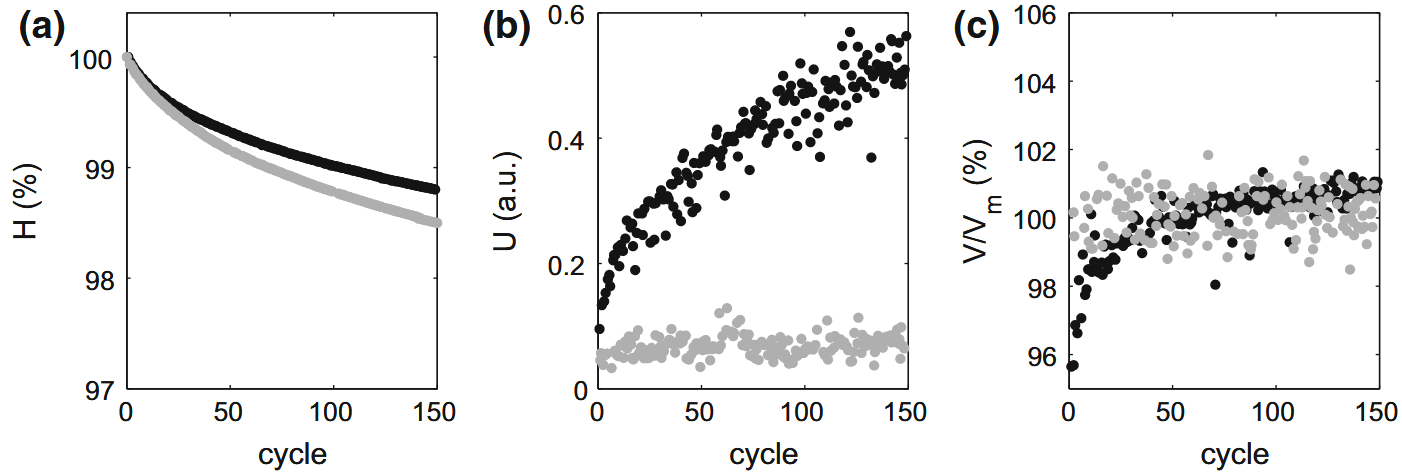
Typical traces showing the evolution of dry packings of glass beads (black) and sand particles (grey) under cyclic loading. a Sample height normalized by the particle diameter versus the number of cycles. b Sound amplitude versus the number of cycles. c Sound speed divided by the average sound speed, $V_{m}$ , versus the number of cycles
显示玻璃珠(黑色)和沙粒(灰色)在循环加载下干堆积演变的典型轨迹。 a 以颗粒直径归一化的样品高度与循环次数的关系。 b 声幅与周期数的关系。 c 声速除以平均声速 $V_{m}$ 与循环次数的关系
We next investigated the response of wet granular packings to cyclic loading (Fig. 6). Adding a small amount of silicon-oil ($1\%$ volume fraction) to the granular sample allows the formation of a liquid film at the contact between particles; it changes the surface friction and adhesion at solid particle contacts and increases the sound absorption. Experiments on wet packings of glass beads and sand particles reveal three main features (Fig. 6). First, the compaction of wet packings was comparable to the compaction of dry packings under cyclic loading.
我们接下来研究了湿颗粒堆积对循环加载的响应(图 6)。在颗粒样品中加入少量硅油(体积分数为 $1\%$)可以在颗粒之间的接触处形成一层液膜;它可以改变固体颗粒接触处的表面摩擦力和附着力,并增加吸音效果。玻璃珠和沙粒的湿堆积实验揭示了三个主要特征(图 6)。首先,在循环加载下,湿堆积的压实度与干堆积的压实度相当。
Second, the evolution of the sound speed $V$ on the compaction was lowered by the presence of oil. Indeed, while the sound velocity in dry glass bead packings showed a clear increase, the sound speed in wet glass bead packing remained almost constant during the compaction. The absolute value of the transmitted sound amplitude was also slightly reduced in wet packings. These results show that the dynamics of the grain-grain contacts under stress induced by the cyclic loading was altered by the presence of oil.
其次,油的存在降低了声速 $V$ 在压实过程中的变化。事实上,干玻璃珠堆积中的声速明显增加,而湿玻璃珠堆积中的声速在压实过程中几乎保持不变。在湿堆积中,透射声振幅的绝对值也略有降低。这些结果表明,在循环加载引起的应力作用下,颗粒与颗粒之间的接触动力学因油的存在而发生了改变。
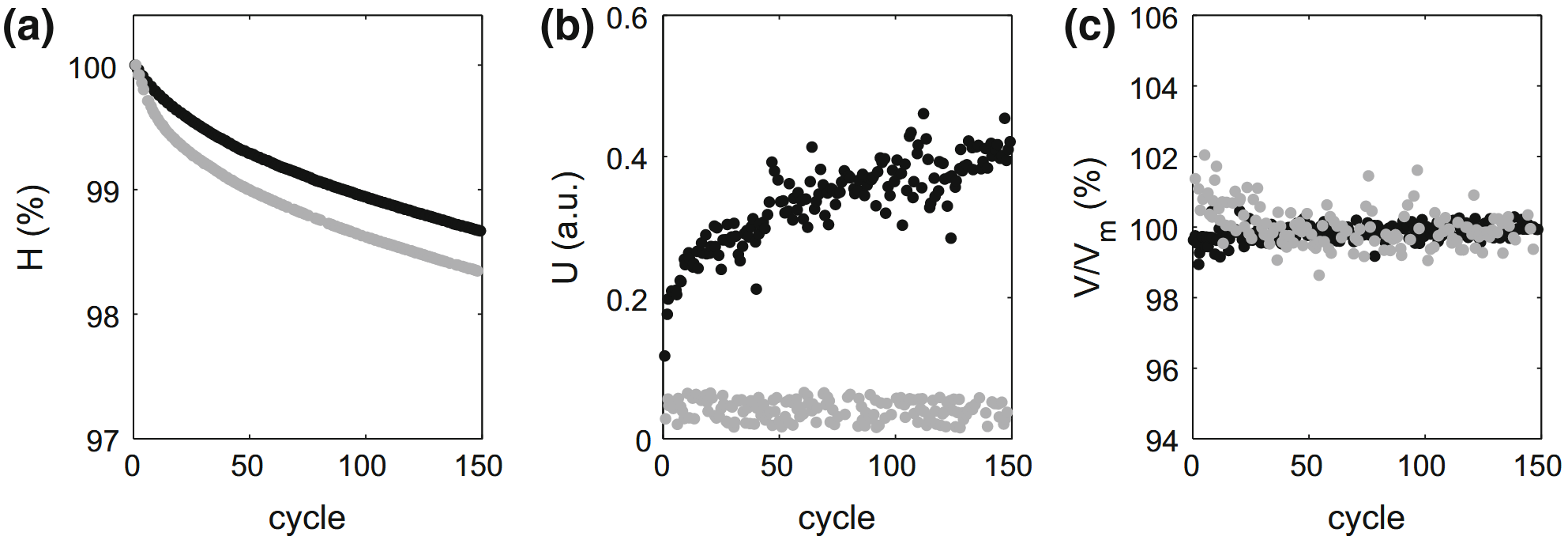
Typical traces showing the evolution of wet packings of glass beads (black) and sand particles (grey) under cyclic loading. a Sample height normalized by the particle diameter versus the number of cycles. b Sound amplitude versus the number of cycles. c Sound speed divided by the average sound speed, $V_{m}$ , versus the number of cycles
显示玻璃珠(黑色)和沙粒(灰色)的湿堆积在循环加载下演变的典型轨迹。 a 以颗粒直径归一化的样品高度与循环次数的关系。 b 声幅与周期数的关系。 c 声速除以平均声速 $V_{m}$ 与周期数的关系
In contrast, the effect of the presence of oil on the sound amplitude is limited, confirming that the attenuation of the coherent waves is dominated by sound scattering as mentioned above. Since the driving amplitude is the same for the sound amplitude transmitted in glass bead and sand particle packings, the clear difference measured in Figs. 5b and 6b may be due to a larger scattering attenuation in the sandpile because of a looser packing or a more sparse contact network.
相比之下,油的存在对声幅的影响有限,这证明相干波的衰减主要是由上述的声散射造成的。由于玻璃珠和沙粒堆积中传播的声幅的驱动振幅相同,图 5b 和图 6b 中测得的明显差异可能是由于沙堆中的堆积更松散或接触网络更稀疏,导致散射衰减更大。
Response to nonlinear acoustic vibration
Finally, we investigated the evolution of a sand particle packing subjected to high-amplitude sound transmission in the course of time (longer than one hour). The experiments are preformed in a setup where the transducers are $10\text{ cm}$ under the surface of the sand and the pressure in the packing is only due to gravity, corresponding to a $P\sim 2\text{ kPa}$ (Fig. 7a).
最后,我们研究了沙粒堆积在高振幅声波传播过程中(超过一小时)的演变情况。实验是在换能器位于沙表面下 $10$ 厘米处进行的,堆积中的压力仅由重力造成,相当于 $P\sim 2\text{ kPa}$(图 7a)。
The input amplitude $U_{i}$ of the excitation pulse is ramped up-down (Fig. 7b). We use narrow band Gaussian-like ten-pulses centered at $8\text{ kHz}$ (Fig. 7c) and we monitor the change in the group velocity $V_{g}$ of the longitudinal sound pulses as a function of time (for more details on the experimental protocol see [24]).
激励脉冲的输入振幅 $U_{i}$ 是上下起伏的(图 7b)。我们使用以 $8\text{ kHz}$ 为中心的窄带高斯样十脉冲(图 7c),并监测纵向声脉冲的群速度 $V_{g}$ 随时间的变化(有关实验方案的更多详情,请参阅 [24])。
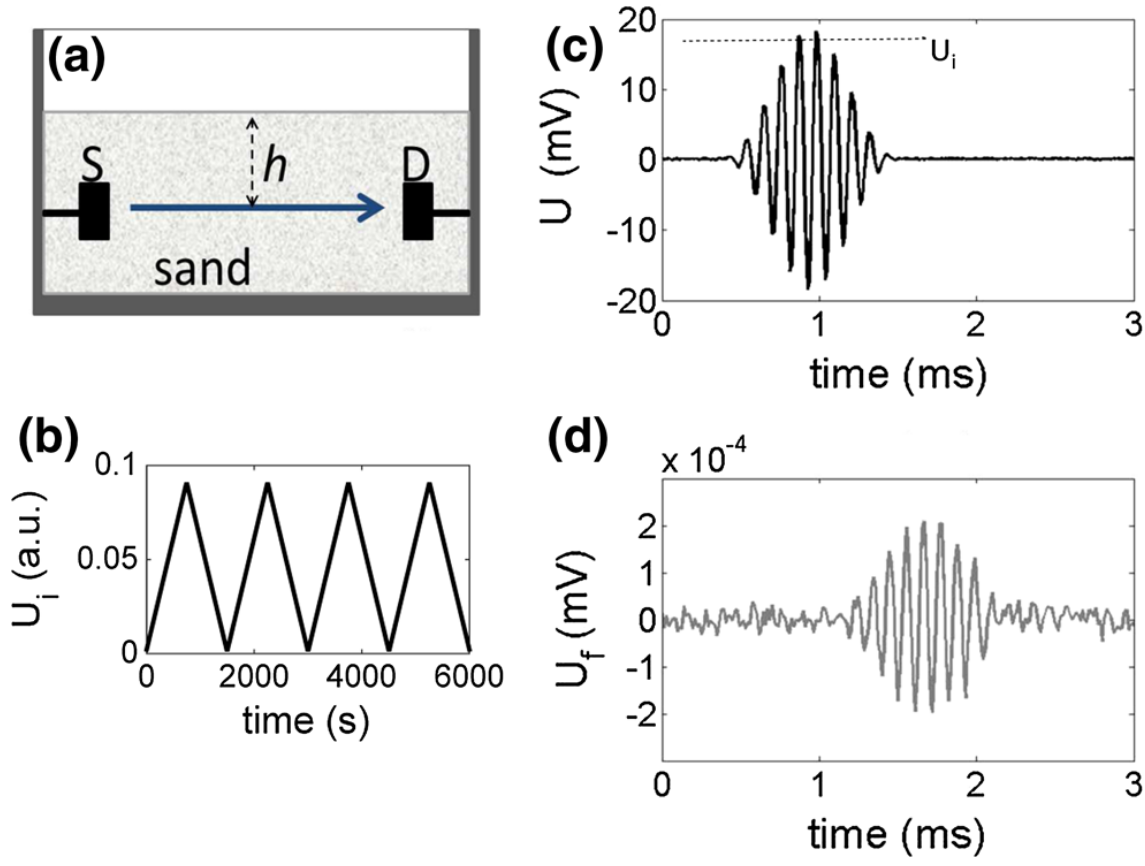
Set-up of nonlinear sound measurements. a Sand is contained in a plexiglas cell and the pressure is regulated by the fill height $h$ to be about $10\text{ cm}$ and $S$ is the source transducer, $D$ the detector transducer. b The amplitude of excitation $U_{i}$ was ramped up and down. c Excitation sound pulse. The dotted line indicates the input amplitude of the excitation sound pulse, $U_{i}$. d Sound signal measured in sand
准备非线性声音测量。 a 有机玻璃池中装有沙子,压力由填充高度 $h$ 调节,约为 $10\text{cm}$,$S$ 为源换能器,$D$ 为检测器换能器。 b 激发振动波幅 $U_{i}$ 上下起伏。 c 激发声脉冲。虚线表示激励声脉冲的输入振幅 $U_{i}$。 d 在沙中测量的声音信号
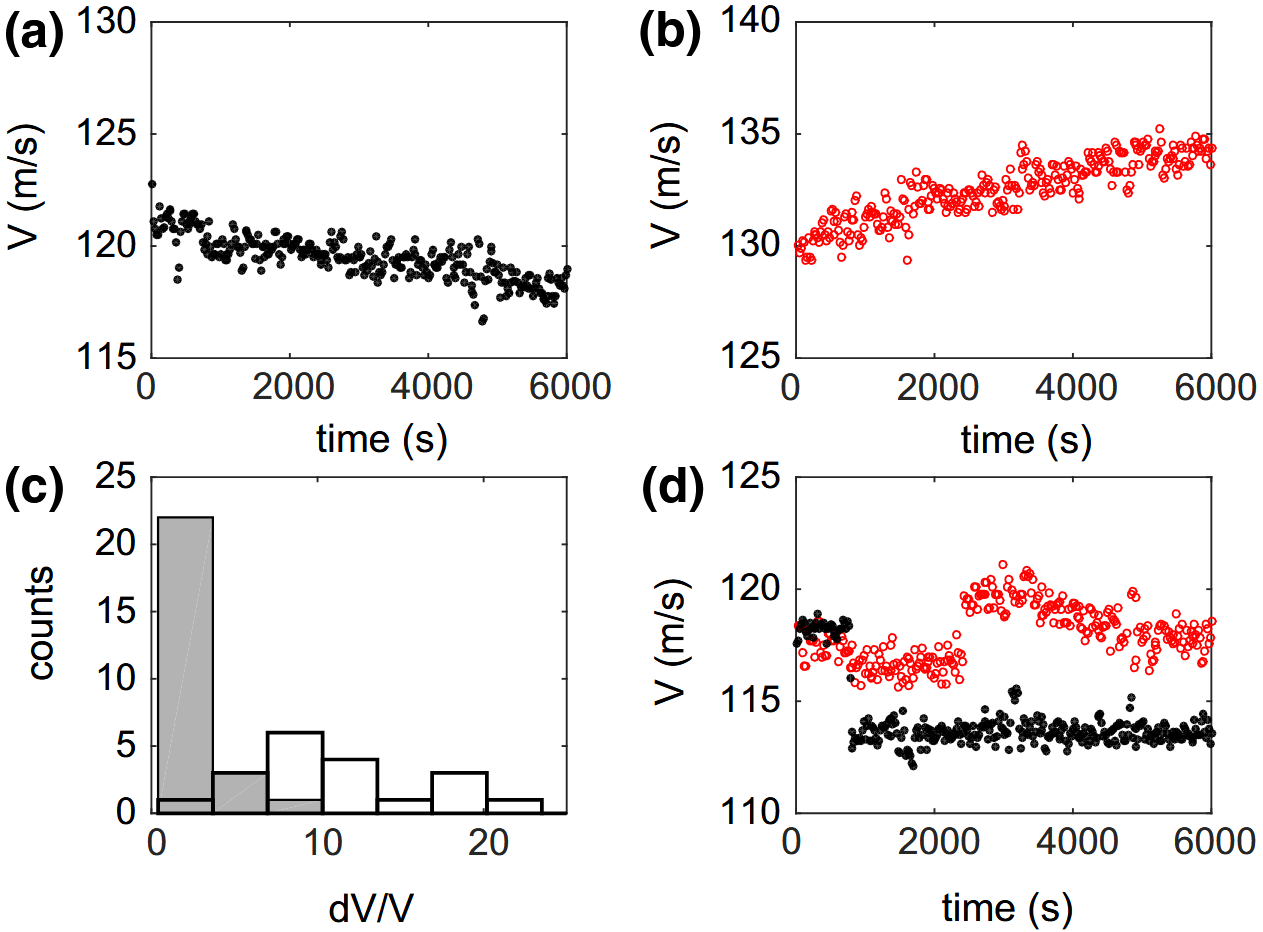
A typical sound signal measured in sand packings is shown in Fig. 7d. As previously reported for glass bead packings, we find again in sand particle packings two distinct nonlinear acoustic responses, namely, (i) a weakening in which the sound speed decreases as a function of time (Fig. 8a) and (ii) a strengthening evidenced by the increase of the sound speed (Fig. 8b), without the detection of significant change in the packing density $\phi$. Note, that whether a packing of sand strengthens or weakens is not only controlled by the sound amplitude of excitation, but it also depends on the history (e.g., sample preparation) and particular microstate of the granular packing itself.
在砂堆积中测量到的典型声音信号如图 7d 所示。与之前报告的玻璃珠堆积一样,我们在砂粒堆积中再次发现了两种截然不同的非线性声学响应,即:(i) 声速随时间变化而减弱(图 8a)和(ii) 声速随时间变化而增大(图 8b),但没有检测到堆积密度 $\phi$ 的显著变化。需要注意的是,砂堆积的增强或减弱不仅受激发声幅的控制,还取决于颗粒堆积本身的历史(如样品制备)和特定的微观状态。
Nonlinear sound induces fluctuations of the sound speed in packings of sand particles. a A decrease of the sound speed. b A increase of the sound speed. c The fluctuation in the sound speed in sand particles are quantified (filled bins) and for comparison the data from [24] is added (bold outlined bins). d Abrupt decrease (black symbols) and increase (open red symbols) in the sound speed in brittle sand packings
非线性声波会引起沙粒堆积中的声速波动。 a 音速降低。 b 音速增加。 c 沙粒中的声速波动被量化(实心标记),为便于比较,添加了 [24] 的数据(粗体勾线箱)。 d 脆性砂堆积中声速的骤减(黑色符号)和骤增(空心红色符号)
We noticed that the change in sound speed over time in sand particle packings appears to be significantly lower than those observed in glass bead packings. To confirm this, we calculated the variation in sound speed over time for all the experiments in which we observed a gradual strengthening or weakening in sand particle packings.
我们注意到,砂粒堆积的声速随时间的变化似乎明显低于玻璃珠堆积。为了证实这一点,我们计算了观察到沙粒堆积逐渐增强或减弱的所有实验中声速随时间的变化。
As a comparison, we performed similar calculations on the data of our previous work on glass bead packings. The resulting histogram (Fig. 8c) indicates that the change in sound speed measured in sand particle packings ($3\%$) is clearly less important than the change previously measured in glass bead packings ($10\%$). This shows that the particle shape plays an important role in the evolution of a granular medium to external vibration.
作为比较,我们对以前关于玻璃珠堆积的工作数据进行了类似的计算。结果直方图(图 8c)表明,在沙粒堆积中测得的声速变化($3\%$)显然没有之前在玻璃珠堆积中测得的声速变化($10\%$)重要。这表明,颗粒形状在颗粒介质对外部振动的演变中起着重要作用。
Additionally, we find a new behavior in sand particle packings that we did not observe before in glass bead packings: there is occasionally an abrupt decrease or increase in the measured sound velocity (Fig. 8d) and amplitude (not shown). This change is typically of the order of a few percent of the sound velocity and may happen either in the weakening or in the strengthening. We believe that sound vibration may reduce the microscopic surface friction which dominates in the glass bead packing, causing slow and continuous change. Instead, for the sand packing, geometrical (macroscopic) friction is dominant, due to particle shape, and the change in the microstructure would be much more brittle.
此外,我们还在砂粒堆积中发现了一种新的行为,这是我们以前在玻璃珠堆积中没有观察到的:测得的声速(图 8d)和振幅(未显示)偶尔会突然降低或升高。这种变化通常为声速的百分之几,可能发生在减弱过程中,也可能发生在增强过程中。我们认为,声音振动可能会减少玻璃珠堆积中占主导地位的微观表面摩擦,从而导致缓慢而持续的变化。相反,对于砂堆积来说,由于颗粒形状的原因,几何(宏观)摩擦力占主导地位,微观结构的变化会更脆。
Discussion
In this study we investigate the influence of the particle shape on the mechanical properties of the granular material by using both linear and nonlinear coherent sound propagation. We seek to interpret these observations within the framework of the effective medium theory, which is expected to hold in jammed solids studied here (note that in unjammed states or at low pressure the EMT may not quantitatively apply). As shown in the case of isotropic compression (Eqs. 1–2), the sound speed $V$ can be related to the coordination number $Z$ (Fig. 9), the packing density $\phi$ and the confining pressure $P$.
在本研究中,我们利用线性和非线性相干声传播研究了颗粒形状对颗粒材料力学特性的影响。我们试图在有效介质理论的框架内解释这些观察结果,预计有效介质理论在本文研究的堵塞固体中成立(请注意,在未堵塞状态或低压下,有效介质理论可能无法定量应用)。如各向同性压缩情况所示(式 1-2),声速 $V$ 与配位数 $Z$(图 9)、堆积密度 $\phi$ 和约束压力 $P$ 有关。
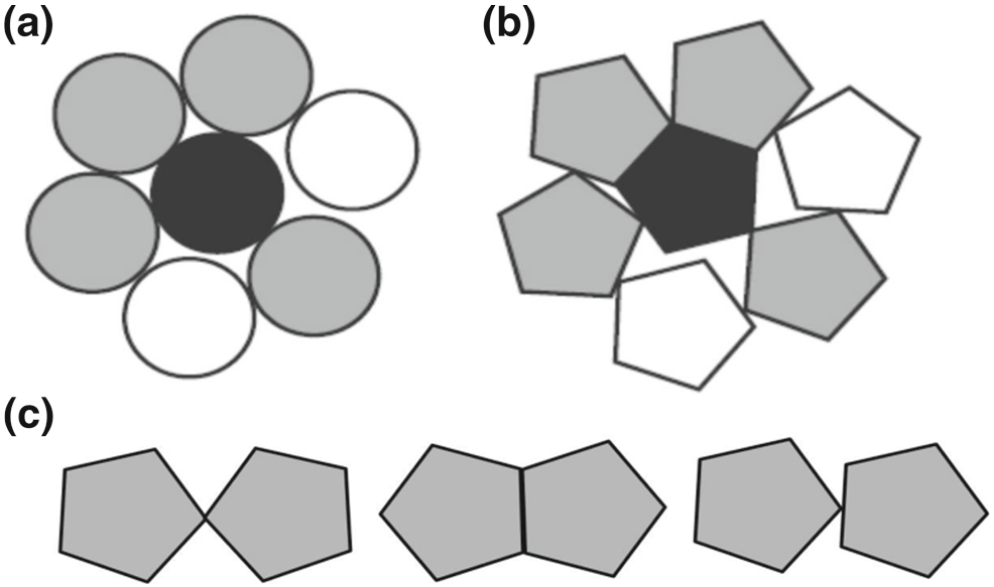
Cartoon of the Coordination number $Z$, the number of contacts with non-zero force, a for glass and b for irregular sand particles. In both cases we draw $Z = 4$. c Schematic of the different possible contacts for irregular particles
a 玻璃和 b 不规则沙粒的配位数(即非零力接触的数量)示意图。在这两种情况下,我们都画出了 $Z = 4$。 c 不规则颗粒的不同可能接触示意图
We have accurately measured the sound speeds in jammed granular solids as a function of the applied uniaxial stress (Fig. 4). We find that our results agree well with scaling law predicted by the EMT, $V\propto P^{1/6}$ (strictly speaking, we should compare our data with an EMT model accounting for the anisotropic stress field; a previous study showed however that the compression sound speed $V$ measured in the direction of the applied uniaxial stress $P$ keeps a scaling behavior very similar to the case of isotropic confining). The solid lines in Fig. 4 represent fits of the EMT (Eqs. 1–2) with a particle shear modulus $G = 29\text{ GPa}$ and Poisson ratio $\nu = 0.2$, typical values for glass materials (see discussion in Sect. 2.1).
我们精确测量了堵塞颗粒固体中的声速与外加单轴应力的函数关系(图 4)。我们发现,我们的结果与 EMT 预测的缩放定律 $V\propto P^{1/6}$ 非常吻合(严格来说,我们应该将我们的数据与考虑了各向异性应力场的 EMT 模型进行比较;但之前的一项研究表明,在施加单轴应力 $P$ 的方向上测量的压缩声速 $V$ 与各向同性约束情况下的缩放行为非常相似)。图 4 中的实线表示 EMT(公式 1-2)与颗粒剪切模量 $G = 29\text{ GPa}$ 和泊松比 $\nu = 0.2$(玻璃材料的典型值)的拟合(见第 2.1 节的讨论)。
In this effective medium model, $Z$ is the only free parameter. By fitting, we find $Z = 6.3$ for glass bead packings, which is a very reasonable value for consolidated granular samples. On the contrary, the data for sand particles suggests a much lower value of $Z = 3.9$. Although such a value for $Z$ appears too low for 3D random close packings of spherical particles, it may be conceivable for sand particle packings. Indeed, the irregular particle shape may lead to interlocking effects that allow for stable granular configurations even for small $Z$.
在这个有效介质模型中,$Z$ 是唯一的自由参数。通过拟合,我们发现玻璃珠堆积的 $Z = 6.3$,这对于固结颗粒样本来说是一个非常合理的值。相反,沙粒的数据表明,$Z$ 值要低得多,为 $Z = 3.9$。虽然对于球形颗粒的三维随机紧密堆积来说,这样的 $Z$ 值似乎过低,但对于沙粒堆积来说,这个值是可以想象的。事实上,不规则的颗粒形状可能会导致连锁效应,即使在 $Z$ 值较小的情况下也能形成稳定的颗粒构型。
Under cyclic loading, the role of the particle shape was also investigated on the mechanical stability of a granular packing. The repetitively applied stress leads to particle motion resulting in a compaction of the granular sample. The EMT predicts that compaction will lead to a decrease of the sound speed according to $V\propto \phi^{-1/6}$, if the coordination number $Z$ and the confining pressure $P$ remain constant. Our experiments on dry glass bead packings show that compaction leads to an increase of the sound speed, in opposition to the EMT prediction. This anomaly may be resolved if we take into account the possible change of the coordination number $Z$.
在循环加载条件下,还研究了颗粒形状对颗粒堆积机械稳定性的作用。重复施加的应力会导致颗粒运动,从而造成颗粒样品的压实。根据 EMT 预测,如果配位数 $Z$ 和约束压力 $P$ 保持不变,压实将导致声速根据 $V\propto \phi^{-1/6}$ 下降。我们在干玻璃珠堆积上的实验表明,压实会导致声速增加,这与 EMT 的预测相反。如果我们考虑到配位数 $Z$ 的可能变化,这种反常现象可能会得到解决。
Indeed, the particle rearrangements, due to the repetitive loading, might break existing contacts or create new contacts, hence $Z$ is not constant. Our sound speed measurements reveal that there is a change in $Z$ due to the particle rearrangements induced by the cyclic loading. Comparison of the data on sand particle and glass bead packings shows that the compaction is similar ($1–2 \%$), however, the change in sound speed is larger for glass beads than for sand particles.
事实上,重复加载导致的粒子重排可能会打破现有的接触或产生新的接触,因此 $Z$ 并非恒定不变。我们的声速测量结果表明,循环加载引起的颗粒重新排列会导致 $Z$ 发生变化。对沙粒和玻璃珠堆积的数据进行比较后发现,压实度是相似的($1-2\%$),但是玻璃珠的声速变化比沙粒大。
This indicates that the compaction is a geometric effect and the relationship between the packing density $\phi(Z)$ and the mechanically loaded coordination number $Z$ depends on the particle shape. Furthermore we find that wetting the granular sample changes the evolution of the sound speed during the cyclic loading.
这表明压实是一种几何效应,而堆积密度 $\phi(Z)$ 与机械加载配位数 $Z$ 之间的关系取决于颗粒形状。此外,我们还发现,在循环加载过程中,润湿颗粒样品会改变声速的演变。
Indeed for wet glass bead packings we observe that the sound speed remains almost constant during the cyclic loading. This may be explained as follows: the oil lubricates the particle contacts and reduces the shear resistance or the internal frictional angle of granular packings; thus the first loading cycle(s) would immediately drive the particles into their most stable configuration and further cycles no longer change significantly the contact structure and $Z$. On the contrary, the compaction is a geometric effect and is little changed by adding the lubricant oil.
实际上,对于湿玻璃珠堆积,我们观察到声速在循环加载过程中几乎保持不变。这可以解释如下:润滑油润滑了颗粒接触,降低了颗粒堆积的剪切阻力或内摩擦角;因此,第一个(多个)加载循环会立即促使颗粒进入最稳定的构型,接下来的循环不会再显著改变接触结构和 $Z$ 值。相反,压实是一种几何效应,加入润滑油后变化不大。
Finally, let us examine nonlinear acoustic responses in weakly compressed sand particle packings where the contact networks are modified but without inducing significant particle motion (the packing density is nearly constant). We found that high-amplitude sound pulses may induce fluctuations in its wave velocity $3\%$ (and amplitude), but significantly smaller than $10\%$ reported for glass bead packings.
最后,让我们研究一下弱压缩沙粒堆积的非线性声学响应,在这种情况下,接触网络会发生改变,但不会引起明显的颗粒运动(堆积密度几乎不变)。我们发现,高振幅声脉冲可能会引起其波速 $3\%$(和振幅)的波动,但明显小于所报告的玻璃珠堆积的 $10\%$(和振幅)。
As suggested previously, we believe that the fluctuations were due to the rearrangements of the contact network, which may result in new contacts (via force chain buckling) or the breaking of existing contacts (via particle sliding). This lower fluctuation compared to glass bead packings may be due to the interlocking effect of the non-spherical sand particles which prevents the particle rearrangements. This underlying physics is supported by a new finding in this work, namely an abrupt increase or decrease of both the sound amplitude and speed.
如前所述,我们认为波动是由于接触网络的重新排列造成的,这种重新排列可能导致新的接触(通过力链屈曲)或现有接触的断裂(通过颗粒滑动)。与玻璃珠堆积相比,波动较小的原因可能是非球形沙粒的连锁效应阻止了颗粒的重新排列。这项工作中的一个新发现支持了这一基本物理原理,即声幅和声速的突然增大或减小。
This abrupt change is likely due to the interlocked particles contacts, which may store applied stress until a certain threshold; after which the contact is broken and the particles suddenly rearrange. This phenomenon makes sand packings brittle, a property not found for glass bead packings where the change in the sound speed is always smooth. Using contact dynamics simulations, it was shown that there is a correlation between $Z$ and the angularity of the particles. Furthermore, it was found that the mechanical stability of the simulated packings depends strongly on the angularity of the particles via the side-side contacts and the mobilization of friction forces. Such a model could account for the interlocking effects described in this study.
这种突然的变化很可能是由于颗粒之间的相互接触造成的,这种接触可以将外加应力储存到某个临界点,之后接触会被打破,颗粒会突然重新排列。这种现象使砂粒堆积变脆,而玻璃珠堆积却没有这种特性,因为玻璃珠堆积的声速变化总是平稳的。通过接触动力学模拟,研究表明 $Z$ 与颗粒的角度之间存在相关性。此外,研究还发现,通过侧面接触和摩擦力的调动,模拟堆积的机械稳定性在很大程度上取决于颗粒的角度。这种模型可以解释本研究中描述的连锁效应。
Conclusion
We have shown that the mechanical behavior such as rigidity of a granular solid is for a large part determined by the particle-level properties like shape and friction. Thanks to accurate acoustic speed measurements, we have observed that packings of angular particles such as sands are more stable than packings of glass beads, probably due to interlocking effects between angular particles. Compared to spherical particles, this interlocking effect has three consequences: (i) it allows for stable packings with small coordination number $Z$; (ii) the fluctuations in the contact number $Z$ caused by either mechanical loading or high-amplitude sound transmission are reduced; (iii) packings of angular particles are brittle, resulting in occasional abrupt changes in $Z$.
我们已经证明,颗粒固体的机械行为(如刚性)在很大程度上是由颗粒级特性(如形状和摩擦力)决定的。借助精确的声速测量,我们观察到,与玻璃珠相比,有棱角的颗粒(如沙)的堆积更稳定,这可能是由于有棱角的颗粒之间的连锁效应。与球形颗粒相比,这种互锁效应有三种结果:(i)它使配位数 $Z$ 较小的稳定堆积成为可能;(ii)减少了由机械负荷或高振幅声音传播引起的接触数 $Z$ 的波动;(iii)含棱角颗粒堆积较脆,导致 $Z$ 偶尔发生突然变化。
We believe that our acoustic method could be useful for characterising the structure and the dynamic response of jammed aggregate states, which are controlled by the particle-level properties and packing arrangement.
我们相信,我们的声学方法可用于描述受颗粒级特性和堆积排列控制的堵塞集料状态的结构和动态响应。

