Abstract
The dissipation of an elastic wave in dry and wet glass bead packings is measured using multiple sound scattering. The interplay of a linear viscoelastic loss and a nonlinear frictional one is observed in dry media. The Mindlin model provides a qualitative description of the experiment, but fails to quantitatively account for the data due to grain roughness. In weakly wet media, we find that the dissipation is dominated by a linear viscous loss due to the liquid films trapped at the grain surface asperities. Adding more liquid enables us to form the capillary menisci but does not increase the energy loss.
利用多重声散射测量了弹性波在干燥和潮湿玻璃珠堆积中的耗散。在干燥介质中观察到线性粘弹性损耗和非线性摩擦损耗的相互作用。Mindlin 模型对实验进行了定性描述,但无法定量解释颗粒粗糙度影响的数据。在微湿介质中,我们发现耗散主要是由滞留在颗粒表面粗糙处的液体薄膜造成的线性粘性损耗。添加更多的液体能让我们形成毛细半月板,但并不会增加能量损失。
Introduction
The attenuation of elastic wave in earth materials has been the subject of extensive investigations for many years in the fields of both seismology and rock physics. The acoustic properties of porous granular materials such as sedimentary rocks, ocean sediments, and sintered bead packs are in general characterized by the properties of solid frame, the pore fluid if any, and frame-fluid interactions.
Several mechanisms of intrinsic attenuation have been proposed, including the Coulomb frictional sliding between cracks and grain boundary contacts and the linear mechanism dominated by viscous dissipation of bulk fluid flow in partially or fully saturated rocks. In room-dry rocks containing small amount of volatiles, it is found that the attenuation is caused by another linear mechanism, due to a stress-induced diffusion of adsorbed monolayers of volatiles.
多年来,地震学和岩石物理学领域一直在广泛研究弹性波在地质材料中的衰减问题。多孔颗粒材料(如沉积岩、海洋沉积物和烧结珠块)的声学特性一般由固体框架、孔隙流体(如有)以及框架与流体之间的相互作用所决定。
已经提出了几种内在衰减机制,包括裂缝和晶界接触之间的库仑摩擦滑动,以及部分或完全饱和岩石中散装流体粘性耗散主导的线性机制。在含有少量挥发物的常干性岩石中,研究发现衰减是由另一种线性机制引起的,这是由于吸附单层挥发物的应力诱导扩散所致。
Noncohesive granular materials are composed of a dense random packing of macroscopic particles. Unlike consolidated porous materials, granular materials acquire basically its elasticity as a result of the applied stresses, forming the very inhomogeneous force network—a solid frame. In the long-wavelength limit, the elastic wave propagation can be described by the effective medium approach based on the Hertz-Mindlin theory of contact at the grain level. Similar to porous rocks, a small amount of liquid has a drastic effect on the mechanical properties of granular materials, such as the angle of avalanche and sound propagation.
非粘性颗粒材料由宏观颗粒的密集随机堆积组成。与固结的多孔材料不同,颗粒材料在外加应力的作用下基本上获得了弹性,形成了非常不均匀的力网络–固体框架。在长波极限下,弹性波的传播可以用有效介质方法来描述,该方法基于颗粒级接触的 Hertz-Mindlin 理论。与多孔岩石类似,少量液体也会对颗粒材料的机械特性产生剧烈影响,如雪崩角和声音传播。
Pilbeam and Vaisnys have measured acoustic velocity and attenuation in dry and lubricated granular materials. They found that measured velocities in all the samples could be understood on the basis of the Hertz-Mindlin contact theory.
However, such nonlinear friction theory does not adequately account for the behavior of energy dissipation observed in their experiments essentially independent of wave (strain) amplitude, a feature suggesting a linear mechanism for attenuation. This experimental observation raises an important question: Is it possible to reconcile a nonlinear frictional dynamics and a linear mechanism of dissipation at the grain contact level, particularly in the presence of adsorbed films?
Pilbeam 和 Vaisnys 测量了干燥和润滑颗粒材料中的声速和衰减。他们发现,根据 Hertz-Mindlin 接触理论,可以理解所有样品中测得的速度。
然而,这种非线性摩擦理论并不能充分解释他们在实验中观察到的能量耗散行为,这种行为基本上与波振幅(应变)无关,这一特征表明衰减是一种线性机制。这一实验观察结果提出了一个重要问题:在晶粒接触层面,特别是在存在吸附膜的情况下,是否有可能在非线性摩擦动力学和线性耗散机制两者之间做出协调?
In this Letter, we address this question by presenting new experimental results of elastic wave dissipation $Q^{-1}$ obtained in dry and weakly wet granular materials by using codalike multiply scattered elastic waves. Particular attention will be focused on the influence of surface properties of grains by adding a small amount of liquid or with adsorbed films. Compared to low-frequency waves, the high-frequency scattered waves have the advantage of separating the intrinsic attenuation from the scattering attenuation and infer the material properties on smaller length scales of the order of wavelength.
在这封快讯中,我们针对这一问题,介绍了在干燥和弱湿颗粒材料中使用同源多散射弹性波获得的弹性波耗散 $Q^{-1}$ 的新实验结果。我们将特别关注通过添加少量液体或吸附层对颗粒表面特性的影响。与低频波相比,高频散射波具有将本征衰减与散射衰减分开的优势,可以推断出波长数量级的较小长度尺度上的材料特性。
Experiments
Our granular media are composed of slightly polydisperse glass beads of diameter $2R = 0.6–0.8\text{ mm}$ manufactured for use as an abrasive (from Centraver). Clean granular samples are achieved by successively rinsing glass beads with acetone, ethanol, sulfochromic acid, and distilled water; the beads are then dried in a furnace. To study the effects of surface properties, small amounts of wetting liquid (volume fraction $\varphi_{\text{liq}} = 0.05$%) are added to glass beads. Here we used different silicon oils as wetting liquids to minimize the effects of evaporation. The kinematic viscosities of silicon oils (Rhodorsil 47V) $\nu_{\text{liq}}$ vary from 5 to 100 centistokes (cSt) due to their composition, possessing nevertheless the same density $\rho_{\text{liq}}$ and tension surface $\gamma_{\text{liq}}$.
我们的颗粒介质由直径为 $2R = 0.6-0.8\text{ mm}$ 的轻微多分散玻璃珠组成,这些玻璃珠是为用作研磨物而制造的(来自 Centraver)。通过用丙酮、乙醇、磺酸和蒸馏水连续冲洗玻璃珠,可获得 清洁 的颗粒状样品;然后将玻璃珠放入熔炉中烘干。为了研究表面特性的影响,我们在玻璃珠中加入了少量润湿液(体积分数 $\varphi_{\text{liq}} = 0.05$%)。在这里,我们使用不同的硅油作为润湿液,以尽量减少蒸发的影响。硅油(Rhodorsil 47V)的流动粘度 $\nu_{\text{liq}}$ 因其成分而异,从 5 厘沲(cSt)到 100 厘沲(cSt)不等,但具有相同的密度 $\rho_{\text{liq}}$ 和表面张力 $\gamma_{\text{liq}}$。
The glass beads are mixed vigorously during tens of minutes to evenly distribute the liquid among the grains. Our glass beads are poured into a duralumin cylinder of diameter 30 mm and height 11 mm, layer by layer followed by successive compactions. A normal stress $P_{0}$ ranging from 0.1 to 1 MPa is then applied to the granular sample. Before each measurement, one cycle of loading and unloading is performed to the granular packing in order to consolidate the sample and minimize its hysteretic behavior. The solid volume fraction is about $\varphi_{\text{sol}}\approx 63$ % and 61% for dry and wet granular packings, respectively.
玻璃珠经过数十分钟的剧烈搅拌,使液体均匀分布在微粒之间。将玻璃珠逐层倒入直径为 $30$ 毫米、高为 $11$ 毫米的硬铝圆筒中,然后进行连续压实。然后在颗粒样品上施加 $0.1$ 至 $1$ 兆帕的法向应力 $P_{0}$。每次测量前,都要对颗粒堆积进行一次加载和卸载循环,以固化样品并尽量减少其滞后行为。干颗粒堆积和湿颗粒堆积的固体体积分数分别约为 $\varphi_{\text{sol}}\approx 63$% 与 $61$%。
A longitudinal source transducer of diameter 30 mm and a small detecting transducer of diameter 2 mm are then placed on the axis of the cylindrical cell of diameter 30 mm in contact with glass beads. Fifteen-cycle tone burst excitations centered at $f(=\omega/2\pi)= 500\text{ kHz}$ are applied to the calibrated source transducer and the granular sample is subjected to 1 min of sound vibration before each acoustic measurement to ensure a better reversibility.
然后将一个直径为 $30$ 毫米的纵向声源换能器和一个直径为 $2$ 毫米的小型检测换能器放置在直径为 $30$ 毫米的圆柱形样品池的轴线上,并与玻璃珠接触。以 $f(=\omega/2\pi)= 500\text{ kHz}$ 为中心的 $15$ 个周期的音爆激励被施加到校准过的声源换能器上,每次声学测量前,颗粒样品都要经过 $1$ 分钟的声振,以确保更好的可逆性。
Figure 1 illustrates a typical ultrasound transmission $s(t)$ through a dry glass bead packing under $P_{0} = 0.62\text{ MPa}$ and excited by the source displacement $u\approx 15\text{ nm}$, corresponding to an acoustic strain $\epsilon(=\omega u/c_{0})\approx 4.5\times 10^{5}$ with the compressional wave velocity $c_{0}\approx 980\text{m /s}$ in the granular medium. The transmitted intensity of multiply scattered ultrasounds dominated by shear waves due to mode conversion, $I(t)$(~$\langle s(t)^{2}\rangle$), is obtained by ensemble averaging over 50 independent configurations. By fitting the intensity profile with a diffusion model, we extract the internal dissipation $Q^{-1}$ (the ratio of energy loss per cycle to peak energy stored) via the quality factor $Q(\approx 295\pm 5)$, and the diffusion constant $D(\approx 0.095\pm 0.005\text{ m}^{2}\text{/s})$.
图 1 展示了在 $P_{0} = 0.62\text{ MPa}$,并由源位移 $u\approx 15\text{ nm}$ 激发,对应于颗粒介质中的声学应变 $\epsilon(=\omega u/c_{0})\approx 4.5\times 10^{5}$,压缩波速度 $c_{0}\approx 980\text{m /s}$。通过对 $50$ 个独立进行系综平均,可以得到由模式转换引起的剪切波主导的多重散射超声波的透射强度 $I(t)$(~$\langle s(t)^{2}\rangle$)。通过用扩散模型拟合强度曲线,我们通过品质因数 $Q(\approx 295\pm 5)$ 和扩散常数 $D(\approx 0.095\pm 0.005\text{ m}^{2}\text{/s})$ 提取出内部耗散 $Q^{-1}$(每个周期的能量损失与存储峰值能量之比)。
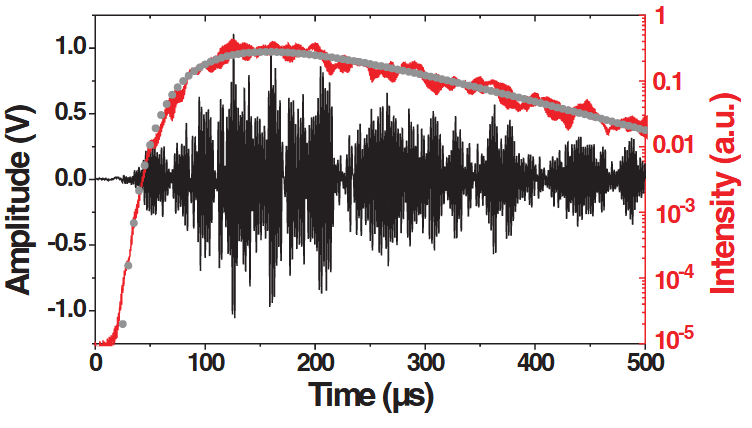
Specklelike scattered ultrasound through a dry granular packing (black curve) and the transmitted intensity $I$ averaged over $50$ configurations [red (gray) curve]. Gray circles refer to the fit.
通过干燥颗粒状堆积的斑点状散射超声波(黑色曲线)和 $50$ 种配置的平均透射强度 $I$ [红色(灰色)曲线]。灰⚪指的是拟合。
We first investigate the effect of strain amplitude on the internal dissipation. Figure 2 represents $Q^{-1}$ measured as a function of the source amplitude in dry and wet glass bead packings, respectively. In dry granular samples, cleaned or not, $Q^{-1}$ increases linearly with strain indicating a non- linear regime of dissipation, and tends to a finite constant at small strain. Moreover, it is found that cleaning the glass beads permits one to reduce the dissipation, presumably due to the removal of dust layers from the grain surfaces.
我们首先研究应变振幅对内部耗散的影响。图 2 分别表示在干玻璃珠和湿玻璃珠堆积中测量到的 $Q^{-1}$ 与源振幅的函数关系。在干颗粒样品中,无论是否清洁,$Q^{-1}$ 都随应变线性增加,表明耗散为非线性状态,在小应变时趋于有限常数。此外,研究还发现,清洁玻璃珠可以降低耗散,这可能是由于清除了晶粒表面的灰尘层。
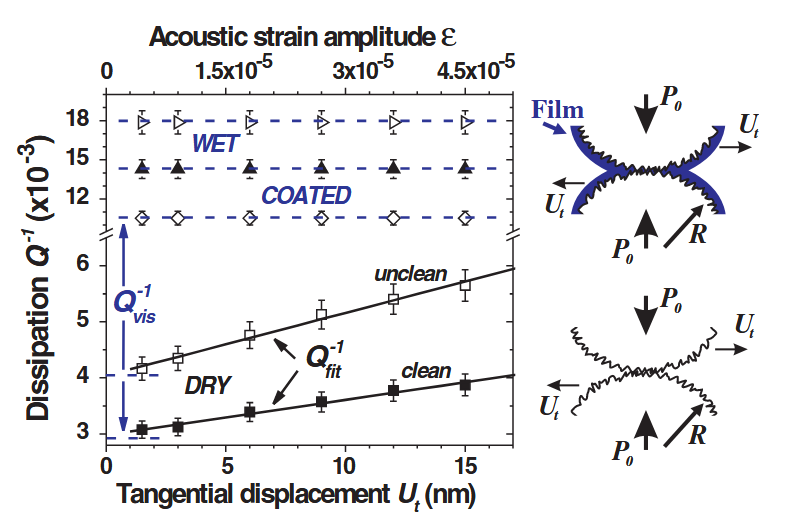
$Q^{-1}$ versus strain amplitude $\epsilon$ for different granular packings under $P_{0} = 0:62\text{ MPa}$: clean (黑方块), unclean (白方块), silanized (菱形), and wet glass beads by silicon oil 47V10 (黑三角) and 47V100 (白三角). Dashed lines refer to viscous behaviors $Q_{\text{vis}}^{-1}$ (see the text), and solid lilnes to the fits Insets: Schemata of grain contacts between dry and coated beads by solid or liquid film.
在 $P_{0} = 0:62\text{ MPa}$ 条件下,不同颗粒堆积的 $Q^{-1}$ 与应变幅度 $\epsilon$ 的关系:在硅油 47V10 (黑三角) 和 47V100 (白三角) 的作用下,清洁 (黑方块)、不清洁 (白方块)、硅烷化 (菱形) 和湿玻璃珠。虚线指的是粘性行为 $Q_{\text{vis}}^{-1}$(见正文),实线指的是拟合. 插图:干珠与固膜或液膜包覆珠之间的颗粒接触示意图。
In order to explore the effects of adsorbed film on grain surface, we conduct measurements of the $Q^{-1}$ in a packing of glass beads coated by a hydrophobic film (silanized layer) of about 100 nm in thickness. The presence of the adsorbed solid film significantly increases the dissipation by a factor of about 3 as shown in Fig. 2, and results in a $Q^{-1}$ nearly independent of strain amplitude over our experimental range. Similar behavior of dissipation is also found in the wet bead packing by silicon oils (Fig. 2).
为了探索吸附膜对颗粒表面的影响,我们测量了玻璃珠堆积中厚度约为 $100\text{ nm}$ 的疏水膜(硅烷化层)的 $Q^{-1}$。如图 2 所示,吸附固体薄膜的存在使耗散显著增加了约 $3$ 倍,并导致在我们的实验范围内,$Q^{-1}$ 与应变振幅几乎无关。在硅油湿珠堆积中也发现了类似的耗散现象(图 2)。
The wetting liquids form an adsorbed film of the order of the asperities (~100 nm). Measured $Q^{-1}$ increases by a factor of 5–10, and the higher the liquid viscosity, the larger the dissipation $Q^{-1}$. In addition, $Q^{-1}$ measured is again found to be independent of the strain amplitude, pointing to a dominant linear mechanism of dissipation. These results are different from those observed in dry media.
润湿液体形成的吸附膜的(厚度)数量级为表面凸起峰(高度)(~100 nm)。测得的 $Q^{-1}$ 增加了 $5-10$ 倍,并且液体粘度越高,耗散 $Q^{-1}$ 越大。此外,测量到的 $Q^{-1}$ 也与应变振幅无关,这表明线性耗散机制占主导地位。这些结果与在干燥介质中观察到的结果不同。
Analysis and discussion
To account for the experimental observation of elastic wave dissipation, we com- pare the measured $Q^{-1}$ with some of the predictions by the contact theory. As a first approach to the problem, the model for the glass bead packing may be taken as a homogeneous random contact network of uniform spheres $2R$. The bulk elastic and dissipative responses of the granular system are thus directly related to the dynamic properties of the individual contact (cf. insets of Fig. 2).
为了解释实验观察到的弹性波耗散,我们将测量到的 $Q^{-1}$ 与接触理论的一些预测进行了比较。作为解决问题的第一种方法,玻璃珠堆积模型可视为均匀球体 $2R$ 的均质随机接触网络。因此,颗粒系统的体弹性和耗散响应与单个接触的动态特性直接相关(参见图 2 的插图)。
When such a contact is submitted to a shear force $F_{t}\leq \mu F_{n}$ with $F_{n}$ the normal load and $\mu$ the friction coefficient, Mindlin has shown that the interfacial normal and shear stiffness, $k_{n}$ and $k_{t}$, are comparable. For the oscillating amplitudes of normal and shear displacement at the contact surfaces, $U_{n}$ and $U_{t}$, the peak strain energy stored is $W = \frac{1}{2}k_{n}U_{n}^{2} + \frac{1}{2}k_{t}U_{t}^{2}$. The energy dissipation per cycle $\Delta W$ at each contact should then be evaluated in order to determine $Q^{-1} = \Delta W /(2\pi W)$.
当这种接触受到剪切力 $F_{t}\leq \mu F_{n}$ (其中 $F_{n}$ 是法向应力,$\mu$ 是摩擦系数)作用时,Mindlin 证明界面法向刚度和剪切刚度 $k_{n}$ 和 $k_{t}$ 是相当的。对于接触面的法向位移和剪切位移的振荡振幅 $U_{n}$ 和 $U_{t}$,存储的峰值应变能为 $W = \frac{1}{2}k_{n}U_{n}^{2}+ \frac{1}{2}k_{t}U_{t}^{2}$。然后,应评估每个接触点每个周期的能量耗散 $\Delta W$,以确定 $Q^{-1} = \Delta W /(2\pi W)$。
In the dry bead packing, we examine the prediction by the Mindlin theory, the most widely used model describing the friction between two smooth spheres. At low oscillating amplitude $\delta W_{\text{fric}}$ is proportional to $F_{t}^{3}$ or $U_{t}^{3}$ and $Q_{\text{fric}}^{-1}$ is written as
$$ Q_{\text{fric}}^{-1} = \left[\frac{4G}{9\pi^{2}(2-\nu)R}\left(\frac{3\pi}{4E^{*}}\right)^{\frac{1}{3}}\right]\mu^{-1} P_{0}^{-\frac{2}{3}}U_{t}, $$
where $\nu$, $E^{*}$, and $G$ are the Poisson ratio, bulk, and shear modulus of the glass material, respectively, and $P_{0} = F_{0}/(\pi R^{2})$. The most prominent feature of Eq. (1) is the amplitude dependence of $Q^{-1}_{\text{fric}}$, characteristic of a nonlinear frictional attenuation.
在干珠堆积中,我们研究了 Mindlin 理论的预测结果,该理论是描述两个平滑球体之间摩擦力的最广泛使用的模型。在低振荡幅度下,$W_{\text{fric}}$ 与 $F_{t}^{3}$ 或 $U_{t}^{3}$ 成正比,$Q_{\text{fric}}^{-1}$ 可以写为
$$ Q_{\text{fric}}^{-1} = \left[\frac{4G}{9\pi^{2}(2-\nu)R}\left(\frac{3\pi}{4E^{*}}\right)^{\frac{1}{3}}\right]\mu^{-1} P_{0}^{-\frac{2}{3}}\color{red}{U_{t}} $$
其中,$\nu$、$E^{*}$ 和 $G$ 分别是玻璃材料的泊松比、体积和剪切模量,$P_{0} = F_{0}/(\pi R^{2})$ 。公式 (1) 的最显著特点是 $Q^{-1}_{\text{fric}}$ 的 $\color{red}{\text{振幅}}$ 依赖性,这是非线性摩擦衰减的特征。
This theory provides a simple inter- pretation of the increasing of $Q^{-1}$ with the strain amplitude. Note that such nonlinear hysteretic attenuation is also found in a large class of earth materials. However, the frictional dissipation at small strains either disappears or becomes masked by amplitude-independent (linear) dissipation mechanism as observed in Fig. 2. Similarly, a linear dissipation regime was evidenced for small-strain oscillation of a steel sphere in contact with a flat glass surface by Johnson, and between two identical rough solids by Bureau et al.. The loss mechanism is ascribed to the linear viscoelastic dissipation within the bodies of contacting asperities.
这一理论为 $Q^{-1}$ 随应变振幅的增加提供了一个简单的相互印证。需要注意的是,这种非线性滞后衰减也存在于一大类土材料中。然而,如图 2 所示,小应变时的摩擦耗散要么消失,要么被与振幅无关的(线性)耗散机制所掩盖。同样,Johnson 的研究和 Bureau 等人的研究也证明了钢球与玻璃表面接触时的小应变振荡和两个相同粗糙固体之间的线性耗散机制。这种损耗机制归因于接触表面体内部的线性粘弹性耗散。
As a result, the interfacial dissipation is described by the interplay of two mechanisms:
$$ Q^{-1} = Q_{\text{fric}}^{-1} + Q_{\text{vis}}^{-1}. $$
Using the material constants of glass, $G = 28\text{ GPa}$, $E^{*} = 37\text{ GPa}$, $\nu = 0.25$, one can extract by fitting Eq. (2) both the $Q_{\text{vis}}^{-1}$ and the friction coefficient $\mu$. For $P_{0} = 0.62\text{ MPa}$, one obtains by fit $Q_{\text{vis}}^{-1}\approx 4\times 10^{-3}$ and $\mu\approx 0.98$ for unclean bead packing, and $Q_{\text{vis}}^{-1}\approx 3\times 10^{-3}$ and $\mu\approx 1.75$ for clean bead packing, respectively.
因此,界面耗散是通过两种机制的相互作用来描述的:
$$ Q^{-1} = Q_{\text{fric}}^{-1} + Q_{\text{vis}}^{-1}. $$
Note that the deduced $Q_{\text{vis}}^{-1}$ is much larger than that of the bulk glass $Q_{\text{glass}}^{-1}$(~$10^{-6}$), pointing thus to the interfacial dissipation which we speculate is due to the viscoelastic loss within a contacting layer different from the bulk of the glass bead. Moreover, as expected, the friction coefficient of unclean beads is smaller than that of clean beads, probably due to the presence of the dust film on glass bead surfaces which form effective lubricants and enhance sliding dissipation. However, the absolute values of the friction coefficient deduced are unusually high ($\mu_{\text{glass}}\approx 0.3$).
请注意,推导出的 $Q_{\text{vis}}^{-1}$ 远大于块状玻璃的 $Q_{\text{glass}}^{-1}$(~$10^{-6}$),这说明存在界面耗散,我们推测这是由于不同于玻璃珠块体的接触层内的粘弹性损失造成的。此外,正如预期的那样,未清洁珠子的摩擦系数小于清洁珠子的摩擦系数,这可能是由于玻璃珠表面存在灰尘膜,形成了有效的润滑剂,增强了滑动耗散。然而,推导出的摩擦系数绝对值却异常之高($\mu_{\text{glass}}\approx 0.3$)。
As revealed in a recent work, the Mindlin model fails to describe quantitatively the dissipative response on rough interfaces, because the use of local friction coefficient is legitimate only when the width L of the microslip zone is much larger than hundreds of nm. However, this condition is not satisfied by the small-amplitude shear oscillating, e.g., $\varepsilon\approx 10^{-5}$, which produce merely a $L$ of about $300\text{ nm}$.
最近的一项研究表明,Mindlin 模型无法定量描述粗糙界面上的耗散响应,因为只有当微滑区的宽度 $L$ 远大于数百 $\text{nm}$ 时,使用局部摩擦系数才是合理的。然而,小振幅剪切振荡(例如:$\varepsilon\approx 10^{-5}$)并不满足这一条件,它仅仅产生约 $300\text{ nm}$ 的 $L$。

