贾小平
Abstract
We study the multiple scattering of short-wavelength ultrasound through the force networks in dry and wet glass bead packings under stress. Over long distance scales, the diffusion approximation is shown to describe adequately the transport of elastic waves dominated by shear waves.
The recovered transport mean path reveals a short-range correlation of the force chains. Also we observe the drastic effect of wetting liquids on the energy dissipation in the granular medium. The relevance of these experimental findings for the seismological applications is discussed.
我们研究了在应力作用下, 短波长超声波通过干/湿玻璃珠堆积中的力网络产生的多重散射. 结果表明, 在长距离尺度上, 扩散近似 能充分描述以剪切波为主的弹性波的传输.
恢复的传输平均程显示了力链的短程相关性. 此外, 我们还观察到湿润液体对颗粒介质中能量耗散的剧烈影响. 我们讨论了这些实验发现与地震学应用的相关性.
The physics uncovered in granular materials has clear relevance to a wide variety of dissipative, nonequilibrium systems, including glasses and dense colloidal suspensions, and also on a much larger scale to nonlinear phenomena such as avalanche and earthquake dynamics.
In noncohesive granular materials, photoelastic visualization experiments and simulations show that the contact forces arising as a result of the external load are distributed in a very inhomogeneous fashion, forming a network of percolating force chains.
It is this network of contacts that determines most salient mechanical properties of a dense granular medium such as its ability to bear a load, nonlinear elastic response, and flow behavior.
在颗粒材料中发现的物理学原理显然与玻璃和致密胶体悬浮液等各种耗散非平衡系统有关, 而且与雪崩和地震动力学等更大规模的非线性现象有关.
在非粘性颗粒材料中, 光弹性可视化实验和模拟显示, 由于外部载荷而产生的接触力分布非常不均匀, 形成了一个由渗流力链组成的网络.
正是这种接触网络决定了致密颗粒介质(DGM, Dense Granular Media)最显著的机械特性, 如承受载荷的能力、非线性弹性响应和流动行为.
Introduction
Small amplitude compressional and shear acoustic waves provide a unique noninvasive probe of both the structure and the nonlinear elastic properties of the force network within real $3$D granular media.
At low frequencies such that the wavelengths are very long compared to the correlation length of force chains, the granular medium is effectively a homogeneous continuum to the propagating wave.
At high frequencies when the wavelength decreases down to the order of the grain size, scattering effects caused by the spatial fluctuations of force chains become very significant and the effective contact medium is no longer a valid description.
In this regime, scattered sound waves are configuration specific determined by the exact structure of the force chains, which provide a sensitive tool for studying configurational variations of the contact network.
小振幅压缩声波和剪切声波提供了一种独特的非侵入式探针, 可探测实际 $3$D 颗粒介质中力网络的结构和非线性弹性的特性.
在低频情况下, 与力链的相关长度对比, 颗粒介质的波长非常长, 因此对于传播的波来说, 颗粒介质实际上是一个均匀的连续体.
在高频率下, 当波长减小到晶粒大小的数量级时, 力链的空间波动引起的散射效应变得非常显著, 有效接触介质不再是有效的描述.
在这种情况下, 散射声波是由力链的精确结构决定的特定构型, 这为研究接触网络的构型变化提供了一个灵敏的工具.
However, up to now, it remains unclear whether the multiple scattering of elastic waves in a granular medium can be described in the framework of classical diffusive propagation such as light and sound in a strongly scattering random medium, or whether it is fundamentally different than in other random media, as suggested by Liu and Nagel, due to the presence of a few dominating paths created by the force chains along which sound waves at all frequencies must pass through.
Addressing this question is also of considerable interest for seismological applications, which enable one to gain insight into the role of short-wavelength acoustic emission in the fault dynamics. In this Letter, we test the application of the diffusion approximation to the propagation of high-frequency ultrasounds in glass bead packings under stress.
We show that the multiple scattering of elastic waves allow inferring the material properties such as the correlation length of the force chain structure and the internal dissipation, on small length scales not accessible by long-wavelength coherent waves.
然而, 迄今为止, 人们仍不清楚弹性波在颗粒介质中的多重散射是否可以在经典扩散传播的框架内进行描述, 例如光和声在强散射随机介质中的传播, 或者是否如 Liu 和 Nagel 所言, 由于存在由力链创建的少数主导路径, 所有频率的声波都必须沿着这些路径通过, 因此弹性波在颗粒介质中的多重散射与在其他随机介质中的多重散射有着本质区别.
解决这个问题对地震学应用也有相当大的意义, 它能让我们深入了解短波声发射在断层动力学中的作用. 在这封信中, 我们测试了扩散近似在应力作用下高频超声波在玻璃珠堆积中传播的应用.
我们发现, 通过弹性波的多重散射, 可以在小长度尺度上(通常长波长相干波无法到达)推断出材料特性, 如力链结构的相关长度和内部耗散.
Experiment
The glass beads used in our experiments are of diameter $d = 0.6-0.8$ mmm, randomly deposited by pouring and stirring in a duralumin cylinder of diameter $W = 30$ mm and varying height from $7$ to $15$ mm. The container is closed with two fitting pistons and a normal load is applied to the granular sample across the top piston. Before the ultrasonic measurements, one cycle of loading and unloading is performed in the granular packing in order to consolidate the sample and minimize its hysteretic behavior.
实验中使用的玻璃珠直径为 $0.6-0.8\text{mm}$, 通过浇注和搅拌随机沉积在直径为 $30\text{mm}$ 、高度为 $7-15\text{mm}$ 的硬铝圆筒中. 容器由两个配合活塞封闭, 并在顶部活塞上对颗粒样品施加法向载荷. 在进行超声波测量之前, 先在颗粒堆积中进行一个加载和卸载循环, 以加固样品并尽量减少其滞后行为.
Statistically independent ensembles of the packing configuration are realized by stirring vigorously glass beads after each measurement and repeating carefully the same loading protocol. The volume fraction of glass beads thus obtained is found to be $0.63\pm 0.01$.
A plane-wave generating transducer of diameter $30$ mm(top piston) and a small detecting transducer of diameter $2$ mm are placed on the axis at the top and the bottom of the cylindrical container in direct contact with glass beads (Fig. 1).
通过在每次测量后剧烈搅拌玻璃珠并仔细重复相同的加载协议, 可实现统计独立的堆积构型系综. 由此得到的玻璃珠体积分数为 $0.63\pm 0.01$. 一个直径为 $30\text{mm}$ 的平面波传感器(顶部活塞)和一个直径为 $2\text{mm}$ 的小型检测传感器分别放置在圆柱形容器顶部和底部的轴线上, 与玻璃珠直接接触(图 1).
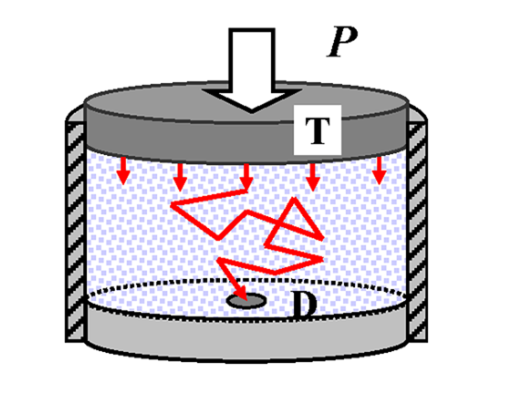
Multiple scattering of elastic waves in a confined granular packing under stress $P$. “T” and “D” denote the large source transducer and the small detector, respectively.
在应力 $P$ 的作用下, 弹性波在密闭颗粒堆积中的多次散射. “T” 和 “D” 分别表示大源传感器和小探测器.
Unlike the previous experiment using a broadband short pulse, ten-cycle tone burst excitations of $20\mu$s duration centered at a frequency of $500\text{kHz}$ are applied to the longitudinal source transducer.
This narrow band excitation corresponds to the product of granular skeleton acoustic wave number and bead diameter, $kd = \omega d/v \approx 2.9$, with $v= 750\text{m/s}$ being a typical sound speed in the solid frame. At such a high frequency, one expects to deal with a strongly scattering medium.
与之前使用宽带短脉冲的实验不同, 本次实验往纵向源传感器施加了持续时间为 $20\mu$s 的十周期音爆激励, 中心频率为 $500\text{kHz}$.
这种窄带宽激励相当于粒状骨架声波的波数与珠子直径的乘积, $kd = \omega d/v \approx 2.9$, 其中 $v= 750\text{m/s}$ 是固体框架中的典型声速. 在如此高的频率下, 我们希望处理的是强散射介质.
In Fig. 2(a), we show the ultrasound propagating through a glass bead packing of thickness $L = 11.4\text{mm}$ under axial stress of $P = 750\text{kPa}$, a typical pressure at depths of tens of meters in soils due to the weight of the overburden.
As previously, the transmitted temporal signal consists basically of a primary coherent component and a strongly fluctuating incoherent component.
The low-frequency coherent pulse $E_{p}$(
$70\text{kHz}$) at the leading edge of the transmitted signal corresponds to a selfaveraging effective wave propagating ballistically at compressional wave velocity $v_{p}\approx 1000\text{m/s}$, while the high-frequency incoherent signal $S$($500\text{kHz}$) arriving mostly at later times is devoted to specklelike scattered waves by the inhomogeneous distribution of force chains.
在图 2(a)中, 我们展示了超声波在厚度为 $L = 11.4\text{mm}$ 的玻璃珠堆积中传播的情况, 其轴向应力为 $P = 750\text{kPa}$, 这是由于覆土的重量而在数十米深的土壤中产生的典型压强.
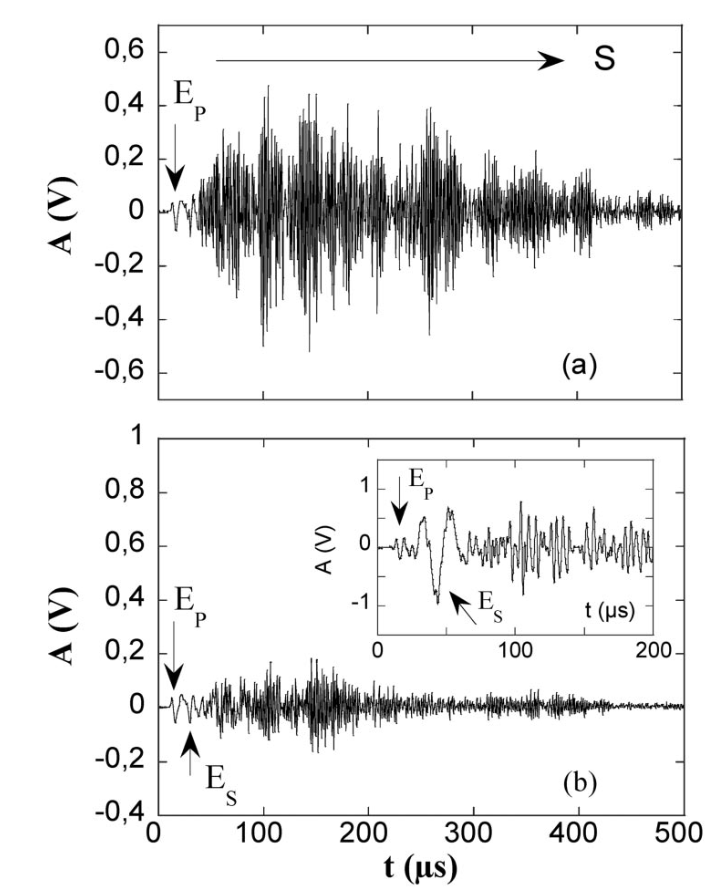
Transmitted ultrasonic signals through a dry glass beads packing (a) at a given configuration, and (b) after ensemble averaging over 15 independent configurations. The inset illustrates the transmitted signal at a given configuration using the shear transducers.
通过干玻璃珠堆积传输的超声波信号 (a) 在给定构型下, 以及 (b) 对 15 个独立配置进行系综平均后. 插图显示了使用剪切传感器在给定构型下的传输信号.
如前所述, 传输的时间信号基本上由一个主要的相干分量和一个强烈波动的非相干分量组成.
传输信号前沿的低频相干脉冲 $E_{p}$($70\text{kHz}$)对应于以压缩波速度 $v_{p}\approx 1000\text{m/s}$ 进行轨道传播的自平均有效波, 而主要在后期到达的高频非相干信号 $S$($500\text{kHz}$)则是由不均匀分布的力链产生的斑点状散射波.
The sensitivity of the coherent and incoherent waves to changes in packing configurations is shown in Fig. 2(b) by ensemble averaging the transmitted ultrasonic signals over $15$ independent granular samples.
Because of the random phases of the scattered signals from independent packing configurations, the scattered waves tend to cancel out each other in averaging, leaving the ballistic coherent pulse $E_{p}$ which is self-averaged and consequently configuration insensitive.
Moreover, another coherent signal noted as $E_{S}$ survives from this averaging procedure, which propagates ballistically at a shear velocity about $v_{S} = 450\text{m/s}$.
As shown in the inset of Fig. 2(b), the use of large transverse transducers can lead to a considerable enhancement of this shear wave.
图 2(b) 显示了相干波和非相干波对堆积结构变化的敏感性, 即对 $15$ 种独立颗粒样本的透射超声波信号进行系综平均.
由于来自独立堆积构型的散射信号的相位是随机的, 因此散射波在平均时往往会相互抵消, 剩下的弹道相干脉冲 $E_{p}$ 是自平均的, 因此对构型不敏感.
什么是"self-averaged"?
我们称一个物理量为自平均, 即意味着它的平均值不依赖于样本的大小或者随机性, 而是由系统的性质决定的.
此外, 在这一平均过程中还存在另一个相干信号 $E_{S}$, 它以大约 $v_{S} = 450\text{m/s}$ 的剪切速度轨道传播. 如图 2(b)的插图所示, 使用大型横向传感器可显著增强这种剪切波.
To investigate the statistical characteristics of scattered waves, we follow the intensity evolution in space and time of the wave train injected into the granular medium.
For each configuration we subtract the low-frequency coherent ballistic pulses $E_{P}$ and $E_{S}$ from the transmitted signal [Fig. 2(a)] by means of a high-pass (HP) filter ($f \geq 300 \text{kHz}$), either analogical or numerical, and determine the intensity of the scattered waves by squaring the envelope of the filtered waveform.
In Fig. 3, we show on a semilogarithmic scale the resulting transmitted intensity of a scattered waves ensemble averaged over 50 independent configurations for three different sample thicknesses. As the sample thickness is increased, not only the overall intensity decreases but the temporal profile broadens and the peak occurs at later times.
为了研究散射波的统计特性, 我们跟踪了注入颗粒介质的波列在空间与时间上的强度演化.
对于每种构型, 我们通过模拟或数字高通(HP)滤波器($f \geq 300 \text{kHz}$)从传输信号中减去低频相干弹道脉冲 $E_{P}$ 和 $E_{S}$[图 2(a)], 并通过平方滤波波形的包络来确定散射波的强度.
This picture is reminiscent of the diffusively transmitted pulses of classical waves through strongly scattering random media and, in particular, the multiple acoustic scattering through a concentrated suspension of glass beads immersed in water.
However, we should stress the basic difference in the mode of wave transmission between this work and those in Ref. [8]. In our dry granular media the elastic waves propagate through the contact network from bead to bead, while in the glass bead suspensions the longitudinal waves propagate through the ambient fluid in the pores after scattering from the beads.
这不禁让人联想到经典波在强散射随机介质中的扩散传输脉冲, 特别是浸在水中的玻璃珠致密悬浮液的多重声散射.
不过, 我们应该强调的是, 这项研究与参考文献 [8] 中的研究在波的传播方式上存在根本区别. [8].在我们的干颗粒介质中, 弹性波通过接触网络在珠与珠之间传播, 而在玻璃珠悬浮液中, 纵波从珠上散射后通过孔隙中的环境流体传播.
Modeling
To ascertain the validity of the diffusion approximation, we compare the measured time profile of the average scattered intensity to the transmitted flux predicted by the scalar diffusion equation for the acoustic energy density $U$, subject to appropriate boundary conditions.
In our experimental geometry, the input face of the cylindrical sample is excited uniformly by a pistonlike source, which favors essentially the generation of the fundamental mode in this cell. As shown by Page et al. [8], the acoustic energy density measured on the axis with its source at a distance $z = L\leq W/2$ can thus be reasonably approximated by the $1$D solution to the case of a plane-wave incident on a slab geometry of thickness $L$.
为了确定扩散近似的有效性, 我们将平均散射强度的测量时间曲线与声能密度 $U$ 的标量扩散方程预测的透射通量进行了比较, 并采用了适当的边界条件.
在我们的实验几何中, 圆柱形样品的输入面被一个活塞式声源均匀激发, 这基本上有利于基模在该单元中产生. 正如 Page 等人[8]所展示的, 在距离 $z = L\leq W/2$ 处的声源轴上测量到的声能密度, 可以合理地近似为厚度为 $L$ 的板状几何体上平面波入射情况下的 $1$D 解.
Because of the low wave velocities in the granular medium and accordingly the acoustic impedance compared to that of the duralumin cell, the reflectivity $R(\theta)$ of the cell wall averaged over the incident angles $\theta$ is very high($\langle R\rangle\approx 0.95$).
For simplicity, we assume that the cell walls are perfectly reflecting at $z = 0$ and $L$. The transmitted flux into the detector is accordingly given by $J(t) = (v/4)U(L,t)$, leading to
$$ J(t) = \frac{\nu U_{0}}{2L}e^{-\frac{t}{\tau_{a}}}\sum_{n=0}^{\infty}\frac{(-1)^{n}}{\delta_{n}}\cos{\left(\frac{n\pi l^{*}}{L}\right)}e^{-\frac{D (n\pi)^{2}t}{L^{2}}} $$
where $U_{0}$ is the deposited source energy, $D = (1/3)v_{e}l^{*}$ is the diffusion coefficient with $v_{e}$ the energy transport velocity and $l^{*}$ the transport mean free path, $\tau_{a}$ is the inelastic absorption time, and $\delta_{n} = 2$ for $n = 0$, otherwise $\delta_{n} = 1$.
由于颗粒介质中的波速较低, 因此与硬铝晶胞的声阻抗相比, 细胞壁在入射角度 $\theta$ 上的平均反射率 $R(\theta)$ 非常高($\langle R\rangle\approx 0.95$).
为简单起见, 我们假设晶胞边界在 $z = 0$ 和 $L$ 处完全反射. 因此, 进入探测器的透射通量由 $J(t) = (v/4)U(L,t)$ 给出, 从而得到
$$ J(t) = \frac{\nu U_{0}}{2L}e^{-\frac{t}{\tau_{a}}}\sum_{n=0}^{\infty}\frac{(-1)^{n}}{\delta_{n}}\cos{\left(\frac{n\pi l^{*}}{L}\right)}e^{-\frac{D (n\pi)^{2}t}{L^{2}}} $$
其中, $U_{0}$ 是沉积源能量, $D = (1/3)v_{e}l^{*}$ 是扩散系数, $v_{e}$ 是能量传输速度, $l^{*}$ 是传输平均自由程, $\tau_{a}$ 是非弹性吸收时间, 当 $n = 0$ 时, $\delta_{n} = 2$, 否则, $\delta_{n} = 1$.
If we identify $v_{e}$ with a coherent wave velocity, say, the shear velocity $v_{S}$, as discussed below, we can obtain both the diffusion coefficient $D$ and the quality factor $Q(=2\pi f\tau_{a})$ by fitting the time profile of the average transmitted intensity. The solid lines in Fig. 3 are fits to the data using the solutions of Eq. (1) with a single set of fitting parameters: $D = 0.13\pm 0.01 \text{m}^{2}/\text{s}$ and $Q=200\pm 10$ for all three sample thicknesses.
The fact that a single set of parameters describes well the experimental data for all three thickness samples strongly supports the diffusion model. The slight discrepancy between the calculations and the measurements at the late time is probably due to the coupling of the granular sample with the cell wall since the wave leakage even weak into the cell wall and its radiation back to the granular sample may influence, in particular, the decay of the average transmitted intensity at the long time scale.
如果我们将 $\nu_{e}$ 与相干波速(例如剪切速度 $v_{S}$ )相提并论, 我们就可以通过拟合平均透射强度的时间曲线得到扩散系数 $D$ 和质量因子 $Q(=2\pi f\tau_{a})$. 图 3 中的实线是使用公式 (1) 的解对数据进行的拟合, 拟合参数为:对于所有三种厚度的样品, $D = 0.13\pm 0.01 \text{m}^{2}/\text{s}$, $Q = 200\pm 10$.
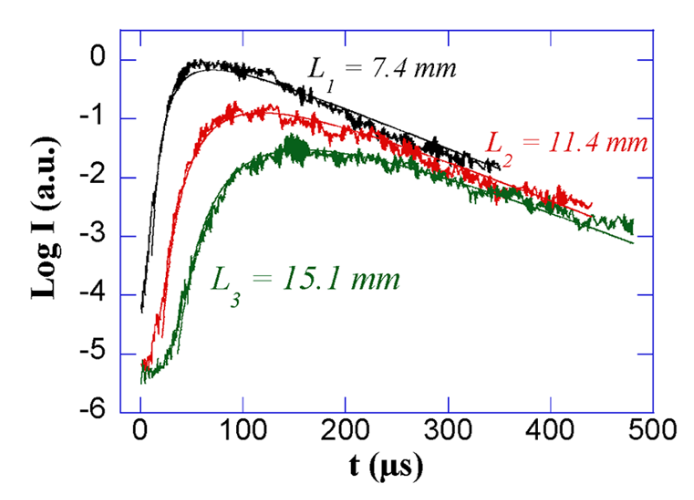
The average intensity $I$ of the scattered waves traveling across granular samples of three different thicknesses: $L = 7.4, 11.4, 15.1\text{mm}$, respectively. Theoretical curves are given by solid lines.
穿过三种不同厚度(分别为 $L=7.4、11.4、15.1\text{mm}$)颗粒样品的散射波的平均强度 $I$. 实线为理论曲线.
单组参数就能很好地描述所有三种厚度样品的实验数据, 这一事实有力地支持了扩散模型. 计算结果与后期测量结果之间的细微差别可能是由于颗粒样品与晶胞壁之间的耦合造成的, 因为即使存在微弱的波泄漏到细胞壁中并辐射回颗粒样品, 特别是影响平均透射强度在长时间尺度上的衰减.
In the above diffusion model, the vector nature of the underlying elastic wave motion in the granular medium is not explicitly taken into consideration. The relevant radiative transport equations (RTE) were derived in [10] using the first-principles calculations.
The resulting RTE are determined in terms of the power spectral densities of the fluctuations of the material density and elastic modulus and account for both shear polarizations and mode conversion between compressional and shear modes, which occurs during each scattering event.
For the range of frequency used in this study well below the first resonances of a glass sphere, e.g., the shearlike spheroidal mode: $f_{\text{res}}$
$(v_{S})_{\text{glass}}/d$$4\text{MHz}$, the granular network can be modeled as an effective random network of point masses (beads) and springs, which exhibits spatial fluctuations of both density and elastic modulus.
在上述扩散模型中, 没有明确考虑颗粒介质中基本弹性波运动的矢量性质. 相关的辐射输运方程(RTE)是参考文献[10]利用第一原理计算得出的.
由此得出的 RTE 是根据材料密度和弹性模量波动的功率谱密度确定的, 并考虑了剪切极化以及每次散射过程中发生的压缩和剪切模式之间的模式转换.
本研究中使用的频率范围远低于玻璃球的第一共振频率, 例如剪切状球面模态:$f_{\text{res}}$$(v_{S})_{\text{glass}}/d$$4\text{MHz}$, 粒状网络可被模拟为由点状质量(珠子)和弹簧组成的有效随机网络, 其密度和弹性模量均呈现空间波动.
Thus we can qualitatively interpret the features of wave transport in granular media within the framework of RTE, though the elastic RTE deduced from the firstprinciples calculation is not available for amorphouslike granular media.
The dominant energy component of the transmitted wave is at high frequency, which has a multiply scattered behavior approaching a diffusive regime. Over distances of propagation long compared to the transport mean free path, the mode conversion process leads to the complete depolarization of shear waves and randomization of the wave fields.
因此, 我们可以在 RTE 框架内定性地解释粒状介质中的波传输特征, 尽管从第一原理计算中推导出的弹性 RTE 并不适用于非晶粒状介质.
传输波的主要能量成分在高频, 具有类似扩散机制的多散射行为. 在传播距离长于传输平均自由程的情况下, 模转变过程会导致剪切波完全去极化和波场随机化.
In such a diffusion regime, the ratio $K$ of energy densities of the shear $(U_{S})$ to the compressionaltothe compressional $(U_{P})$ waves is governed by an equipartition of energy law,
$$ K = \frac{U_{S}}{U_{P}} = 2\left(\frac{v_{P}}{v_{S}}\right)^{3}. $$
The typical value of $v_{P}/v_{S}\geq \sqrt{3}$ yields $K\geq 10$, showing that in the diffusive regime the shear waves dominate in the scattered wave field, as is observed in the seismological data. Moreover, the elastic radiative transfer equation is reduced to the single diffusion equation with a diffusion coefficient approximated to that of the shear wave $D_{S} = (1/3)v_{S}l_{S}^{*}$, which confirms the applicability of the above scalar diffusion model.
在这种扩散机制中, 剪切波 $(U_{S})$ 与压缩波 $(U_{P})$ 的能量密度比 $K$ 受能量等分定律的支配:
$$ K = \frac{U_{S}}{U_{P}} = 2\left(\frac{v_{P}}{v_{S}}\right)^{3}. $$
典型值 $v_{P}/v_{S}\geq \sqrt{3}$ 得出 $K\geq 10$, 这表明在扩散机制下, 剪切波在散射波场中占主导地位, 正如在地震学数据中观察到的那样. 此外, 弹性辐射传递方程被简化为单一扩散方程, 其扩散系数近似为剪切波的扩散系数 $D_{S} = (1/3)v_{S}l_{S}^{*}$ , 这证实了上述标量扩散模型的适用性.
Material characterization
By use of the diffusion model we can infer the structure and the properties of granular materials. The transport mean free path estimated from $D$ and $v_{e}$ is $l_{S}^{*}\approx 0.87\text{mm}$(~$d$). As $l_{S}^{*}$ is the mean distance before the direction of wave propagation is randomized, it defines a length scale beyond which the scattering medium becomes statistically isotropic and homogeneous, and shall be large in comparison with the correlation length $\xi$ of the medium.
通过使用扩散模型, 我们可以推断颗粒材料的结构和性质. 根据 $D$ 和 $v_{e}$ 估算出的传输平均自由程为 $l_{S}^{*}\approx 0.87\text{mm}$(~$d$) . 由于 $l_{S}^{*}$ 是波传播方向随机化之前的平均距离, 因此它定义了一个长度尺度, 超过这个长度尺度, 散射介质在统计上就会变得各向同性和均质, 而且与介质的关联长度 $\xi$ 相比, 这个长度尺度应该很大.
The fact that $l_{S}^{*}$ is only just the grain size $d$ leads us to state that the correlation length $\xi$ of the force network in a $3$D dense granular material is short range, being of the order of the bead size. This finding is in contrast with the conjecture of a long-range correlation length of the force chains, supported by the photoelastic visualization of the stress fields in $2$D disk packings.
We believe that this contradiction resulting from the dimensionality of the system shall have a decisive effect on the topology of the contact network and accordingly the distribution of the stress field. Our results are consistent with a recent numerical simulation performed in $3$D elastic sphere packings in which a continuous transition is found from exponential to Gaussian force distribution as the applied load becomes high enough $(P > 0.75 \text{MPa})$. This crossover is associated with the spatial homogenization of the force chains.
事实上, $l_{S}^{*}$ 仅仅是晶粒尺寸 $d$, 因此我们认为三维致密颗粒材料中力网络的相关长度 $\xi$ 是短程的, 与珠子尺寸相当. 这一发现与二维圆盘填料中应力场的光弹性可视化所支持的力链长程相关长度的猜想相反.
我们认为, 由系统维度导致的这一矛盾将对接触网络的拓扑结构产生决定性影响, 并相应地影响应力场的分布. 我们的结果与最近在三维弹性球堆积中进行的数值模拟结果一致, 在该模拟中, 当施加的载荷变得足够高 $(P > 0.75 \text{MPa})$ 时, 力的分布会从指数分布连续过渡到高斯分布. 这种转变与力链的空间均质化有关.
On the other hand, measurements of scattered waves allow one to assess the high-frequency viscoelastic properties of granular media. Compared to coherent wave, the diffusing wave has the advantage of separating the absorption from the scattering attenuation. In a dense granular medium, one of the major sources of dissipation is the frictional slip of the contact forces. To study this effect, we examine the influence of a small amount of wetting liquid which lubricates the contacts between the beads.
另一方面, 通过测量散射波可以评估颗粒介质的高频时的粘-弹特性. 与相干波相比, 扩散波具有将吸收与散射衰减分开的优点. 在致密颗粒介质中, 接触力的摩擦滑移是耗散的主要来源之一. 为了研究这种效应, 我们研究了少量润湿液体对珠子间接触的润滑作用.
We mix vacuum pump oil(viscosity $\eta\approx 20\times 10^{-3}\text{Pa s}$ and surface tension $\gamma\approx 20\times 10^{-3}\text{N/m}$) with the granular sample for tens of minutes to distribute the oil uniformly among the grains. The inset of Fig. 4 illustrates a HP filtered ultrasonic signal($f\geq 300 \text{kHz}$), transmitting through a wet glass bead packing $L = 11.4\text{mm}$ with liquid volume fraction $\phi_{l}\approx 0.015$%.
For such a quantity of liquids, it was revealed that the oil is basically trapped in menisci which form at asperity on the rough surfaces of grains. Compared with the result obtained in a dry bead packing [Fig. 2(a)], a drastic effect on the wave amplitude is observed with high-frequency multiply scattered waves.
Such a highly additional dissipation of codalike scattered waves is presumably ascribed to the oilinduced lubrication, which reduces the static friction threshold between the grains and increases the number of potentially slipping contacts on the passage of shear waves.
我们将真空泵油(粘度大约是 $20\times 10^{-3}\text{Pa s}$, 表面张力大约是 $\gamma\approx 20\times 10^{-3}\text{N/m}$)与颗粒样品混合数十分钟, 使油均匀地分布在颗粒中. 图 4 的插图显示了 HP(高通) 滤波超声波信号($f\geq 300 \text{kHz}$), 该信号穿过液体的体积分数为 $\phi_{l}\approx 0.015$% 的 $L = 11.4\text{mm}$ 的湿玻璃珠堆积.
对于这种量级的液体, 研究表明, 油基本上被截留在晶粒粗糙表面的凸缘处形成的半月板(夹层)中. 与在干珠堆积中得到的结果相比[图 2(a)], 高频多重散射波对波幅产生了极大的影响.
这种对相似散射波的大量额外耗散可能是由于油的润滑作用, 它降低了晶粒之间的静摩擦阈值, 增加了剪切波通过时可能出现的滑动接触的数量.
In Fig. 4, we show for comparison the ensemble averaged acoustic intensity profiles in the dry and wet bead packings, respectively. The fit to the experimental data yields $Q_{\text{wet}} = 40 \pm 2$ and $D_{\text{wet}} = 0.15\pm 0.01\text{m}^{2}/\text{s}$ for the wet bead packing.
The low value of $Q_{\text{wet}}$ is consistent with previous absorption measurements conducted at the low-frequency range. As for the increase of $D_{\text{wet}}$ by nearly $15$% compared to the dry granular packing, it is probably related to the increasing of wave velocity of the same order of magnitude due to better bead-bead contacts caused by the lubrication effect.
在图 4 中, 我们分别展示了干珠和湿珠堆积中的系综平均声强曲线, 以作比较. 根据实验数据拟合得出, 湿珠填料的 $Q_{\text{wet}} = 40 \pm 2$, $D_{\text{wet}} = 0.15\pm 0.01\text{m}^{2}/\text{s}$.
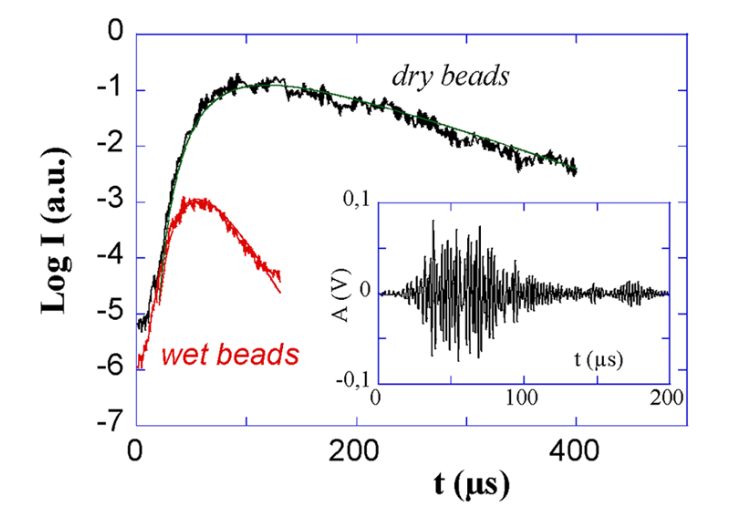
Comparison of the average intensity $I$ of the scattered waves traveling, respectively, across a dry and a wet granular packing. The solid lines are the fitting curves. The inset shows a filtered ultrasonic signal transmitting through the wet packing.
分别穿过干燥和潮湿颗粒堆积的散射波平均强度 $I$ 的比较. 实线为拟合曲线. 插图显示了经过滤波的超声波信号穿过湿堆积的情况.
$Q_{\text{wet}}$ 值较低, 这与之前在低频范围内进行的吸收测量结果一致. 至于与干颗粒填料相比, $D_{\text{wet}}$ 增加了近 15%, 这可能与润滑效应改善了珠子与珠子之间的接触而导致波速增加了相同数量级有关.
In summary, we have shown that the multiple scattering of high-frequency elastic waves through the granular force networks can be described by the diffusion approximation over a long distance of propagation $(L\gg l^{*})$. From the diffusion model we find that the correlation length $\xi$ of the force network is short range ($\xi$
$d$) in 3D granular packing under moderate stress contrary to the usual picture of long-range force correlation length ($\xi$$5-10d$)observed in a 2D granular system.A further study is to investigate the evolution of the wave transport behavior in a more tenuous granular network when the applied stress is decreased. Also with the sensitive probing by the acoustic speckles, we have measured the energy dissipation of wave in the granular medium, which allows us to highlight the crucial role of a small amount of wetting liquids on its viscoelastic properties.
总之, 我们已经证明, 高频弹性波通过颗粒力网络的多次散射可以用扩散近似来描述, 其传播距离很长 $(L\gg l^{*})$. 从扩散模型中我们发现, 在中等应力下的三维颗粒堆积中, 力网络的关联长度 $\xi$ 是短程的($\xi$$d$), 这与在二维颗粒系统中观察到的长程力相关长度($\xi$$5-10d$)的通常情况相反.
进一步的研究是调查当施加的应力减小时, 波在更脆弱的粒状网络中的传输行为的演变. 通过声学斑点的灵敏探测, 我们还测量了波在颗粒介质中的能量耗散, 这使我们能够突出少量润湿液对其粘弹性能的关键作用.
Finally, we point out the similarity of our experiment with the seismic wave propagation in the crusts of Earth and Moon.
In particular, the late-arriving coda waves in the lunar seismograms bear a striking resemblance to the multiple scattering of elastic waves in the dry granular packing. Indeed, the absence of water on the Moon causes on the upper lunar crust a highly inhomogeneous medium composed of tectonic fissures — a blocklike structure held together by the pressures due to burial.
We believe that some features revealed in our laboratory experiments may be used to explain some seismic observations in the high-frequency coda of local earthquakes in rocky soils and the granular medium may be useful as model systems for the characterization of seismic sources.
最后, 我们指出了我们的实验与地震波在地球和月球地壳中传播的相似性. 最后, 我们指出了我们的实验与地震波在地球和月球地壳中传播的相似性.
特别是, 月球地震图中晚到的尾波与干颗粒堆积中弹性波的多重散射惊人地相似. 事实上, 由于月球上没有水, 月球上部地壳是由构造裂缝组成的高度不均匀介质–这种块状结构被埋藏造成的压力固定在一起.
我们相信, 我们的实验室实验所揭示的一些特征可用来解释岩土局部地震高频尾声中的一些地震观测结果, 而颗粒介质则可作为表征震源特征的模型系统.

