Foreword
The physics of granular materials comes from an illustrious lineage. It includes names like Coulomb during the reign of Louis XVI, Faraday and Reynolds in the nineteenth century, and Bagnold, a remarkable Englishman who became enthralled by the sands of the desert, perhaps even more so than T. E. Lawrence, to the point that he resolved to understand its laws.
颗粒材料物理学有着辉煌的历史。其中包括路易十六统治时期的库仑、十九世纪的法拉第和雷诺兹,以及巴尼奥尔德,这位杰出的英国人对沙漠中的沙子着了迷,也许比 T. E. 劳伦斯还要着迷,以至于决心要了解其规律。
In spite of such great pioneers and their valiant efforts, the mechanics of powders remains largely a mystery. Even seemingly trivial questions lack clear answers. What is the weight distribution of a pile of sand dumped on the floor of an apartment under constmction? Does it depend on the way it was dumped? No one really knows.
尽管有这些伟大的先驱和他们的英勇努力,粉末的力学在很大程度上仍然是一个谜。即使是看似微不足道的问题,也缺乏明确的答案。倾倒在施工中的公寓地板上的一堆沙子的重量分布是怎样的?是否取决于倾倒的方式?没有人真正知道。
Such questions happen to be quite important in a variety of technical fields. They have applications to situations ranging from agricultural facilities storing corn in silos to the space exploration of Saturn’s rings-this “fascinating merry-go-round of rocks,” to quote Guyon and le Troadec.
这些问题在许多技术领域都非常重要。它们的应用范围很广,从在筒仓中储存玉米的农业设施到土星环的太空探索–用 Guyon 和 le Troadec 的话来说,就是 “迷人的岩石旋转木马”。
I have just mentioned two contemporary authors. They recently wrote a book entitled Le sac de billes (The bag of marbles), published in 1994 by Odile Jacob. It is a fascinating introduction to these problems, as well to somewhat unusual objects like porous materials. Yet, there is a need for a more advanced textbook for the benefit of our science students. For the last few years, Jacques Duran has taught a course in granular materials aimed at undergraduates in their senior year.
我刚才提到了两位当代作家。他们最近写了一本名为《大理石袋》(Le sac de billes)的书,1994 年由 Odile Jacob 出版。这本书是对这些问题以及多孔材料等不寻常物体的精彩介绍。然而,我们还需要一本更高级的教科书来帮助我们的理科学生。在过去几年中,Jacques Duran 教授了一门针对高年级本科生的颗粒材料课程。
He exposed them to a few general principles-for instance, the existence of many equilibrium states in the presence of friction. He was able to describe some key factors with the help of simple experiments. Or perhaps I ought to say “almost simple,” for granular media can be deceptive. A naive theoretician like myself may think that all the answers can be worked out with a couple of pounds of sand, a funnel, a few hoses, and a glass container.
他向他们介绍了一些一般原理–例如,在存在摩擦力的情况下存在许多平衡状态。他通过简单的实验描述了一些关键因素。或许我应该说 “几乎简单”,因为颗粒介质具有欺骗性。像我这样天真的理论家可能会认为,只需几磅沙子、一个漏斗、几根软管和一个玻璃容器,就能找出所有答案。
As it turns out, a thousand technical details can upset an experiment and lead to nonsensical results. The physics of granulars may not require costly hardware, but it demands enormous care. Nor is it exempt of real dangers: Industrial reactors can generate violent explosions, even when they are ostensibly empty.
事实证明,无数的技术细节都可能扰乱实验,导致不合理的结果。颗粒物理学可能不需要昂贵的硬件,但却需要非常谨慎。它也不排除真正的危险:工业反应堆即使表面上是空的,也会产生剧烈爆炸。
I am thrilled to see French physics actively engaged in the field of grains and powders, where almost everything is yet to be discovered. Within the last decade, a number of highly creative teams have popped up in places like Paris, Lyon, and Rennes. Jacques Duran leads one of those teams at the Pierre and Marie Curie University in Paris.
我很高兴看到法国物理学界积极投身于颗粒和粉末领域,在这个领域,几乎所有东西都有待发现。过去十年间,巴黎、里昂和雷恩等地涌现出了许多极富创造力的团队。雅克-杜兰(Jacques Duran)在巴黎皮埃尔和玛丽居里大学领导着其中一个团队。
This book draws on his first-rate expertise. I personally had the opportunity to read various drafts as it was taking shape. I learned a great deal from them in the process. There was a time when we had to steer anyone interested in sand to the classic text by Bagnold. From now on, Duran will be high on the required reading list. This book will fill a very real need. I sincerely wish it great success.
本书借鉴了他一流的专业知识。我本人有机会阅读了本书成型过程中的各种草稿。在这个过程中,我从中学到了很多东西。曾几何时,我们不得不引导任何对沙子感兴趣的人阅读 Bagnold 的经典著作。从现在起,Duran 将成为必读书目中的首选。这本书将满足一个非常现实的需求。我衷心祝愿它取得巨大成功。
Preface
“A body is liquid when it is divided into several smaller parts that move separately, and it is solid when all its parts are in contact.”
–Rene Descartes, Principles of Philosophy (1644-1647)
“当一个物体被分成几个单独运动的小部分时,它是液态的,而当它的所有部分都接触在一起时,它是固态的。”–勒内-笛卡尔,哲学原理(1644-1647 年)
Granular materials were probably not on Descartes’s mind when he wrote the sentence quoted above, but in some sense they might as well have been. They are indeed “divided into several smaller parts that move separately,” although they do not enjoy-far from it-the properties of a conventional liquid. And “all its parts are in contact,” although that does not confer on them the type of solidity envisioned by Descartes.
笛卡尔在写上面这句话的时候,可能并没有想到颗粒物质,但从某种意义上说,他可能想到了。它们的确 “被分成几个小的部分,分别运动”,尽管它们并不享有–远远不是–传统液体的特性。而且,“它的所有部分都是接触的”,尽管这并没有赋予它们笛卡尔所设想的那种坚固性。
This ambiguity illustrates well the lack of understanding, which has persisted until quite recently, of the properties of granular media, in spite of their prevalence not only in nature but in many human endeavors as well. Recent progress in several different areas of physics has fostered a critical reassessment of the concepts passed on to us by the scientists and engineers of generations past. As a result, a number of research groups dedicated to working on granular materials have sprouted all over the world in the last decade. They have produced a harvest of experimental observations, numerical simulations, novel concepts, and theoretical models.
尽管颗粒介质不仅存在于自然界,也存在于人类的许多活动中,但直到最近,人们对颗粒介质的特性仍然缺乏了解。物理学多个不同领域的最新进展促进了对过去几代科学家和工程师传授给我们的概念进行批判性的重新评估。因此,在过去的十年中,世界各地涌现出了许多致力于研究颗粒材料的研究小组。他们在实验观察、数值模拟、新概念和理论模型方面取得了丰硕成果。
Faced with such an onslaught of new facts, a newcomer to the field is likely to feel a bit overwhelmed. To make matters worse, this growing area of science has yet to benefit from any standardization, even in matters of terminology. I myself came to that realization while collecting material to teach an advanced course in the physics of liquids. The purpose of this text is to provide a smoother introduction to this exciting new area of research. Meant primarily as a teaching vehicle, it should answer the needs of fourth-year college students, researchers just entering the field, and young engineers interested in process engineering dealing with granular materials.
面对纷至沓来的新知识,初涉这一领域的人很可能会感到不知所措。更糟糕的是,这一不断发展的科学领域尚未从任何标准化中受益,甚至在术语方面也是如此。我自己就是在收集材料以教授液体物理学高级课程时认识到这一点的。这本教材的目的是为这一令人兴奋的新研究领域提供更顺畅的介绍。它主要是作为一种教学工具,应能满足大学四年级学生、刚刚进入该领域的研究人员以及对处理颗粒材料的过程工程感兴趣的年轻工程师的需要。
More generally, it is aimed at anyone with a sufficient theoretical basis who is interested in learning how to start from quite simple experiments and, from there, build up concepts and theories about a medium whose behavior is most often surprising and counterintuitive. My goal has been to gather, in as self-contained a manner as possible and in a unified language, the background necessary to understand the latest developments, as well as to present the rudiments of granular physics.
更广泛地说,这本书面向任何有足够理论基础的人,他们有兴趣学习如何从非常简单的实验入手,并在此基础上建立有关介质的概念和理论,而介质的行为往往是令人惊讶和违反直觉的。我的目标是以尽可能自足的方式和统一的语言,收集理解最新发展所需的背景知识,并介绍颗粒物理学的基本原理。
Given the current status of this young discipline, any progress is likely to come from experiments. Henri Poincare once said: “It has been quite some time since anyone has thought of getting ahead of experimentation or to construct the world on the basis of a few hasty hypotheses.” The remark is particularly relevant to the physics of granular media. This book is rooted in that very principle. In this spirit, it contains many descriptions of experimental devices and accounts of experimental results obtained under conditions that are as controlled as possible.
鉴于这门年轻学科的现状,任何进展都可能来自实验。Henri Poincare 曾经说过"已经有相当长的一段时间,没有人想过要走在实验的前面,也没有人想过要根据一些草率的假设来构建世界"。这句话尤其适用于颗粒介质物理学。本书正是根植于这一原则。本着这一精神,书中包含了许多实验装置的描述,以及在尽可能可控的条件下获得的实验结果的介绍。
These provide the backdrop for concepts, models, and ideas that are pushed to levels that some might find too speculative. The adopted strategy, whose limitations must be borne in mind, goes with the very nature of this discipline, which is still very much in its infancy. In this context, this book discusses concepts and results as they are known to us at the present moment. As such, it is only a snapshot, as our understanding of this topic is bound to evolve, perhaps even undergo major revisions.
这些都为概念、模型和想法提供了背景,这些概念、模型和想法被推到了一些人可能会认为过于投机的高度。本书所采取的策略与这门仍处于起步阶段的学科的性质相吻合,但必须牢记其局限性。因此,本书讨论的是我们目前已知的概念和结果。因此,它只是一个缩影,因为我们对这一主题的理解必然会不断发展,甚至可能会进行重大修订。
Lest it become a dry compilation of facts, writing a book of this kind entails somewhat arbitrary choices that remain the sole responsibility of the author. On more than one occasion, I felt compelled to leave out this particular result or that, even though I may come to regret it in the future. I did so simply because it did not readily fit in with the flow of the presentation or because it would have taken me too far afield.
为了避免本书成为一本枯燥的事实汇编,在撰写这类书籍时,作者必须做出一些武断的选择。有不止一次,我感到不得不省略这个或那个特例,尽管将来可能会后悔。我这样做的原因很简单,因为它不容易与讲述的流程相吻合,或者因为它会把我带得太远。
I beg for those whose work is mentioned too cursorily or not at all to forgive me. This by no means implies a negative judgment on my part. My choice was guided exclusively by pedagogical concerns and my own concept of the logical flow of the material. My decisions were often agonizingly difficult.
我恳请那些其工作被提及得极其草率或根本没有被提及的人原谅我。这绝不意味着我对他们的工作做出了负面评价。我的选择完全是出于教学上的考虑和我自己对素材逻辑流程的理解。我的决定常常是痛苦而艰难的。
My thanks go to my colleagues and friends in my own laboratory (Eric Clement, Jean Rajchenbach, and Touria Mazozi). I am also grateful to the members of the Physics of Heterogeneous and Complex Matter Research Group affiliated with the National Center of Scientific Research (CNRS) and with the European HCM (Human Capital and Mobility) Network.
我还要感谢我自己实验室的同事和朋友(Eric Clement、Jean Rajchenbach 和 Touria Mazozi)。我还要感谢隶属于国家科学研究中心(CNRS)的异质和复杂物质物理学研究小组以及欧洲人力资本和流动性(HCM)网络的成员。
I am enormously indebted to them not only for much of the technical material in the book but also for infusing in it their irrepressible enthusiasm which I hope will brighten the experience of the reader. I acknowledge the careful reading of the french manuscript and comments by Ko Okumura and VJ.-P. Faroux. Axel Reiseinger successfully carried out the translation from the French edition. He kept within the spirit of the text while suggesting numerous improvements and clarifications.
我非常感谢他们,他们不仅在书中提供了许多技术材料,而且还在书中倾注了他们难以抑制的热情,我希望这将为读者带来光明的阅读体验。我感谢 Ko Okumura 和 VJ.-P. Faroux 对法文手稿的仔细阅读和评论。Faroux.Axel Reiseinger 成功地完成了法文版的翻译工作。他在保持文本精神的同时,提出了许多改进和澄清的建议。
Finally, I owe a large debt of gratitude to Pierre-Gilles de Gennes and Etienne Guyon, both of whom played an instrumental role in the early stages of the research discussed here. I was fortunate to have their unrelenting support and encouragement to write and publish the material in this book. It borrows a great deal from their own work.
最后,我非常感谢皮埃尔-吉勒-德-热内(Pierre-Gilles de Gennes)和艾蒂安-居庸(Etienne Guyon),他们两人在本书所讨论的研究的早期阶段发挥了重要作用。我很幸运能得到他们不懈的支持和鼓励,撰写并出版了本书中的资料。本书在很大程度上借鉴了他们的研究成果。
1 Introduction
1.1 Some Orders of Magnitude Defining the Problem
The physics of granular materials deals primarily with macroscopic objects. The term “macroscopic” means here that the objects making up such materials must at the very least be visible to the naked eye. This is in contrast to mesoscopic or microscopic media.
As it turns out, the very concept of granular material imposes some further restrictions, raising the low end of the range somewhat above the limits of our visual acuity. It is important to realize from the outset that the physics of such objects has in most cases nothing whatsoever to do with the notion of temperature, at least not as we normally understand it.
颗粒材料物理学主要涉及宏观物体。这里所说的 “宏观” 是指构成这些材料的物体至少必须是肉眼可见的。这与介观或微观介质截然不同。
事实证明,颗粒物质的概念本身就施加了一些进一步的限制,使其范围下限略高于我们视力极限。我们必须从一开始就认识到,在大多数情况下,这类物体的物理学原理与温度概念毫无关系,至少不是我们通常所理解的那样。
To appreciate this, we need only calculate the kinetic energy $E_{k}$ of a small bead of silicate glass-a basic component of river sand. As we will see shortly, the physics of dry granular materials of the type we are interested in involves objects that are typically $100$ microns ($\mu\text{m}$) in size or larger. For typical translation velocities of the order $1\text{ cm/s}$, we find that $E_{k} = \frac{1}{2}mv^{2}\approx 10^{-12}$ Joule. If this kinetic energy were due entirely to thermal agitation, it would correspond to a temperature of $10^{11}\text{ K}$!
要理解这一点,我们只需计算一小粒硅酸盐玻璃珠(河沙的基本成分)的动能 $E_{k}$。我们很快就会看到,我们感兴趣的这种干燥颗粒物料的物理学涉及的物体通常大小为 $100$ 微米($\mu\text{m}$)或更大。对于 $1 \text{cm/s}$ 数量级的典型平移速度,我们发现 $E_{k} = \frac{1}{2}mv^{2}\approx 10^{-12}$ 焦耳。如果这种动能完全是由热运动产生的,那么它对应的温度就是 $10^{11}\text{ K}$!
Furthermore, the loss $\Delta E_{p}$ of potential energy experienced by such a particle, as it drops by a height equal to its own diameter $d$, is given by $\Delta E_{p} = mgd$ (this corresponds to a situation where particles slide down past each other while remaining in contact). We find that $\Delta E_{p}$ and $E_{k}$ are roughly equal.
此外,当粒子下降的高度等于其自身直径 $d$ 时,它所经历的势能损失 $\Delta E_{p}$ 由 $\Delta E_{p} = mgd$ 给出(这相当于粒子在保持接触的情况下从彼此身边滑过)。我们发现 $\Delta E_{p}$ 和 $E_{k}$ 大致相等。
The conclusion is that the collective behavior of such a granular medium simply cannot be described in terms of traditional Brownian motion. Some other mechanism responsible for generating fluctuations is required if we insist on defining a temperature of some kind. We will encounter many such examples in the course of this book. Incidentally, it is instructive to calculate what the diameter of a particle of this same material should be if it is to be the seat of any significant thermal agitation at ordinary temperature (in the sense of $E_{k}\approx kT$).
结论是,这种颗粒介质的集体行为根本无法用传统的布朗运动来描述。如果我们坚持要定义某种温度,就需要有其他机制来产生涨落(Fluctuation)。在本书的学习过程中,我们会遇到很多这样的例子。顺便提一下,如果要在常温下(在 $E_{k}\approx kT$ 的意义上)对这种材料的颗粒进行任何显著的热运动,那么计算一下这种颗粒的直径应该是多少是很有启发的。
The result is about $1 \mu\text{m}$, or some two orders of magnitude smaller than the size of the smallest particles of interest here. This one observation alone constitutes a serious obstacle to modeling the properties of granular piles by means of conventional thermal or hydrodynamic variables. Except in a few very special cases, it is clear that the behavior of granular materials will be determined primarily by the more or less preferential and collective displacement of the particles involved.
结果约为 $1 \mu\text{m}$,或者比这里所关注颗粒的最小尺寸都还小两个数量级。仅这一个观察结果, 就已经严重阻碍了用传统的热力学变量或流体力学变量来模拟颗粒堆的特性。除少数非常特殊的情况外,颗粒材料的行为显然主要由相关颗粒或多或少的优先和集体位移决定。
The fact that Brownian motion is inconsequential explains why granular materials almost invariably resist any attempt at mixing. As we will see, shaking a collection of grains typically results in segregation, in other words, in separation according to size, precisely the opposite to what is being sought.
By contrast, it is well known that in liquids, Brownian motion is the key mechanism responsible for intimate mixing of the various components. The phenomenon of granular segregation can be viewed as further evidence of the lack of thermal agitation with a mean free path characteristic of the average distance between particles.
布朗运动无足轻重这一事实解释了为什么颗粒材料几乎总是反抗任何(将其)混合的尝试。正如我们将看到的那样,摇晃颗粒集合体通常会导致分离,换句话说,根据大小进行分离,而这恰恰与我们所追求的相反。
与此相反,众所周知,在液体中,布朗运动是各种成分亲密混合的关键机制。颗粒分离现象可被视为缺乏热运动的进一步证据,其平均自由程的特点是颗粒之间的平均距离。
Both nature and industry make heavy use of a variety of granular materials covering an extremely broad range of shapes, sizes, micromechanical, and chemical properties. In Chapter 2, we will mention a standard classification scheme based on size, but we will not concern ourselves with shapes, nor will we discuss the distribution laws of dissimilar media and associated measurement or identification techniques.
Readers interested in such issues are referred elsewhere. What we will do is try to highlight the fundamental principles governing the physics of these materials, and to that end we will focus on simple and well-characterized objects. For reasons that will become clear later on, we will restrict our attention almost exclusively to the physical properties and behavior of so-called dry granular materials.
自然界和工业界都大量涉及各种颗粒材料,其形状、大小、微机械和化学性质的范围极为广泛。在第 2 章中,我们将提到基于颗粒尺度的标准分类方案,但不会涉及颗粒形状,也不会讨论不同介质的分布规律以及相关的测量或识别技术。
对这些问题感兴趣的读者可到另行查阅。我们所要做的是努力突出这些材料的物理学基本原理,为此,我们将把重点放在简单和特性良好的物体上。由于稍后会明确的原因,我们将几乎只关注所谓干燥颗粒材料的物理性质和行为。
Granted, a number of concepts that will come up during the course of this book can, with some precautions, apply to more complicated objects, such as pastes, muds, and other concentrated mixtures, in which particles interact with an ambient fluid. Be that as it may, we will largely confine our study to particles with idealized shapes (generally spherical or cylindrical) and whose micromechanical properties are well understood.
当然,在本书的研究过程中会出现的一些概念,在采取一些预防措施的情况下,也适用于更复杂的物体,如糊状物、泥浆和其他浓缩混合物,在这些物体中,颗粒与环境流体相互作用。尽管如此,我们的研究仍将主要局限于具有理想化形状(一般为球形或圆柱形)且微机械特性已被充分理解的颗粒。
In order to convince the reader that granulars present a serious challenge both from an economic perspective and on a more fundamental physics level, we shall briefly review a few practical applications of these materials as well as some basic problems which we will examine in more detail in later chapters.
In a somewhat different vein-of considerable importance to human affairs, we might add-granulars of various degrees of complexity are at the heart of the geophysical sciences.
In fairness, geophysicists have often beaten “conventional” physicists in defining many of the concepts to be discussed in these pages.
为了让读者相信,无论是从经济角度还是从更基础的物理学角度来看,颗粒材料都是一个严峻的挑战,我们将简要回顾一下这些材料的一些实际应用以及一些基本问题,我们将在后面的章节中对这些问题进行更详细的研究。
与此略有不同的是,不同复杂程度的颗粒物质是地球物理科学的核心。
平心而论,地球物理学家在定义本文将要讨论的许多概念时,往往胜过 “传统” 物理学家。
The physical laws governing the behavior of granular media actually apply to objects whose dimensions cover several orders of magnitude. From grains, a few hundred microns each, to ice floes drifting across the polar seas (over distances of $1000\text{ km}$), not forgetting Saturn’s rings (made of icy particles about $1\text{ cm}$ wide distributed in a band roughly $1\text{ km}$ thick), the science of granulars covers at least twelve decades of sizes.
支配颗粒介质行为的物理定律, 实际上可适用于尺寸覆盖几个数量级的物体。从每粒只有几百微米的颗粒,到漂流在极地海洋上的浮冰(距离达 $1000\text{ km}$),更不用说土星环(由宽约 $1\text{ cm}$ 的冰颗粒组成,分布在大约 $1\text{ km}$ 厚的条带中),颗粒科学跨越了至少十二个十年的尺度。
The fact that aggregates seem to obey universal laws applicable over such a wide range of dimensions and characteristics is a strong incentive to pursue fundamental studies in that area.
For instance, phenomena of segregation and intermittent blockages are pervasive in numerous industrial processes involving granular materials.
(颗粒)集合体似乎遵循适用于如此广泛的维度和特征的普遍规律,这一事实有力地推动了该领域的基础研究。
例如,分离和间歇性堵塞现象在许多涉及颗粒材料的工业流程中普遍存在。
Accordingly, the remainder of this chapter will be devoted to a brief and selective review of a few techniques and processes that in one way or another are subject to phenomena such as convection, segregation, blockages by arching, all of which are routinely encountered in industry. These effects will be examined in greater depth in subsequent chapters.
因此,本章的其余部分将用于简要和有选择性地回顾一些技术和工艺,这些技术和工艺在某种程度上受到对流、分离、桥型堵塞等现象的影响,所有这些现象都是工业中经常遇到的。这些影响将在后续章节中进行更深入的探讨。
1.2 Economic Implications and Industrial Problems
As we have already pointed out, granular materials occupy a prominent place in our culture. The worldwide annual production of grains and aggregates of various kinds is gigantic, reaching approximately ten billion metric tons. Coal accounts for about 3.5 billion tons ofthat total, cements and ordinary construction materials for one billion tons, to which we can add equal amounts of sand and gravel.
These constitute what is generally referred to as low-cost raw materials. The processing of granular media and aggregates consumes roughly $10$% of all the energy produced on this planet. As it turns out, this class of materials ranks second, immediately behind water, on the scale of priorities of human activity. As such, any advance in understanding the physics of granulars is bound to have a major economic impact.
正如我们已经指出的,颗粒材料在我们的文明中占有重要地位。全世界谷物和各种集料的年产量巨大,约达 $100$ 亿吨。其中,煤炭约占 $35$ 亿吨,水泥和普通建筑材料约占 $10$ 亿吨,此外,我们还可以加上等量的沙子和砾石。
这些就是通常所说的低成本原料。颗粒介质和集料的加工消耗了地球上生产的所有能源中的大约 $10$%。事实证明,这一类材料在人类活动的优先级中排名第二,仅次于水。因此,在了解颗粒物理学方面取得的任何进展都必然会对经济产生重大影响。
The industrial technology used in the treatment of granular materials involves a number of processes. First comes the extraction of ores, sands, and gravel, which often relies on dredging. Next comes crushing and grinding, followed by separation, all of which are commonly used with low-value-added materials.
Since raw materials often account for more than $85$% of the total cost, it is easy to understand why so little effort has been expended to improve the basic technology, which often dates back to the nineteenth century.
用于处理颗粒材料的工业技术涉及多个流程。首先是矿石、砂和砾石的提取,这通常依赖于挖泥。接着是破碎和研磨,然后是分离,所有这些通常都用于低增值材料。
由于原材料通常占总成本的 $85$% 以上,这就不难理解为什么在改进基本技术方面所做的努力如此之少,而这些技术通常可以追溯到十九世纪。
Not much has been optimized, despite the fact that methods of transport (fluidized beds, conveyor belts), storage (silos), and mixing (e.g., cement trucks) figure in all stages of the industrial processing of aggregates. Problems have received primitive solutions at best.
The more specialized and developed arena of high-value-added materials include the cosmetic and pharmaceutical industries, specialized chemistry, and the food industry, which demand increasingly sophisticated processing technologies.
尽管运输(流化床、传送带)、储存(筒仓)和混合(如水泥车)方法在集料工业加工的各个阶段都有应用,但优化的程度并不高。这些问题充其量只能得到最原始的解决方案。
高增值材料的应用领域更加专业和发达,包括化妆品和制药业、特种化学和食品工业,这些行业对加工技术的要求越来越高。
1.2.1 Industrial Processing of Granulars
Construction Materials
The construction industry (housing, hydraulic concrete needs, public works projects, and so on) consumes aggregates at the rate of seven tons per capita per year, which generated revenues of some fifteen billion francs (three billion dollars) in 1994.
建筑业(住房、水工混凝土需求、公共工程项目等)每年人均消耗 $7$ 吨集料,1994 年的收入约为 $150$ 亿法郎($30$ 亿美元)。
Next to water, aggregates are the most heavily used material. Natural aggregates are of alluvial, volcanic, or sedimentary origin.
After being extracted from quarries or underwater deposits, they go through a series of steps that require the handling of huge quantities of material in granular form.
Among these operations are short-distance conveying (often by forced flow through pipes), scalping (i.e., the separation of nonvaluable fine residues, which removes at least part of the problem for subsequent processing), crushing and grinding, followed by sifting, washing, hydrocycloning, and desliming (particularly to improve the properties of sand and gravel).
除水之外,聚集体(集料, Aggregates)是使用量最大的材料。天然集料来源于冲积、火山或沉积。
从采石场或水下矿床开采出来后,它们需要经过一系列步骤,处理大量的颗粒状材料。
这些操作包括短距离输送(通常是通过管道强制流动)、筛除(即分离出无价值的细小残留物,这至少为后续加工消除了部分问题)、破碎和研磨,然后是筛分、清洗、水力旋流器和脱硅(特别是为了改善砂石的特性)。
筛除(Scalping)是指的从混合物中剔除不符合特定尺寸或质量要求的颗粒, 筛分(Sifting)是指的不仅有不合格颗粒的剔除, 还通常包含着对颗粒混合体的分级(按粒度进行分类/分组)
The sequence generally ends with storage and ultimately transportation to the point of use. Most of these operations suffer from a troublesome list of disruptive phenomena such as flow obstructions, formation of plugs, and segregation, all of which we will have an opportunity to analyze in detail later on.
这一系列过程一般以储存和最终运输到使用地点结束。在这些操作过程中,大多数都会出现一系列令人头疼的干扰现象,如流动受阻、形成堵塞和偏析等,我们稍后将有机会对所有这些现象进行详细分析。
Industrial requirements are so diverse, and the properties of the corresponding materials so complex, that it takes no fewer than $15$ parameters to fully specify an aggregate used, for instance, in the preparation of hydraulic concretes.
They describe a menu of characteristics like thickness, cleanliness, degree of crushing, cohesion, coefficient of flatness, and a host of others.
This proliferation of empirical coefficients attests to the inherent complexity of the industrial world, while physicists try to reduce them to no more than two or three fundamental micromechanical parameters, perhaps because that is the most they can handle.
工业要求多种多样,相应材料的特性也非常复杂,因此,要完全确定一种聚集体(例如,用于制备水工混凝土的聚集体),至少需要 $15$ 个参数。
这些参数描述了厚度、清洁度、破碎程度、内聚力、平整度系数等一系列特性。
经验系数的激增证明了工业世界固有的复杂性,而物理学家却试图将其减少到不超过两三个基本的微观机械参数,也许这就是他们所能处理的最多的参数。
It would seem that physics has a long way to go to catch up with the real world. Yet-and this is a very encouraging sign-the troublesome phenomena that plague industrial processes out in the field (blockages, arches, segregation) show up readily even in our idealized theoretical models. In this regard, it is instructive to at least briefly discuss some problems associated with the concrete industry.
看来,物理学要赶上现实世界还有很长的路要走。然而–这是一个非常令人鼓舞的迹象–即使在我们理想化的理论模型中,困扰现场工业过程的麻烦现象(堵塞、拱起、分离)也会轻易出现。在这方面,至少简要讨论一下与混凝土工业相关的一些问题是很有启发性的。
Paradoxically, how aggregates contribute to the strength of concrete was rediscovered only very recently. It has only been a few years since the resilience of bituminous or high-performance concretes was proven to be due in large part to the characteristics of the aggregates used in their manufacture. Everyone knows that concrete is essentially a mixture of aggregates and cement, and that it undergoes a slow chemical transformation (on a scale of tens of years).
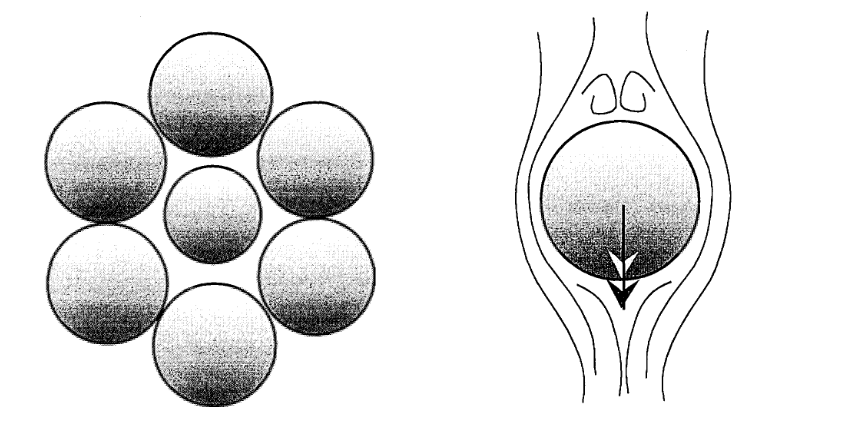
Since it is a composite material, the key to success is to minimize the influence of the more fragile binder material, and maximize that of the much stronger granular material in its midst. The practical solution is embodied in hypercompact arrangements, which constitute a natural answer to the problem posed many centuries ago by Appolonius of Perga (ca. 262, ca. 190 B.C.). It is illustrated in Figure 1.
自相矛盾的是,集料对混凝土强度的贡献直到最近才被重新发现。沥青混凝土或高性能混凝土的回弹性被证明在很大程度上归功于其制造过程中使用的集料特性,而这只是几年前的事。众所周知,混凝土本质上是集料和水泥的混合物,它经历着缓慢的化学变化(以数十年为单位)。
由于它是一种复合材料,成功的关键在于最大限度地减少较脆弱的粘合剂材料的影响,同时最大限度地增加其中更坚固的颗粒材料的影响。超紧凑排列就是实际解决方案的体现,它是对佩尔加的阿波洛尼乌斯(Appolonius of Perga,约公元前 262 年至约公元前 190 年)在许多世纪前提出的问题的自然解答。如图 1 所示。
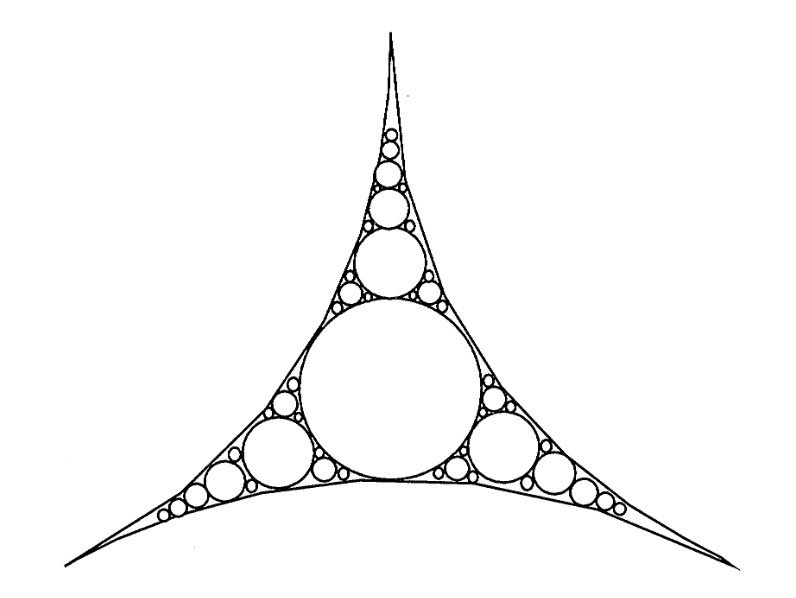
Around 200 B.C., Appolonius of Perga invented the arrangement shown here to tile a surface as fully as possible with circles of various sizes. This object enjoys the property of self-similarity.
大约在公元前 200 年,佩尔加的阿波洛尼乌斯(Appolonius of Perga)发明了这里所示的排列方式,用不同大小的圆尽可能完整地铺贴一个表面。这个物体具有自相似性。
This idea is probably what inspired engineers to add granulars of various sizes, spanning several orders of magnitude, to the mixtures they prepare to make highstrength concretes. The finest ingredients in these mixtures are of submicron size; they are called silica fume.
Their cost is extremely high, but they have made it possible to produce concretes which such high strength that the construction of skyscrapers a full kilometer high has become technologically feasible. Indeed, the city of Tokyo is planning to erect just such structures.
Nevertheless, it is not difficult to anticipate the enormous problems encountered when trying to mix such a granular medium compactly, given the unavoidable phenomenon of size segregation.
这种想法可能就是工程师们在配制高强度混凝土的混合物中添加不同大小(跨越几个数量级)颗粒的灵感来源。这些混合物中最细的成分为亚微米级,被称为硅灰。
它们的成本极高,但却能生产出强度极高的混凝土,以至于在技术上可以建造整整一公里高的摩天大楼。事实上,东京市正在计划建造这样的建筑。
尽管如此,考虑到不可避免的颗粒尺度分离现象,不难预料在试图将这种颗粒介质混合致密时, 会遇到的巨大问题。
It is only fitting to acknowledge that, although they were not familiar with the dauntingly complex physics involved, engineers and specialists in the fields of concretes and aggregates have proven remarkably adept at building on their rich experience and mastering the difficult art of devising fluid binders in which each grain can find its ideal spot.
我们必须承认,尽管混凝土和集料领域的工程师和专家并不熟悉其中所涉及的令人生畏的复杂物理学,但事实证明,他们非常善于利用自己的丰富经验,掌握了设计流体粘结剂的高难度艺术,使每颗晶粒都能在其中找到自己的理想位置。
No one can deny that systematic experimentation has yielded the right answers, even though manufacturing costs are so high that applications are for the time being restricted to the construction of highly specialized buildings. It is reasonable to expect that the possible contributions of physics to a better understanding of the properties of construction materials may substantially lower the costs of producing, conveying, and mixing them. These processes are intimately related to problems of flow and segregation, which are to be taken up in Sections 1.2.2 and 1.2.3.
尽管制造成本如此之高,以至于其应用目前仅限于建造高度特化的建筑物,但没有人能够否认,系统的实验已经得出了正确的答案。我们有理由期待,物理学在更好地理解建筑材料特性方面可能做出的贡献,可能会大大降低生产、输送和混合这些材料的成本。这些过程与第 1.2.2 节和第 1.2.3 节将要讨论的流动和分离问题密切相关。
We will refrain from treating here the principles of soil mechanics, which fall largely in the domain of geophysics and geology, or the kinds of problems civil engineers have long been accustomed to dealing with. There exist in this area numerous models painstakingly put together, and with a respectable track record.
在这里,我们将不讨论土壤力学原理,因为这主要属于地球物理学和地质学的范畴,也不涉及土木工程师长期以来习惯于处理的各类问题。在这一领域,有许多模型都是经过精心设计的,而且有着令人尊敬的记录。
For instance, most soil-mechanics engineers tend to view granular materials as continuous objects that obey the usual laws of classical mechanics (including friction, stress-strain relations, plastic deformation, and the like), such as they apply to homogeneous solids. As we will see, there are cases when this approach raises serious questions.
例如,大多数土壤力学工程师倾向于将颗粒材料视为连续的物体,它们遵守经典力学的通常定律(包括摩擦、应力-应变关系、塑性变形等),如适用于均质固体的定律。正如我们将要看到的,在某些情况下,这种方法会引发严重的问题。
From a practical point of view, however, it does offer the advantage of permitting simple calculations to predict the behavior of various structures made of granular materials, such as roadways, with generally adequate safety margins.
不过,从实用的角度来看,它的优势在于可以通过简单的计算来预测由颗粒材料制成的各种结构(如道路)的行为,而且一般都有足够的安全裕度。
There is, however, one related phenomenon that deserves to be singled out, because it shows up routinely in everyday life. We are referring to segregation by shearing, an effect that is characteristic of most granular materials. Figure 2 describes the phenomenon in question, which civil engineers are quite familiar with. They have to contend with it as they plan and manage construction projects.
不过,有一种相关现象值得特别指出,因为它在日常生活中经常出现。我们指的是剪切离析,这是大多数颗粒材料都会产生的一种效应。图 2 描述了土木工程师非常熟悉的这种现象。土木工程师在规划和管理建筑项目时必须面对这种现象。

Grading the embankment on the side of a road with a bulldozer causes segregation by shearing. The concentration of large rocks is much greater on the suti’ace of the embankment than in the interior.
用推土机平整路边的路堤会造成剪切离析。大块岩石在路堤底部的集中程度远高于内部。
Processing Industries
Generally speaking, modern manufacturing methods of high-technology materials rely heavily on the processing of granular materials. We are not about to review each of the many applications, transformations, and various processes involving granulars at some stage of the technology.
One book would not be enough to cover them all. We will simply give a few examples selected for the purpose of highlighting the many-faceted problems faced by industry, and their connections with the fundamental approach advocated in this book.
一般来说,高科技材料的现代制造方法在很大程度上依赖于颗粒材料的加工。我们不打算逐一回顾颗粒材料在某一技术阶段的众多应用、转化和各种工艺。
一本书不足以涵盖所有问题。我们仅举几个例子,以突出工业面临的多方面问题,以及这些问题与本书所倡导的基本方法之间的联系。
We start by making a clear distinction between two separate branches of the chemical industry. On the one hand are industries that typically deal with large quantities of materials in granular or powder form. Their problems are generally similar to the ones we have already mentioned, such as transport through pipes, storage, or granular segregation. On the other hand are the chemical or pharmaceutical industries where materials are prepared in relatively small quantities, but with high-value-added materials.
我们首先要明确区分化工行业的两个不同分支。一方面是通常处理大量颗粒状或粉末状材料的行业。它们的问题通常与我们已经提到的问题类似,如管道运输、储存或颗粒离析。另一方面是化工或制药行业,这些行业制备的材料数量相对较少,但都是高增值材料。
In this case, the demands in terms of purity and reproducibility are obviously far more stringent. Accordingly, their manufacturing technology tends to be much more sophisticated. In this context, we will shortly discuss a technique designed to get around-to the greatest extent possible-the phenomenon of granular segregation.
在这种情况下,对纯度和可重复性的要求显然要严格得多。因此,它们的制造技术往往要复杂得多。在这种情况下,我们很快就会讨论一种旨在最大限度地避免颗粒离析现象的技术。
An Example: Casting by Sacrificial Polystyrene
The technique discussed here has been used recently by the French automobile maker Peugeot to produce engine blocks which would have been extremely difficult to manufacture any other way.
A number of electromechanical firms and steel foundries have studied and developed similar processes. In principle, the method, illustrated in Figure 3, is quite simple and of potentially low cost.
Unfortunately, its practical implementation runs into difficult problems because of a fundamental property of granular materials, which we will examine in detail in Chapter 3, known as convection by vibration.
最近,法国汽车制造商标致(Peugeot)就采用了这里讨论的技术,生产出了极其难以用其他方法制造的发动机缸体。
一些机电公司和钢铁铸造厂已经研究并开发了类似的工艺。原则上,图 3 所示的方法非常简单,而且成本可能很低。
遗憾的是,由于颗粒材料的一个基本特性(我们将在第 3 章中详细研究),即振动对流,它在实际应用中遇到了困难。
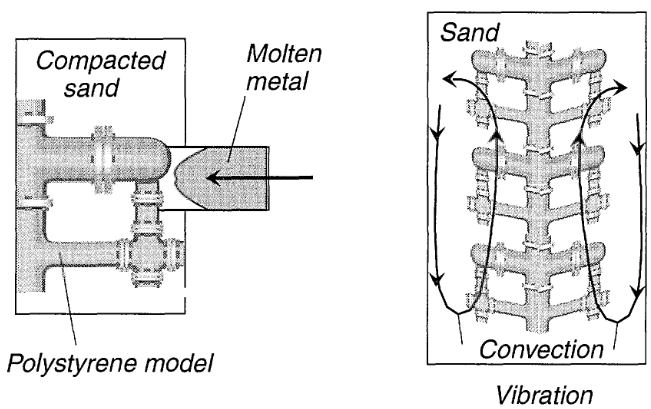
Principle of casting by sacrificial polystyrene. The right-hand drawing shows an industrial application of the principle. Several molds are placed in a container filled with compacted sand. Granular convection phenomena in the sand can cause the structure to deform prior to casting, resulting in a large number of rejects.
牺牲聚苯乙烯铸造原理。右图展示了该原理的工业应用。几个模具被放置在一个装满压实砂的容器中。砂中的颗粒对流现象会导致结构在浇铸前变形,从而产生大量废品。
The sequence of steps required in this technique is as follows:
- A polystyrene model of the object to be duplicated in metal form is prepared.
- The model is placed inside a container that is filled with fine sand.
- The whole system is shaken vigorously by means of a vibrating support placed under the container.
- At the conclusion of this step, the sand occupies every bit of space between the model and the container’s wall. Highly compacted, it is now ready to act as the mold.
- Molten metal is poured through an opening connected to the polystyrene model. The polystyrene instantly vaporizes away, leaving in its place the liquid metal which solidifies into the appropriate shape.
该技术所需的步骤顺序如下:
- 准备一个聚苯乙烯模型,用于复制金属形式的对象。
- 将模型放置在一个装满细沙的容器内。
- 通过放置在容器下方的振动支撑,使整个系统剧烈震动。
- 在这一步骤结束时,沙子占据了模型和容器壁之间的每一个空间。经过高度压实,它现在已经准备好作为模具。
- 熔融金属通过与聚苯乙烯模型相连的开口倾倒。聚苯乙烯立即蒸发,留下液态金属,金属凝固成适当的形状。
In principle, the technique ought to produce nearly perfect results. One of its advantages is that it eliminates the burrs formed at the joints between separate sections of conventional molds. Unfortunately, during the shaking process, granular convection gives rise to a powerful central flux of sand which has a disturbing tendency to deform-and sometimes to destroy outright-the polystyrene model. This is a very serious problem that affects about $90$% of the products, causing a flood of rejects.
原则上,这种技术应该能产生近乎完美的效果。其优点之一是消除了传统模具各部分之间接缝处形成的毛刺。遗憾的是,在摇动过程中,颗粒对流会产生强大的中心砂流,这种砂流有一种令人不安的趋势,会使聚苯乙烯模型变形,有时甚至会完全破坏。这是一个非常严重的问题,影响到大约 $90$% 的产品,造成大量废品。
This problem is quite typical in the physics of granular materials. The solution is relatively straightforward: Convection can be largely eliminated by using nearly frictionless containers and granulars. But this ignores the fact that convection also plays a useful role, as it promotes the filling of every nook and cranny around the model.
这个问题在颗粒材料物理学中非常典型。解决方法相对简单:通过使用几乎无摩擦的容器和颗粒,可以在很大程度上消除对流。但这忽略了一个事实,即对流也发挥着有用的作用,因为它能促进模型周围每个角落的填充。
The trick is then to preserve the useful part of the convection while minimizing or inhibiting the undesirable more violent component. Solutions do exist, but they involve processes and materials so costly as to preclude their use for mass production. A more pragmatic approach consists in finding the best compromise between the dictates of physics and manufacturing costs.
因此,诀窍在于既要保留对流的有用部分,又要尽量减少或抑制对流不可取的更剧烈的部分。解决方案确实存在,但它们所涉及的工艺和材料成本高昂,无法用于大规模生产。一种更务实的方法是在物理学原理和制造成本之间找到最佳的折衷方案。
This example is a classic illustration of the delicate balance that must be struck between fundamental advances in physics and industrial requirements. It is often not enough to propose clever solutions. We also have to contend with cost constraints. In the case of low-value-added granulars, technological advances must be quite substantial before industry will commit itself to investing in an expensive new process.
Problems are particularly varied in the light chemical synthesis and pharmaceutical industries. We will mention a few typical examples.
这个例子典型地说明了必须在物理学的基本进步和工业需求之间取得微妙的平衡。仅仅提出巧妙的解决方案往往是不够的。我们还必须面对成本限制。就低增值的颗粒物而言,在工业界承诺投资昂贵的新工艺之前,技术进步必须相当可观。
在 轻化学合成 和 制药 行业,问题尤为多样。我们将列举几个典型的例子。
Powders and various granular materials are ubiquitous in pharmacology. The specifications typical of that industry are wide-ranging. For instance, the objective may be to mix several ingredients with different and/or complementary effects in such a way that they can be readily absorbed with as pleasant a flavor as possible. Such stipulations require highly sophisticated preparation techniques.
粉末和各种颗粒材料在药剂学中无处不在。该行业的典型规格多种多样。例如,目的可能是将几种具有不同和/或互补作用的成分混合在一起,使其易于吸收并尽可能具有宜人的味道。这些要求都需要高度复杂的制备技术。
One of the best-known and simplest examples is aspirin. Its basic componentacetylsalicylic acid-is bitter to the taste and tends to cause stomach irritation.
This product, whose patent is now in the public domain, has undergone numerous improvements over the years, which are intended to minimize undesirable side effects and enhance absorption into the blood stream.
The starting crystallized powder is recompacted, coated with polysaccharides (for taste), mixed with starch (for rapid dispersion in water), and bonded to vitamin C, which gives it a yellow color on one side and white on the other (this solution gets around the difficulty of mixing the constituent powders intimately).
最著名、最简单的例子之一是阿司匹林。它的基本成分乙酰水杨酸味苦,容易引起胃部刺激。
这种产品的专利现在已经进入公共领域,多年来已经进行了许多改进,旨在最大限度地减少不良副作用,并增强其在血液中的吸收。
初始结晶粉末被再压实,用多糖(用于口味)包裹,与淀粉(用于快速分散在水中)混合,并与维生素 C 结合,使其一面呈黄色,另一面呈白色(这种解决方案避免了混合成分粉末的困难)。
Another well-known example is the production of talcum and other cosmetic products, which are typically composed of the appropriate mixtures of powders and other granulars. Here again, mixing powders by convergent flows can temporarily obstruct conduits. Such problems can play havoc with the composition of the mixtures, with potentially disastrous consequences for the safety of the product, particularly in the case of pharmaceuticals.
另一个众所周知的例子是滑石粉和其他化妆品的生产,这些产品通常由粉末和其他颗粒的适当混合物组成。在这种情况下,通过汇流混合粉末也会暂时阻塞导管。这些问题可能会破坏混合物的成分,对产品的安全性造成灾难性的后果,尤其是在药品方面。
Cosmetic and pharmaceutical powders, whether of organic or mineral origin, often go through a process of fritting, either cold or hot (such as in the fabrication of ceramics), bonding, or even extrusion. The physics of these processes is poorly understood and the thermal and mechanical properties of the starting materials are rarely known with any precision. The details are much beyond the scope of this book, but we should be aware that a number of applied physics laboratories are trying to solve these problems of great practical interest.
化妆品和药品粉末,无论是有机粉末还是矿物粉末,通常都要经过冷加工或热加工(如陶瓷制造)、粘合甚至挤压的过程。人们对这些过程的物理原理知之甚少,也很少能精确地知道初始材料的热性能和机械性能。这些细节远远超出了本书的范围,但我们应该知道,许多应用物理实验室正在努力解决这些具有重大现实意义的问题。
We will simply mention as an example the manufacture of modem magnets intended for high-performance applications, such as electric motors for high-speed trains.
They are produced by fritting powders of rare-earth compounds whose granulometry ranges from $20$ to $50\mu\text{m}$. This high-technology industry consumes several hundred tons of high-purity granular materials per year.
我们仅以高性能应用领域(如高速列车的电动机)的现代磁铁制造为例加以说明。
这些磁铁是由粒度从 $20$ 到 $50\mu\text{m}$ 不等的稀土化合物粉末熔炼而成的。这一高科技产业每年消耗数百吨高纯度颗粒材料。
Another important application of materials in powder form, or small-size granulars in general, has to do with the physical and chemical properties of their surface.
Specifically, their large surface-to-volume ratio promotes their efficient interaction with ambient gases or liquids, which gives them a distinct advantages as catalysts for chemical reactions. A straightforward calculation illustrates the potential benefits. Suppose we start with a single spherical grain of radius $R$.
粉末状材料或一般小颗粒状材料的另一个重要应用与它们表面的物理和化学特性有关。
具体来说,它们的大表面-体积比可以促进它们与周围气体或液体的有效相互作用,从而使它们在作为化学反应催化剂时具有明显的优势。一个简单的计算就能说明其潜在优势。假设我们从一个半径为 $R$ 的球形颗粒开始。
Its volume is $\frac{4}{3}\pi R^{3}$, and its surface area $S$ is $4\pi R^{2}$. If we manage to divide this single grain into $N$ spherical particles of radius $r$, we obviously have $N\approx (R/r)^{3}$. The total surface area of the $N$ small particles is now equal to $4N\pi r^{2} = 4N^{1/3}\pi R^{2} = SN^{1/3}$, which increases as the cube root of the number of particles. An increase of the surface area by a factor of $1000$ results from $27$ subdivisions, which can easily be achieved by mechanical crushing.
它的体积是 $\frac{4}{3}\pi R^{3}$,表面积 $S$ 是 $4\pi R^{2}$。如果我们设法把这颗单一的颗粒分开为 $N$ 个半径为 $r$ 的球形颗粒,显然就有 $N\approx (R/r)^{3}$。现在,$N$ 个小颗粒的总表面积等于 $4N\pi r^{2} = 4N^{1/3}\pi R^{2} = SN^{1/3}$,它随着颗粒数量的立方根而增加。细分 $27$ 次后,表面积增加了 $1000$ 倍,这可以通过机械粉碎轻松实现。
The Agriculture Industry
As is well known, many Western developed nations are major producers of agricultural and food products that often rank first on their list of exports. Despite years of steady growth, the industry has been unable to bring much improvement to its basic processing technology, particularly of granular materials such as wheat, corn, powdered milk, cocoa, and the like.
众所周知,许多西方发达国家都是农产品和食品的主要生产国,这些产品往往在其出口清单上名列前茅。尽管该行业多年来稳步增长,但其基本加工技术,尤其是小麦、玉米、奶粉、可可等颗粒材料的加工技术,一直未能得到很大改进。
A number of research centers have been created around the world in the hope of changing this state of affairs. Engineers have become increasingly aware of some of the outstanding problems concerning the processing, transport, and storage of all manner of granulars.
为了改变这种状况,世界各地成立了许多研究中心。工程师们越来越意识到有关各种颗粒的加工、运输和储存的一些悬而未决的问题。
As is the case in the chemical industry, the processing of foodstuffs falls in one of two categories, depending on the degree of value-added materials. The prototype in the low-value-added category is the animal feed industry, which uses a relatively primitive technology to handle enormous quantities of granular materials derived from agriculture. A typical plant treats hundreds of thousands of tons of various grains per year.
与化学工业一样,食品加工根据材料的增值程度分为两类。低增值类别的原型是动物饲料行业,该行业使用相对原始的技术处理来自农业的大量颗粒材料。一个经典的工厂每年处理数十万吨各种谷物。
A small portion of its budget-usually around 9%-is earmarked for processing, while 83% covers the raw materials (mostly of agricultural origin), and 8% is devoted to transport.
It is not uncommon to notice in such facilities hoppers pockmarked with numerous dents left by hammer blows intended to free flow blockages caused by arch effects. Materials such as flour are prone to creating solid plugs.
It is a fact of life that these blockages have to be routinely cleared with pick axes, if not jackhammers.
其预算的一小部分–通常约为 $9$%–专门用于加工,$83$%用于原材料(主要是农产品),$8$%用于运输。
在这些设施中,经常可以看到料斗上有许多锤子击打留下的凹痕,这些锤子击打的目的是为了消除拱形效应造成的流动阻塞。面粉等物料很容易形成固体堵塞物。
事实是,这些堵塞物即使不用手工锤,也必须经常用镐清理。
A quick survey of the problems affecting daily operations in such plants reveals that they are almost exclusively of two types-blockages of flow by the arch effect, and granular separation.
对影响这类工厂日常运行的问题进行简单调查后发现,这些问题几乎都是两类–桥型效应造成的流动阻塞和颗粒分离。
1.2.2 Flow Problems
Granular flows have properties that give rise to numerous problems in industrial settings. Much can be learned by observing the flow of grains in an ordinary hourglass filled with sand. Contrary to what happens in sealed-off hourglasses of the type once used to keep track of time, the flow of sand in cone-shaped funnels is generally not smooth.
颗粒流动的特性会给工业环境带来许多问题。通过观察装满沙子的普通沙漏中的颗粒流动,我们可以学到很多东西。与曾经用来记录时间的密封沙漏中的情况相反,锥形漏斗中的沙粒流动通常并不平滑。
We know from experience that the coupling between the granular flow and the ambient fluid can cause intermittent events that impart to the exiting flux of material a discontinuous character.
How granular materials flow down industrial-size hoppers turns out to be a rather tricky problem that has been the subject of a great many studies. Yet the physics of this seemingly simple phenomenon remains poorly understood.
我们从经验中了解到,颗粒流和环境流体之间的耦合会导致间歇性事件,从而使流出的物料流具有不连续的特点。
颗粒物料如何从工业规模的料斗中流下是一个相当棘手的问题,已经成为许多研究的主题。然而,人们对这一看似简单的物理现象仍然知之甚少。
Virtually all industrial or laboratory facilities designed to handle granular materials such as grains (food industry) or gravels (construction industry and public works) are plagued by blocked flows which can be extremely disruptive. Blockages of this type occur with annoying regularity, for instance, while trucks or barges are being loaded with gravel through giant chutes designed to handle tens of tons of material, as schematically illustrated in Figure 4.
几乎所有用于处理谷物(食品工业)或砾石(建筑业和公共工程)等颗粒状材料的工业或实验室设施都会受到堵塞流的困扰,这可能会造成极大的破坏。例如,当卡车或驳船通过可处理数十吨物料的巨型槽装载砾石时,就会经常出现此类堵塞,如图 4 所示。
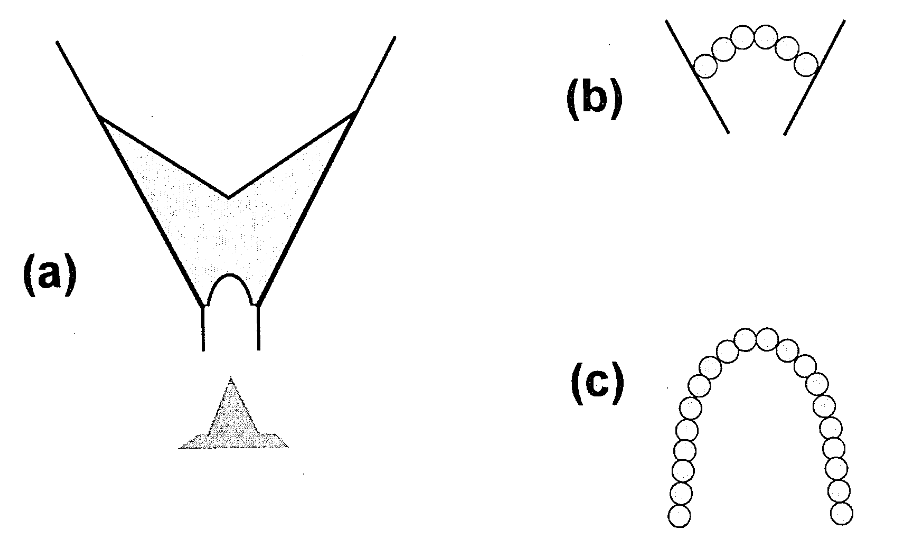
Diagrams (a) and (b) show flow blockages due to the formation of arches near the orifice of an hourglass or a hopper. Diagram (c) depicts an arch structure with maximum stability (inverted chain).
图(a)和(b)显示的是由于在沙漏或料斗的孔口附近形成拱形而导致的流动阻塞。图 (c) 显示了具有最大稳定性的拱形结构(倒链)。
The frequency of these events depends on the diameter of the opening, as well as on the size and mechanical properties of the aggregates. They can invariably be traced to the formation of arches in the vicinity of the discharge orifice. Depending on the circumstances, the flow can either become sporadic or be completely blocked by remarkably stable arches.
这种情况发生的频率取决于排料口的直径以及聚集体的大小和机械特性。这些现象总是与排料口附近形成的拱形结构有关。根据具体情况,流动既可能是间歇的,也可能被非常稳定的"桥"完全阻断。
For the same reason, it is extremely difficult to reproducibly mix two granular materials by merging two separate flows into a common discharge channel. That has proven to be a major problem in the food industry and in chemical plants producing polymers, where raw materials are typically dry granulars. Blockages can form spontaneously as a result of some kind of seizing mechanism. The phenomenon is even known to have caused dangerous explosions by allowing fermentation gases to accumulate in grain silos plugged up by such arches.
出于同样的原因,通过将两股独立的颗粒流汇入一个共同的排放通道来重复混合两种颗粒状物料是极其困难的。事实证明,这在食品工业和生产聚合物的化工厂是个大问题,因为这些工厂的原料通常是干燥的颗粒状物料。堵塞可能由于某种卡死机制而自发形成。据了解,这种现象甚至会导致发酵气体积聚在被这种桥型堵塞的粮仓中,从而引发危险的爆炸。
Given the many uncertainties surrounding the static properties of a granular system, it would seem that describing the mechanism of arch formation would be quite a daunting problem. Nevertheless, it is possible to state a number of general principles which will later prove useful.
It is important to realize that arches, which are a direct consequence of gravitational forces, can form because of purely geometrical and steric reasons. This can be easily understood by considering a stack of identical frictionless spheres resting on either side against inclined walls, as depicted in Figure 4(b).
鉴于颗粒系统的静态特性存在许多不确定因素,描述桥型形成的机理似乎是一个相当艰巨的问题。尽管如此,我们还是可以提出一些基本原则,这些原则将在日后被证明是有用的。
重要的是要认识到,拱桥是重力的直接结果,也可能由于纯粹的几何和立体原因而形成。如图 4(b)所示,将一叠完全相同的无摩擦球体放在倾斜墙壁的两侧,就可以很容易地理解这一点。
In this example, each sphere is kept in equilibrium at two contact points whose connecting line lies below the center of gravity. While such arrangements can obviously form spontaneously in two-dimensional systems, they would seem rather more improbable in real-life three-dimensional situations, because they require the cooperation of a much larger number of spheres, each stabilizing its neighbors.
Nevertheless, they are frequently encountered in industrial or laboratory conditions. Figure 5 illustrates some examples actually observed in simple experiments.
在这个例子中,每个球体都在两个连线位于重心下方的接触点上保持平衡。这种排列方式显然可以在二维系统中自发形成,但在现实生活中的三维环境中似乎更不可能,因为它们需要更多球体的合作,每个球体都要稳定其相邻的球体。
不过,在工业或实验室条件下,它们还是会经常出现。图 5 展示了一些在简单实验中实际观察到的例子。

Stable arches form readily when a $1\text{ cm}$ diameter test tube filled with fine sand ($100 \mu\text{m}$) is turned upside down. The photo on the left provides a side view, while the one on the right is taken from below to reveal the arch pinned against the wall.
将直径为 $1\text{ cm}$、装满细沙($100\mu\text{m}$)的试管倒置,很容易形成稳定的拱型。左边的照片是侧视图,右边的照片是从下面拍摄的,可以看到拱门被固定在壁上。
Not surprisingly, the phenomenon of dry friction greatly increases the likelihood of forming arches anchored onto the side walls. In this case, it is not even necessary for the side walls to be slanted.
Indeed, we will run into several examples of arches pinned against vertical walls (e.g., Section 3.2.4), particularly in silos. Effects of this type can have dangerous consequences in industrial facilities. Engineers have come up with a number of more or less effective solutions, such as those illustrated in Figure 6.
毫不奇怪,干燥摩擦现象大大增加了在侧壁上形成锚固拱形的可能性。在这种情况下,侧墙甚至无需倾斜。
事实上,我们会遇到一些拱型被固定在垂直墙壁上的例子(如第 3.2.4 节),尤其是在筒仓中。这种影响会给工业设施带来危险后果。工程师们提出了许多或多或少有效的解决方案,如图 6 所示。
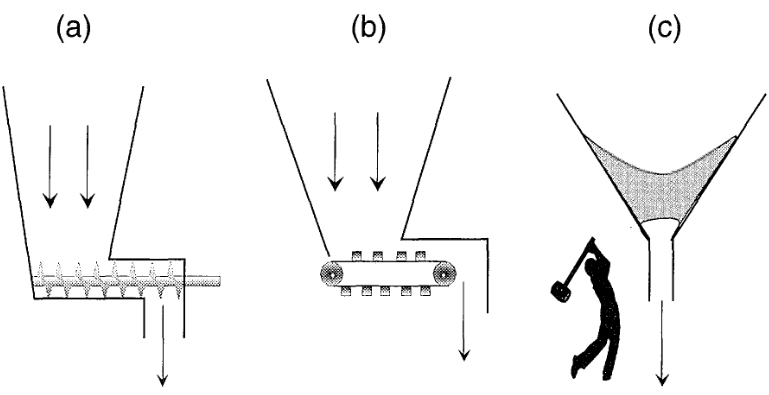
Three methods used in industry to prevent or remedy blockages by arch effect. They include (a) an Archimedes screw, and (b) a conveyor belt with a corrugated surface. In (c), a plant worker pounds an obstructed hopper with a sledge hammer to get the flow started again. The latter is the method of choice in industries producing low-value-added granular materials.
工业中防止或补救拱形效应所致堵塞的三种方法。它们包括:(a) 阿基米德螺旋;(b) 表面有波纹的传送带。在(c)中,工厂工人用大锤敲击受阻的料斗,使其重新开始流动。后者是生产低增值颗粒材料的行业的首选方法。
1.2.3 Problems of Segregation
The industry processes enormous quantities of granular materials year in and year out. Virtually every stage of its operations is at the mercy of segregation-a most irksome phenomenon that tends to separate the components of a mixture supposed to be as homogeneous as possible.
It is a perennial problem, for instance, in the polymer industry, which often relies on solid phase reactions between dry granulars that must first be mixed or fused as evenly as possible.
该行业年复一年地加工大量的颗粒材料。几乎每一个操作环节都会受到离析现象的影响–这种最令人讨厌的现象往往会将本应尽可能均匀的混合物的成分分离开来。
这是一个长期存在的问题,例如,在聚合物行业,通常需要在干燥颗粒之间进行固相反应,而这些颗粒必须首先尽可能均匀地混合或融合。
It is no less of a challenge in the agriculture industry, which tries to produce carefully controlled mixtures of various grains and other proteins in granular fornl. Industries that deal with low-value-added materials, such as animal feed, cannot afford sophisticated technologies that would add excessive cost to their products. They rely mostly on relative crude and not very effective techniques, of the type illustrated in Figure 7.
对于农业来说,这也是一个挑战,因为农业需要生产各种谷物和其他蛋白质的颗粒状混合物。经营低增值材料(如动物饲料)的行业无法负担会增加产品过多成本的尖端技术。他们主要依靠图 7 所示的相对粗糙和不太有效的技术。
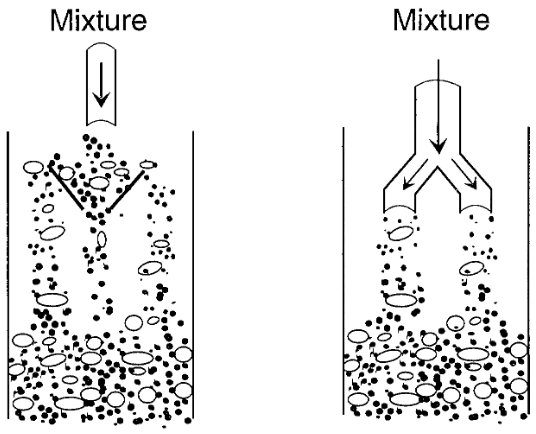
Two techniques used in industry to try to avoid problems of granular segregation. The principle is the same in both cases. The idea is to force the materials through a section of hardware that promotes mixing.
工业中用来避免颗粒分离问题的两种技术。两者的原理相同。其原理是强制材料通过一段能促进混合的硬件。
At the other end of the spectrum, the example we are about to discuss illustrates the difficulties faced by industries such as plastics or pharmaceuticals. It will give us an idea of the costly investments required when it is absolutely essential to achieve intimate mixing of different granular materials.
The problem boils down to this: Two granular materials A and B must be mixed in equal ratios and as uniformly as possible. The criterion for homogeneity is that every particle of A be in contact with at least one particle of B in order to ensure the proper reaction or fusion between the two components.
在另一端,我们将要讨论的例子说明了塑料或制药等行业所面临的困难。通过这个例子,我们可以了解到,当必须实现不同颗粒材料的紧密混合时,所需的投资是多么昂贵。
问题可归结为以下几点:两种颗粒状材料 A 和 B 必须以相等的比例尽可能均匀地混合。均匀性的标准是每一粒 A 颗粒至少与一粒 B 颗粒接触,以确保两种成分之间发生适当的反应或融合。
Simply dumping equal quantities of the two products in an ordinary mixer will not do since, as we have pointed out, shaking the resulting mixture inescapably tends to separate the two components.
The technique currently favored both in industry and laboratories turns out to be costly, labor-intensive, slow, and-least attractive of all-difficult to adapt to mass production.
简单地将等量的两种产品倒入普通的混合器中是不行的,因为正如我们所指出的,摇动混合物会不可避免地使两种成分分离。
目前在工业界和实验室中普遍采用的技术成本高、劳动密集、速度慢,而且最不吸引人的是难以适应大规模生产。
But it is perfectly adequate to manufacture modest quantities of materials. Rather than trying to prepare a homogeneous mixture-which is virtually impossible to achieve-the solution is to make a sort-layered cake, with alternating sheets of A and B.
The trick is to start with what amounts to two separate sheets of pie dough, one loaded with particles of the material A, and the other with particles of B. These two sheets are laid on top of each other, as depicted in Figure 8(a).
但它完全足以制造适量的材料。与其试图制备均匀的混合物(这几乎是不可能实现的),不如制备一种"分层蛋糕",A 和 B 交替排列。
诀窍就在于,先将两层分开,一层中装有 A 材料的颗粒,另一层中装有 B 材料的颗粒。如图 8(a) 所示,这两层叠放在一起。
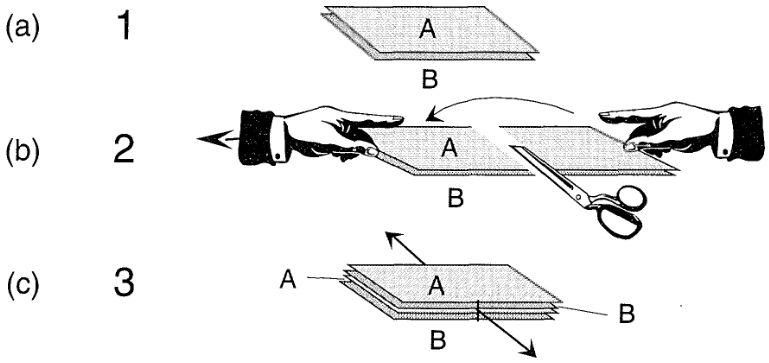
Illustration of the “pastry-maker” technique to mix two different granular materials (after [115]).
混合两种不同颗粒材料的 “糕点师” 技术图解
The sequence of steps illustrated in the rest of Figure 8 is referred to as “the pastry-maker technique.” The initial $A/B$ matrix is stretched in one direction so as to double its length. It is then cut in two (Figure 8(b)), and the two separate pieces are placed on top of each other (Figure 8(c)), resulting in an $A/B/A/B$ structure.
图 8 其余部分所示的一系列步骤被称为 “糕点师技艺”。将初始的 $A/B$ 方阵向一个方向拉伸,使其长度增加一倍。然后将其一分为二(图 8(b)),并将两块独立的方阵叠放在一起(图 8(c)),形成一个 $A/B/A/B$ 结构。
The process is repeated until the thickness of each individual layer is roughly equal to that of the largest of the two particles $A$ or $B$. At the conclusion of $N$ operations, the number of layers is obviously $2^{N}$ . Not only is the process extremely labor-intensive, but the final product is only a superposition of different layers, rather than a true three-dimensional mixture.
这个过程不断重复,直到每一层的厚度大致等于两个粒子 $A$ 或 $B$ 更大的那个尺度。在完成 $N$ 次操作后,层数显然为 $2^{N}$。这个过程不仅耗费大量人力,而且最终产品只是不同层的叠加,而不是真正的三维混合物。
The process just described has been adapted to mass-production with so-called Kenics mixers, illustrated in Figure 9, which accomplish, automatically and continuously, the discrete sequence of steps of the pastry-maker technique.
The pastes or fluids to be mixed are injected at points A and B shown in the figure. The ultimate speed of the process is limited by the onset of turbulence phenomena which may appear within the reactor and can potentially upset the quality and smoothness of the mixing.
Such phenomena depend primarily on the dimensions of the apparatus and the properties of the products to be mixed.
图 9 所示的 Kenics 搅拌机可自动、连续地完成 “糕点制作工艺” 的一系列离散步骤。
要混合的浆料或流体分别注入图中所示的 A 点和 B 点。该工艺的最终速度受到湍流现象的限制,湍流现象可能出现在反应器内,并有可能破坏混合的质量和平稳性。
这种现象主要取决于设备的尺寸和待混合产品的特性。
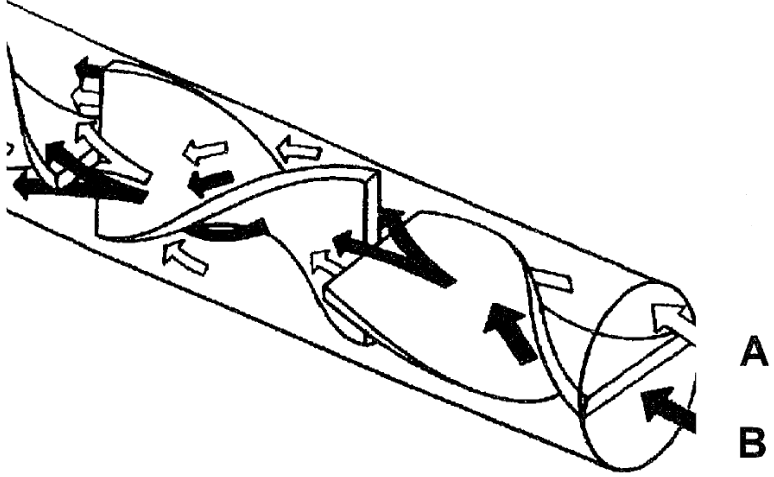
The first two elements of a Kenics mixer
Kenics 混合器的前两个要素
It is clear that implementing this technology on the factory floor requires a large capital investment and has to contend with difficult processing techniques (the preparation of pastes can itself be a challenge).
As such, it is largely incompatible with the processing of industrial quantities of low-value-added materials, whose cost has to be kept as low as possible. A better understanding of the mechanism of segregation in granular materials is of great importance not only from a fundamental physics point of view but for economic reasons as well.
显然,在工厂车间实施这项技术需要大量的资金投入,而且还必须与困难的加工技术作斗争(浆料的制备本身就是一项挑战)。
因此,它在很大程度上与低增值材料的工业加工不相容,而低增值材料的加工成本必须尽可能低。更好地了解颗粒材料的离析机理不仅从基础物理学的角度来看非常重要,从经济学的角度来看也是如此。
1.3 Granular Materials and Geophysics
To state that granular materials are ubiquitous in nature is practically a cliche. Sand is present in enormous quantities in deserts, which happen to cover more than $10$% of the land surface of the globe.
The shore line of oceans and lakes, as well as ancient sea bottoms, constitute virtually inexhaustible natural sources of silicate sands, one of the basic materials in our civilization.
说颗粒状物质在自然界无处不在几乎是老生常谈。沙子大量存在于沙漠中,而沙漠的面积 恰好 占全球陆地面积的 $10$% 以上。
海洋和湖泊的岸线以及古老的海底几乎构成了硅酸盐沙取之不尽的天然资源,而硅酸盐沙正是我们人类文明的基本材料之一。
Numerous natural phenomena depend to varying degrees on the type of physics we are about to describe. If nothing else, most involve some basic mechanisms, such as collisions and friction, that govern the behavior of dry granular media. By and large, geophysics concerns itself with much more complex objects than those of interest to us here. For instance, the physics of moving sand-made of particles in suspension in a liquid-falls in the realm of fluidized beds, which is rather different from the types of problems addressed in this book.
许多自然现象在不同程度上取决于我们将要描述的物理学类型。如果不出意外,大多数现象都涉及一些基本的机制,如碰撞和摩擦,它们支配着干燥颗粒介质的行为。总的来说,地球物理学关注的对象要比我们在此感兴趣的对象复杂得多。例如,由悬浮在液体中的颗粒组成的移动沙子的物理学属于流化床的范畴,这与本书所讨论的问题类型大相径庭。
On the other hand, an avalanche of snow in a state of supersaturation may be understood in terms of concepts that will be discussed in Chapter 4 (although not all the experts agree on this point).
A great deal of caution is warranted in these areas, even though models are largely heuristic and, as such, ought to be applicable in principle to a variety of avalanche phenomena, regardless of their specific nature.
另一方面,处于过饱和状态的雪崩可以用第 4 章将讨论的概念来理解(尽管并非所有专家都同意这一点)。
尽管模型在很大程度上是启发式的,因此原则上应该适用于各种雪崩现象,而不论其具体性质如何,但在这些领域仍需慎之又慎。
In the same spirit, there exists a certain analogy between the phenomenon of granular separation by shearing, to be addressed in Chapter 5, and that of stratified sedimentation in rivers churning rocks or sand. This type of stratification occurs in nature on massive scales, covering the entire length of a river or the height of a mountain.
本着同样的精神,第 5 章将讨论的颗粒剪切离析现象与河流搅动岩石或沙子造成的分层沉积现象之间存在某种相似性。在自然界中,这种分层现象规模巨大,可覆盖整条河流的长度或一座山的高度。
This explains at least in part how rivers shift course over periods of centuries, how they become clogged with sand, and other natural phenomena with great ecological consequences.
Likewise, the friction experienced by rocks subject to high winds or falling down steep slopes contributes directly to the erosion of our planet’s surface and has a profound effect on the evolution of our environment.
It would obviously be much to our advantage to be able to predict the overall behavior of all these natural phenomena.
这至少在一定程度上解释了河流如何在几个世纪的时间里改变流向,如何被沙子堵塞,以及其他对生态产生重大影响的自然现象。
同样,受到大风吹袭或从陡坡上掉落的岩石所经历的摩擦力直接造成了地球表面的侵蚀,并对我们环境的演变产生了深远的影响。
如果能够预测所有这些自然现象的整体行为,显然对我们大有裨益。
To a modest extent, the principles discussed in this book may well bring us one step closer to this ambitious goal. Indeed, the material covered in subsequent chapters can be viewed as a description from first principles of various mechanisms at play in our geophysical environment.
在一定程度上,本书所讨论的原理很可能会让我们离这一宏伟目标更近一步。事实上,后续章节所涉及的材料可以看作是对地球物理环境中各种作用机制的第一原理描述。
Another discipline that, in many respects, has much in common with the physics of dry granular materials is seismology. How forces of friction are stored and suddenly released is just as much of interest to geophysicists as it is to fundamental theorists trying to understand the basic properties of granulars.
地震学是另一门(在许多方面)与干燥颗粒材料物理学有许多共同之处的学科。地球物理学家和试图了解颗粒基本特性的基础理论家一样,都对摩擦力如何储存和突然释放感兴趣。
The collective behavior of particles in quasi-permanent contact is the central focus of the geophysical sciences. Granted, geophysicists typically deal with interactions that are far more complex than those to which we will deliberately restrict our attention.
准永久接触粒子的集体行为是地球物理科学的核心焦点。当然,地球物理学家通常要处理的相互作用远比我们刻意关注的要复杂得多。
They have to worry about phenomena such as cohesion effects, contact fatigue, erosion, strain hardening, and many others that we shall barely touch upon.
Yet, the phenomenon of fracturing, which is at the basis of geophysics, shows up just as faithfully, albeit in an elementary form, in the most grossly simplified versions of the physics of granulars, as we will see in Chapter 3.
他们不得不担心诸如内聚效应、接触疲劳、侵蚀、应变硬化等现象,还有许多其他现象,我们几乎不可能触及。
然而,正如我们将在第 3 章中看到的那样,作为地球物理学基础的断裂现象,尽管只是以最基本的形式出现,但在最粗略简化的颗粒物理学版本中也同样真实地存在。
Avalanches and free flows are treated in Chapter 4, in which we draw liberally from the work of geophysicists. We do so for at least two reasons. First, an accurate description of what is called the stick-slip phenomenon requires a clear understanding of the interdependence between friction and velocity, which also happens to be at the heart of the physics of granular materials.
第 4 章讨论了雪崩和自由流动,其中我们大量借鉴了地球物理学家的研究成果。我们这样做至少有两个原因。首先,要准确描述所谓的 粘滑 现象,就必须清楚地了解摩擦力与速度之间的相互依存关系,而这恰好也是颗粒材料物理学的核心。
Second, the simulation of so-called self-organized critical (SOC) systems has been called upon to explain both granular avalanches and the scaling laws of the distribution of earthquakes (typified by the Gutenberg-Richter law). The validity of this approach remains a topic of lively debate in both cases.
其次,模拟所谓的 “自组织临界(SOC)系统” 被用来解释颗粒雪崩和地震分布的尺度规律(以 Gutenberg-Richter 定律为典型)。在这两种情况下,这种方法的有效性仍然是一个争论不休的话题。
一个地震学定律.
$$ \log_{10}{N} = a - bM $$
其中 $N$ 表示震级大于 $M$ 的地震数,$a$ 和 $b$ 是常数,$M$ 是地震的震级。该定律表明,地震的震级越大,发生的频率越小。
1.4 A Brief Historical Review
In the past, the physics of granular materials has received far less attention on the part of researchers than, say, hydrodynamics.
Yet, it is remarkable and, in a sense, admirable that a few notable scientists managed in those days to marvel at some fascinating aspects of the behavior of these types of solids.
过去,颗粒材料物理学受到的研究者的关注远远不及流体力学。
然而,值得注意的是,在那个时代,一些杰出的科学家(超越自己的时代)意识到这些固体的行为的一些迷人的方面,这在某种意义上是令人钦佩的。
The first recorded mention of granular flows is due to Lucretius (ca. 98-55 B.C.), the famous poet and natural philosopher in ancient Rome. He wrote in 55 B.C.: “One can scoop up poppy seeds with a ladle as easily as if they were water and, when dipping the ladle, the seeds flow in a continuous stream.”
首次记录提及颗粒流动的是卢克莱修斯(Lucretius)(公元前 98-55 年),他是古罗马著名的诗人和自然哲学家。他在公元前 55 年写道:“人们可以用勺子舀起罂粟籽,就像舀水一样容易,当用勺子舀起时,种子会流成一条连续的流。”
The scholars of the Renaissance had wide-ranging interests. Leonardo da Vinci (1452-1519) was the first to devise a simple and convincing experiment demonstrating the laws of dry friction.
He and others were even able to make a few pertinent statements concerning piles of sand. It was not until the end of the eighteenth century, though, that Charles de Coulomb (1736-1806) wrote a definitive paper, which is still frequently cited, entitled “Essay on the rules of Maximis and Minimis applied to some problems of equilibrium related to architecture”.
文艺复兴时期的学者们兴趣广泛。达芬奇(Leonardo da Vinci)(1452-1519 年)是第一个设计出简单而令人信服的实验来证明干燥摩擦定律的人。
他和其他人甚至还能对沙堆做出一些相关的说明。不过,直到十八世纪末,查尔斯-德-库仑(Charles de Coulomb)(1736-1806 年)才撰写了一篇题为 “关于最大和最小规则应用于与建筑有关的一些平衡问题的论文” 的权威论文,该论文至今仍经常被引用。
The paper in question, which is of interest in several respects, is based on a number of experimental observations on the equilibrium of earthen embankments, the stability of stone structures, and other edifices. It puts the physics of granular materials on a foundation that is difficult to contest even today.
For instance, it ultimately led to the celebrated Coulomb laws of dry friction between solids, which in time would be extended to granular materials. In that sense, Coulomb’s seminal paper can be viewed as heralding an entirely new discipline.
这篇论文基于对土堤平衡、石结构稳定性和其他建筑的大量实验观察,在多个方面都很有意义。它将颗粒材料的物理学建立在一个即使在今天也难以质疑的基础之上。
例如,它最终导致了著名的固体间干燥摩擦的库仑定律,并在一定时间内扩展到颗粒材料。从这个意义上说,库仑的这篇开创性论文可以被视为一门全新学科的先驱。
In 1780, Ernst Chladni (1756-1827) noticed a number of interesting differences (which remain rather puzzling even today) between the behavior of light granulars (such as horse hair) and that of coarser and heavier ones (such as sand). He observed what came to be known as Chladni’s complementary figures, which we will discuss in Chapter 2.
His experiments were duplicated and confirmed a short while later by Christiaan Oerstedt (1777-1851), who used lycopodium powder-an extremely fine material that was instrumental in many other discoveries. Felix Savart (1791-1841) was interested, among other things, in music. He would make use in 1827 of Chladni’s geometric figures to study the frequencies and wavelengths of sound waves.
1780 年,恩斯特-克拉德尼(Ernst Chladni,1756-1827 年)注意到轻质颗粒(如马鬃)与较粗、较重的颗粒(如沙子)在行为上存在一些有趣的差异(这些差异至今仍令人费解)。他观察到了后来被称为 Chladni 互补图形的现象,我们将在第 2 章对此进行讨论。
不久之后,克里斯蒂安-奥斯特(Christiaan Oerstedt,1777-1851 年)复制并证实了他的实验。费利克斯-萨瓦特(Felix Savart,1791-1841 年)主要对音乐感兴趣。1827 年,他利用克拉德尼的几何图形研究声波的频率和波长。
Michael Faraday (1791-1867) was another illustrious figure who, against the backdrop of his primary work on hydrodynamic instabilities, also had a strong interest in how vibrations induce the formation of sand piles. This phenomenon, closely related to Chladni’s experiments, remained a mystery until recently. The problem was to figure out the role of air as sand collects in regular patterns. Chapter 3 will provide an opportunity to discuss the problem of granular instabilities, reminiscent of those observed in liquids by Faraday, as well as the formation of sand piles.
迈克尔-法拉第(Michael Faraday,1791-1867 年)是另一位杰出人物,他的主要研究领域是流体力学不稳定性,同时他还对振动如何诱发沙堆的形成有着浓厚的兴趣。这一现象与克拉德尼的实验密切相关,直到最近仍是一个谜。问题是要弄清空气在沙子有规律地聚集时所起的作用。第 3 章将讨论颗粒不稳定性问题,让人想起法拉第在液体中观察到的不稳定性,以及沙堆的形成。
William Rankine (1820-1872) examined the theoretical implications of friction in granular materials as early as 1857. Starting from Coulomb’s ideas, he established a number of principles which remain fully valid to this day. He defined what is now called Rankine’s passive and active states. These concepts are clearly and thoroughly discussed in the book by Brown and Richards, and we will not dwell on them here.
威廉-兰金(William Rankine,1820-1872 年)早在 1857 年就研究了颗粒材料摩擦的理论意义。他从 Coulomb 的观点出发,建立了一系列至今仍然完全有效的原则。他定义了现在所谓的 Rankine 被动状态和主动状态。布朗和理查兹在书中对这些概念进行了清晰而详尽的论述,我们在此不再赘述。
The problem of the equilibrium distribution of forces in a granular medium stored in a silo has been studied by several researchers, who have published the results of their work. In 1884, I. Roberts noted that “in a structure whose lateral walls are parallel, the pressure exerted by the stored grain onto the base ceases to increase when the structure is filled to a height more than twice the diameter of the inscribed circle”. A few years later, H. Janssen, a German engineer from the city of Bremen, proposed a model based on a coefficient describing the redirection offorces toward the wall.
多位研究人员对筒仓中储存的颗粒介质的平衡态分布问题进行了研究,并发表了研究成果。1884 年,I. Roberts 指出,"在侧壁平行的结构中,当结构被填充到超过内切圆直径两倍的高度时,储存谷物对底座施加的压力就不再增加"。几年后,Bremen 的德国工程师 H. Janssen 提出了一个模型,该模型基于一个描述力向墙壁重新定向的系数。
He failed to refer to the work of Roberts, presumably because he was unaware of it. We will present the model in Chapter 3, and even generalize it to the dynamics of granular systems. Substantially the same idea inspired the work of John Strutt (1842-1919), published in 1906. He mentioned Roberts’ observation but not Janssen’s work-again because he probably was not familiar with it. Incidentally, Strutt (who is perhaps better known as Lord Rayleigh, winner of the 1904 Nobel Prize in physics) suggested an interesting analogy between this problem and the way a rope wrapped around a pole resits traction.
他没有提到 Roberts 的研究成果,大概是因为他对其并不了解。我们将在第 3 章介绍这一模型,甚至将其推广到颗粒系统的动力学中。约翰-斯特拉特(John Strutt,1842-1919 年)于 1906 年发表的著作也基本上受到了同样思想的启发。他提到了 Roberts 的观察结果,但没有提到杨森的工作–这也是因为他可能并不熟悉 Janssen 的工作。顺便提一下,Strutt(他更为人所知的名字可能是 Lord Rayleigh ,1904 年诺贝尔物理学奖得主)提出了一个有趣的类比,把这个问题与缠在杆子上的绳子承受牵引力的方式相提并论。
By the latter part of the nineteenth century, Osborne Reynolds (1842-1912) had already distinguished himself in the field of hydrodynamics (Reynolds’s number). He also made some fundamental contributions to the theory of granulars around the year 1885. Some concepts he developed (notably that of dilatancy, which we will discuss in Chapter 3) and his analysis of slanted embankments remain high on the list of modern topics of investigation.
十九世纪后半叶,Osborne Reynolds(1842-1912 年)已在流体力学(Reynolds 数)领域卓有建树。1885 年前后,他还对颗粒理论做出了一些基本贡献。他提出的一些概念(特别是我们将在第 3 章中讨论的膨胀性概念)和他对斜堤的分析仍然是现代研究课题中的重要内容。
The number of scientists and engineers who have devoted their talents to this discipline has grown steadily during the twentieth century, particularly since the 1950s. One individual deserves to be singled out. His name is Ralph A. Bagnold. Between 1940 and 1970, he made many important observations and wrote a book on desert sands that has become a classic. Since that time, the number of scientific publications in that field has mushroomed. Indeed, this proliferation was one of the main incentives for writing this book, as we have indicated in the Preface.
在二十世纪,特别是自二十世纪五十年代以来,为这一学科奉献才智的科学家和工程师的人数稳步增长。其中有一个人值得一提。他的名字叫拉尔夫-A-巴格诺德(Ralph A. Bagnold)。在 1940 年至 1970 年期间,他进行了许多重要的观测,并撰写了一本关于沙漠中沙土的书,其已成为经典之作。从那时起,该领域的科学出版物数量如雨后春笋般增长。事实上,正如我们在序言中所指出的,这种激增是我们撰写本书的主要动力之一。
1.5 Prerequisites and Selected Bibliography
Before tackling the remainder of this book, the reader is encouraged to familiarize himself (or herself) with a few basic or review articles, which provide a bird’s eye view of the problems related to the “physics of sand piles.” Among others, we strongly recommend references. For the physics and mechanics of granular materials, the text by Brown and Richards is widely considered the ultimate reference, and rightly so, even though it is unfortunately out of print.
在学习本书的其余部分之前,我们建议读者先熟悉一些基础文章或综述文章,这些文章提供了与 “沙堆物理” 相关问题的鸟瞰图。其中,我们强烈推荐参考文献。就颗粒材料的物理和力学而言,Brown 和 Richards 的著作被广泛认为是终极参考书,尽管该书已不幸绝版,但这是正确的。
The texts by Bagnold and Nedderman are also recommended. Some more recent works, published in the format of proceedings of various specialized symposia, are also useful sources. They offer in-depth analyses of some of the issues outlined in this book.
Bagnold 和 Nedderman 的著作也值得推荐。一些以各种专业研讨会论文集形式出版的最新著作也是有用的资料来源。它们对本书概述的一些问题进行了深入分析。
As stated in the Preface, the goal of this text is to present concepts and results that are as recent as possible. In that spirit, we assume that the reader is familiar with fundamental concepts (such as the Mohr-Coulomb model, the Rankine states, the method of characteristics, and so forth). They are treated in detail in the book by Brown and Richards or in the text by Savage. The kinetic theories developed in the 1980s would by themselves justify an entire book the size of this one. They concern themselves with relatively dilute particulates in rapid motion. This is quite different from concentrated granular media, the topic which the present text is entirely devoted to. Readers interested specifically in kinetic theories are referred to other basic sources.
如前言所述,本文的目标是尽可能介绍最新的概念和结果。本着这一精神,我们假定读者已熟悉基本概念(如 Mohr-Coulomb 模型、Rankine 态、特性法等)。Brown 和 Richards 的书或 Savage 的文章中都有详细论述。20 世纪 80 年代发展起来的动力学理论本身就足以写成像本书这么大的一整本书。这些理论关注的是快速运动中的相对稀释颗粒。这与浓缩的颗粒介质截然不同,而本教材的主题正是浓缩的颗粒介质。对动力学理论感兴趣的读者可以参考其他基本资料。
2 Interactions in Granular Media
2.1 A Single Particle and Its Environment
The physics of granular materials concerns itself with real-life situations in which solid particles typically find themselves in a gas environment (usually air) or in a liquid. The properties of granulars depend primarily on the nature of the interactions between the particles themselves, but also between the particles and their environment. When the influence of the environment can be neglected, we deal with what is called dry granular materials.
Otherwise, the resulting systems can be quite complex and exhibit a variety of behaviors depending on the media involved. This field of study, which has considerable industrial applications, encompasses a broad range of media, from pastes to liquid muds to porous materials. It has been the object of a large number of studies.
颗粒材料物理学关注的是固体颗粒通常处于气体环境(通常是空气)或液体环境中的真实情况。颗粒材料的特性主要取决于颗粒本身之间的相互作用性质,同时也取决于颗粒与其环境之间的相互作用性质。当环境的影响可以忽略不计时,我们处理的就是所谓的干燥颗粒材料。
不然,所产生的系统可能相当复杂,并根据所涉及的介质表现出各种行为。这一研究领域在工业上应用广泛,涵盖了从糊状物、液态泥浆到多孔材料等多种介质。它已成为大量研究的对象。
While this topic is in the midst of rapid development, it remains largely outside the scope of this book, which focuses deliberately on a highly simplified approach in which interactions are reduced to a minimum, as opposed to the much more complicated interactions characteristic of “moist” granular materials. In what follows, we shall concern ourselves almost exclusively with dry granulars.
These have not always commanded much in the way of sustained interest on the part of the physics research community, in spite of the many different possible behaviors and fundamental nature of the problems involved, which would normally be expected to pique the curiosity of physicists and industrial engineers.
与 “潮湿” 颗粒材料所特有的复杂得多的相互作用相比,本书特意将重点放在高度简化的方法上,将相互作用降到最低程度。在下文中,我们将几乎只讨论干燥颗粒材料。
尽管所涉及的问题有许多不同的可能行为和基本性质,通常会激发物理学家和工业工程师的好奇心,但物理研究界对这些问题的持续兴趣并不浓厚。
It should be borne in mind that dry granular materials, in which interactions are simplified and reduced to friction and collisions between particles or with the container walls, are something of a “theoretical” species, as it were. It would seem that such idealized objects might be fairly accurately approximated in the laboratory by placing solid particles in a vacuum chamber. In practice though, things are rarely that simple because of a major intrinsic problem.
As it turns out, the energy dissipated through mutual collisions or friction is inevitably accompanied by the appearance of surface electrical charges on both the particles themselves and the walls of the container.
应该牢记的是,干燥颗粒材料中的相互作用被简化为颗粒之间或颗粒与容器壁之间的摩擦和碰撞,可以说是一种 “理论” 类型。在实验室中,将固体颗粒置于真空室中,似乎可以相当精确地近似这种理想化的物体。但实际上,由于一个重大的内在问题,事情很少那么简单。
事实证明,通过相互碰撞或摩擦耗散的能量不可避免地会在粒子本身和容器壁上产生表面电荷。
Such surface charges are particularly difficult to eliminate in vacuum; the resulting medium-range electrostatic interactions can greatly complicate the analysis of experimental results. Adding a surrounding fluid makes it much easier to drain away those pesky surface charges. For that reason, such a fluid is not only desirable, but indeed essential.
Fortunately, provided a few precautions are observed, a fluid matrix does not necessarily preclude treating many laboratory, or even industrial, situations involving granulars as though the materials were truly dry. The purpose of this section is to define the range of validity of the methodologies which we will develop throughout this book. For strictly pedagogical reasons, we start out by discussing the interactions of a single particle with its fluid environment.
这种表面电荷在真空中尤其难以消除;由此产生的中程静电相互作用会使实验结果的分析变得非常复杂。添加一种周围流体可以更容易地去除这些讨厌的表面电荷。因此,这种流体不仅是可取的,而且是必不可少的。
幸运的是,只要遵守一些预防措施,流体基质并不一定会妨碍将许多涉及颗粒物料的实验室甚至工业情况当作真正干燥的材料来处理。本节的目的是定义我们将在本书中发展的方法的有效性范围。出于严格的教学原因,我们首先讨论单个颗粒与其流体环境的相互作用。
Laminar Drag 层流阻力
Consider a spherical particle of radius $R$, mass $m$, and volumetric density $\rho_{b}$, moving at a velocity $v$ in a fluid of viscosity $\eta$. The surrounding fluid is contained within walls close to the central sphere, as shown in Figure l0(a). We wish to compare the kinetic energy of the particle with the energy loss due to the work done by the viscous forces existing within the fluid-forces which tend to slow down any movement.
考虑一个半径为 $R$、质量为 $m$、体积密度为 $\rho_{b}$ 的球形粒子,在粘度为 $\eta$ 的流体中以速度 $v$ 运动。如图 l0(a) 所示,周围的流体包含在靠近中心球的壁内。我们希望比较粒子的动能和由于流体中存在的粘性力做功而损失的能量–粘性力往往会减慢任何运动。
A sphere moving in a fluid in a laminar or turbulent regime.
在层流或湍流状态下在流体中运动的球体。
To that end, we define a parameter $R_{l}$ (the subscript $l$ stands for laminar), which is simply a measure of the ratio of the kinetic energy of the particle and the work done by the viscous force over a characteristic length, which we take to be the radius $R$ of the sphere. This parameter will enable us to estimate the importance of viscous dissipation in relation to the kinetic energy.
为此,我们定义了一个参数 $R_{l}$(下标 $l$ 代表层流),它是粒子动能与粘性力在一个特征长度(我们认为是球体半径 $R$)上所做功之比。通过这个参数,我们可以估算出粘滞耗散与动能之间的重要关系。
Based on what every student has learned in fluid dynamics theory, we write
$$ R_{l} = \frac{mv^{2}}{2\int_{I}\eta\pi R^{2}(\partial v/\partial x)\mathrm{d}x} $$
where the integral in the denominator extends over the interstitial space $I$ around the particle.
根据每个学生所学的流体力学理论,我们写道
$$ R_{l} = \frac{mv^{2}}{2\int_{I}\eta\pi R^{2}(\partial v/\partial x)\mathrm{d}x} $$
其中,分母中的积分延伸至粒子周围的间隙空间 $I$。
It is not essential to work out this integral exactly. In order to get an order of magnitude for $R_{l}$, all we need to do is estimate this integral by considering that all the lengths entering into it are of the order of $R$. In that case, we find that the denominator is of the order of $10\pi\eta R^{2}v$, while the numerator is equal to $\frac{4}{3}\rho_{b}\pi R^{3}v^{2}$. Within these approximations, we find that
$$ R_{l}\approx\frac{\rho_{b}}{\eta}Rv. $$
精确计算这个积分并不重要。为了得到 $R_{l}$ 的数量级,我们只需考虑所有进入积分的长度都是 $R$ 的数量级,从而估算出这个积分。在这种情况下,我们会发现分母的数量级为 $10\pi\eta R^{2}v$,而分子等于 $\frac{4}{3}\rho_{b}\pi R^{3}v^{2}$。在这些近似值中,我们发现
$$ R_{l}\approx\frac{\rho_{b}}{\eta}Rv. $$
We might point out in passing that the problem could have been solved directly by using Stokes’s formula for the drag of a sphere. We also note that (2-1) bears a striking similarity to the standard expression for Reynolds’s number, which gives the ratio of convective flux to diffusive flux in a viscous fluid in motion.
我们可以顺便指出,这个问题可以直接用 Stokes 的球体阻力公式来解决。我们还注意到,(2-1) 与雷诺数的标准表达式极为相似,后者给出了运动中粘性流体的对流通量与扩散通量之比。
The reader will recall that Reynolds’s number is given by
$$ R_{e} = \frac{UL}{v} = \frac{\rho}{\eta}UL, $$
where $U$ is the velocity of the moving fluid, and $L$ is a length characteristic of that fluid. It is clear that $U$ and $L$ play a role similar to $v$ and $R$, respectively, in (2-1). The only difference between the two definitions is that in the case of a particle in motion in a fluid, it is the volumetric density of the particle that matters, rather than that of the moving fluid itself. With this restriction in mind, the number $R_{l}$ introduced above can be thought of simply as the Reynolds number for the problem at hand.
读者应该还记得 Reynolds 数的计算公式为
$$ R_{e} = \frac{UL}{v} = \frac{\rho}{\eta}UL $$
其中,$U$ 是运动流体的速度,$L$ 是该流体的长度特征。显然,$U$ 和 $L$ 在 (2-1) 中的作用分别类似于 $v$ 和 $R$。这两个定义的唯一区别在于,对于在流体中运动的粒子,重要的是粒子的体积密度,而不是运动流体本身的体积密度。考虑到这一限制,上面介绍的 $R_{l}$ 可以简单地看作是当前问题的 Reynolds 数。
It is useful to clarify the practical implications of (2-1) with the help of a nu- merical calculation that will put some orders of magnitude in perspective. If we consider a particle of silicate sand, of density $2.2\text{ g/cm}^{3}$ and diameter $1\text{ mm}$, moving at a speed of $1\text{ cm/s}$ in dry air, $R_{l}$ turns out to be roughly equal to $10^{4}$. This is a reassuring result which gives us confidence that it is perfectly legitimate to regard particles with this particular mass and speed as a dry granular.
我们可以通过一个直观的计算来说明(2-1)的实际意义。如果我们考虑一粒密度为 $2.2\text{ g/cm}^{3}$、直径为 $1\text{ mm}$、在干燥空气中以 $1\text{ cm/s}$ 的速度运动的硅酸盐沙粒,结果 $R_{l}$ 大致等于 $10^{4}$。这是一个令人欣慰的结果,它让我们确信,将具有这种特定质量和速度的粒子视为干燥颗粒是完全合理的。
If, on the other hand, we were to deal with a powder made of particles whose typical size is only $10\mu\text{m}$ (e.g., lycopodium powder), rather than the $1\text{ mm}$ used in the previous example, the number $R_{l}$ would decrease proportionately. It could easily get smaller than $10$, which would sound a warning that the viscosity of the surrounding fluid can no longer be safely ignored.
This simple calculation illustrates that, even in favorable experimental circumstances (such as a noncritical system of particles in motion), it is advisable to exercise caution. It is imperative to be alert to the possibility that our approximations for a dry granular medium may break down when interactions with the surrounding fluid are no longer negligible.
另一方面,如果我们要处理的是由典型尺寸仅为 $10\mu\text{m}$(如莱菔子粉)的颗粒组成的粉末,而不是上例中使用的 $1\text{mm}$,那么 $R_{l}$ 的数值就会成正比地减小。它很容易小于 $10$,这将发出警告,周围流体的粘度不能再被安全地忽略了。
这个简单的计算说明,即使在有利的实验条件下(如一个非关键的颗粒运动系统),也应谨慎行事。必须警惕的是,当与周围流体的相互作用不再可以忽略时,我们对干燥颗粒介质的近似可能会失效。
Before leaving this subject, the reader will appreciate that the situation is likely to be problematic in a fluid such as water, which has a coefficient of viscosity a hundred times larger than air. Even with particles as small as $1\text{ mm}$ in diameter, viscous interactions cannot be neglected in this case.
在离开这个话题之前,读者应当理解,在水这样的流体中,情况很可能会出现问题,因为水的粘度系数比空气大一百倍。在这种情况下,即使颗粒的直径只有 $1\text{mm}$,粘性相互作用也是不可忽视的。
Turbulent Drag 湍流阻力
Hydrodynamics taught us that, as soon as the relative speed of a particle in motion in a fluid matrix becomes sufficiently high, instabilities appear in the boundary layer between the fluid and the object in motion (Figure 10b). There is at that moment a transition from a laminar flow to one that is turbulent. We also know that the transition between the two regimes occurs for relative speeds of the order of a few $\text{cm/s}$ in dry air.
流体力学告诉我们,一旦流体基质中运动粒子的相对速度变得足够高,流体和运动物体之间的边界层就会出现不稳定现象(图 10b)。此时,层流会向湍流过渡。我们还知道,在干燥空气中,当相对速度为几 $\text{cm/s}$ 时,两种状态之间就会发生转换。
As it happens, most granular flows involve velocities that are precisely in that range. We can thus anticipate that, depending on the details of the circumstances, energy dissipation will be either laminar (directly linked to the viscosity of the fluid) or turbulent (related to the difference in dynamic pressure ahead of and behind the moving object).
恰好,大多数颗粒流动的速度都在这个范围内。因此,我们可以预见,根据具体情况,能量耗散要么是层流(与流体粘度直接相关),要么是湍流(与运动物体前后的动压差相关)。
Here again, we define a number $R_{t}$ (where the subscript $t$ now stands for turbulent) as the ratio of the kinetic energy to the work done by the opposing force of turbulence $F_{t}$ over the applicable characteristic length, which, as before, is typically of the order of the radius $R$ of the particle.
在此,我们再次定义一个数字 $R_{t}$(下标 $t$ 现在代表湍流),作为动能与湍流对力 $F_{t}$ 在适用特征长度上所做功的比值,如前所述,该特征长度通常与粒子半径 $R$ 的数量级相当。
This time around, though, the force $F_{t}$ is proportional to the frontal cross-sectional area $S$ of the particle, to the square of the relative speed $v$, and to a coefficient $k_{t}$ whose value is typically $0.24$ for a sphere. Specifically, we write
$$ F_{t} = k_{t}\frac{\rho_{0}v^{2}}{2}S, $$
where $\rho_{0}$ is the density of the fluid. We then find that the number $R_{t}$ is approximately equal to
$$ R_{t}\approx \frac{1}{k_{t}}\frac{\rho_{b}}{\rho_{0}}. $$
不过,这次的力 $F_{t}$ 与粒子的正面横截面积 $S$、相对速度 $v$ 的平方和系数 $k_{t}$ 成正比,对于球体来说,该系数的值通常为 $0.24$。具体来说,我们可以写成
$$ F_{t} = k_{t}\frac{\rho_{0}v^{2}}{2}S, $$
其中 $\rho_{0}$ 是流体的密度。然后,我们发现 $R_{t}$ 的数值近似等于
$$ R_{t}\approx \frac{1}{k_{t}}\frac{\rho_{b}}{\rho_{0}}. $$
This equation tells us that the number $R_{t}$ does not depend on the velocity (assuming that the regime is indeed turbulent). It also shows that the concept of dry granular, i.e., of a system of particles whose interactions with the surrounding fluid are negligible, is valid for sufficiently heavy particles such as grains of silicate sand moving through a gas such as air.
这个方程告诉我们,$R_{t}$ 的数值并不取决于速度(假定系统确实是湍流的)。它还表明,干燥颗粒的概念,即与周围流体的相互作用可以忽略不计的颗粒系统的概念,对于在空气等气体中运动的足够重的颗粒(如硅酸盐沙粒)是有效的。
In this case the number $R_{t}$ is greater than $10^{3}$, which justifies neglecting the effects of turbulent dissipation. Once again, we come to the conclusion that these effects can definitely not be ignored when the fluid is a liquid, in which case the ratio of the densities is about unity and hydrodynamic dissipation becomes predominant.
在这种情况下,数值 $R_{t}$ 大于 $10^{3}$,因此可以忽略湍流耗散的影响。我们再次得出结论,当流体为液体时,这些影响绝对不能被忽略,在这种情况下,密度比约为 1,流体动力耗散成为主导。
Granular Dendrites 颗粒树枝
We proceed next to discuss a rather spectacular and poorly understood phenomenon, which is due to an intriguing type of interaction between air and granular matter. Observed in granular dendrite experiments, it involves effects that have well-known counterparts in hydrodynamics when one fluid is injected into another more viscous one. Even the experimental configuration traditionally used with liquids (Hele-Shaw radial cell) is essentially duplicated to study granulars.
接下来,我们将讨论一种相当引人注目但不太理解的现象,这种现象是由于空气与颗粒物质之间一种有趣的相互作用而产生的。在颗粒树枝实验中观察到这种现象,它涉及到在流体注入另一种更粘稠的流体时,流体力学中已有的众所周知的对应效应。即使是传统上用于液体的实验配置(Hele-Shaw 径向电池)也基本上是为了研究颗粒而移植的。
The actual experiment goes as follows: A layer of fairly loose fine sand is placed between two glass plates. The upper plate has a hole in its center through which a hose is inserted to blow pressurized air into the granular material. When both the pressure and the flow are low, nothing happens; the sand behaves as an ordinary porous medium. But as the flow is increased, the grains of sands start moving around and a dendritic pattern develops with a fractal structure reminiscent of what is observed with non-Newtonian fluids. An example is shown in Figure 11.
实际实验过程如下:在两块玻璃板之间放置一层相当松散的细沙。上面的玻璃板中间有一个孔,通过这个孔可以插入一根软管,将加压空气吹入颗粒材料中。当压力和流量都较低时,什么也不会发生;沙子的行为就像普通的多孔介质。但随着流量的增加,沙粒开始四处移动,形成树枝状图案,其分形结构让人联想到在非牛顿流体中观察到的情况。图 11 显示了一个例子。
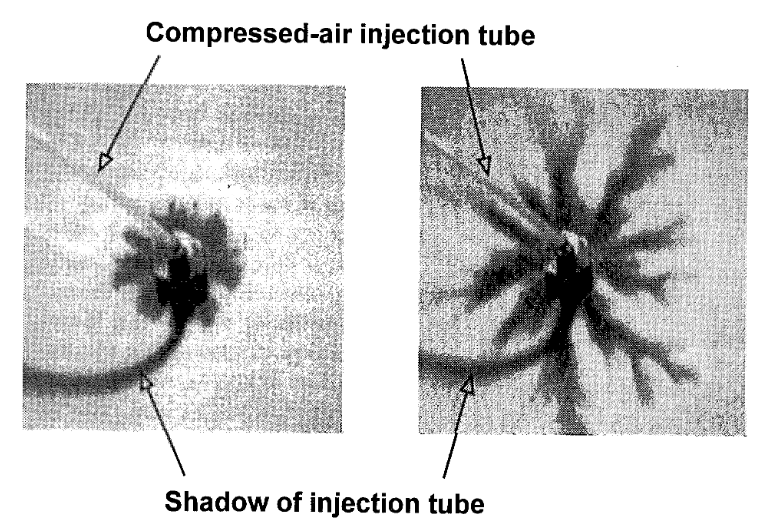
Growth of a dendritic pattern when air is injected into a confined granular medium. The photograph on the left shows the beginning of the process. The one on the right shows a well-developed pattern roughly $10\text{ cm}$ in diameter.
向封闭的颗粒介质中注入空气后,树枝状图案开始生长。左侧的照片显示了这一过程的开始。右边的照片显示的是一个直径约 $10$ 厘米的充分演化的图案。
The outcome of this experiment remains something of a mystery. Many questions come to mind. How can the sand grains move at all when they are confined in such a tight space between the glass plates, particularly since they must first expand before they can deform, as we will learn shortly? In other words, is the stack compact in the sense of the principle of dilatancy (see Section 3.1.3)? What determines the size of the dendrites? Can the granular medium be considered a viscous fluid?
这个实验的结果仍然是个谜。我想到了许多问题。当沙粒被限制在玻璃板之间如此狭小的空间里时,它们怎么可能移动,尤其是它们在变形之前必须先膨胀,这一点我们很快就会知道。换句话说,按照稀释原理(见第 3.1.3 节),堆栈是否紧凑?树枝状突起的大小由什么决定?能否将颗粒介质视为粘性流体?
Humidity, Electrostatic Interactions, and Other Perturbations 湿度、静电相互作用和其他扰动
There are plenty of indications, both in the laboratory and in industrial situations, that other perturbations can complicate things and tax our ability to model the behavior of “dry granulars” as we have defined them earlier. Ambient humidity, for instance, can cause serious disruptions by creating clumps of particles that are more or less mobile. We know from common experience that wet sand can be fairly cohesive, whereas dry sand crumbles apart readily.
无论是在实验室还是在工业环境中,都有大量迹象表明,其他扰动因素会使事情变得复杂,并削弱我们对 “干燥颗粒” 行为进行建模的能力,正如我们前面所定义的那样。例如,环境湿度会造成或多或少具有流动性的颗粒团块,从而造成严重干扰。根据常识,我们知道湿沙具有相当的凝聚力,同时干沙则很容易碎裂。
It is also intuitively obvious that the smaller the particles, the greater the perturbation-in the context of the present discussion-since capillary forces are then apt to be of the same order of magnitude as the gravitational forces that would otherwise largely determine the behavior of these objects. Once again, some systematic simplifications enable us to estimate how small the radius of spherical particles has to be in order for two of them to remain stuck together by a thin layer of water, against the action of gravity. The problem is illustrated in Figure 12.
同样直观明显的是,颗粒越小,扰动就越大–就目前的讨论而言–因为毛细管力的大小很可能与引力的大小相当,而引力在很大程度上决定了这些物体的行为。再次,通过一些系统性的简化,我们可以估算出球形颗粒的半径必须有多小,才能使两个颗粒在重力作用下被一层薄薄的水粘在一起。这个问题如图 12 所示。
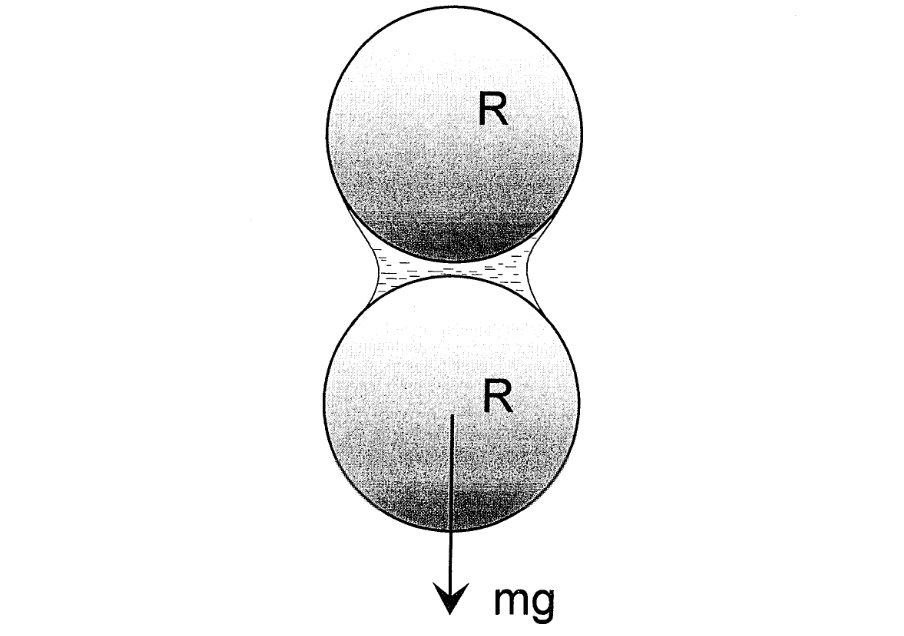
Spheres kept in contact by a liquid meniscus
通过液体半月板保持接触的球体
Calculating the capillary force that keeps two wet spheres in contact is far from trivial. Several methods have been proposed to avoid the difficulties associated with solving the Laplace-Young equation. The simplest one is known as the “pulley method,” because the contour of the meniscus is approximated by a pulley in the plane tangent to the two particles. The “pulley” has an inner radius $r_{1}$, while the outer radius (of the ridge) is $r_{2}$. This approach gives an expression for the capillary force in the form
$$ F_{c} = \pi\gamma_{lv}r_{2}\left(1 + \frac{r_{2}}{r_{1}}\right) $$
where $\gamma_{lv}$ is the surface tension at the air-liquid interface. We assume that, when the weight of the lower spherical particle is just equal to the capillary force, the radius of the liquid is some fraction a of the radius of the particles, or $r_{2}\approx\alpha R$, and the ratio $r_{2}/r_{1}$ is of the order of 5. This series of approximations leads to a result, correct within an order of magnitude, given by
$$ R \approx \sqrt{\frac{4\alpha\gamma_{lv}}{g\rho_{b}}}. $$
计算维持两个潮湿的球体相接触的毛细力远非易事。有几种方法被提出,以避免与解 Laplace-Young 方程相关的困难。最简单的方法被称为 “滑轮法”,因为 meniscus 的轮廓被近似为位于两个粒子的切平面内的一个滑轮。这个“滑轮”具有内半径 $r_{1}$,而外半径(轮脊的半径)为 $r_{2}$。这种方法给出了毛细力的表达式如下:
$$ F_{c} = \pi\gamma_{lv}r_{2}\left(1 + \frac{r_{2}}{r_{1}}\right) $$
其中 $\gamma_{lv}$ 是空气-液体界面的表面张力。我们假设当下方球形颗粒的重量刚好等于毛细力时,液体的半径为粒子半径的某一分数,或者 $r_{2}\approx\alpha R$,而比率 $r_{2}/r_{1}$ 大致为 5 次量级。这一系列的近似导致了以下结果,其精度在一个数量级内:
$$ R \approx \sqrt{\frac{4\alpha\gamma_{lv}}{g\rho_{b}}}. $$
When applied to glass beads ($\rho_{b} = 2.2\text{ g/cm}^3$) and water as the liquid ($\gamma_{lv} = 73 \times 10^{-3}\text{ N/m}$), the above expression suggests that the beads will remain stuck for diameters up to 1 mm when $\alpha = 1$. With a more modest amount of water ($\alpha = 0.01$), the diameter of the particles should not exceed $100 \mu\text{m}$.
This exercise highlights the need to control humidity levels when doing experiments with granular materials assumed to be dry. We may also conclude that industrial processes dealing with powders (particles smaller than $100 \mu\text{m}$) in open air are very likely not to conform to the type of physics presented in this book.
当应用于玻璃珠($\rho_{b} = 2.2\text{ g/cm}^3$)和作为流体的水($\gamma_{lv} = 73 \times 10^{-3}\text{ N/m}$)时,上述表达式表明,当 $\alpha = 1$时,玻璃珠的直径可达 $1\text{ mm}$。在水量较少的情况下($\alpha = 0.01$),颗粒的直径不应超过 $100 \mu\text{m}$。
这个练习强调了在对假定为干燥的颗粒材料进行实验时控制湿度的必要性。我们还可以得出这样的结论:在露天环境中处理粉末(颗粒小于 $100 \mu\text{m}$)的工业过程很可能不符合本书介绍的物理类型。
It is less straightforward to incorporate electrostatic interactions in a simple model, primarily because of the difficulty in quantifying even approximately the electric charges that develop on the surface of granulars in relative motion. It is somewhat easier to estimate them empirically on the basis of simple experiments, such as the following.
Drop a few steel balls, $1.5\text{ mm}$ in diameter, into a small plastic tube (Figure 13). Shake the tube and its contents vigorously and place it back vertically on a table. You will then notice that a certain number of balls remain stuck to the walls of the tube. The position of each of these balls in precarious equilibrium obviously depends on the position of its neighbors, since they all interact electrostatically.
在简单模型中加入静电相互作用就不那么简单了,这主要是因为, 即使是近似地量化相对运动中颗粒表面产生的电荷, 也仍然困难重重。根据简单的实验(如下面的实验)对其进行经验估算则更轻松一些。
将几个直径为 $1.5\text{ mm}$ 的钢球放入一个小塑料管中(图 13)。用力摇晃管子和里面的东西,然后把它垂直放回桌子上。这时你会发现,一定数量的小球仍然粘在管壁上。这些处于不稳定平衡状态的小球中,每个球的位置显然取决于其相邻球的位置,因为它们都会发生静电作用。
Small steel spheres suspended by electrostatic interactions on the walls of a plastic tube.
小钢球通过静电作用悬浮在塑料管壁上。
Knowing the weight of each steel sphere, and assuming that it is exactly offset by electrostatic repulsion, it is easy to calculate that each one carries an electric charge of the order of $3 \times 10^{-9} \text{C}$ (Coulomb), which corresponds approximately to $300\mu\text{C/kg}$, or a surface charge density of $4 \times 10^{-8}\text{ C/cm}^{2}$.
These numbers seem to agree with those usually observed in industry. Experience shows that organic materials are much less sensitive than minerals (by about a factor of 100), and that the amount of accumulated charge depends on the physical and chemical nature of the surfaces.
已知每个钢球的重量,并假定它恰好被静电斥力抵消,就可以很容易地计算出每个钢球所带电荷的数量级为 $3 \times 10^{-9}\text{C}$ (库仑),大约相当于 $300\mu\text{C/kg}$ 或表面电荷密度为 $4 \times 10^{-8}\text{ C/cm}^{2}$。
这些数字似乎与通常在工业中观察到的数字一致。经验表明,有机材料的敏感度比矿物低得多(约为 $100$ 倍),累积电荷量取决于表面的物理和化学性质。
Furthermore, as mentioned earlier, humidity minimizes this type of perturbation, although the actual mechanism is not entirely clear. Finally, the existence of these surface charges constitutes a danger in industrial facilities, which tend to store large quantities of dry grains (such as corn).
The reason is that they can trigger explosions of gases generated in silos by the decomposition of organic substances. A standard way to mitigate the risk in laboratories is to coat sensitive surfaces with antistatic sprays. This solution is unfortunately completely impractical on an industrial scale.
此外,如前所述,湿度可以将这种扰动降到最低,尽管实际机制并不完全清楚。最后,这些表面电荷的存在对储存大量干燥谷物(如玉米)的工业设施构成威胁。
原因是它们会引发筒仓中有机物质分解产生的气体爆炸。降低实验室风险的标准方法是在敏感表面喷涂抗静电喷雾剂。遗憾的是,这种解决方案在工业规模上完全不可行。
Classification of Granular Materials and Definitions 颗粒材料的分类和定义
It is useful to familiarize oneself with the terminology traditionally used in the field granular materials. The following definitions are taken from Brown and Richards, the authoritative source in such matters:
- A granular material is composed of discrete solids which are in contact most of the time. This specifically excludes objects such as fluidized beds, suspensions, and other loose materials in granular form. A parameter known as the fractional solid content of a granular medium is defined as the ratio of the volumetric density of the actual granular to the true intrinsic density of the solid constituent.
- A powder is a granular medium made of particles less than $100 \mu\text{ m}$ in diameter. It has become customary to make a further distinction between granular powders ($10$ to $100 \mu\text{m}$), superfine powders ($1$ to $10 \mu\text{m}$), and hyperfine powders ($0.1$ to $1 \mu\text{m}$).
- A granular solid is made of granules whose size ranges from $100$ to $3000 \mu\text{m}$.
- A broken solid is a granular material in which most particles are larger than 3 mm. Aggregates used to make ordinary concretes fall into that category, as do rock slides.
熟悉颗粒材料领域的传统术语非常有用。以下定义摘自 Brown 和 Richards 一书,该书在这方面具有权威性:
-
颗粒材料 是由大部分时间 接触 的离散固体组成。这明确排除了流化床、悬浮液和其他颗粒状松散材料等物体。颗粒介质的 部分固体含量 参数被定义为实际颗粒的体积密度与固体成分的真实内在密度之比。
-
粉末是由直径小于 $100 \mu\text{ m}$ 的颗粒组成的颗粒介质。人们已经习惯于进一步区分颗粒粉末($10$ 至 $100 \mu\text{m}$)、超细(superfine)粉末($1$ 至 $10 \mu\text{m}$)和超精细(hyperfine)粉末($0.1$ 至 $1 \mu\text{m}$)。
-
颗粒固体 由直径从 $100$ 到 $3000 \mu\text{m}$ 的颗粒组成。
-
破碎固体 是一种颗粒材料,其中大多数颗粒的直径大于 $3$ 毫米。用于制造普通混凝土的骨料属于这一类,岩石滑坡也属于这一类。
In light of these definitions and of our previous remarks, it should be clear that the physics of dry granular materials is limited in practice to granular solids and aggregates. Excluded are particulate systems such as powders, suspensions, or fluidized beds, in which interactions with the surrounding fluid are predominant.
根据这些定义和我们前面的论述,我们应该清楚,干燥 颗粒材料的物理学在实践中仅限于颗粒固体和聚集体。粉末、悬浮液或流化床等颗粒系统不在讨论范围内,因为在这些系统中与周围流体的相互作用占主导地位。
2.2 Interactions between Two Particles
Only recently was it recognized that the overall properties of dry granular media depend strongly on the fundamental mechanical characteristics of their constituents. The different possible behaviors (decompaction, vibration-induced fluidization, blockages by arching, various types of flows, all of which we will examine below), under the effect of external stimuli, can be traced in large part to the nature and importance of the micromechanical interactions of the particles, not only between themselves but also with the walls of the container.
直到最近,人们才认识到,干燥颗粒介质的整体特性在很大程度上取决于其成分的基本机械特性。在外部刺激作用下可能出现的不同行为(解压缩、振动引起的流化、拱形堵塞、各种类型的流动,我们将在下文中一一探讨),在很大程度上可以追溯到颗粒之间以及颗粒与容器壁之间微观机械相互作用的性质和重要性。
Stated differently, the modes of local energy dissipation determine in a fundamental way how granular materials behave. That said, we must also recognize that, as important as it may be to a detailed description of the relevant phenomena, the physics of interactions between solids in relative motion is far from being completely worked out.
换句话说,局部能量耗散模式从根本上决定了颗粒材料的行为方式。尽管如此,我们也必须认识到,尽管对相关现象的详细描述可能很重要,但相对运动中固体之间相互作用的物理学原理还远未完全阐明。
We will run repeatedly into this obstacle in our efforts to describe interactions between solids. It will be most obvious when we try to develop realistic computer simulations of these materials (see Chapter 6). A computer may be an ideal tool to handle N-body problems, but it does not absolve us from having to input the correct equations describing the relevant interactions, as we will become painfully aware of.
我们在描述固体之间的相互作用时,会反复遇到这种障碍。当我们试图对这些材料进行逼真的计算机模拟时,这种障碍最为明显(见第 6 章)。计算机可能是处理 $N$-body 问题的理想工具,但它并不能免除我们输入描述相关相互作用的恰当方程的责任,我们将痛苦地意识到这一点。
We now consider what happens when two objects come into contact, either suddenly or more gradually, as happens typically in granular media. Rather than immediately tackling the details of complex theories that are still in the process of being refined, we will instead intentionally limit our discussion to simple but extremely informative models, which will help us to understand two particularly important processes-friction and collisions between solids.
我们现在要考虑的是,当两个物体突然或逐渐接触时会发生什么,这通常发生在颗粒介质中。我们不会立即讨论仍在完善过程中的复杂理论的细节,而是有意将讨论限制在简单但信息量极大的模型上,这将有助于我们理解两个特别重要的过程–固体之间的摩擦和碰撞。
2.2.1 The Laws of Friction between Solids
The “macroscopic” laws governing the static and dynamic properties of two solids in contact are based strictly on experiments. They are remarkably simple and have stood the test of time with amazing durability. They have survived virtually untouched for almost five centuries, even though they describe phenomena that have yet to be fully understood on a fundamental level. Leonardo da Vinci gets credit for being the first to realize in the sixteenth century that, in order to get a solid to start sliding against another, it is necessary to apply to it a tangential force that is proportional not to the surface area in contact but, rather, to the force pressing the two objects together.
关于两个接触固体的静态和动态特性的 “宏观” 定律严格基于实验。它们非常简单,而且经受住了时间的考验,具有惊人的耐久性。尽管它们所描述的现象在基本层面上还没有被完全理解,但它们已经存活了近五个世纪,几乎从未被改动过。达芬奇(Leonardo da Vinci)在 16 世纪率先认识到,要使一个固体开始相对于另一个固体滑动,就必须对其施加切向力,这个切向力不是与接触表面积成正比,而是与将两个物体压在一起的力成正比。
This property was rediscovered in the seventeenth century by Guillaume d’ Amontons, and verified independently by La Hire at the insistence of the members of the French Academy of Sciences who were at first incredulous. In 1750, Leonhard Euler (1707-1783) introduced the concepts of static and dynamic friction. All these properties are summarized in a set of three fundamental laws. Interestingly, it was not until the second half of the twentieth century that they received a credible explanation in terms of interactions at the microscopic level.
十七世纪,纪尧姆-德-阿蒙通(Guillaume d’ Amontons)重新发现了这一特性,并在起初感到难以置信的法国科学院成员的坚持下,由拉希尔(La Hire)独立进行了验证。1750 年,欧拉(Leonhard Euler,1707-1783 年)提出了静摩擦和动摩擦力的概念。所有这些特性都被归纳为一组三个基本定律。有趣的是,直到二十世纪下半叶,它们才在微观层面的相互作用方面得到了可信的解释。
The Three Fundamental Laws of Solid Friction 固体摩擦的三个基本定律
Figure 14 depicts classic experiments that lead to the following conclusions:
- The force of traction required to set the system in motion is proportional to the total weight of the individual components $$ T = \mu\sum_{i}P_{i} = \mu P $$
- The force of traction $T$ is independent of the surface area of the solids in contact. In other words, a brick will start moving with the same force $T$ regardless of which of its faces it rests on.
- A distinction must made between static friction, when the solids are initially at rest, and dynamic friction, when the solids are already in motion and must be kept in motion at a constant speed. Each case is characterized by its own coefficient of friction-$\mu_{s}$ for static, and $\mu_{d}$ for dynamic. Euler demonstrated that $\mu_{d}\leq \mu_{s}$.
图 14 描述了得出以下结论的经典实验:
- 将系统置于运动所需的牵引力与各个组成部分的总重量成正比
$$ T = \mu\sum_{i}P_{i} = \mu P $$
-
牵引力 $T$ 与接触固体的表面积无关。换句话说,无论砖块的哪个面接触地面,它都会以相同的力 $T$ 开始运动。
-
必须区分静摩擦和动摩擦,当固体最初静止时,静摩擦系数为 $\mu_{s}$,当固体已经运动并且必须以恒定速度保持运动时,动摩擦系数为 $\mu_{d}$。Euler 证明了 $\mu_{d}\leq \mu_{s}$。
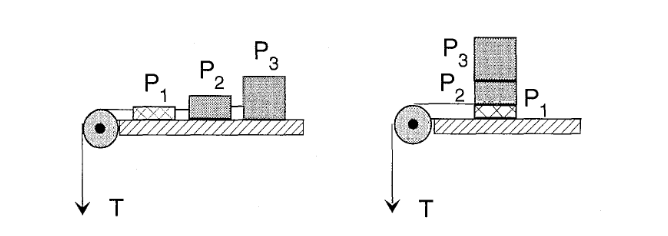
Leonardo da Vinci’s traction experiments. The force of traction $T$ necessary to set the disks P1, P2, and P3 is the same in both configurations.
达芬奇的牵引实验。在两种配置中,设置磁盘 P1、P2 和 P3 所需的牵引力 $T$ 是相同的。
Although no one individual can legitimately claim to have invented all three laws, it has become customary to refer to the entire set as Coulomb’s laws, because he used them in a now famous article on the properties of granular materials that ranks among the most frequently cited early references. We too will conform to this tradition.
We might note in passing that the coefficients of friction depend remarkably little on the nature of materials in contact. For instance, the coefficient $\mu$ is about 1 for friction between metals, 0.7 in the case of rocks, and 0.4 for paper. A rough explanation for this surprising result is provided by the model discussed next.
虽然没有一个人可以合法地声称自己发明了所有这三条定律,但人们习惯于将整套定律称为 Coulomb 定律,因为 Coulomb 在一篇关于颗粒材料性质的著名文章中使用了这些定律,这篇文章是最常被引用的早期参考文献之一。我们也将遵循这一传统。
我们可以顺便指出,摩擦系数与接触材料的性质关系不大。例如,金属之间的摩擦系数 $\mu$ 约为 $1$,岩石为 $0.7$,纸张为 $0.4$。接下来讨论的模型为这一惊人结果提供了一个粗略的解释。
A Microscopic Explanation 微观解释
Micrographs of the surface of ordinary solids such as metals reveal a ragged topography of the type schematically indicated in Figure 15. It is crucial to understand that Coulomb’s second law, which states that the force of traction required to set a solid object in motion is independent of the surface area in contact with the base, is justification enough for studying the physics of friction on the scale of a single protrusion (since the result does not depend on the number of such features).
普通固体(如金属)表面的显微照片显示了图 15 示意图所示的粗糙地形。Coulomb 第二定律指出,使固体物体运动所需的牵引力与与基体接触的表面积无关,理解这一点至关重要,它足以证明研究单个突起的摩擦物理学是合理的(因为结果并不取决于此类特征的数量)。
Schematic magnified view of the surface of a polished metal sample.
抛光金属样品表面的放大示意图。
These ragged features, whose typical size is of the order of $1 \mu\text{m}$, are so small that, even under weak stress conditions, the deformations they experience substantially exceed the elastic regime in which Hooke’s law remains valid (see some orders of magnitude in Section 2.2.2).
This implies that the protrusions in contact deform at constant pressure $p$ until they exactly offset the normal load force $N$ (normal in the sense of being perpendicular to the average plane of contact, as shown in Figure 16).
这些锯齿状特征的典型尺度为 $1 \mu\text{m}$,它们非常小,以至于即使在弱应力条件下,它们所经历的变形也大大超过了胡克定律生效的弹性机制(参见第 2.2.2 节中的一些数量级)。
这意味着接触的突起在恒定压力 $p$ 下会发生变形,直至完全抵消法向载荷力 $N$(如图 16 所示,法向是指垂直于平均接触平面)。
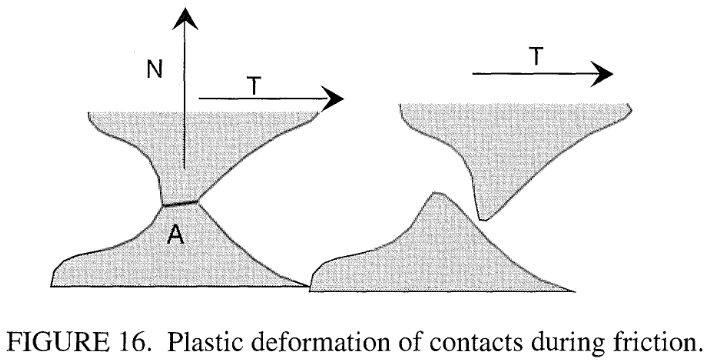
Plastic deformation of contacts during friction.
摩擦过程中触点的塑性变形
If $A$ is the surface area in contact, then the relation $N = pA$ holds when equilibrium has been reached. The effect of a sufficiently large tangential force $T$ is to separate the surfaces in contact. There is a constant $s$ which characterizes the ability of the material to resist this shearing action; it is given $T = sA$.
如果 $A$ 是接触表面的面积,那么当达到平衡时,关系式 $N = pA$ 成立。足够大的切向力 $T$ 会使接触表面分离。有一个常数 $s$,用于描述材料抵抗这种剪切作用的能力;它的值为 $T = sA$。
In this picture, the static friction coefficient $\mu_{s}$ defined previously can depend only on the physical constants of the materials in contact. Its value is
$$ \mu_{s} = \frac{T}{N} = \frac{s}{p} $$
在这种情况下,之前定义的静摩擦系数 $\mu_{s}$ 只取决于接触材料的物理常数。其值为
$$ \mu_{s} = \frac{T}{N} = \frac{s}{p} $$
As it happens, the constants $s$ and $p$ vary roughly in the same proportion for many different surfaces. In particular, metals are characterized by
$$ 0.6 \leq \frac{s}{p} \leq 1.2. $$
This model accounts for the tightly clustered range of values of $\mu_{s}$. It also explains the experimental observation that the contact regions between two solids deform slowly under the weight of the upper object, which is fully consistent with the behavior expected in the plastic regime. We shall present in Section 6.4 a more accurate description of these laws of friction in the context of numerical simulations.
对于许多不同的表面,常数 $s$ 和 $p$ 的变化比例大致相同。特别是,金属的特点是
$$ 0.6 \leq \frac{s}{p} \leq 1.2. $$
该模型解释了 $\mu_{s}$ 值的紧密聚集范围。它还解释了实验观察到的两个固体之间的接触区域在上部物体的重量作用下缓慢变形的现象,这与塑性状态下的预期行为完全一致。我们将在第 6.4 节中结合数值模拟对这些摩擦定律进行更精确的描述。
Gliding and Rotations: Frustrated Rotations 滑动和旋转: 受阻的旋转
The simplified stability conditions derived above apply to idealized situations. It would be risky to transpose them without any precautions to actual piles of granulates. A more careful scrutiny reveals a number of additional problems when trying to model what really goes on at contact points between two particles in a granular medium.
上述简化的稳定性条件适用于理想化的情况。如果不加任何预防措施就将其应用于实际的颗粒堆,那将是非常危险的。当试图模拟颗粒介质中两个颗粒之间接触点的实际情况时,更仔细的研究会发现一些额外的问题。
We will not reproduce here a detailed analysis that can be found in a number of classical mechanics texts dealing with solids in contact. We will, however, reemphasize a few concepts that are necessary for an understanding of the discussion to follow.
Figure 17 highlights some important quantities needed for a complete description of the motion of two rigid solids ($S$) and ($S^{\prime}$) around their point of contact $I$.
在此,我们不再重复许多经典力学著作中关于接触固体的详细分析。不过,我们将再次强调一些概念,这些概念对于理解接下来的讨论十分必要。
图 17 着重说明了完整描述两个刚性固体 ($S$) 和 ($S^{\prime}$) 围绕其接触点 $I$ 运动所需的一些重要量。
Geometry of two granules in contact.
两个接触颗粒的几何形状。
Let $\mathbf{N}$ and $\mathbf{T}$ be the force vectors normal and tangent to the plane $P$, which is itself tangent to the solids ($S$) and ($S^{\prime}$) at point $I$. The curves $L$ and $L^{\prime}$ are the loci of the contact points on each of the two solids as they rotate about each other. The motion of any point $M$ belonging to the solid ($S$) is described by a kinematic vector equation that gives its vector speed
$$ \mathbf{v}_{R}(M) = \mathbf{v}_{R^{\prime}}(I_{s}) + \mathbf{MI}\times\omega_{n} + \mathbf{MI}\times\omega_{t} $$
where $R$ and $R^{\prime}$ are frames of reference attached to solids ($S$) and ($S^{\prime}$), respectively.
令 $\mathbf{N}$ 和 $\mathbf{T}$ 分别为平面 $P$ 的法向量和切向量,平面 $P$ 本身与实体 ($S$) 和 ($S^{\prime}$) 相切于点 $I$。曲线 $L$ 和 $L^{\prime}$ 是两个实体绕彼此旋转时接触点的位置。属于固体($S$)的任意点 $M$ 的运动由运动矢量方程描述,该方程给出了其矢量速度
$$ \mathbf{v}_{R}(M) = \mathbf{v}_{R^{\prime}}(I_{s}) + \mathbf{MI}\times\omega_{n} + \mathbf{MI}\times\omega_{t} $$
其中,$R$ 和 $R^{\prime}$ 分别是隶属于固体($S$)和($S^{\prime}$)的参照系。
As written, the above equation describes the motion of point $M$ in the frame of reference of solid ($S^{\prime}$). For the purpose of simplification, we assume the solid ($S^{\prime}$) to be fixed. At any given instant, a generalized rotation (pivoting or rolling) is given as a sum of two orthogonal components
$$ \omega = \omega_{n} + \omega_{t}. $$
上式描述了点 $M$ 在固体($S^{\prime}$)参照系中的运动。为简化起见,我们假设固体($S^{\prime}$)是固定的。在任何给定的瞬间,广义的旋转(枢轴转动或滚动)都是两个正交分量的总和
$$ \omega = \omega_{n} + \omega_{t}. $$
The vector $\omega_{t}$ corresponds to a rotation in the plane of the figure, while $\omega_{n}$ describes spinning about a vertical axis. The dynamic equation written above includes three different types of motion between the solids involved:
- $\mathbf{v}_{g} = \mathbf{v}_{R^{\prime}}(I_{S})$ is the gliding velocity of ($S$) with respect to ($S^{\prime}$);
- $\mathbf{v}_{p} = \mathbf{MI}\times\omega_{n}$ is the angular speed of ($S$) with respect to ($S^{\prime}$) due to spinning;
- $\mathbf{v}_{r} = \mathbf{MI}\times\omega_{t}$ is the angular speed of ($S$) with respect to ($S^{\prime}$) due to rolling.
矢量 $\omega_{t}$ 对应的是图形平面内的旋转,而 $\omega_{n}$ 描述的是绕垂直轴的旋转。上面所写的动态方程包括所涉固体之间三种不同类型的运动:
- $\mathbf{v}_{g} = \mathbf{v}_{R^{\prime}}(I_{S})$ 是($S$)相对于($S^{\prime}$)的滑行速度;
- $\mathbf{v}_{p} = \mathbf{MI}\times\omega_{n}$ 是($S$)相对于($S^{\prime}$)由于旋转而产生的角速度;
- $\mathbf{v}_{r} = \mathbf{MI}\times\omega_{t}$ 是 ($S$) 由于滚动而相对于 ($S^{\prime}$) 的角速度。
Rolling without Gliding 无滑滚动
By definition, rolling without gliding implies $\mathbf{v}_{g} = \mathbf{v}_{R}(I_{s}) = 0$. The instantaneous axis of rotation is a straight line passing through point $I$ and aligned with the vector $\omega$. It describes a motion in which particles remain in contact by rolling on, rather than gliding past, one another. It typically applies to a string of roughened particles, acting somewhat like cogwheels, where the rotation of one member is readily transmitted to its neighbors. A three-dimensional arrangement of such particles is clearly a more complicated situation.
根据定义,无滑滚动意味着 $\mathbf{v}_{g} = \mathbf{v}_{R}(I_{s}) = 0$。瞬时旋转轴是一条通过点 $I$ 并与向量 $\omega$ 对齐的直线。它描述了一种运动,在这种运动中,粒子通过相互滚动而不是滑行来保持接触。它通常适用于一串粗糙的颗粒,其作用有点像齿轮,其中一个成员的旋转很容易传递给其相邻的成员。这种颗粒的三维排列情况显然更为复杂。
As depicted in Figure 18, the opposite rotation of two of the particles leaves the state of the third undetermined. In the case of a compacted pile, where all the particles are in intimate contact, it is easy to envision that rotations might in fact be entirely inhibited.
This phenomenon is sometimes referred to as frustration in some other branches of physics (such as spin glasses). This condition appears to prevail in convection movements (see Chapter 3). We will discuss these basic concepts in more depth when we study the fragmentation of piles in Section 3.2.4.
如图 18 所示,两个颗粒的反向旋转使得第三个颗粒的状态无法确定。在压实堆积的情况下,所有颗粒都紧密接触,因此很容易设想旋转实际上可能完全被抑制。
在物理学的其他一些分支(如自旋玻璃)中,这种现象有时被称为 “阻挫"。对流运动中似乎也存在这种情况(见第 3 章)。我们将在第 3.2.4 节研究桩的碎裂时更深入地讨论这些基本概念。
Possible behaviors of three granules in contact.
三种颗粒接触时的可能行为。
Gliding without Rolling 无滚滑动
This situation applies to perfectly smooth or nearly frictionless particles. However, it is also possible to observe gliding without rolling in compact piles when rotations are precluded for geometric reasons, in which case, $\omega_{p} = \omega_{r} = 0$.
Under these conditions, the equilibrium of a string of particles simply involves Coulomb’s maximum angle given by $\theta=\tan^{-1}{(\mu_{s})}$. As depicted in Figure 18, two particles in contact will be able to glide on each other only if their common tangent is inclined by angle not exceeding $\theta$ with respect to the horizontal.
这种情况适用于完全光滑或几乎无摩擦的粒子。然而,当旋转因几何原因而被排除在外时,也有可能在压实堆积中观察到无滚滑动,在这种情况下,$\omega_{p} = \omega_{r} = 0$。
在这些条件下,粒子链的平衡只涉及 Coulomb 最大角,即 $\theta=\tan^{-1}{(\mu_{s})}$。如图 18 所示,只有当两个接触的粒子的共同切线相对于水平面的倾斜角不超过 $\theta$ 时,它们才能相互滑行。
A complete analysis requires a knowledge of the forces pressing the particles together. As mentioned above, these forces contribute to the static equilibrium of the overall configuration and generate tangential friction forces. Such calculations have been carried out to study the stability of arches, a topic we will address in Section 3.1.1. We will encounter several practical applications of this remark.
完整的分析需要了解将粒子压在一起的力。如上所述,这些力有助于整体结构的静态平衡,并产生切向摩擦力。我们在第 3.1.1 节中将讨论桥型的稳定性问题,我们在研究桥型的稳定性时也进行过此类计算。我们将在实际应用中遇到一些类似的问题。
Transition from One Regime to the Other 从一个状态到另一个状态的转变
Rotation, pivoting, or gliding of one particle in contact with another or several others can be analyzed by writing down the general equations of mechanics of solids in contact. In conformance with the laws of dry friction reviewed above, whether gliding is allowed or not will be determined by the ratio of the normal component $\mathbf{N}$ of the reaction force $\mathbf{R}$ at the point of contact between the solids to the tangential component $\mathbf{T}$ along the particle’s trajectory.
一个质点与另一个或几个质点接触时的旋转、转动或滑动可以通过写下接触固体力学的一般性方程来分析。根据上述干燥摩擦定律,是否允许滑动将取决于固体接触点处反作用力 $\mathbf{R}$ 的法向分量 $\mathbf{N}$ 与沿质点轨迹的切向分量 $\mathbf{T}$ 的比值。
Coulomb’s maximum angle $\theta = \tan^{-1}{(\mu_{s})}$ defines a cone whose axis is perpendicular to the tangent plane at the point of contact. The motion will proceed without gliding as long as $\mathbf{R}$ is contained within this cone, known as the “friction cone,” and with~~~out~~~ gliding otherwise.
Coulomb 最大角 $\theta = \tan^{-1}{(\mu_{s})}$ 定义了一个锥体,其轴线垂直于接触点的切平面。只要 $\mathbf{R}$ 包含在这个被称为 “摩擦锥 “的圆锥内,运动就不会滑行,否则就~~~不~~~会滑行。
注: 这里的 without 疑似是作者笔误
Stick-Slip Motion 粘滑运动
We will deal on several occasions (see in particular Sections 3.1.1 and 4.2.2) with a type of motion frequently observed in situations involving dry friction. The motion in question is known as stick-slip. It typically results from interactions between particles that are subject to the Coulomb-Euler laws of friction and also exhibits an elastic behavior. Given that the granular materials we are specifically interested in often conform to both requirements simultaneously, it should come as no surprise that the stick-slip mechanism is commonly observed in granular matter. Although we will have an opportunity to give a more general treatment of the phenomenon later (see Section 4.2.2), we nevertheless introduce here a simplistic but instructive description. It is based on the model illustrated in Figure 19.
在干燥摩擦情况下, 我们将屡次讨论(特别是在第 3.1.1 节和第 4.2.2 节)经常观察到的一种运动。这种运动被称为 粘滑。它通常是颗粒之间相互作用的结果,受 Coulomb-Euler 摩擦定律的影响,同时也表现出弹性行为。鉴于我们特别感兴趣的颗粒材料往往同时符合这两个要求,因此在颗粒物质中普遍观察到粘滑机制也就不足为奇了。虽然稍后我们将有机会对这一现象进行更全面的阐述(见第 4.2.2 节),但我们还是在此介绍一种简单但具有启发性的描述。它基于图 19 所示的模型。
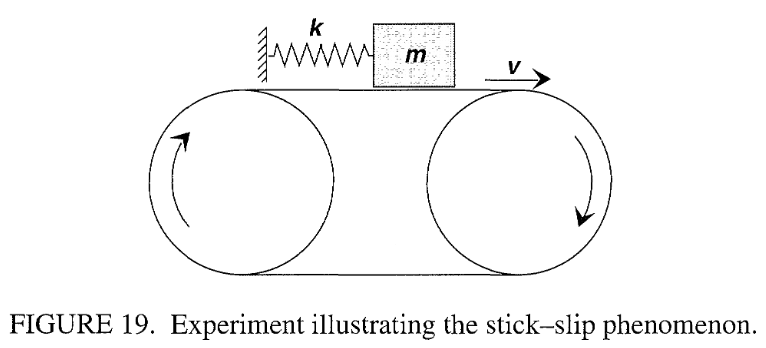
Experiment illustrating the stick-slip phenomenon.
说明粘滑现象的实验。
An object of mass $m$ is placed on a conveyor belt moving at a speed $v$. The object is also tied to a stationary post by a string of stiffness $k$. The friction between the object and the belt is characterized by coefficients $\mu_{s}$ (static) and $\mu_{d}$ (dynamic), such that $\mu_{d}\leq\mu_{s}$, in accordance with the Coulomb-Euler laws. For the sake of simplicity, we assume that $\mu_{d}$ is negligibly small.
质量为 $m$ 的物体被放置在以速度 $v$ 运动的传送带上。该物体还被一根劲度系数为 $k$ 的绳子绑在一根静止的柱子上。根据 Coulomb-Euler 定律,物体与传送带之间的摩擦系数分别为 $\mu_{s}$(静态)和 $\mu_{d}$(动态),即 $\mu_{d}\leq\mu_{s}$。为简单起见,我们假设 $\mu_{d}$ 小到可以忽略不计。
We start at time $t = 0$ with the spring in a state of rest, at which point its length is $x = x_{0}$. Because of dry friction, the object starts moving at a constant speed $v$. The horizontal component of the reaction associated with the friction opposes the traction of the spring, which we write as
$$ T = k(x - x_{0}) = kvt $$
从时间 $t = 0$ 开始,弹簧处于静止状态,此时长度为 $x = x_{0}$。由于干燥摩擦,物体开始以恒定速度 $v$ 运动。与摩擦力相关的反作用力的水平分量与弹簧的牵引力相反,我们将其写为
$$ T = k(x - x_{0}) = kvt $$
The uniform horizontal motion continues as long as Coulomb’s condition is verified, that is, as long as
$$ \left|\frac{T}{N}\right| = \frac{kvt}{mg} \leq \mu_{s}. $$
The condition is met for a duration $t\leq t_{1}$ such that $t_{1} = mg\mu_{s}/kv$. As soon as $t > t_{1}$, the force of friction gives way (suddenly becomes equal to 0), and the motion of the mass $m$ obeys the usual differential equation
$$ m\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}} = -k(x - x_{0}). $$
Its has a well-known solution, which can be written in terms of a parameter $\omega_{0} = \sqrt{k/m}$ as
$$ x(t) = x_{0} + A\sin{[\omega_{0}(t - t_{1}) + \alpha]} $$
where $A$ and $\alpha$ are integration constants obtained from boundary conditions at time $t = t_{1}$. These conditions are $x - x_{0} = vt_{1}$ and $\mathrm{d}^{2}x/\mathrm{d}t^{2} = v$, which leads to $vt_{1} = A\sin{(\alpha)}$,
$$ v = A\omega_{0}\cos{(\alpha)},\quad\tan{(\alpha)} = \omega_{0}t_{1},\quad A = v\sqrt{t_{1}^{2} + 1/\omega_{0}^{2}}. $$
只要 Coulomb 条件得到验证,即只要
$$ \left|\frac{T}{N}\right| = \frac{kvt}{mg} \leq \mu_{s}. $$
匀速水平运动就会持续下去. 当持续时间为 $t\leq t_{1}$ 时,条件满足,即 $t_{1} = mg\mu_{s}/kv$ 。只要 $t > t_{1}$,摩擦力就会消失(突然变为 0),质量 $m$ 的运动服从通常的微分方程
$$ m\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}} = -k(x - x_{0}). $$
它有一个众所周知的解,可以用参数 $\omega_{0} = \sqrt{k/m}$ 来表示
$$ x(t) = x_{0} + A\sin{[\omega_{0}(t - t_{1}) + \alpha]} $$
其中 $A$ 和 $\alpha$ 是从时间 $t = t_{1}$ 的边界条件得到的积分常数。这些条件是 $x - x_{0} = vt_{1}$ 和 $\mathrm{d}^{2}x/\mathrm{d}t^{2} = v$,这导致 $vt_{1} = A\sin{(\alpha)}$,
$$ v = A\omega_{0}\cos{(\alpha)},\quad\tan{(\alpha)} = \omega_{0}t_{1},\quad A = v\sqrt{t_{1}^{2} + 1/\omega_{0}^{2}}. $$
The motion is sinusoidal until time $t_{2}$ when the velocity of the object relative to the belt is zero. At that instant, static friction kicks in again. The time $t_{2}$ is given by one of the roots (the one that is different from $t_{2} = t_{1}$) of the equation
$$ \cos{[\omega_{0}(t_{2} - t_{1}) + \alpha]} = \cos{\alpha}. $$
This leads to $t_{2} = t_{1} + 2[(\pi-\alpha)/\omega_{0}]$. The length of the spring at that moment is
$$ x - x_{0} = A\sin{[\omega(t_{2} - t_{1}) + \alpha]} = -A\sin{(\alpha)}. $$
Once again, the object is dragged by the belt at constant speed $v$ until time $t_{3}$. The distance covered during the interval $t_{3} - t_{2}$ is $2A \sin{(a)}$. The complete periodic motion $x(t)$ is schematically depicted in Figure 20.
运动是正弦的,直到 $t_{2}$ 时物体相对于传送带的速度为零。此时,静摩擦力再次起作用。时间 $t_{2}$ 由方程的一个根(与 $t_{2} = t_{1}$ 不同的根)给出
$$ \cos{[\omega_{0}(t_{2} - t_{1}) + \alpha]} = \cos{\alpha}. $$
由此得出 $t_{2} = t_{1}+ 2[(\pi-\alpha)/\omega_{0}]$. 此时弹簧的长度为
$$ x - x_{0} = A\sin{[\omega(t_{2} - t_{1}) + \alpha]} = -A\sin{(\alpha)}. $$
在时间 $t_{3}$ 之前,物体再次被传送带以恒定速度 $v$ 拖动。在 $t_{3}- t_{2}$ 时间间隔内的距离为 $2A \sin{(a)}$。完整的周期运动 $x(t)$ 如图 20 所示。
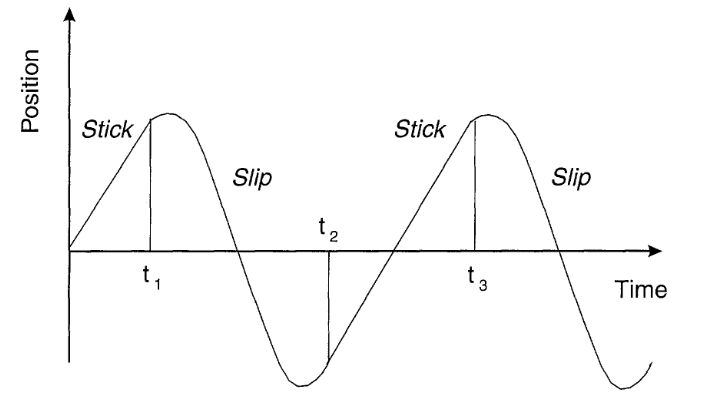
Dynamics of a periodic stick-slip motion. Straight-line segments (stick phase) are connected to portions of sinusoids (slip phase).
周期性 粘滑 运动的动力学。直线段(粘滞阶段)与正弦波段(滑移阶段)相连。
It is composed of straight-line segments joined by sinusoidal sections. The period $t_{0}$ is given by
$$ t_{0} = \frac{2}{\omega_{0}}(\pi - \alpha) + \frac{2A\sin{\alpha}}{v}. $$
它由正弦片段与直线段连接组成的。周期 $t_{0}$ 取值为
$$ t_{0} = \frac{2}{\omega_{0}}(\pi - \alpha) + \frac{2A\sin{\alpha}}{v}. $$
The amplitude is the same as that of the sinusoid. At low speed, the diagram becomes a saw-tooth made of a series of straight lines. In that case, $t_{1} = mg\mu_{s}/kv$. We might also point out that the value of the static friction coefficient $\mu_{s}$ can be determined by measuring the maximum amplitude of the motion. As a further exercise, the reader is encouraged to look at the shape of the function $F(v)$ which describes the friction force as a function of the speed of the belt, and to show that it has regions of negative slope (see Sections 2.3 and 4.2.2).
振幅与正弦波相同。在低速状态下,图表会变成由一系列直线组成的锯齿形。在这种情况下,$t_{1} = mg\mu_{s}/kv$。我们还可以指出,静摩擦系数 $\mu_{s}$ 的值可以通过测量运动的最大振幅来确定。作为进一步的练习,我们鼓励读者观察描述摩擦力的函数 $F(v)$ 的形状,它是传送带速度的函数,并证明它有负斜率区域(见第 2.3 节和第 4.2.2 节)。
This simplistic model can also explain the forced vibration of a violin string; because the bow is normally made of hair coated with colophane, its interaction with the string is a classic example of dry friction. In a more prosaic vein, stick-slip is responsible for the squeaking of poorly lubricated doors, the bucking of machine tools, and other similar phenomena.
这种简化模型也可以解释小提琴琴弦的受迫振动;因为琴弓通常是由涂有胶纸的毛发制成的,它与琴弦的相互作用就是典型的干燥摩擦。从更平实的角度看,润滑不良的门会发出吱吱声、机床会发生弯曲以及其他类似现象都是粘滑造成的。
2.2.2 Collisions and Deformations of Elastic Spheres
Frontal Elastic Collision 正面弹性碰撞
The frontal elastic collision of two spherical particles, illustrated in Figure 21, is extremely simple to analyze. In this particular case, the impact occurs along the axis passing through the center of each sphere, which means that the velocities are collinear. This is, of course, a highly improbable event with real granular solids, which most often behave as inelastic objects, subject to friction, and experiencing collisions at various angles. Nevertheless, the ideal case is useful to look at because it involves two fundamental tenets of classical mechanics-conservation of momentum and of kinetic energy.
两个球形颗粒的正面弹性碰撞(如图 21 所示)分析起来非常简单。在这种特殊情况下,撞击沿着穿过两球心的轴线进行,这意味着速度是平行的。当然,这在实际的颗粒状固体中是极不可能发生的,因为它们通常表现为非弹性物体,受到摩擦力的影响,并以各种角度发生碰撞。不过,这种理想情况还是值得研究的,因为它涉及到经典力学的两个基本原则–动量和动能守恒。
Two elastic spheres exchange momenta during a head-on collision.
两个弹性球体在正面碰撞过程中交换了动量。
Referring to the notation indicated in Figure 21, the speed after impact is given by
$$ u_{1} = \frac{m_{1} - m_{2}}{m_{1} + m_{2}}v_{1} + \frac{2m_{2}}{m_{1} + m_{2}}v_{2}. $$
参照图 21 所示下标,撞击后的速度为
$$ u_{1} = \frac{m_{1} - m_{2}}{m_{1} + m_{2}}v_{1} + \frac{2m_{2}}{m_{1} + m_{2}}v_{2}. $$
In actuality, collisions between real granulates always entail some loss of momentum and kinetic energy. Some fraction of the incident momentum is given up to the colliding particles by exciting sound waves propagating in their interior. In the process, a portion of the elastic energy stored in both particles is dissipated in the form of acoustic waves or phonons that relax by heating up the mass of both particles. A loss of kinetic energy can also result from a permanent deformation incurred during a collision. In any event, we observe experimentally that a ball hitting a vertical wall of infinite mass with a velocity $v$ rebounds with a smaller velocity $-\varepsilon_{p}\mathbf{v}$ (with $\varepsilon_{p}\leq 1$).
实际上,实际颗粒之间的碰撞总是会损失一些动量和动能。入射动量的一部分会通过激发在碰撞颗粒内部传播的声波传递给碰撞颗粒。在此过程中,储存在两个粒子中的部分弹性能量以声波或声子的形式耗散,声子通过加热两个粒子的质量而松弛。碰撞过程中产生的永久形变也会导致动能损失。无论如何,我们通过实验观察到,一个球以 $v$ 的速度撞击质量无限大的垂直墙壁后,会以更小的速度 $-\varepsilon_{p}\mathbf{v}$ 反弹($\varepsilon_{p}\leq 1$)。
To a first approximation, and in the case of frontal collision between two identical spheres, it is convenient to describe the velocity shortfall in the frame of reference of the center of gravity of the system by a matrix equation
$$ \begin{equation} \begin{bmatrix} u_{1} \\ u_{2} \end{bmatrix} = C_{1,2}\begin{bmatrix} v_{1} \\ v_{2} \end{bmatrix}= \begin{bmatrix} \frac{1-\varepsilon}{2} & \frac{1+\varepsilon}{2} \\ \frac{1+\varepsilon}{2} & \frac{1-\varepsilon}{2} \end{bmatrix}\begin{bmatrix} v_{1} \\ v_{2} \end{bmatrix} \end{equation}, $$
where $\varepsilon$ is called the “coefficient of elastic restitution.” Of course, $\varepsilon = 0$ for a completely inelastic collision (in which all the energy is dissipated in the collision), and $\varepsilon = 1$ for a perfectly elastic one.
作为一级近似,在两个完全相同的球体正面碰撞的情况下,用矩阵方程来描述系统质心系中的速度短差是很方便的
$$ \begin{equation} \begin{bmatrix} u_{1} \\ u_{2} \end{bmatrix} = C_{1,2}\begin{bmatrix} v_{1} \\ v_{2} \end{bmatrix}= \begin{bmatrix} \frac{1-\varepsilon}{2} & \frac{1+\varepsilon}{2} \\ \frac{1+\varepsilon}{2} & \frac{1-\varepsilon}{2} \end{bmatrix}\begin{bmatrix} v_{1} \\ v_{2} \end{bmatrix} \end{equation}, $$
其中 $\varepsilon$ 被称为 “弹性恢复系数”。当然,对于完全非弹性碰撞(在碰撞中, 全部能量都被耗散)$\varepsilon = 0$,对于完全弹性碰撞 $\varepsilon = 1$。
The collision of a ball with a plane of infinite mass can be described in a similar formalism by a matrix equation
$$ \begin{equation} \begin{bmatrix} u_{0} \\ u_{1} \end{bmatrix} = C_{0,1}\begin{bmatrix} v_{0} \\ v_{1} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 1 + \varepsilon_{p} & -\varepsilon_{p}\end{bmatrix}\begin{bmatrix} v_{0} \\ v_{1} \end{bmatrix} \end{equation}. $$
小球与无限大质量平面的碰撞也可以用类似的形式描述,即矩阵方程
$$ \begin{equation} \begin{bmatrix} u_{0} \\ u_{1} \end{bmatrix} = C_{0,1}\begin{bmatrix} v_{0} \\ v_{1} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 1 + \varepsilon_{p} & -\varepsilon_{p}\end{bmatrix}\begin{bmatrix} v_{0} \\ v_{1} \end{bmatrix} \end{equation}. $$
Such a phenomenological description ignores the details of the mechanics of the collision, particularly the modes of energy dissipation. As such, it must be used with some caution.
On the other hand, it is often sufficient to describe experimental observations, as we ourselves will realize when we discuss numerical simulations in Chapter 6. As long as we are prepared to adopt this approach, it is worthwhile to emphasize once again that $\varepsilon$ is truly a measure of the momentum loss of colliding particles.
这种唯象表述忽略了碰撞力学的细节,特别是能量耗散模式。因此,必须谨慎使用。
另一方面,它又通常足以描述实验的观察结果,在第 6 章讨论数值模拟时我们就会意识到这一点。只要我们准备采用这种方法,就值得再次强调,$\varepsilon$ 确实是对碰撞粒子动量损失的测量。
If $P$ and $P^{\prime}$ designate the momentum of the total system immediately before and immediately after impact, we may write in the frame of reference of the center of mass
$$ P = m_{12}(v_{1} - v_{2}),\\ P^{\prime} = m_{12}(u_{1} - u_{2}), $$
where $m_{12} = m_{1}m_{2}/(m_{1} + m_{2})$ is the reduced mass of the system of two colliding objects. It is straightforward to verify that (2-2) and (2-3) are indeed consistent with the definition of $\varepsilon$ in the form
$$ \varepsilon = -\frac{P^{\prime}}{P} = -\frac{u_{1}-u_{2}}{v_{1}-v_{2}}, $$
where the minus signs in front of the ratios account for the fact that the velocities reverse direction after the collision. The change in kinetic energy $\Delta E_{\text{kin}}$ after impact is easily shown to be given by
$$ \Delta E_{\text{kin}} = -\frac{1}{2}m_{12}(1-\varepsilon^{2})(v_{1} - v_{2})^{2}. $$
如果 $P$ 和 $P^{\prime}$ 分别表示撞击前和撞击后整个系统的动量,我们可以在质量中心的参照系中写道
$$ P = m_{12}(v_{1} - v_{2}),\\ P^{\prime} = m_{12}(u_{1} - u_{2}), $$
其中 $m_{12} = m_{1}m_{2}/(m_{1} + m_{2})$ 是两个碰撞物体系统的约化质量。很容易验证 (2-2) 和 (2-3) 与 $\varepsilon$ 的定义是一致的:
$$ \varepsilon = -\frac{P^{\prime}}{P} = -\frac{u_{1}-u_{2}}{v_{1}-v_{2}}, $$
其中分数前的负号考虑到了碰撞后速度反向的事实。碰撞后动能的变化量 $\Delta E_{\text{kin}}$ 可以很容易地表示为
$$ \Delta E_{\text{kin}} = -\frac{1}{2}m_{12}(1-\varepsilon^{2})(v_{1} - v_{2})^{2}. $$
Nonfrontal Elastic Collision and Rotation of Particles 非正面弹性碰撞和颗粒的旋转
As mentioned earlier, a frontal elastic collision, that is to say, the impact of rotationless particles along a path joining their centers, is an extremely improbable event that, to a first approximation, does not involve friction.
The reality is far more complex in granular media. It includes nonfrontal collisions and frictional effects giving rise to gliding and rolling motions that can impart angular momenta to neighboring particles. We proceed to give a somewhat simplified treatment of the problem. A more accurate description turns out to be extremely complicated.
As an introduction to a subsequent section in which we will outline a technique useful for numerical simulations of rotations, we develop next a classically mechanistic description of the gliding and rotation motions of two solids in contact.
如前所述,正面弹性碰撞,即无旋粒子沿着连接其中心的路径撞击,是一种极小概率事件,一级近似值不会涉及摩擦。
在颗粒介质中,实际情况要复杂得多。它包括非正面碰撞和摩擦效应,摩擦效应会引起滑动和滚动,从而将角动量传递给邻近的粒子。下面我们将对这一问题进行简化处理。更精确的描述将变得极其复杂。
在随后的章节中,我们将概述一种用于数值模拟旋转的技术,作为该章节的引言,我们接下来将对两个接触固体的滑行和旋转运动进行经典力学描述。
A Ball Thrown Against a Wall 球撞墙
We consider the simple problem of the collision between a spherical ball and a vertical wall. Let $v_{x}$ and $v_{y}$ be the components of the velocity of the center of mass of the ball, as shown in Figure 22, at the instant $t_{0}$ of impact. Let $\omega_{0}$ be its angular momentum just prior to impact.
We assume that the rotation vector is perpendicular to the plane of the figure. Under these conditions, it is intuitively obvious that the entire problem must retain the symmetry of the plane. Our goal is to determine the components $u_{x}$ and $u_{y}$ of the velocity immediately after the collision, as well as the final instantaneous rotation $\omega_{1}$. We designate by $X$ and $Y$ the components of the linear momentum at impact.
我们考虑一个球体与垂直墙壁碰撞的简单问题。设 $v_{x}$ 和 $v_{y}$ 为撞击前一瞬间 $t_{0}$ 球的质心速度分量,如图 22 所示。令 $\omega_{0}$ 为撞击前的角动量。
我们假设角速度矢量垂直于图中平面。在这些条件下,直观上很明显,整个问题必须保持平面的对称性。我们的目标是确定碰撞后的速度分量 $u_{x}$ 和 $u_{y}$,以及最终的瞬时旋转量 $\omega_{1}$。我们用 $X$ 和 $Y$ 表示碰撞时的线性冲量分量。
Geometry of a ball bouncing off a wall.
球从墙上弹起的几何学。
As indicated in Figure 22, we necessarily must have $v_{x}$, $u_{x}\geq 0$, and $X\geq 0$. If friction can be neglected in this simple experiment, then the solution is obviously identical with that obtained in the previous section. We simply write $u_{x} = -\varepsilon v_{x}$. The tangential component of $Y$ of the momentum $(X, Y)$ is zero, and the fundamental theorems of classical mechanics yield:
$$ \begin{aligned} m(u_{x} - v_{x}) &= X,\\ u_{y} &= v_{y},\\ \omega_{1} &= \omega_{2}. \end{aligned} $$
如图 22 所示,我们必须有 $v_{x}$、$u_{x}\geq 0$、$X\geq 0$。如果在这个简单的实验中可以忽略摩擦,那么解显然与上一节得到的解相同。我们可以简单地写成 $u_{x} = -\varepsilon v_{x}$。冲量 $(X, Y)$ 的切向分量 $Y$ 为零,经典力学基本定理由此得出:
$$ \begin{aligned} m(u_{x} - v_{x}) &= X,\\ u_{y} &= v_{y},\\ \omega_{1} &= \omega_{2}. \end{aligned} $$
If, on the other hand, we introduce a nonzero friction between the ball and the wall in the form of a single coefficient $\mu$, we must distinguish two separate cases.
另一方面,如果我们以单一系数 $\mu$ 的形式在球和壁之间引入非零摩擦力,我们就必须区分两种不同的情况。
- The Gliding Velocity Remains Positive for the Entire Duration of the Collision
In this case, the system of equations describing the exchange of momenta (linear and angular) reads
$$ \begin{aligned} m(u_{x} - v_{x}) &= X,\\ m(u_{y} - v_{y}) &= -\mu X,\\ \frac{2}{5}ma^{2}(\omega_{1}-\omega_{0}) &= a\mu X,\\ u_{x} &= -\varepsilon v_{x}, \end{aligned} $$
where $m$ is the mass of the ball (assumed solidly filled), and $a$ is its radius. It is immediately apparent that this system of four equations with four unknowns ($X, u_{x} , u_{y}, \omega_{1}$) can be solved if all relevant quantities before the collision are given and if the coefficients of friction $\mu$ and elastic restitution $\varepsilon$ are known. We leave this as an exercise, and focus our attention on the phenomenology of the collision, i.e., on the gliding and rotation motions of the ball during the collision.
- 滑行速度在整个碰撞过程中保持正值
在这种情况下,描述动量(线性冲量和角动量)交换的方程组为
$$ \begin{aligned} m(u_{x} - v_{x}) &= X,\\ m(u_{y} - v_{y}) &= -\mu X,\\ \frac{2}{5}ma^{2}(\omega_{1}-\omega_{0}) &= a\mu X,\\ u_{x} &= -\varepsilon v_{x}, \end{aligned} $$
其中 $m$ 是球的质量(假设为实心),$a$ 是球的半径。很明显,如果给出碰撞前的所有相关量,并且已知摩擦系数 $\mu$ 和弹性恢复系数 $\varepsilon$,则这个含有四个未知数($X, u_{x} , u_{y}, \omega_{1}$)的方程组可以解出。我们把这留作练习,并把注意力集中在碰撞的唯象理论上,即在碰撞过程中球的滑动和旋转。
We note first that the normal momentum $X = -mv_{x}(1 + \varepsilon)$ is indeed positive, as it should, since $v_{x}$ is negative. The final gliding velocity must also be positive, which is the case as long as
$$ \frac{7}{2}\mu(1 + \varepsilon) < \frac{v_{y} - a\omega_{0}}{-v_{x}}. $$
我们首先注意到法向动量 $X = -mv_{x}(1 + \varepsilon)$确实是正值,因为 $v_{x}$ 是负值。最终滑行速度也必须是正值,只要
$$ \frac{7}{2}\mu(1 + \varepsilon) < \frac{v_{y} - a\omega_{0}}{-v_{x}}. $$
- The Gliding Velocity Drops to Zero at any Time $t_{1}$ During the Collision 滑行速度在碰撞过程中的任何时间 $t_{1}$ 都会降为零
In that case, the general relations read
$$ \begin{aligned} m(u_{x} - v_{x}) &= X,\\ m(u_{y} - v_{y}) &= Y,\\ \frac{2}{5}ma^{2}(\omega_{1}-\omega_{0}) &= -aY,\\ u_{x} &= -\varepsilon v_{x},\\ u_{y} - a\omega_{1} &= 0. \end{aligned} $$
This time around, we have a system of five equations in five unknowns, which can easily be solved. We still have to verify that the linear momentum makes an angle less than $\tan^{-1}(\mu)$ and, in addition, that
$$ \frac{7}{2}\mu(1 + \varepsilon) > \frac{v_{y} - a\omega_{0}}{-v_{x}}. $$
The last two conditions turn out to be mutually exclusive. It follows that the behavior will be of one type or the other depending on the value of the friction coefficient $\mu$.
在这种情况下,一般关系如下
$$ \begin{aligned} m(u_{x} - v_{x}) &= X,\\ m(u_{y} - v_{y}) &= Y,\\ \frac{2}{5}ma^{2}(\omega_{1}-\omega_{0}) &= -aY,\\ u_{x} &= -\varepsilon v_{x},\\ u_{y} - a\omega_{1} &= 0. \end{aligned} $$
这一次,我们有了一个包含五个未知数的五次方程组,可以轻松求解。我们仍然需要验证线性动量的角度小于 $\tan^{-1}(\mu)$,此外,还需要验证
$$ \frac{7}{2}\mu(1 + \varepsilon) > \frac{v_{y} - a\omega_{0}}{-v_{x}}. $$
最后两个条件是相互排斥的。因此,根据摩擦系数 $\mu$ 的值,行为将是一种或另一种类型。
We may now ask ourselves whether these mutually exclusively situations are the only two possible outcomes. Is it at all possible for the gliding velocity to change sign during the interval $[t_{0},t_{1}]$ of the collision? If the answer is yes, the condition $|Y|<\mu X$ could still be verified without us being able to make any prediction whatsoever about the final value of $(u_{y} - a\omega_{1})$. The following reasoning gives the answer.
我们现在应当自问这两种互斥的情况是否是仅有的两种可能结果。在碰撞的区间 $[t_{0},t_{1}]$ 内,滑行速度是否有可能改变符号?如果答案是肯定的,那么条件 $|Y|<\mu X$ 仍然可以得到验证,而我们却无法对 $(u_{y} - a\omega_{1})$ 的最终值做出任何预测。下面的推理给出了答案。
Consider an instant $t\in[t_{0},t_{1}]$, and let $\eta$ and $\xi$ designate the components of the reaction force during impact. The equations of motion at that particular instant are
$$ \begin{aligned} m\frac{\mathrm{d}v_{x}}{\mathrm{d}t} &= \eta,\\ m\frac{\mathrm{d}v_{y}}{\mathrm{d}t} &= \xi,\\ \frac{2}{5}ma^{2}\frac{\mathrm{d}\omega}{\mathrm{d}t} &= -\xi a. \end{aligned} $$
考虑在一时刻 $t\in[t_{0},t_{1}]$,令 $\eta$ 和 $\xi$ 为碰撞过程中反作用力的分量。该时刻的运动方程为
$$ \begin{aligned} m\frac{\mathrm{d}v_{x}}{\mathrm{d}t} &= \eta,\\ m\frac{\mathrm{d}v_{y}}{\mathrm{d}t} &= \xi,\\ \frac{2}{5}ma^{2}\frac{\mathrm{d}\omega}{\mathrm{d}t} &= -\xi a. \end{aligned} $$
These give the following conditions concerning the gliding velocity
$$ m\frac{\mathrm{d}}{\mathrm{d}t}(v_{y} - a\omega) = \frac{7}{2}\xi. $$
As it turns out, the quantity $xi$, which is the tangential component of the reaction force during contact, has a sign opposite to that of $(v_{y} - a\omega)$.
这些条件给出了以下有关滑动速度的条件:
$$ m\frac{\mathrm{d}}{\mathrm{d}t}(v_{y} - a\omega) = \frac{7}{2}\xi. $$
事实证明,作为接触过程中反作用力切向分量的 $\xi$ 与 $(v_{y} - a\omega)$ 的符号 相反。
It follows that it can only decrease in magnitude. Should it reach zero at any time during the collision, it will remain zero up to the end. Stated in plain language, should the gliding speed happen to drop to zero at any time during a collision, the ball would then go on gliding for the remainder of the collision.
This simple argument shows that the two conditions considered previously are indeed mutually exclusive and that they are the only two possibilities. One or the other must prevail depending on the values of the friction coefficient $\mu$ and of the components of the incident velocity. The same distinction between two regimes will come up again when we study nonfrontal collisions between two spherical particles.
因此,它只能减小。如果它在碰撞过程中的任何时候达到零,那么直到碰撞结束,它都将保持为零。用通俗易懂的语言表达就是,如果在碰撞过程中的任何时候滑行速度恰好降为零,那么在碰撞的剩余时间内,小球将继续滑行。
这个简单的论证表明,之前考虑的两个条件确实是相互排斥的,而且它们是仅有的两种可能性。根据摩擦系数 $\mu$ 和入射速度分量的值,二者必居其一。当我们研究两个球形粒子之间的非正面碰撞时,会再次出现两种情况的区别。
Nonfrontal Collision Between Two Elastic Spheres with Friction 带摩擦的两个弹性球体之间的非正面碰撞
We have already introduced two fundamental parameters $\mu_{s}$ and $\mu_{d}$ to characterize interactions in the case of dry friction (Coulomb’s law), as well as the coefficient $\varepsilon$ which is a measure of the momentum loss. In addition to those, we now invoke another parameter, which we call the coefficient of tangential restitution, denoted $\beta$. Its effect is to dampen the tangential velocity at the point of contact as the particles recoil after colliding.
The need for such a coefficient and its precise definition will become clear as we further discuss the process of nonfrontal collisions. For now, let us simply consider two particles of diameter $d_{1}$ and $d_{2}$, and masses $m_{1}$ and $m_{2}$, respectively. The positions of the spheres are described by vectors $\mathbf{r}_{1}$ and $\mathbf{r}_{2}$. The geometry is depicted in Figure 23.
我们已经引入了两个基本参数 $\mu_{s}$ 和 $\mu_{d}$ 来描述干燥摩擦情况下的相互作用(Coulomb 定律),以及衡量动量损失的系数 $\varepsilon$。除此以外,我们现在还引用了另一个参数,我们称之为 切向回复系数, 记为 $\beta$。它的作用是抑制粒子碰撞后反冲时接触点的切向速度。
在我们进一步讨论非正面碰撞过程时,我们将清楚地了解对这一系数的需求及其精确定义。现在,让我们简单地考虑两个直径分别为 $d_{1}$ 和 $d_{2}$、质量分别为 $m_{1}$ 和 $m_{2}$ 的粒子。两球体的位置由向量 $\mathbf{r}_{1}$ 和 $\mathbf{r}_{2}$ 描述。几何图形如图 23 所示。
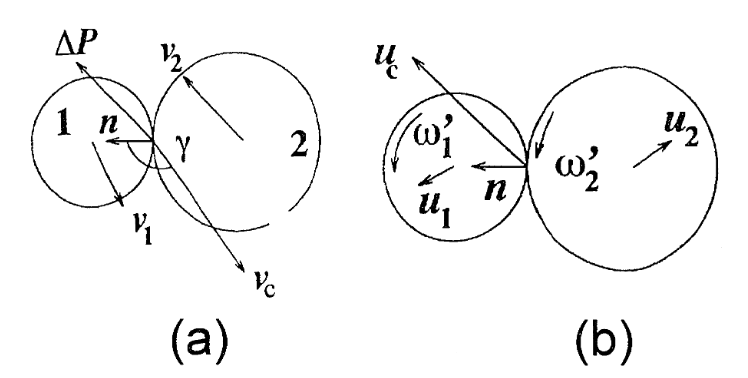
Two spheres (a) before and (b) after a nonfrontal collision. The parameters are defined in the text.
非正面碰撞前和碰撞后的两个球体(a)和(b)。参数定义见正文。
The unit vector associated with the normal to the plane of contact is denoted $\mathbf{n}$. It can be written as
$$ \mathbf{n} = \frac{\mathbf{r}_{1} - \mathbf{r}_{2}}{|\mathbf{r}_{1} - \mathbf{r}_{2}|}. $$
与接触平面法线相关的单位矢量用 $\mathbf{n}$ 表示。可以写成
$$ \mathbf{n} = \frac{\mathbf{r}_{1} - \mathbf{r}_{2}}{|\mathbf{r}_{1} - \mathbf{r}_{2}|}. $$
The relative velocity of the two particles at the point of contact is given by
$$ \mathbf{v}_{c} = \mathbf{v}_{1} - \mathbf{v}_{2} - \left(\frac{d_{1}}{2}\omega_{1} + \frac{d_{2}}{2}\omega_{2}\right)\times\mathbf{n}, $$
where $\mathbf{v}_{i}$ and $\omega_{i}$ are the translation and rotation velocities, respectively, of particle $i$ before the collision. Note that the magnitude of the relative speed $|\mathbf{v}_{c}|$ increases when the individual velocities point in opposite directions and when the rotation vectors of these particles point in the same direction.
两个粒子在接触点的相对速度为
$$ \mathbf{v}_{c} = \mathbf{v}_{1} - \mathbf{v}_{2} - \left(\frac{d_{1}}{2}\omega_{1} + \frac{d_{2}}{2}\omega_{2}\right)\times\mathbf{n}, $$
其中 $\mathbf{v}_{i}$ 和 $\omega_{i}$ 分别是碰撞前粒子 $i$ 的平移速度和角速度。请注意,当单个速度指向相反方向,而这些粒子的旋转矢量指向相同方向时,相对速度 $|\mathbf{v}_{c}|$ 的大小会增大。
The velocity $\mathbf{v}_{c}$ has a normal component $\mathbf{v}_{c}^{(n)} = (\mathbf{v}_{c}\cdot\mathbf{n})\mathbf{n}$, while its tangential component is $\mathbf{v}_{c}^{(t)} = \mathbf{v}_{c} - \mathbf{v}_{c}^{(n)}$. The vector $\mathbf{v}_{c}^{(t)}$ defines a unit tangential vector such that $\mathbf{t} = \mathbf{v}_{c}^{(t)}/|\mathbf{v}_{c}^{(t)}|$. The angle of impact $\gamma$ is defined as the angle between the normal $\mathbf{n}$ and the relative velocity $\mathbf{v}_{c}$, and is such that $y\in[\pi/2, \pi]$. Figure 23(a) shows the situation of the two colliding particles in the particular case when $\omega_{1} = \omega_{2} = 0$.
速度 $\mathbf{v}_{c}$ 有一个法向分量 $\mathbf{v}_{c}^{(n)} = (\mathbf{v}_{c}\cdot\mathbf{n})\mathbf{n}$ 、而其切向分量为 $\mathbf{v}_{c}^{(t)} = \mathbf{v}_{c} - \mathbf{v}_{c}^{(n)}$。矢量 $\mathbf{v}_{c}^{(t)}$ 定义了一个单位切向矢量,即 $\mathbf{t} = \mathbf{v}_{c}^{(t)}/|\mathbf{v}_{c}^{(t)}|$。撞击角 $\gamma$ 被定义为法线 $\mathbf{n}$ 与相对速度 $\mathbf{v}_{c}$ 之间的夹角,并且使得 $y\in[\pi/2, \pi]$。图 23(a) 显示了两个碰撞粒子在 $\omega_{1} = \omega_{2} = 0$ 的特殊情况下的情形。
在中文语境下, 我们常用 $\tau$ 表示切向
We now consider what happens to the kinetic momentum during the collision, using the same convention as before, namely that $\mathbf{u}_{i}$ designates the speed following the collision. We have
$$ \Delta\mathbf{P} = m_{1}(\mathbf{u}_{1} - \mathbf{v}_{1}) = -m_{2}(\mathbf{u}_{2} - \mathbf{v}_{2}). $$
The normal component of $\Delta\mathbf{P}$ has no effect on the angular rotation speed, but the tangential component does. By creating a torque on the arm defined by the vector $-(d_{1}/2)\mathbf{n}$, the change in momentum $\Delta\mathbf{P}$ causes a change in angular momentum such that
$$ -\mathbf{n}\times\Delta\mathbf{P} = \frac{2I}{d}(\omega^{\prime} - \omega), $$
where $I$ is the moment of inertia with respect to the center of the particle and $\omega^{\prime}$ is the unknown angular rotation speed after the collision. It should be appreciated that (2-5) indicates that the change in angular momentum is the same for both particles. Figure 25(b) depicts the situation after impact.
现在我们考虑碰撞过程中动量的变化,使用与之前相同的约定,即 $\mathbf{u}_{i}$ 表示碰撞 后的 速度。我们有
$$ \Delta\mathbf{P} = m_{1}(\mathbf{u}_{1} - \mathbf{v}_{1}) = -m_{2}(\mathbf{u}_{2} - \mathbf{v}_{2}). $$
$\Delta\mathbf{P}$ 的法向分量对角旋转速度没有影响,但切向分量有。通过在矢量 $-(d_{1}/2)\mathbf{n}$ 定义的力臂上产生力矩,动量变化量 $\Delta\mathbf{P}$ 会导致角动量的变化,即
$$ -\mathbf{n}\times\Delta\mathbf{P} = \frac{2I}{d}(\omega^{\prime} - \omega), $$
其中 $I$ 是相对于粒子中心的转动惯量,$\omega^{\prime}$ 是碰撞后的(未知)角速度。应该理解, (2-5)表明两个粒子的角动量变化是相同的。图 25(b) 描述了碰撞后的情况。
If $\Delta\mathbf{P}$ is known, it is possible to calculate all relevant velocities following the collision with the help of (2-4) and (2-5). The results are
$$ \begin{aligned} \mathbf{u}_{1} &= \mathbf{v}_{1} + \frac{\Delta\mathbf{P}}{m_{1}},\\ \mathbf{u}_{2} &= \mathbf{v}_{2} - \frac{\Delta\mathbf{P}}{m_{2}},\\ \omega_{1}^{\prime} &= \omega_{1} - \frac{d_{1}}{2I_{1}}\mathbf{n}\times\Delta\mathbf{P},\\ \omega_{2}^{\prime} &= \omega_{2} - \frac{d_{2}}{2I_{2}}\mathbf{n}\times\Delta\mathbf{P}. \end{aligned} $$
The reader will recall the definition of $\varepsilon$, given by
$$ \mathbf{u}_{c}^{(n)} = -\varepsilon\mathbf{v}_{c}^{(n)}, $$
which relates the translation velocities before and after the collision. Equa- tion (2-6) applied to the normal component of the sum $\Delta\mathbf{P}/m_1 + \Delta\mathbf{P}/m_{2}$ allows us to calculate the normal component of the change in linear momentum, giving the result
$$ \Delta\mathbf{P}^{(n)} = -m_{12}(1 + \varepsilon)\mathbf{v}_{c}^{(n)}, $$
where, as before, $m_{12}$ is the reduced mass of the system composed of $m_{1}$ and $m_{2}$.
如果已知 $\Delta\mathbf{P}$ ,就可以借助 (2-4) 和 (2-5) 计算碰撞后的所有相关速度。结果如下
$$ \begin{aligned} \mathbf{u}_{1} &= \mathbf{v}_{1} + \frac{\Delta\mathbf{P}}{m_{1}},\\ \mathbf{u}_{2} &= \mathbf{v}_{2} - \frac{\Delta\mathbf{P}}{m_{2}},\\ \omega_{1}^{\prime} &= \omega_{1} - \frac{d_{1}}{2I_{1}}\mathbf{n}\times\Delta\mathbf{P},\\ \omega_{2}^{\prime} &= \omega_{2} - \frac{d_{2}}{2I_{2}}\mathbf{n}\times\Delta\mathbf{P}. \end{aligned} $$
读者应该还记得 $\varepsilon$ 的定义,即
$$ \mathbf{u}_{c}^{(n)} = -\varepsilon\mathbf{v}_{c}^{(n)}, $$
它将碰撞前后的平移速度联系起来。将公式 (2-6) 应用于总和 $\Delta\mathbf{P}/m_1 + \Delta\mathbf{P}/m_{2}$ 的法向分量,我们就可以计算出线性动量变化的法向分量,从而得到结果
$$ \Delta\mathbf{P}^{(n)} = -m_{12}(1 + \varepsilon)\mathbf{v}_{c}^{(n)}, $$
如前所述,$m_{12}$ 是由 $m_{1}$ 和 $m_{2}$ 所组系统的约化质量。
Coulomb’s law establishes a relation between the normal and tangential components of $\Delta\mathbf{P}$, namely $|\Delta\mathbf{P}^{(t)}| = \mu|\Delta\mathbf{P}^{(n)}|$. Since collisions are always dissipative, the vector $\Delta\mathbf{P}^{(t)}$ must be aligned along $-\mathbf{t}$. We can thus write
$$ \Delta\mathbf{P}^{(t)} = \mu m_{12}(1 + \varepsilon)v_{c}\cos{(\gamma)}\mathbf{t}, $$
where we have $v_{c}^{(n)} = -v_{c}\cos{(\gamma)}$, since $\cos{\gamma}$ is always negative. We also have the relation $\mathbf{t} = \mathbf{v}_{c}^{(t)}/[v_{c}\sin{(\gamma)}]$. Combining (2-7) and (2-8) yields an expression for the change in momentum $\Delta\mathbf{P}$
$$ \Delta\mathbf{P} = m_{12}(1 + \varepsilon)[\mu\mathbf{v}_{c}^{(t)}\cot{(\gamma)} - \mathbf{v}_{c}^{(n)}]. $$
Coulomb 定律在 $\Delta\mathbf{P}$ 的法向分量和切向分量之间建立了一种关系,即 $|\Delta\mathbf{P}^{(t)}| = \mu|\Delta\mathbf{P}^{(n)}|$ 。由于碰撞总是耗散的,所以矢量 $\Delta\mathbf{P}^{(t)}$ 必须沿着 $-\mathbf{t}$ 对齐。因此,我们可以写成
$$ \Delta\mathbf{P}^{(t)} = \mu m_{12}(1 + \varepsilon)v_{c}\cos{(\gamma)}\mathbf{t}, $$
其中我们有 $v_{c}^{(n)} = -v_{c}\cos{(\gamma)}$,因为 $\cos{\gamma}$ 总是负值。我们还有一个关系 $\mathbf{t} = \mathbf{v}_{c}^{(t)}/[v_{c}\sin{(\gamma)}]$。结合 (2-7) 和 (2-8) 可以得到动量变化的表达式 $\Delta\mathbf{P}$
$$ \Delta\mathbf{P} = m_{12}(1 + \varepsilon)[\mu\mathbf{v}_{c}^{(t)}\cot{(\gamma)} - \mathbf{v}_{c}^{(n)}]. $$
The Tangential Restitution Coefficient 切向恢复系数
It is interesting to consider what happens in the case of a central collision, which corresponds to $\gamma\rightarrow\pi$. Since $\cot{(\gamma)}\rightarrow -\infty$, the change in momentum $\Delta\mathbf{P}$ would diverge to infinity, which is physically impossible.
The equations we have just derived describe all collisions, including tangential ones, on the basis of Coulomb’s law and the coefficient of elastic restitution, and nothing else. On closer scrutiny, though, there is another important physical mechanism that has been ignored in this description.
有趣的是,考虑一下对心碰撞的情况会发生什么,它对应于 $\gamma\rightarrow\pi$. 由于 $\cot{(\gamma)}\rightarrow -\infty$, 动量的变化 $\Delta\mathbf{P}$ 会发散到无穷大,这在物理上当然是不可能的。
我们刚刚推导出的方程描述了所有碰撞,包括切向碰撞,其基础是 Coulomb 定律和弹性恢复系数,除此之外别无其他。不过,仔细观察,我们还忽略了另一个重要的物理机制。
Specifically, at the moment of impact, the two interacting particles can either roll on each other without gliding, or the other way around. The possibility of a pivoting motion of one object on another (see Section 2.2.1) was not included in the simplified model presented above. Such a motion involves moments of inertia about the center or the rotation axis of the interacting particles.
具体来说,在撞击的瞬间,两个相互作用的粒子既可以相互滚动而不滑行,也可以反向滚动。在上述简化模型中,没有包含一个物体在另一个物体上旋转运动的可能性(见第 2.2.1 节)。这种运动涉及关于相互作用粒子的中心或旋转轴的转动惯量。
Rather than develop a more complex model to account for rolling without gliding (or vice versa), it is more expedient to heuristically generalize the existing model by introducing an additional parameter, which we will call the coefficient oftangential restitution, denoted $\beta$. It reflects the ability of a system to break the microscopic contact regions during a collision, thereby initiating a gliding regime. It can be shown that, under such conditions, (2-8) must be modified to a new form
$$ \Delta\mathbf{P} = -m_{12}(1 + \varepsilon)\mathbf{v}_{c}^{(n)} - \frac{2}{7}m_{12}(1 + \beta)\mathbf{v}_{c}^{(t)}. $$
与其开发一个更复杂的模型来解释无滑滚动(或反之亦然),不如通过引入一个附加参数来启发式地概括现有模型,我们将其称为 切向恢复系数, 表示为 $\beta$。它反映了系统在碰撞过程中打破微观接触区域,从而启动滑行机制的能力。可以证明,在这种条件下,(2-8)必须修改为一种新的形式:
$$ \Delta\mathbf{P} = -m_{12}(1 + \varepsilon)\mathbf{v}_{c}^{(n)} - \frac{2}{7}m_{12}(1 + \beta)\mathbf{v}_{c}^{(t)}. $$
The second term in (2-10) has the same form as the first, except for a factor of $\frac{2}{7}$ which comes about through the bias of the moment of inertia of a solidly filled sphere. In light of our previous remarks, the coefficient of tangential restitution $\beta$ must be equal to the smallest of two values $\beta_{0}$ or $\beta_{1}$ corresponding to one of two different regimes:
- Large values of the angle $\gamma(\gamma\geq\gamma_{0})$ correspond to a gliding contact, in which the contacts have been broken. In this case, the appropriate choice for $\beta$ is $\beta = \beta_{0}$, with $\beta_{0}\in[-1,+1]$.
- Small values of $\gamma(\gamma\leq\gamma_{0})$ correspond to a collision for which the interaction can be described in terms of dry friction and elastic restitution. In that case, the correct choice is $\beta = \beta_{1}$, with $\beta_{1} = -1 - \frac{7}{2}\mu(1 + \varepsilon)\cot{(\gamma)}$.
The angle $\gamma_{0}$ marks the dividing line between the two regimes, which occurs when $\beta_{0} = \beta_{1}$. The value of $\gamma_{0}$ is given by the equation
$$ -\tan{(\gamma_{0})} = \frac{7}{2}\mu\frac{1 + \varepsilon}{1 + \beta_{0}}. $$
(2-10) 中的第二项与第一项的形式相同,只是由于固体填充球体的惯性矩偏差而产生了一个 $\frac{2}{7}$ 的系数。根据我们前面的论述,切向复原系数 $\beta$ 必须等于两个值 $\beta_{0}$ 或 $\beta_{1}$ 中的最小值,这两个值对应于两种不同状态之一:
-
角度 $\gamma(\gamma\geq\gamma_{0})$ 的大值对应于滑动接触,其中的接触已经断开。在这种情况下,对 $\beta$ 的适当选择是 $\beta = \beta_{0}$,$\beta_{0}\in[-1,+1]$。
-
$\gamma(\gamma\leq\gamma_{0})$ 的小值对应于可以用干摩擦和弹性恢复来描述相互作用的碰撞。在这种情况下,正确的选择是 $\beta = \beta_{1}$, 其中 $\beta_{1} = -1 - \frac{7}{2}\mu(1 + \varepsilon)\cot{(\gamma)}$.
当 $\beta_{0} = \beta_{1}$ 时,角度 $\gamma_{0}$ 标志着两种状态的分界线。$\gamma_{0}$ 的值由以下方程给出:
$$ -\tan{(\gamma_{0})} = \frac{7}{2}\mu\frac{1 + \varepsilon}{1 + \beta_{0}}. $$
Reference [41] gives additional details on some practical aspects of the two modes of collision by considering the ratio of the normal and tangential collision velocities.
This all-or-nothing simplification makes it possible to pursue numerical calculations of situations involving nonfrontal collisions and rotations. We will discuss such models using rigid spheres to simulate particles undergoing multiple collisions (see Sections 3.2.4 and 6.1.2).
Before doing so, however, it is useful to first explore in more depth a number of problems associated with the mechanics of collisions. To that end, we proceed to calculate some orders of magnitude of a few phenomena occurring during the frontal collision of two spheres that can penetrate each other, as is almost always the case in the real world.
参考文献 [41] 通过考虑法向碰撞速度和切向碰撞速度之比,对两种碰撞模式的一些实际方面给出了更多细节。
这种全有或全无的简化使得对涉及非正面碰撞和旋转的情况进行数值计算成为可能。我们将讨论使用刚性球来模拟发生多次碰撞的粒子的模型(见第 3.2.4 节和第 6.1.2 节)。
不过,在此之前,我们有必要先更深入地探讨一些与碰撞力学相关的问题。为此,我们将着手计算两个球体正面碰撞时发生的一些现象的数量级,这两个球体可以相互穿透,在现实世界中几乎总是如此。
Penetration During Frontal Collision: Hertz’s Problem 正面碰撞时的穿透力:Hertz问题
Consider two identical spheres of radius $R$ and mass $M$, approaching each other at a relative velocity $v$, as shown in Figure 24. Hertz has shown that the elastic energy $E_{e}$ stored by two spheres deformed over a depth $h$ is given by
$$ E_{e} = \frac{1}{2}kh^{\frac{5}{2}}, $$
where the coefficient $k$ is defined as
$$ k = \frac{4\sqrt{2}}{15}\frac{E}{1-\sigma^{2}}\sqrt{R}. $$
The quantities $E$ and $\sigma$ entering in (2-11b) are Young’s modulus and Poisson’s coefficient, respectively. Upon impact, the initial kinetic energy is converted partly into a reduced kinetic energy and partly into stored elastic energy. Thus, we write
$$ Mv^{2} = kh^{\frac{5}{2}} + M\left(\frac{\mathrm{d}h}{\mathrm{d}t}\right)^{2}. $$
Interpenetration of two spheres during a frontal collision.
正面碰撞时两个球体的相互压缩。
如图 24 所示,考虑两个半径为 $R$、质量为 $M$ 的相同球体,以相对速度 $v$ 相互靠近。Hertz 已经证明,两个球体在深度 $h$ 上变形所储存的弹性能量 $E_{e}$ 由以下公式给出
$$ E_{e} = \frac{1}{2}kh^{\frac{5}{2}}, $$
其中系数 $k$ 的定义为
$$ k = \frac{4\sqrt{2}}{15}\frac{E}{1-\sigma^{2}}\sqrt{R}. $$
(2-11b) 中的 $E$ 和 $\sigma$ 分别是杨氏模量和泊松系数。撞击时,初始动能部分转化为降低后的动能,部分转化为储存的弹性能。因此,我们可以写成
$$ \frac{1}{2}Mv^{2} = \frac{1}{2}kh^{\frac{5}{2}} + \frac{1}{2}M\left(\frac{\mathrm{d}h}{\mathrm{d}t}\right)^{2}. $$
The velocity drops to zero when the two spheres have penetrated each other by a distance $h_{0}$. At that moment, $\mathrm{d}h/\mathrm{d}t = 0$, and we have
$$ h_{0} = \left(\frac{M}{k}\right)^{\frac{2}{5}}v^{\frac{4}{5}}. $$
The entire duration $\tau$ of the collision (penetration up to $h_{0}$ and recoil) is obtained by integrating (2-12)
$$ \tau = 2\int_{0}^{h_{0}}\frac{\mathrm{d}h}{\sqrt{v^{2} - (k/M)h^{\frac{5}{2}}}} = \frac{4\sqrt{\pi}\Gamma\left(\frac{2}{5}\right)}{5\Gamma\left(\frac{9}{10}\right)}\left(\frac{M^{2}}{k^{2}v}\right)^{\frac{1}{5}}. $$
Evaluating the gamma functions numerically leads to the result
$$ \tau = 2.94\left(\frac{M^{2}}{k^{2}v}\right)^{\frac{1}{5}}. $$
当两个球体相互压缩的距离为 $h_{0}$ 时,速度降为零。此时,$\mathrm{d}h/\mathrm{d}t = 0$,我们得到
$$ h_{0} = \left(\frac{M}{k}\right)^{\frac{2}{5}}v^{\frac{4}{5}}. $$
碰撞的整个持续时间 $\tau$ (压缩至 $h_{0}$ 并反冲)可通过积分 (2-12) 得到
$$ \tau = 2\int_{0}^{h_{0}}\frac{\mathrm{d}h}{\sqrt{v^{2} - (k/M)h^{\frac{5}{2}}}} = \frac{4\sqrt{\pi}\Gamma\left(\frac{2}{5}\right)}{5\Gamma\left(\frac{9}{10}\right)}\left(\frac{M^{2}}{k^{2}v}\right)^{\frac{1}{5}}. $$
对 Gamma 函数进行数值求值可得出以下结果:
$$ \tau = 2.94\left(\frac{M^{2}}{k^{2}v}\right)^{\frac{1}{5}}. $$
The exponent giving the dependence of $\tau$ on $v$ is only $\frac{1}{5}$. Thus, the duration of the impact between two particles is only a weak function of their initial relative velocity. For an order of magnitude calculation of the time involved, we consider the case of aluminum beads, 1.5 mm in diameter, moving toward each other at a speed of 5 cm/s. The constants relevant to aluminum are as follows
$$ \begin{aligned} E = 6\times10^{11} \text{ dynes/cm}^{2},\\ \sigma \approx 0.3,\\ k = 7\times 10^{10}(\text{cgs units}). \end{aligned} $$
Using these numbers, the result is $\tau = 5\times 10^{-6}\text{ s}^{-1}$.
给出 $\tau$ 与 $v$ 关系的指数仅为 $\frac{1}{5}$。因此,两个粒子之间的撞击持续时间只是它们初始相对速度的微弱函数。为了在数量级上计算所涉及的时间,我们考虑直径为 $1.5$ 毫米的铝珠以 $5$ 厘米/秒的速度相向运动的情况。与铝有关的常数如下:
$$ \begin{aligned} E &= 6\times10^{11} \text{ dynes/cm}^{2},\\ \sigma &\approx 0.3,\\ k &= 7\times 10^{10}(\text{cgs units}). \end{aligned} $$
使用这些数字,结果是 $\tau = 5\times 10^{-6}\text{ s}^{-1}$。
The purist might object that this derivation is based on a static analysis, which neglects two potentially important phenomena:
- The elasticity limit may be exceeded.
If so, the deformations are really plastic. With the help of (2-13), we may calculate the value of $h_{0}$ for the aluminum beads considered above. The result is $h_{0}\approx 2\mu\text{m}$, which implies a relative deformation-or strain-of $10^{-3}$. Aluminum is known to deform plastically for stresses of $20\text{ kg/mm}^{2}$, which corresponds to strains of $3\times 10^{-3}$-not very much larger than the number calculated above. The beads need only have a velocity two or three times larger to reach the plastic regime.
Most importantly, the deformation is of the order of the height of the surface roughness. In accordance with what was said in Section 2.2.1, the deformation of the surface protrusions during a collision is necessarily plastic. The implication is-and experiments confirm it-that the degree of polishing of the interacting objects plays a crucial role in the process of restitution during impact. We will see shortly an approach to describe the penetration of inhomogeneous spheres with a surface layer softer than the core.
- Part of the energy may be dissipated by exciting sound waves inside the solid beads.
As an example, we may calculate the time $\tau_{\text{ph}}$ it takes a phonon to complete a round trip across a sphere, knowing the propagation velocity $v_{\text{ph}}$. The result is $\tau_{\text{ph}} = 2R/v_{\text{ph}} = 0.15\text{ cm}/6 \times 10^{5}\text{ cm/s} = 2.5\times 10^{-7}\text{ s}$. In other words, there is plenty of time for several round trips during a typical collision. This effect constitutes a potentially important perturbation that in some cases may invalidate the model embodied in (2-12).
纯粹主义者可能会反对这种基于静态分析的推导,因为它忽略了两个潜在的重要现象:
- 可能超过弹性极限。
如果是这样,形变就真的是塑性形变了。借助 (2-13),我们可以计算出上述铝珠的 $h_{0}$ 值。结果是 $h_{0}\approx 2\mu\text{m}$ ,这意味着相对形变或应变为 $10^{-3}$。已知铝的塑性形变的应力为 $20\text{ kg/mm}^{2}$, 这相当于应变为的 $3\times 10^{-3}$ 倍–比上面计算的数字大得多。珠子只需要有两到三倍大的速度就能达到塑性状态。
最重要的是,变形量与表面粗糙度的高度相当。根据第 2.2.1 节所述,碰撞过程中表面突起的变形必然是塑性的。这意味着–实验也证实了这一点–相互作用物体的打磨程度在碰撞过程中的复原过程中起着至关重要的作用。我们很快就会看到一种描述表面层比核心层软的不均匀球体压缩情况的方法。
- 部分能量可能通过激发固体珠子内部的声波而耗散。
举例来说,我们可以计算一个声子在球体上完成一个来回所需的时间 $\tau_{\text{ph}}$,同时知道传播速度 $v_{\text{ph}}$。结果是 $\tau_{\text{ph}} = 2R/v_{\text{ph}} = 0.15\text{ cm}/6 \times 10^{5}\text{ cm/s} = 2.5\times 10^{-7}\text{ s}$ 。换句话说,在一次典型的碰撞中,都有足够的时间进行多次往返。这种效应构成了一个潜在的重要扰动,在某些情况下可能会使 (2-12) 所体现的模型失效。
Inhomogeneous Spheres: The Soft Crust Model 不均匀球体:软壳模型
As we have just noted, the quality and nature of the interface between two solids can raise serious questions about the validity of Hertz’s collision model. In the case of spherical particles whose surfaces are flawed or chemically altered, for instance by oxidation, de Gennes has proposed what might be described as a “soft crust” model. The idea is to consider that the sphere is wrapped in a thin layer of a softer material, of thickness $e$.
Young’s modulus $E_{e}$ of the outer layer is assumed to be smaller than the value $E$ prevailing in the interior. As long as the penetration is small ($h\ll e$), it is clear that the deformation due to impact remains confined to the outer layer of thickness $e$ and will not affect the core of the particle. The situation is illustrated in Figure 25.
正如我们刚才指出的,两个固体之间界面的品质和性质会对 Hertz 碰撞模型的有效性提出严重质疑。对于表面有缺陷或发生化学变化(如氧化)的球形颗粒,de Gennes 提出了一种可称为 “软壳” 的模型。其原理是将球体包裹在厚度为 $e$ 的较软材料薄层中。
假定外层的杨氏模量 $E_{e}$ 小于内部的普遍值 $E$。只要压缩很小($h\ll e$),显然撞击造成的变形将局限于厚度为 $e$ 的外层,而不会影响颗粒的核心。这种情况如图 25 所示。
Schematic ofthe zone affected during the penetration of two (a) homogeneous and (b) inhomogeneous spheres.
两个 (a) 均匀和 (b) 非均匀球体在压缩过程中受影响区域示意图。
The assumption of a thin crust leads to a modification of the exponent in Hertz’s expression relating force and penetration, which goes as $F\propto h^{\frac{3}{2}}$ and applies to homogenous spheres. In order to understand the reason for the change, it might be worthwhile to first outline an argument-originally advanced by de Gennes- explaining the usual $\frac{3}{2}$ exponent.
Consistent with the notation of Figure 25, $h$ is the depth of penetration during a collision, and $R$ is the radius of each sphere. From elementary geometry, we can easily derive an expression for the radius $a$ of the contact circle. Assuming that $h$ is very much smaller than $R$, which is justified if we insist on remaining within the elastic regime, the result is $a^{2}\approx Rh$.
薄壳假设导致 Hertz 力与压缩力表达式中的指数发生了变化,变为 $F\propto h^{\frac{3}{2}}$,并适用于均匀球体。为了理解这一变化的原因,不妨先概述一下最初由 de Gennes 提出的一个论点,解释通常的 $\frac{3}{2}$ 指数。
与图 25 的符号一致,$h$ 是碰撞时的压缩深度,$R$ 是每个球体的半径。根据基本几何原理,我们可以很容易地推导出接触圆半径 $a$ 的表达式。假定 $h$ 远远小于 $R$(如果我们坚持在弹性范围内,这是合理的),结果就是 $a^{2}\approx Rh$。
It is not unreasonable to assume that the deformation of colliding spheres affects a depth roughly equal to the radius a of the contact circle. Under these conditions, and in the presence of a stress $P$, the classical definition of Young’s modulus gives a relation of the type
$$ P \approx E\frac{h}{a}. $$
Rearranging terms and combining equations leads to
$$ F\approx Pa^{2} \approx Eha \approx E\sqrt{R}h^{\frac{3}{2}}. $$
假设碰撞球体的变形影响深度大致等于接触圆的半径 a 并非不合理。在这些条件下,并在存在应力 $P$ 的情况下,杨氏模量的经典定义给出了以下关系式
$$ P \approx E\frac{h}{a}. $$
重排项并合并等式,得出
$$ F\approx Pa^{2} \approx Eha \approx E\sqrt{R}h^{\frac{3}{2}}. $$
This justifies the $\frac{3}{2}$ power law. If we now consider a sphere covered with a soft crust of thickness $e$ much smaller than the radius $R$ of the sphere, but sufficiently large compared to the penetration depth $h$, we can assume that the deformation will be localized within the outer layer whose Young’s modulus is $E_{e} \ll E$. In that case, the depth affected will be of the order of $e$, rather than $a$ as in the previous case. In other words, a stress $P$ acting on the sphere now produces a penetration depth given by
$$ P\approx E_{e}\frac{h}{e}. $$
The same algebraic manipulation as before now yields
$$ F\approx Pa^{2} \approx E_{e}\frac{h}{e}a^{2} \approx E_{e}\frac{R}{e}h^{2}. $$
The relation between penetration depth and force has changed from $h\propto F^{2/3}$, valid in the case of Hertz’s homogeneous spheres, to $h\propto F^{1/2}$. The deformation increases more slowly with applied force. This makes sense if we note that, in the presence of a soft crust, the deformation is more localized to regions near the contact point and does not spread as deeply into the core.
这就证明 $\frac{3}{2}$ 幂律是正确的。如果我们现在考虑一个被软壳覆盖的球体,软壳的厚度 $e$ 远远小于球体的半径 $R$,但与穿透深度 $h$ 相比足够大,我们可以假设变形将集中在外层,其杨氏模量为 $E_{e} \ll E$。在这种情况下,受影响的深度将为 $e$,而不是前一种情况中的 $a$。换句话说,作用在球体上的应力 $P$ 现在产生的穿透深度为
$$ P\approx E_{e}\frac{h}{e}. $$
与之前的代数运算相同,现在可以得出
$$ F\approx Pa^{2} \approx E_{e}\frac{h}{e}a^{2} \approx E_{e}\frac{R}{e}h^{2}. $$
挤压深度与力之间的关系从 Hertz 均匀球体情况下的 $h\propto F^{2/3}$ 变为 $h\propto F^{1/2}$。变形随外力增加的速度变慢。如果我们注意到,在存在软地壳的情况下,形变更多地集中在接触点附近的区域,而不会向地核深处扩散,这就说得通了。
Such a dependence can explain, at least in part, certain experimental observations that deviate notably from what would be expected on the basis of Hertz’s model. This is not the only possible explanation. Others have been proposed, invoking notions of disorder and enrichment in the vicinity of contact points under the influence of stress. We shall discuss a particular example in Section 3.1.2.
这种依赖性至少可以部分解释某些实验观察结果与根据 Hertz 模型所预期的结果之间的明显偏差。这并不是唯一可能的解释。人们还提出了其他一些解释,如在应力作用下接触点附近的无序和富集概念。我们将在第 3.1.2 节中讨论一个特殊的例子。
2.3 A Single Particle on Top of a Granular Medium
A sphere rolling down a rough surface looses kinetic energy by friction and successive collisions. Its trajectory is a mix of ballistic arcs and sections of curves following the rough surface.
一个球体在粗糙表面上滚动,由于摩擦和连续碰撞而失去动能。它的运动轨迹是弹道弧线和沿着粗糙表面的曲线段的混合体。
Thus far, we have considered the elementary problem-albeit difficult enough as it is-of the interaction of two particles only. We eventually need to address more general granular materials composed of many indistinguishable particles. To that end, we will introduce laws that are often derived from the mechanics of continuous media, just as the kinetic theory of liquids is a stepping stone to the Navier-Stokes law. In the meantime, we continue down the logical progression of our discussion by considering the case of a single mobile particle interacting with a granular medium assumed to be rigid.
到目前为止,我们只考虑了两个粒子相互作用的基本问题,尽管这个问题已经足够困难。我们最终需要解决, 由许多全同粒子组成的, 更一般性的颗粒材料的问题。为此,我们将引入通常推导自连续介质力学的定律,正如液体动力学理论是通向 Navier-Stokes 定律的垫脚石一样。与此同时,我们将继续按照逻辑顺序进行讨论,考虑单个移动粒子与假定为刚性的颗粒介质相互作用的情况。
As schematically indicated in Figure 26, we can expect such a particle falling down a bumpy slope, whose protrusions are roughly the same size as the particle itself, to follow an irregular and complex path depending on whether it remains in contact with or bounces off its support. We can even predict that this path, made of sections of parabolas (ballistic trajectories) and sections of curves following the contour of the support, will depend strongly on the mechanical characteristics (coefficients of restitution and of friction) of the materials in contact. We can further predict that the path will depend in some complex fashion on the speed of the particle. Under such conditions, is there any prospect of ever writing a global equation describing, even approximately, all these possible behaviors?
如图 26 所示,我们可以预料,从一个凹凸不平的斜坡(斜坡上的突起与颗粒本身的尺度相当)上掉落下来的颗粒会沿着一条不规则的复杂轨迹前进,这取决于它是与支撑物保持接触还是从支撑物上弹起。我们甚至可以预言,这条由抛物线(弹道轨迹)和沿支撑物轮廓的曲线组成的路径,将在很大程度上取决于接触材料的机械特性(恢复系数和摩擦系数)。我们还可以进一步预测,运动轨迹将以某种复杂的方式取决于粒子的速度。在这种情况下,是否有可能写出一个描述(哪怕是近似地描述)所有这些可能行为的全局方程呢?
As a starting point, it is useful to review Newton’s law, which describes the fall of a particle of mass $m$ and diameter $D$ down an inclined slope making an angle $\theta$ with the horizontal plane. The particle interacts with its environment through the bias of a drag force $F$ somewhat analogous to a friction. At this point, we may introduce a normalized acceleration $\Gamma$, a notion we will resort to frequently in what follows. It is a dimensionless number equal to $A/g$, where $A$ is the actual acceleration experienced by the particle and $g$ is the acceleration due to gravity. Newton’s law can thus be written as
$$ \Gamma = \sin{\theta} - \frac{F}{mg}. $$
牛顿定律描述了质量为 $m$、直径为 $D$ 的质点沿着与水平面成 $\theta$ 角的斜坡下落的过程。质点通过阻力 $F$ 的偏向与其环境相互作用,这有点类似于摩擦力。此时,我们可以引入一个归一化加速度 $\Gamma$,在下文中我们将经常使用这个概念。它是一个无量纲的数字,等于 $A/g$,其中 $A$ 是质点经历的实际加速度,$g$ 是重力加速度。因此,牛顿定律可以写成
$$ \Gamma = \sin{\theta} - \frac{F}{mg}. $$
A uniform motion results whenever $\Gamma = 0$, i.e., when the friction force exactly offsets the effect of gravity. It then becomes evident that the problem boils down to working out a plausible expression for the force of friction $F$, as we will see in several examples later in this book (for instance, in Section 4.2.2).
The idealized case described above helps us to understand that the force of friction corresponds to a loss of energy as the particle proceeds down the slope. This allows us to write $F = \partial E/\partial x$, where $x$ corresponds to the distance covered. The energy of the particle of mass $m$ has two components:
- its kinetic energy $E_{k}$ which is dissipated over a characteristic distance $\lambda$ as a result of successive collisions and friction with the support;
- its potential energy $E_{p}$, which also decreases as the particle drops down into a succession of wells of typical depth $D$.
只要 $\Gamma = 0$,即摩擦力完全抵消重力作用时,就会产生匀速运动。这样一来,问题显然就可以归结为给摩擦力 $F$ 计算出一个合理的表达式,我们将在本书后面的几个例子中看到这一点(例如,第 4.2.2 节)。
上述理想化的情况有助于我们理解,摩擦力相当于质点沿斜坡下滑时的能量损失。因此,我们可以写成 $F = \partial E/\partial x$,其中 $x$ 相当于所走的距离。质量为 $m$ 的粒子的能量由两部分组成:
-
其动能 $E_{k}$,由于与支撑物的连续碰撞和摩擦,动能在一个特征距离 $\lambda$ 上耗散;
-
其势能 $E_{p}$,也会随着粒子下降到典型深度 $D$ 的连续井中而减小。
Thus we may write
$$ E_{k} = \frac{1}{2}mv^{2} $$
and
$$ E_{p} = mgh\cos{\theta} $$
where $h$ is the altitude of the particle.
因此,我们可以写出
$$ E_{k} = \frac{1}{2}mv^{2} $$
和
$$ E_{p} = mgh\cos{\theta} $$
其中 $h$ 是粒子的高度。
If we consider that the loss of kinetic energy occurs over a characteristic length $\lambda$ (of the order of a few diameters $D$), we obtain the first component of the friction force $F_{k} = mv^{2}/2\lambda$. In order to derive a suitable expression for the second component $F_{p}$ , corresponding to the loss of potential energy, we use the following argument:
- At high velocity, the freely moving particle executes ballistic flights whose typical range is of the order of $D$. This range can be estimated independently by considering ballistic flights of height $\Delta h\approx (\frac{1}{2}gT^{2})$, where $T$ is the typical time of free flight of a particle moving at speed $v$. In this approximation, the quantity $vT$ corresponds to a typical distance of the order of $D$. Under these conditions, we have $T\approx D/v$, and the force of friction equivalent to the loss of potential energy can be written as
$$ F_{p} = \frac{mg\Delta h}{D} \approx \frac{1}{2}mg\frac{D}{v^{2}}. $$
The equation just derived suggests that the corresponding dissipative force becomes less and less effective as the speed of the particle increases, which certainly conforms to our intuition.
- At low velocity, the path of the particle follows the profile of the surface of the granular support. The resulting loss of potential energy should no longer depend on speed. It corresponds only to the dry friction experienced by the particle as it moves down the surface. In this case we have
$$ F_{p} = mg $$
- At intermediate velocity, we simply interpolate between the two extremes with an equation of the form
$$ F_{p} \approx mg\frac{1}{1 + \beta(v^{2}/gD)}, $$
where $\beta$ is treated as an adjustable parameter. This heuristic expression converges toward the proper limits when $v\rightarrow 0$ or $v\rightarrow\infty$.
如果我们认为动能损失量进行于一个特征长度 $\lambda$ (相当于几个直径 $D$)上,我们就可以得到摩擦力的第一个分量 $F_{k} = mv^{2}/2\lambda$ 。为了推导出与势能损失相对应的第二分量 $F_{p}$ 的合适表达式,我们使用了以下论证:
- 在高速运动时,自由移动的粒子会进行弹道飞行,其典型范围为 $D$。这个范围可以通过考虑高度为 $\Delta h\approx (\frac{1}{2}gT^{2})$ 的弹道飞行来独立估算,其中 $T$ 是以速度 $v$ 运动的粒子的典型自由飞行时间。在这个近似值中,$vT$ 相当于 $D$ 数量级的典型距离。在这些条件下,我们有 $T\approx D/v$,相当于势能损失的摩擦力可写成
$$ F_{p} = \frac{mg\Delta h}{D} \approx \frac{1}{2}mg\frac{D}{v^{2}}. $$
刚才推导出的等式表明,随着粒子速度的增加,相应的耗散力会变得越来越小,这当然符合我们的直觉。
- 在低速情况下,粒子的运动轨迹与颗粒支撑物表面的轮廓完全一致。由此产生的势能损失不再取决于速度。它只与颗粒沿表面向下运动时所经历的干摩擦力相对应。在这种情况下,我们有
$$ F_{p} = mg $$
- 在中间速度下,我们只需在两个极端之间进行插值,方程的形式为
$$ F_{p} \approx mg\frac{1}{1 + \beta(v^{2}/gD)}, $$
其中,$\beta$ 被视为可调参数。当 $v\rightarrow 0$ 或 $v\rightarrow\infty$ 时,这个经验表达式会向正确的极限收敛。
In a final step, we gather both components together in a single expression of the form
$$ F = F_{p} + F_{c} = mg\left[\frac{a}{1 + b(v^{2}/gD)} + c\left(\frac{v^{2}}{gD}\right)\right], $$
where $a$, $b$, and $c$ are dimensionless constants.
最后,我们将这两个部分合并为一个表达式,其形式为
$$ F = F_{p} + F_{c} = mg\left[\frac{a}{1 + b(v^{2}/gD)} + c\left(\frac{v^{2}}{gD}\right)\right], $$
其中,$a$、$b$ 和 $c$ 为无量纲常数。
It is instructive to consider the implications of this very simple model. Figure 16 illustrates the trend of the drag force described by (2-16), with the parameters set to $a = b = 1$ and $c = 0.25$. One interesting feature of our elementary model is that friction does not vanish when $v = O$. Even though the system is then at rest, it still experiences an external stimulus since the curvature of the graph points downward. The particle is in unstable equilibrium; it will start moving when it finds itself on a slope exceeding what is called the angle of movement $\theta_{m}$, in which case the friction force is precisely equal to $mg\cos{\theta_{m}}$.
考虑一下这个非常简单的模型的意义是很有启发的。图 16 显示了设定参数为 $a = b = 1$ 和 $c = 0.25$ 时 (2-16) 所描述的阻力趋势。我们的基本模型有一个有趣的特点,即当 $v = O$ 时,摩擦力并没有消失。尽管此时系统处于静止状态,但由于图形的曲率指向下方(凸函数的极值点),因此仍可能受到外部刺激。粒子处于不稳定平衡状态;当它发现自己所处的斜坡超过了所谓的运动角度 $\theta_{m}$,它就会开始运动,在这种情况下,摩擦力恰好等于 $mg\cos{\theta_{m}}$。

The friction subsequently decreases as the velocity increases, and reaches a minimum value $mg\sin{\theta_{r}}$. The angle $\theta_{r}$ corresponds to a stable equilibrium since the curvature of the graph now points upward. It is called the angle of repose. The corresponding velocity is equal to $\sqrt{gD}$. To the right of that point, the effective friction force increases rapidly, which tends to bring the operating point back down toward the minimum. To a first approximation, the system is constrained to evolving between $\theta_{m}$ and $\theta_{r}$ only.
摩擦力随后随着速度的增加而减小,并达到最小值 $mg\sin{\theta_{r}}$。这个角度 $\theta_{r}$ 相当于一个稳定的平衡点,因为图形的曲率现在指向上方。它被称为休止角。相应的速度等于 $\sqrt{gD}$。在该点的右侧,有效摩擦力迅速增加,从而使运行点向最小值回落。作为一级近似,系统受限于在 $\theta_{m}$ 和 $\theta_{r}$ 之间演化。
We will have an opportunity to make use of all these concepts again when we study avalanches in Chapter 4. But this is a good place to emphasize how simple considerations of exchange of kinetic energy dissipated by friction and potential energy give rise to two equilibrium states, one of which is stable and the other only marginally so. This turns out to be a general characteristic of granular flows.
在第 4 章研究雪崩时,我们将有机会再次使用所有这些概念。不过,这里可以强调一下,简单地考虑摩擦耗散的动能和势能的交换会产生两种平衡状态,其中一种是稳定的,而另一种只是略微稳定。这就是颗粒流动的一般特征。
We may also point out a connection with the stick-slip phenomenon discussed in Section 2.2.1. As we have seen, when the velocity is zero, the system is kept in a stationary state-although in unstable equilibrium-determined by dry friction (coefficient $\mu_{s}$). Under appropriate conditions, it will evolve toward a state of finite speed so as to minimize friction (coefficient $\mu_{d}< \mu_{s}$). Pushing this analogy further, we can anticipate that a real system will tend to oscillate between these two states when subjected to an external stimulus, as will indeed be confirmed in our analysis of avalanches.
Likewise, we may also predict the existence of interesting hysteresis effects associated with the fact that a particle will evolve in different ways depending on the initial conditions. If it starts with a finite speed, it is likely to settle in a state corresponding to the minimum shown in Figure 27. If, on the other hand, it is initially at rest, dry friction will tend to keep it in that state.
我们还可以指出这与第 2.2.1 节讨论的粘滑现象之间的联系。正如我们所看到的,当速度为零时,系统保持静止状态–尽管是不稳定平衡–由干燥摩擦力(系数 $\mu_{s}$)决定。在适当的条件下,它将向有限大小速度的状态演化,从而使摩擦最小化(系数 $\mu_{d}< \mu_{s}$)。进一步类推,我们可以预见,当受到外部刺激时,实际系统会倾向于在这两种状态之间来回切换,这在我们对雪崩的分析中证明。
同样,我们还可以预测存在有趣的延迟效应,即粒子会根据初始条件以不同的方式演变。如果粒子开始时的速度有限,那么它很可能会停留在图 27 所示的最小值状态。另一方面,如果粒子最初处于静止状态,干燥摩擦力会使其继续维持这种状态。
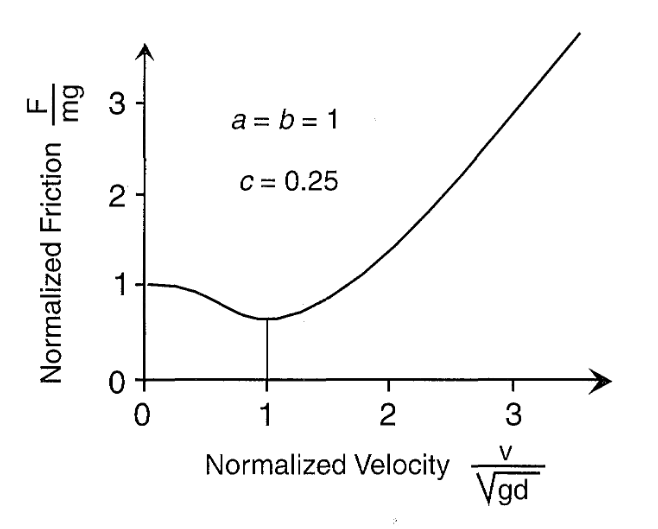
Effective friction force $F$ as a function of the particle’s velocity. The curve does not go through the origin and exhibits a minimum.
有效摩擦力 F$ 与粒子速度的函数关系。曲线并不经过原点,且显现出一个最小值。
More extensive studies of the fall of a sphere down an inclined plane lined with similar fixed spheres have recently be published by several research groups. They attacked the problem either experimentally or through numerical simulations. The reader is urged to consult these references for more details.
最近,一些研究小组发表了关于球体从倾斜平面上坠落的更广泛研究。他们通过实验或数值模拟解决了这一问题。更多详情,请读者参阅这些参考文献。
2.4 Interactions Between Several Particles
2.4.1 The Laws ofFriction in a Granular Medium
Having mastered the laws of friction between solids reviewed earlier in this chapter, we are now in a position to explore how a real granular material reacts to the kind of shearing force involved in Leonardo da Vinci’s experiments. The experimental device illustrated in Figure 28 was originally devised and used by Dawes.
在掌握了本章前面复习的固体间摩擦定律之后,我们现在就可以探索真实的颗粒材料是如何对 Leonardo da Vinci 实验中涉及的那种剪切力做出反应的。图 28 所示的实验装置最初是由 Dawes 设计和使用的。
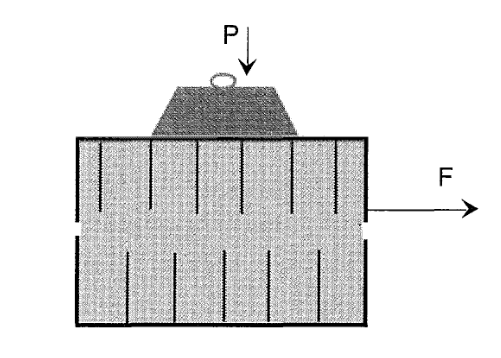
Typical experimental setup used to measure the coefficient of the static friction $\mu_{s}$ of a granular material.
用于测量颗粒材料静摩擦系数 $\mu_{s}$ 的典型实验装置。
It consists of two open boxes with individual compartments shaped like a comb. The two boxes are filled with a granular medium (such as a powder or river sand) and placed upside down on top of each other. A lateral shearing force $F$ is applied to the upper box, which is also subjected to a vertical load $P$.
它由两个打开的盒子组成,每个盒子的隔间形状像梳子。两个盒子中装满颗粒介质(如粉末或河沙),并相互倒置。在上层盒子上施加横向剪切力 $F$,同时承受垂直荷载 $P$。
Without going into the details of the experiments, we state the following experimental observations:
- The shearing force required to set the upper half in lateral motion is strictly proportional to the load $P$ and is independent of the surface area under shear
$$ F = \mu_{s}P. $$
This result is entirely consistent with the first law of solid friction reviewed in Section 2.2.1.
- The coefficient $\mu_{s}$ is of the order of 0.7, which is quite comparable to values typically encountered in the case of friction between solids. The angle $\theta$, given by the formula $\theta=\tan^{-1}{\mu_{s}}$, is approximately equal to $35^{\circ}$. It is useful to keep this value in mind, as it will resurface in Chapter 4.
我们在此不对实验细节进行赘述,只陈述以下实验观察结果:
- 使上半部横向运动所需的剪切力与载荷 $P$ 严格成正比,与受剪切的表面积无关:
$$ F = \mu_{s}P. $$
这一结果完全符合第 2.2.1 节所述的固体摩擦第一定律。
- 系数 $\mu_{s}$ 约为 0.7,与固体间摩擦的典型值相当。角度 $\theta$ 由公式 $\theta=\tan^{-1}{\mu_{s}}$ 得出,大约等于 $35^{\circ}$。记住这个值是很有用的,因为它将在第 4 章中再次出现。
We note in passing that these results hold equally well for cohesive and noncohesive granular materials (cohesive materials are made of particles kept together by cohesive forces). The only difference is that in the cohesive case the above expression must be modified by the addition of a constant term $C$; the expression then takes on the form $F = \mu_{s} P + C$.
我们顺便指出,这些结果同样适用于粘性和非粘性颗粒材料(粘性材料由受内聚力作用而保持在一起的颗粒组成)。唯一不同的是,在有内聚力的情况下,必须通过添加常数项 $C$ 来修改上述表达式; 此时表达式为 $F = \mu_{s} P + C$。
These results have actually been long accepted by people working in the field of soil mechanics, who routinely make use of the concept of stress. Nevertheless, these properties constitute a rather stunning discovery. No one could have predicted them, given the complexity of granular piles and the many unknowns concerning their equilibrium (see Section 3.3.1).
实际上,这些结论早已被土壤力学领域的工作人员所接受,他们经常使用应力的概念。然而,这些特性是一个相当惊人的发现。考虑到颗粒堆的复杂性及其平衡方面的许多未知因素(见第 3.3.1 节),没有人能够预测到这些特性。
In particular, it seems quite unlikely that a model based on plastic deformations, such as we invoked in our discussion of the laws of friction between solids, could be extrapolated to the present situation. The best we can do at this point is to accept that a medium as complex and heterogeneous as a granular can lead to exceedingly simple macroscopic laws. As an aside, the same can be said of two sheets of cardboard in contact.
特别是,我们在讨论固体之间的摩擦定律时所引用的基于塑性变形的模型,似乎不太可能推广到目前的情况。目前,我们所能做的就是接受这样一种事实,即像颗粒这样复杂和异质的介质可以产生极其简单的宏观定律。另外,两张纸板接触时的情况也是如此。
2.4.2 Bagnold’s Number
We now proceed to consider the dynamics of a flowing sheet of granules at most a few particles deep. When a container filled with such a material is tilted beyond a certain angle, the resulting flow normally involves only a limited number of upper layers, say, from 6 to 10. An analysis of this situation, fairly similar to the one we will outline, was carried out by Bagnold. It led to a parameter characterizing the flow of granular materials, which is reminiscent of the familiar Reynold’s number in hydrodynamics.
现在,我们开始考虑最深只有几个颗粒的颗粒流动层的动力学。当装满这种材料的容器倾斜超过一定角度时,所产生的流动通常只涉及有限数量的上层,例如 6 到 10 层。Bagnold 对这种情况进行了分析,与我们将概述的情况相当类似。分析得出了一个表征颗粒材料流动的参数,它让人联想到我们熟悉的流体力学中的 Reynold 数。
Consider a cylindrical container filled with a granular suspension, i.e., a collection of granules in a viscous liquid. A second smaller cylinder, concentric with the first, and dotted with large protuberances, is rotated inside the first. We are interested in the resulting flow pattern of the particles. The following discussion also applies to an “avalanche” flow, obtained for instance by tilting a table covered with a thick layer of granules, as illustrated in Figure 29.
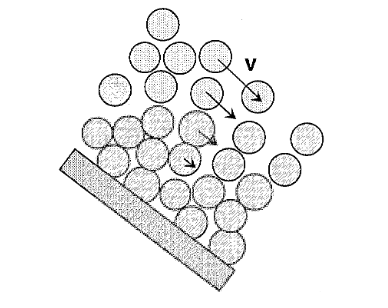
The flow of a granular material medium normally involves only a few layers near the free surface. The mean velocity of the particles decreases rapidly with depth.
颗粒材料介质的流动通常只涉及自由表面附近的几个层。颗粒的平均速度随着深度的增加而迅速减小。
考虑一个装满颗粒悬浮液的圆柱形容器,即粘稠液体中的颗粒聚合体。第二个较小的圆柱体在第一个圆柱体内旋转,与第一个圆柱体同心,上面点缀着大突起。我们感兴趣的是由此产生的颗粒流动模式。下面的讨论也适用于 “雪崩” 流,例如通过倾斜覆盖着厚厚一层颗粒的桌子得到的 “雪崩” 流,如图 29 所示。
Experiments show that any flow takes place in sheets. The movement of the granular material occurs in stratified layers parallel to each other, each layer being characterized by its own velocity, different from that of the adjacent layers. The medium can be viewed as a succession of layers slowed down by friction with layers on either side.
We can introduce a parameter called the rate of shearing of a sheet of granular material in motion on top of another sheet moving at a different velocity. This parameter is a measure of the average velocity gradient and is defined by $\gamma = \langle\partial v/\partial z\rangle$, where $z$ is the depth.
实验表明,任何流动都是片状的。颗粒材料的运动是在相互平行的分层中进行的,每一层都有自己的速度,与相邻层的速度不同。介质可以看作是一个连续的层,由于与两侧层的摩擦而减慢了速度。
我们可以引入一个参数,称为在以不同速度运动的另一个薄片上运动的颗粒材料薄片的剪切率。这个参数是平均速度梯度的量度,定义为:$\gamma = \langle\partial v/\partial z\rangle$ ,其中 $z$ 是深度。
It is evident that the rate of shearing must figure prominently in constructing our model, particularly to account for the loss of kinetic energy by friction. Let $D$ be the diameter of individual particles of mass $m$. The quantity $D\gamma$ measures the relative velocity of this particle with respect to the underlying sheet. The excess loss of kinetic energy, which occurs over a characteristic length $\lambda_{e}$ typically of the order of a few diameters $D$, is due to the friction force $F_{c}$. This we may write
$$ F_{c} = \left\langle\frac{\partial E_{c}}{\partial x}\right\rangle \approx \frac{mD^{2}}{2\lambda_{e}}\gamma^{2}. $$
显然,在构建我们的模型时,剪切速率必须占据重要地位,特别是要考虑到摩擦造成的动能损失。假设 $D$ 是质量为 $m$ 的单个粒子的直径。$D\gamma$ 量评估了该粒子相对于底层薄片的相对速度。动能的过量损失是由于摩擦力 $F_{c}$,它发生在一个特征长度 $\lambda_{e}$ 上,通常为几个直径 $D$ 的数量级。我们可以写成
$$ F_{c} = \left\langle\frac{\partial E_{c}}{\partial x}\right\rangle \approx \frac{mD^{2}}{2\lambda_{e}}\gamma^{2}. $$
We also note that the quantity $\eta\gamma$, where $\eta$ is the viscosity of the interstitial fluid, represents the friction force $F_{v}$ due to viscous interaction with the fluid, divided by the cross-sectional area of the solid in motion, which is of the order of $D^{2}$:
$$ F_{v} = \frac{\eta\gamma}{D^{2}}. $$
Bagnold introduced a number B defined as the ratio of the forces due to friction and collisions between solids to the forces exerted by the viscous fluid. 13 In other words
$$ B = \frac{F_{c}}{F_{v}} \approx \frac{m\gamma}{2\lambda_{e}\eta}. $$
Two distinct regimes can be defined depending on the relative importance of $F_{c}$ and $F_{v}$ . In particular:
$B < 40$ corresponds to a regime known as macro-viscous, in which energy is dissipated primarily by way of viscous interaction with the ambient fluid. Physically, the fluid does most of the work to set the particles in motion. Only rarely do the particles come in contact with each other. Actual examples of macro-viscous systems include muds, moist pastes, and solid particles in suspension.
$B > 450$ corresponds to an essentially granular regime, in which most of the energy is dissipated by collisions and friction between the solid particles.
The intermediate case requires some caution.
3 Fluidization, Decompaction, and Fragmentation
Common sense tells us that, in the absence of any external perturbation, a pile of granular material is at rest. It can be inclined, gently shaken, and submitted to various mild stimuli without anything drastic happening, in other words without triggering a flow or collapse, and without affecting the relative positions of the granules. We also know from experience that a sufficiently high inclination can set off an avalanche, possibly even a continuous or intermittent flow; that vibrations cause a granular material to behave somewhat like a liquid; and that sand deforms readily when crushed. All these properties are markedly different from those of the normal solids, liquids, and gases we are accustomed to. The main difference appears to be that granular materials must be “sufficiently” perturbed in order to change. This observation strongly suggests that we will be dealing with issues such as thresholds, nonlinearities, and hysteresis effects.


