Adrian Baule, Flaviano Morone, Hans J. Herrmann, Hernán A. Makse.

Abstract

In 1989, Sir Sam Edwards made the visionary proposition to treat jammed granular materials using a volume ensemble of equiprobable jammed states in analogy to thermal equilibrium statistical mechanics, despite their inherent athermal features. Since then, the statistical mechanics approach for jammed matter—one of the very few generalizations of Gibbs-Boltzmann statistical mechanics to out-of-equilibrium matter—has garnered an extraordinary amount of attention by both theorists and experimentalists. Its importance stems from the fact that jammed states of matter are ubiquitous in nature appearing in a broad range of granular and soft materials such as colloids, emulsions, glasses, and biomatter.

1989 年，Sam Edwards 爵士提出了一个具有远见卓识的建议，即尽管颗粒材料本身具有热平衡统计力学的特征，但仍应类比热平衡统计力学，使用可等价堵塞态的体积系综来处理堵塞颗粒材料。从那时起，堵塞态物质的统计力学方法– Gibbs-Boltzmann 统计力学对非平衡物质的极少数概括–就受到了理论家和实验家的极大关注。它的重要性源于这样一个事实：物质的堵塞态在自然界中无处不在，出现在胶体、乳液、玻璃和生物物质等各种颗粒状和软性材料中。

Indeed, despite being one of the simplest states of matter—primarily governed by the steric interactions between the constitutive particles—a theoretical understanding based on first principles has proved exceedingly challenging.

Here a systematic approach to jammed matter based on the Edwards statistical mechanical ensemble is reviewed. The construction of microcanonical and canonical ensembles based on the volume function, which replaces the Hamiltonian in jammed systems, is discussed. The importance of approximation schemes at various levels is emphasized leading to quantitative predictions for ensemble averaged quantities such as packing fractions and contact force distributions.

事实上，尽管堵塞态物质是一种最简单的物质状态–主要由构成粒子之间的立体相互作用所支配–但基于第一性原理的理论理解却极具挑战性。

本文回顾了基于 Edwards 统计力学系综的堵塞物质系统方法。讨论了基于体积函数的微正则系综和正则系综的构建，体积函数取代了堵塞系统中的哈密顿。文章强调了各级近似方案的重要性，从而对堆积分数和接触力分布等系综平均量进行了定量预测。

An overview of the phenomenology of jammed states and experiments, simulations, and theoretical models scrutinizing the strong assumptions underlying Edwards approach is given including recent results suggesting the validity of Edwards ergodic hypothesis for jammed states. A theoretical framework for packings whose constitutive particles range from spherical to nonspherical shapes such as dimers, polymers, ellipsoids, spherocylinders or tetrahedra, hard and soft, frictional, frictionless and adhesive, monodisperse, and polydisperse particles in any dimensions is discussed providing insight into a unifying phase diagram for all jammed matter.

本书概述了堵塞态的现象学，并通过实验、模拟和理论模型对 Edwards 方法的基本假设进行了仔细研究，包括最近的研究结果，这些结果表明 Edwards 堵塞状态的遍历假说是正确的。讨论了构成粒子从球形到非球形（如二聚体、聚合体、椭球体、球面体或四面体）、硬粒子和软粒子、摩擦粒子、无摩擦粒子和粘合粒子、单分散粒子和多分散粒子等任何维度的堆积的理论框架，为所有堵塞物质的统一相图提供了见解。

Furthermore, the connection between the Edwards ensemble of metastable jammed states and metastability in spin glasses is established. This highlights the fact that the packing problem can be understood as a constraint satisfaction problem for excluded volume and force and torque balance leading to a unifying framework between the Edwards ensemble of equiprobable jammed states and out-of-equilibrium spin glasses.

此外，我们还建立了自旋玻璃中亚稳态堵塞的 Edwards 系综与亚稳态之间的联系。这凸显了这样一个事实，即堆积问题可以理解为排除体积和力与力矩平衡的约束满足问题，从而在 Edwards 可等价堵塞态系综与非平衡态自旋玻璃之间建立了一个统一的框架。

INTRODUCTION

Materials composed of macroscopic grains such as sand, sugar, and ball bearings are ubiquitous in our everyday experience. Nevertheless, a fundamental description of both static and dynamic properties of granular matter has proven exceedingly challenging. Take, for example, the pouring of sand into a sandpile; see Fig. 1(a). This process can be considered as a simple example of a fluid-to-solid phase transition of a multiparticle system.

在我们的日常生活中，由沙子、糖和滚珠轴承等宏观颗粒组成的材料无处不在。然而，要从根本上描述颗粒物质的静态和动态特性，已被证明具有极大的挑战性。以将沙子倒入沙堆为例；见图 1(a)。这个过程可以看作是多粒子系统从流体到固体相变的一个简单例子。

However, it is not clear whether this transition is governed by a variational principle of an associated thermodynamic quantity such as the free energy in equilibrium systems. Granular materials do not explore different configurations in the absence of external driving because thermal fluctuations induce negligible particle motion at room temperature and intergrain dissipation and friction quickly drain the kinetic energy from the system.

On the other hand, the jammed state of granular matter bears a remarkable resemblance with an amorphous solid: both are able to sustain a nonzero shear stress; the phase transition from liquid to solid states and the analogous jamming transition in grains are both governed by one or a few macroscopic control parameters; and, when using certain packing-generation protocols, macroscopic observables, such as the packing fraction, are largely reproducible.

然而，尚不清楚这种转变是否受相关热力学量（如平衡态系统中的自由能）的变异原理支配。颗粒材料在没有外部驱动的情况下不会探索不同的构型，因为在室温下，热波动引起的颗粒运动可以忽略不计，而颗粒间的耗散和摩擦会迅速耗尽系统的动能。

另一方面，颗粒物质的堵塞状态与无定形固体有着显著的相似之处：两者都能承受非零剪切应力；从液态到固态的相变以及颗粒中类似的堵塞转变都受一个或几个宏观控制参数的制约；而且，在使用某些堆积生成协议时，堆积分数等宏观观测指标在很大程度上是可重复的。

---

Jamming transitions not only occur in granular media, but also in soft materials such as colloidal suspensions which may asymptotically reach jamming under centrifugation, compressed emulsions, foams, glasses, and spin glasses below their glass transition temperature and biological materials such as cells, DNA, and protein packing. Even more broadly, the jamming transition pertains to a larger family of computational problems named constraint satisfaction problems (CSPs) (Krzakala and Kurchan, 2007).

堵塞转变不仅发生在颗粒介质中，也发生在软性材料中，如在离心作用下可能渐进达到堵塞的胶体悬浮液、压缩乳液、泡沫、玻璃和低于玻璃化温度的自旋玻璃，以及生物材料，如细胞、DNA 和蛋白质堆积。更广义地说，堵塞转变涉及到一个更大的计算问题集群，即约束满足问题（CSP）（Krzakala 和 Kurchan，2007 年）

These problems involve finding the values of a set of variables simultaneously satisfying all the constraints imposed on those variables and maximizing (or minimizing) an objective function. For example, in the problem of sphere packings, the goal is to minimize the volume occupied by the packing subject to the geometrical constraint of nonoverlapping particles and the mechanical constraints of force and torque balance at mechanical equilibrium.

这些问题涉及找到一组变量的值，同时满足施加在这些变量上的所有约束条件，并使目标函数最大化（或最小化）。例如，在球体堆积问题中，目标是在颗粒不重叠的几何约束和机械平衡时力和力矩平衡的机械约束下，使堆积所占体积最小。

In general, packing problems play a central role in various fields of science in addition to physics, such as discrete mathematics, number theory, and information theory. An example of practical interest is the problem of efficient data transmission through error-correcting codes, which is deeply related to the optimal packing of (Hamming) spheres in a high-dimensional space (Conway and Sloane, 1999). The common feature of all packing problems is the existence of a phase transition, the jamming transition, separating the phase where the constraints are satisfiable from a phase where they are unsatisfiable.

一般来说，除物理学外，堆积问题在离散数学、数论和信息论等多个科学领域都发挥着核心作用。一个具有实际意义的例子是通过纠错码进行高效数据传输的问题，它与高维空间中（Hamming）球的最优堆积问题有着深刻的联系（Conway 和 Sloane，1999 年）。所有堆积问题的共同特征是存在一个阶段转换，即堵塞态转换，它将约束条件可满足的相与约束条件不可满足的相分开。

---

The existence of constraints in physical systems causes, in general, a significant metastability. Metastability is the phenomenon by which the system remains confined for a relatively long time in suboptimal regions of the phase space. It is related to the rough energy (or free energy) landscape characterized by the presence of many nontrivially related minima as a function of the microscopic configurations (or the macroscopic states). Metastability is, indeed, the leitmotiv in most complex physical systems, whatever its origin.

一般来说，物理系统中制约因素的存在会导致显著的亚稳性。亚稳性是指系统在相空间的次优区域内相对较长时间保持束缚的现象。它与粗糙能（或自由能）绘景有关，其特征是存在许多与微观构型（或宏观状态）函数无关的极小值。事实上，无论其起源如何，亚稳性都是大多数复杂物理系统的主要特征。

For example, in granular materials metastability arises from geometrical and mechanical constraints, but it is found also in spin glasses, which are magnetic systems with competing ferromagnetic and antiferromagnetic exchange interactions.

In spin glasses, the emergence of metastability is due to frustration, which is the inability of the system to simultaneously satisfy all local ordering requirements. Notwithstanding their differences, these two physical systems, jammed grains and spin glasses, exhibit a remarkably similar organization of their metastable states, a fact that stimulates our search for further analogies within these systems and common explanations. It is, indeed, this analog approach, as best exemplified by the encompassing vision of Sir Sam Edwards (Goldbart, Goldenfeld, and Sherrington, 2005), that may shed new light on the solution to jamming problems otherwise doomed to remain obscure.

例如，在颗粒材料中，亚稳性产生于几何和机械约束，但在自旋玻璃中也发现了亚稳性，自旋玻璃是具有竞争性铁磁和反铁磁交换相互作用的磁性系统。

在自旋玻璃中，出现亚稳性的原因是阻挫，即系统无法同时满足所有局部有序要求。尽管存在差异，但这两种物理系统–堵塞颗粒和自旋玻璃–在其亚稳态的组织上表现出了惊人的相似性，这一事实激励了我们在这些系统中寻找进一步的类比和共同的解释。Sam Edwards 爵士（Goldbart、Goldenfeld 和 Sherrington，2005 年）的远见卓识正是这种类比方法的最佳例证，它可能会为解决堵塞问题带来新的曙光，否则这些问题注定会晦涩难懂。

---

Because of their substantial metastability, these systems are fundamentally out of equilibrium even in a macroscopically quiescent state.

Nevertheless, the commonalities with equilibrium many-body systems suggest that ideas from equilibrium statistical mechanics might be useful.

In this review, we consider theories for jammed matter based on generalizations of equilibrium ensembles. These statistical mechanics-based approaches were pioneered by Sir Sam F. Edwards in the late 1980s; see Fig. 1(b).

由于这些系统具有很大的亚稳性，因此即使在宏观静止状态下，它们从根本上也是不平衡的。

尽管如此，与平衡多体系统的共性表明，平衡态统计力学的思想可能是有用的。

在这篇综述中，我们考虑了基于平衡系综广义化的干扰物质理论。这些基于统计力学的方法是萨姆-F-爱德华兹爵士在 20 世纪 80 年代末开创的；见图 1(b)。

---

Investigations of the structural properties of jammed packings are much older. In fact, the related problem of identifying the densest packing of objects has an illustrious history in the mathematical literature (Kepler, 1611; Weaire and Aste, 2008). Exact mathematical proofs of the densest packings are extremely challenging even for spherical particles. The Kepler conjecture of 1611 stating that the densest arrangement of spheres in three spatial dimensions (3D) is a face-centeredcubic (fcc) crystal with a packing volume fraction $\phi_{\text{fcc}} = \pi/(3\sqrt{2})\approx 0.74048\dots$ remained an unsolved mathematical problem for almost four centuries (Kepler, 1611; Hales, 2005).

Systematic experiments on disordered hard-sphere packings began in the 1960s with the work of Bernal (Bernal and Mason, 1960; Bernal, 1964). These experiments are conceptually simple, yet give fundamental insight into the structure of dense liquids, glasses, and jammed systems.

Equally sized spherical particles were placed into a container and compactified by shaking or tapping the system until no further volume reduction was detected. These experiments typically yielded configurations with packing fraction $\phi_{\text{rcp}}\approx 0.64$, which is historically referred to as random close packing (rcp).

对堵塞态堆积物结构特性的研究要早得多。事实上，确定物体最密堆积的相关问题在数学文献中有着辉煌的历史（开普勒，1611 年；Weaire 和 Aste，2008 年）。即使对于球形粒子，最密堆积的精确数学证明也极具挑战性。1611 年的开普勒猜想指出，三维空间（3D）中最致密的球体排列是面心立方（fcc）晶体，其堆积体积分数为 $\phi_{\text{fcc}} = \pi/(3\sqrt{2})\approx 0.74048\dots$ ，这一猜想在近四个世纪中一直是一个未解的数学难题（Kepler, 1611; Hales, 2005）。

关于无序硬球堆积的系统实验始于 20 世纪 60 年代伯纳尔的工作（伯纳尔和梅森，1960 年；伯纳尔，1964 年）。这些实验概念上很简单，但对致密液体、玻璃和堵塞体系的结构提供了根本性的见解。

将大小相等的球形颗粒放入容器中，通过摇晃或敲击系统进行压实，直到检测到体积不再缩小为止。这些实验通常会产生堆积分数约为 $0.64$ 的结构，历史上称之为随机紧密堆积（Random Close Packing, $\text{rcp}$）。

---

In order to apply a statistical mechanical framework to these jammed systems, it is first necessary to identify the variables characterizing the state of the system macroscopically. Clearly, the system energy is not suitable, since it may either not be conserved (for frictional dissipative particles) or not be relevant (for frictionless hard particles). On the other hand, an obvious state variable is the system volume.

In fact, unlike in equilibrium systems, the volume in jammed systems is not an externally imposed fixed variable, but rather depends on the microscopic configuration of the grains. Edwards first extraordinary insight was to parametrize the ensemble of jammed states by the volume function $\mathcal{W}(\{\mathbf{r},\hat{\mathbf{t}}_{i}\})$ ,as a function of the $N$ particles positions $\{\mathbf{r}_{i}\}$ and orientations $\{\hat{\mathbf{t}}_{i}\}$, as a replacement for the Hamiltonian in the equilibrium ensembles (Edwards and Oakeshott, 1989; Mehta and Edwards, 1990; Edwards, 1991, 1994).

为了将统计力学框架应用于这些堵塞态系统，首先需要确定用于表征系统宏观状态的变量。显然，系统能量并不合适，因为它可能不守恒（对于摩擦耗散粒子）或不相关（对于无摩擦硬粒子）。另一方面，一个明显的状态变量是系统体积。

事实上，与平衡系统不同，堵塞态系统中的体积并不是一个外部强加的固定变量，而是取决于颗粒的微观构型。Edwards 的第一个非凡见解是用体积函数 $\mathcal{W}(\{\mathbf{r},\hat{\mathbf{t}}_{i}\})$ 参数化堵塞态的系综、作为 $N$ 粒子位置 $\{\mathbf{r}_{i}\}$ 和方向 $\{\hat{\mathbf{t}}_{i}\}$ 的函数，以替代平衡态系综中的哈密顿量（Edwards 和 Oakeshott, 1989；Mehta and Edwards, 1990; Edwards, 1991, 1994）。

---

A second crucial point in the development of the Edwards granular statistical mechanics is a proper definition of the jammed state. It is important to note that only jammed configurations $\{\mathbf{r}_{i},\hat{\mathbf{t}}_{i}\}$ are included in the ensemble. A definition of what we mean by jammed state is not a trivial task and will be treated rigorously in the next section.

Assuming that an unambiguous definition of metastable jammed state can be expressed analytically, then a statistical mechanics approach to granular matter proceeds by analogy with equilibrium systems.

In this case, the volume function allows for the definition of a granular entropy leading to both microcanonical and canonical formulations of the volume ensembles. This implies, in particular, the existence of an intensive parameter conjugate to the volume. This temperaturelike parameter was called compactivity by Edwards.

Edwards 颗粒统计力学发展过程中的第二个关键点是对堵塞状态的正确定义。重要的是要注意，只有堵塞构型 $\{\mathbf{r}_{i},\hat{\mathbf{t}}_{i}\}$ 才包含在系综中。我们对 “堵塞态” 的定义并非易事，将在下一节进行严格讨论。

假定可以用分析的方法明确定义 亚稳堵塞态，那么颗粒物质的统计力学方法就可以类比于平衡系统。

在这种情况下，通过体积函数可以定义颗粒(系统)版的熵，从而得出体积系综的微正则和正则公式。这尤其意味着存在一个与体积共轭的强度参量。这个类比于温度的参数被 Edwards 称为致密度。

---

The full Edwards ensemble is characterized by the macroscopic volume and, further, by the stress of the packing. Since analytical treatments of the full ensemble are challenging, one typically considers suitable approximations. Neglecting correlations between the volume and the stress leads to a volume ensemble under the condition of isostaticity (Song, Wang, and Makse, 2008).

The core of this review is devoted to elaborate on a mean-field formulation of the Edwards volume ensemble that can potentially lead to a unifying phase diagram encompassing all jammed matter ranging from systems made of spherical to nonspherical particles, with friction or adhesion to frictionless particles, monodisperse and polydisperse systems and in any dimension.

Likewise, we describe frameworks for stress and force statistics alone, such as the stress ensemble (Henkes, O’Hern, and Chakraborty, 2007; Chakraborty, 2010), force network ensemble (Bouchaud, 2002; Snoeijer et al., 2004; Tighe et al., 2010), and belief propagation for force transmission (Bo et al., 2014).

Edwards 全系综的特征是宏观体积和堆积应力。由于全系综的分析处理具有挑战性，人们通常会考虑合适的近似值。忽略体积和应力之间的相关性，可以得到等静压条件下的体积系综（Song、Wang 和 Makse，2008 年）。

这篇综述的核心内容是详细阐述 Edwards 体积系综的平均场公式，它有可能导出一个统一的相图，涵盖从球形粒子到非球形粒子、有摩擦/粘附到无摩擦粒子、单分散和多分散系统以及任何维数空间的所有堵塞物质。

同样，我们还介绍了单独的应力和力统计框架，如应力系综（Henkes、O’Hern 和 Chakraborty，2007 年；Chakraborty，2010 年）、力网络系综（Bouchaud，2002 年；Snoeijer 等人，2004 年；Tighe 等人，2010 年）以及力传递的置信度传播（Bo 等人，2014 年）。

---

Edwards statistical mechanical ensemble relies on two assumptions: (i) ergodicity and (ii) equiprobability of microstates. These assumptions have been scrutinized in the literature, and the questions raised in this context will be reviewed here. Despite these critiques, the Edwards approach was used to describe a wide range of jammed and glassy materials.

Edwards 统计力学系综依赖于两个假设：(i)遍历性和(ii)微观状态的等价性。文献中对这些假设进行了仔细研究，本文将对在此背景下提出的问题进行回顾。尽管存在这些批评意见，爱德华兹方法仍被用于描述较广领域的堵塞和玻璃态材料。

Early works adopted the concept of inherent structures from glasses (Coniglio and Herrmann, 1996; Coniglio and Nicodemi, 2000, 2001; Coniglio, Fierro, and Nicodemi, 2002; Fierro, Nicodemi, and Coniglio, 2002b) and effective temperatures (Kurchan, 2000, 2001; Makse and Kurchan, 2002; Ono et al.,2002; O’Hern, Liu, and Nagel, 2004; Ciamarra, Coniglio, and Nicodemi, 2006; Cugliandolo, 2011) with applications to plasticity (Lieou and Langer, 2012). More recent approaches are based on replica theory for hard-sphere glasses (Parisi and Zamponi, 2010; Charbonneau et al., 2017).

早期研究采用了玻璃内禀结构概念（Coniglio 和 Herrmann，1996 年；Coniglio 和 Nicodemi，2000 年，2001 年；Coniglio、Fierro 和 Nicodemi，2002 年；Fierro、Nicodemi 和 Coniglio，2002 年 b）和有效温度概念（Kurchan，2000 年，2001 年；Makse 和 Kurchan，2002 年；Ono 等人，2002 年O’Hern、Liu 和 Nagel，2004；Ciamarra、Coniglio 和 Nicodemi，2006；Cugliandolo，2011），并应用于塑性（Lieou 和 Langer，2012）。最近的方法是基于硬球玻璃的复制理论（Parisi 和 Zamponi，2010 年；Charbonneau 等人，2017 年）。

Valuable insight is gained from models that exhibit both jamming and glass transitions (Krzakala and Kurchan, 2007; Mari, Krzakala, and Kurchan, 2009; Ikeda, Berthier, and Sollich, 2012). In this review, we emphasize that the Edwards ensemble can be recast as a constraint satisfaction problem, which allows for a unifying view of hard-sphere glasses and spin glasses through a synthesis applied at the foundation of granular statistical mechanics.

我们从同时表现出堵塞态和玻璃化转变的模型中获得了宝贵的见解（Krzakala 和 Kurchan，2007 年；Mari、Krzakala 和 Kurchan，2009 年；Ikeda、Berthier 和 Sollich，2012 年）。在这篇综述中，我们强调 Edwards 系综可被重塑为一个约束求解问题，通过在粒状统计力学基础上应用的综合方法，可以统一硬球玻璃和自旋玻璃的观点。

---

This review is organized as follows.

In Sec. II we discuss the foundations of the ensemble approach via the rigorous definition of metastable jammed states and the construction of microcanonical and canonical ensembles based on the volume function and stress-moment tensor, which play the role of the Hamiltonian in jammed systems.

In Sec. III we collect empirical results on the phenomenology of jammed states. Moreover, we review results from experiments, simulations, and theoretical models that test the ergodic and uniform measure underlying the ensemble approach.

In Sec. IV we consider volume ensembles and their mean-field description, which provides quantitative predictions for ensemble averaged quantities such as the packing fraction of spherical and nonspherical particles.

In Sec. V we discuss a unification between the Edwards ensemble of jammed matter and theories based on ideas from glass and spin-glass theories under the CSP paradigm.

In Sec. VI we finally close with a summary and a collection of open questions for future work.

本综述编排如下。

在第二节中，我们讨论了系综方法的基础，即严格定义的亚稳堵塞态，以及基于体积函数和应力-力矩张量构建微正则和正则系综，它们在堵塞态系统中扮演着哈密顿量的角色。

在第三节中，我们收集了有关堵塞态现象学的经验结果。此外，我们还回顾了实验、模拟和理论模型的结果，这些结果检验了系综方法所依据的遍历和平均计量。

在第四节中，我们考虑了体积系综及其平均场描述，这为系综平均量（如球形和非球形粒子的堆积分数）提供了定量预测。

在第五节中，我们将讨论在 CSP(Constraint Satisfaction Problem) 范式下，爱德华兹干扰物质集合与基于玻璃和自旋玻璃理论思想的理论之间的统一。

在第六节中，我们最后进行了总结，并提出了未来工作的一些开放性问题。

---

In recent years a number of reviews have appeared dealing with more specific aspects of granular matter: Richard et al. (2005) (granular compaction), Makse, Brujić, and Edwards (2005) (jammed emulsions), Chakraborty (2010) and Bi et al. (2015) (stress ensembles), Tighe et al. (2010) (force network ensemble), and Cugliandolo (2011) and Qiong and Mei-Ying (2014) (effective temperatures).

The present review is also complementary to other reviews on jammed granular matter, which do not specifically discuss the Edwards thermodynamics: Jaeger, Nagel, and Behringer (1996), Alexander (1998), Kadanoff (1999), Liu and Nagel (2010), Parisi and Zamponi (2010), Torquato and Stillinger (2010), van Hecke (2010), Borzsonyi and Stannarius (2013), and Charbonneau et al. (2017).

Our work puts these topics into the general context of Edwards statistical mechanics and provides an overview of the immense amount of literature related to Edwards ensemble approaches.

近年来，出现了一些涉及颗粒物质更具体方面的综述：Richard等人（2005年）（颗粒压实）、Makse、Brujić和Edwards（2005年）（堵塞乳状液）、Chakraborty（2010年）和Bi等人（2015年）（应力系综）、Tighe等人（2010年）（力网络系综）以及Cugliandolo（2011年）和Qiong和Mei-Ying（2014年）（有效温度）。

本综述也是对其他未专门讨论 Edwards 热力学的有关堵塞颗粒物质的综述的补充：Jaeger、Nagel 和 Behringer (1996)、Alexander (1998)、Kadanoff (1999)、Liu 和 Nagel (2010)、Parisi 和 Zamponi (2010)、Torquato 和 Stillinger (2010)、van Hecke (2010)、Borzsonyi 和 Stannarius (2013) 以及 Charbonneau 等人 (2017)。

我们的工作将这些主题置于 Edwards 统计力学的大背景下，并概述了与 Edwards 系综方法有关的大量文献。

STATISTICAL MECHANICS FOR JAMMED GRANULAR MATTER

In a jammed system all particle motion is prevented due to the confinement by the neighboring particles. The transition to a jammed state is thus not controlled by the temperature as conventional phase transitions in systems at thermal equilibrium, but by geometrical and mechanical constraints imposed by all particles in the system.

Therefore, jammed states can be regarded as the set of solutions in the general class of CSPs, which we term the jamming satisfaction problem (JSP), where the constraints are fixed by the mechanical stability of the blocked configurations of grains.

From this standpoint, the jamming problem has a wider scope than the pure physical significance, encompassing the broader class of CSPs: the unique feature of the packing problem in the large universe of CSPs is that this system allows for a direct and relatively simple experimental test of theoretical predictions.

在堵塞系统中，由于邻近粒子的约束，所有粒子运动都被限制。因此，向堵塞态的转变不像热平衡系统中的传统相变那样受温度控制，而是受系统中所有粒子施加的几何和机械限制。

因此，堵塞状态可视为一般 CSP（我们称之为堵塞满足问题 (JSP, Jamming Satisfaction Problem)）中的解集，其中的约束条件由堵塞颗粒构型的机械稳定性固定。

从这个角度来看，堵塞问题比纯物理意义上的堵塞问题范围更广，涵盖了更广泛的 CSP 类别; 在 CSP 大范围中，堆积问题的独特之处在于，这个系统可以对理论预测进行直接而相对简单的实验检验。

Definition of jammed states

We consider an assembly of $N$, for simplicity, monodisperse particles described by the configurations of the particles $\{\mathbf{r}_{1},\hat{\mathbf{t}}_{1};\dots;\mathbf{r}_{N},\hat{\mathbf{t}}_{N}\}$, where $\mathbf{r}_{i}$ denotes the $i_{\text{th}}$ particle’s position (of its center of mass) and $\hat{\mathbf{t}}_{i}$ its orientation. The first problem we address concerns the definition of a blocked configuration of the particles, i.e., the jammed states. To be jammed the system has to satisfy both excluded volume and mechanical constraints.

我们考虑一个由 $N$（为简单起见）单分散粒子组成的集合体，该集合体由粒子 $\{\mathbf{r}_{1},\hat{\mathbf{t}}_{1};\dots;\mathbf{r}_{N},\hat{\mathbf{t}}_{N}\}$ 其中 $\mathbf{r}_{i}$ 表示第 $i$ 个粒子的位置（质心），$\hat{\mathbf{t}}_{i}$ 表示其取向。我们要解决的第一个问题是如何定义粒子的受阻构型，即堵塞态。系统必须同时满足排除体积约束和机械约束才能被堵塞住。

The excluded volume constraint enforces the fact that particles do not overlap, and its mathematical implementation depends on the shape of the particles. For a system of monodisperse hard spheres, this constraint takes on the following form:

$$ |\mathbf{r}_{i} - \mathbf{r}_{j}|\geq 2R \quad(\text{equal-size hard spheres}) $$

which means that the centers of any pair of particles $i$ and $j$ must be at a distance twice as large as their radius $R$. The hardcore constraint in Eq. (1) is valid only for monodisperse spheres, but it can be generalized to polydisperse and nonspherical particles.

排除体积约束强制要求粒子不重叠，其数学实现取决于粒子的形状。对于单分散硬球系统，该约束条件的形式如下:

$$ |\mathbf{r}_{i} - \mathbf{r}_{j}|\geq 2R \quad(\text{等体积硬球}) $$

这意味着任何一对(最近邻)粒子 $i$ 和 $j$ 的中心距离必须是它们半径 $R$ 的两倍。公式 (1) 中的硬核约束仅适用于单分散球体，但也可推广到多分散和非球形粒子。

---

The excluded volume constraint is necessary but not sufficient by itself to determine whether a configuration of particles is jammed.

Indeed, it has to be supplemented by a constraint enforcing the mechanical stability of the system, requiring that particles satisfy the force and torque balance conditions.

We denote by $\mathbf{d}^{i}_{a}$ the vector connecting $\mathbf{r}_{i}$ and the $a$ th contact on the $i$ th particle.

At this contact there is a corresponding force vector $\mathbf{f}_{a}^{i}$ on particle $i$ arising from the contacting particle.

排除体积约束是必要的，但它本身并不足以确定粒子构型是否被堵塞。

事实上，它还必须辅以一个强制系统机械稳定性的约束，要求粒子满足力和力矩平衡条件。

我们用 $\mathbf{d}^{i}_{a}$ 表示连接 $\mathbf{r}_{i}$ 和第 $i$ 个粒子上第 $a$ 个接触点的向量。

在这个接触点上，粒子 $i$ 上有一个由接触粒子产生的相应力向量 $\mathbf{f}_{a}^{i}$.

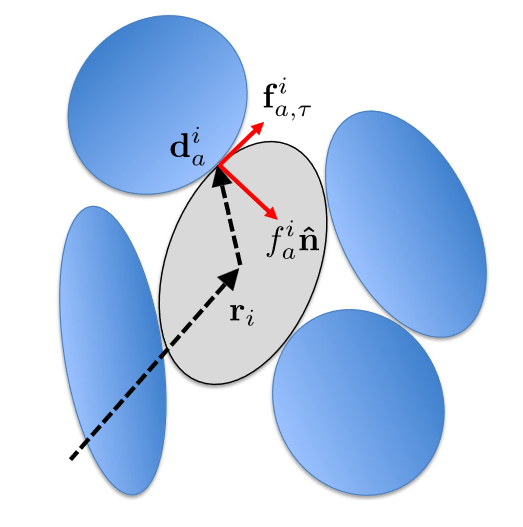
Parametrization of a jammed configuration involving five nonspherical grains. The tangential $\mathbf{f}_{a,\tau}^{i}$ and normal force vectors $f_{a,n}^{i}\hat{n}_{a}^{i}$ at contact $a$ on particle $i$ are shown.

$d_{a}^{i}$ indicates the vector from the center of particle $i$ to the contact point $a$ between one of its neighbors. $r_{i}$ gives the location of the center of particle $i$.

The gray-shaded particle is mechanically stable if all forces and torques generated at the four contact points cancel [see Eqs. (2) and (3)].

涉及五个非球形颗粒堵塞构型的参数化。图中显示了颗粒 $i$ 上接触点 $a$ 处的切向力矢量 $\mathbf{f}_{a,\tau}^{i}$ 和法向力矢量 $f_{a,n}^{i}\hat{n}_{a}^{i}$.

$d_{a}^{i}$表示从粒子 $i$ 的中心到其一个邻居之间的接触点 $a$ 的矢量。$r_{i}$ 表示粒子 $i$ 中心的位置。

如果四个接触点上产生的所有力和力矩相抵消，则灰色阴影部分的质点具有机械稳定性[见公式 (2) 和 (3)]。

With this notation we can formulate the conditions of force and torque balances for a particle of general shape:

$$ \sum_{a\in\partial i}\mathbf{f}_{a}^{i} = 0,\quad i = 1,\dots,N,\\ \sum_{a\in\partial i}\mathbf{d}_{a}^{i}\times\mathbf{f}_{a}^{i},\quad i = 1,\dots, N, $$

where the notation $\partial i$ denotes the set of contacts of particle $i$. Equations (2) and (3) apply to both frictional and frictionless particles. In the latter case there is only one single force component in the normal direction

$$ \mathbf{f}_{a}^{i} = -f_{a}^{i}\hat{\mathbf{n}}_{a}^{i}\quad(\text{frictionless}), $$

where $\hat{\mathbf{n}}_{a}^{i}$ denotes the normal unit vector at the contact point, which depends on the particle shape. For frictional particles, we can decompose $\mathbf{f}_{a}^{i}$ into a normal component $f_{a,n}^{i}$ and a force vector in the tangent plane $f_{a,\tau}^{i}$ (see Fig. 2). Coulomb’s law with friction coefficient $\mu$ is then expressed by the inequality

$$ |f_{a,\tau}^{i}|\leq \mu f_{a,n}^{i}\quad(\text{frictional}). $$

利用这个标记，我们可以为一般形状的质点制定力和力矩平衡的条件：

$$ \sum_{a\in\partial i}\mathbf{f}_{a}^{i} = 0,\quad i = 1,\dots,N,\\ \sum_{a\in\partial i}\mathbf{d}_{a}^{i}\times\mathbf{f}_{a}^{i},\quad i = 1,\dots, N, $$

其中符号 $\partial i$ 表示粒子 $i$ 的接触集合。等式 (2) 和 (3) 同时适用于有摩擦和无摩擦粒子。在后一种情况下，法线方向上只有一个力分量

$$ \mathbf{f}_{a}^{i} = -f_{a}^{i}\hat{\mathbf{n}}_{a}^{i}\quad(\text{无摩擦}) $$

其中 $\hat{\mathbf{n}}_{a}^{i}$ 表示接触点的法向单位向量，它取决于粒子的形状。对于有摩擦粒子，我们可以将 $\mathbf{f}_{a}^{i}$ 分解为法向分量 $f_{a,n}^{i}$ 和切向的力矢量 $f_{a,\tau}^{i}$（见图 2）。摩擦系数为 $\mu$ 的 $\text{Coulomb}$ 定律用不等式表示为

$$ |f_{a,\tau}^{i}|\leq \mu f_{a,n}^{i}\quad(\text{有摩擦}). $$

---

If the interparticle forces are purely repulsive, as in most of the cases treated in this review, we also have the condition

$$ \mathbf{d}_{a}^{i}\cdot\mathbf{f}_{a}^{i} < 0. $$

如果粒子间的作用力是纯粹的排斥力，就像本综述中讨论的大多数情况一样，我们还需要满足以下条件

$$ \mathbf{d}_{a}^{i}\cdot\mathbf{f}_{a}^{i} < 0. $$

这里点乘表示力线与力的夹角大于 $90^{\circ}$.

Finally, Newton’s third law implies that two particles $i$ and $j$ in contact with $a$ satisfy

$$ \mathbf{f}_{a}^{i} = -\mathbf{f}_{a}^{j} $$

最后，牛顿第三定律意味着与 $a$ 接触的两个粒子 $i$ 和 $j$ 满足以下条件

$$ \mathbf{f}_{a}^{i} = -\mathbf{f}_{a}^{j} $$

Metastability of jammed states

Having defined the necessary and sufficient conditions for a granular system to be jammed, we now provide a finer description of jammed states, based on the concept of metastability, i.e., their stability with respect to particles displacements.

A characterization similar to the one proposed here appeared already in Torquato and Stillinger (2001), where the concept of jamming categories for metastable packings has been defined. The similarities with the classification of the jammed states in Torquato and Stillinger (2001) are discussed in parallel with the classification presented next.

在定义了颗粒系统发生堵塞的必要条件和充分条件之后，我们现在根据亚稳性的概念，即颗粒位移的稳定性，对堵塞态进行更精细的描述。

Torquato 和 Stillinger（2001 年）已经提出了与本文类似的描述，并定义了亚稳态堆积的堵塞类别概念。在讨论 Torquato 和 Stillinger（2001 年）中堵塞状态分类的相似之处的同时，我们还将讨论接下来介绍的分类方法。

---

To properly define the metastable jammed states we need to specify with respect to what type of displacements they are metastable. More precisely, if we start from an initially jammed state satisfying Eqs. (1)–(7) and then displace a set of particles, how do we decide if the initial state is stable under this move? A helpful discriminant is the volume $V$ or equivalently the volume fraction of the packing $\phi$ defined as the ratio of the volume occupied by the particles to the total volume of the system and the number of particles involved in the displacement.

要正确定义亚稳态的堵塞态，我们需要明确它们在哪种位移下是亚稳态。更确切地说，如果我们从满足式（1）-（7）的初始堵塞状态开始，然后位移一组粒子，我们如何判断初始状态在此位移后是否稳定？一个有用的判别因素是体积 $V$，或者等价于堆积的体积分数 $\phi$，定义为粒子所占体积与系统总体积之比，以及参与位移的粒子数量。

Thus, consider an initially jammed state and assume you can displace only one particle at a time. If the volume fraction of the packing is not increasing whatever particle you move, then we may assert that the packing is stable against any single particle displacement. We call this type of jammed state a 1-particle-displacement (1-PD) metastable jammed state, which is defined as a configuration whose volume fraction cannot be increased by the displacement of one single particle; see Fig. 3(a).

因此，考虑初始堵塞状态，假设每次只能移动一个粒子。如果无论移动哪个粒子，堆积的体积分数都不会增加，那么我们就可以断言，堆积在任何单粒子位移情况下都是稳定的。我们将这种堵塞态称为 “单粒子位移（1-PD）亚稳堵塞态”，其定义是：单粒子位移无法增加其体积分数的构型；见图 3(a)。

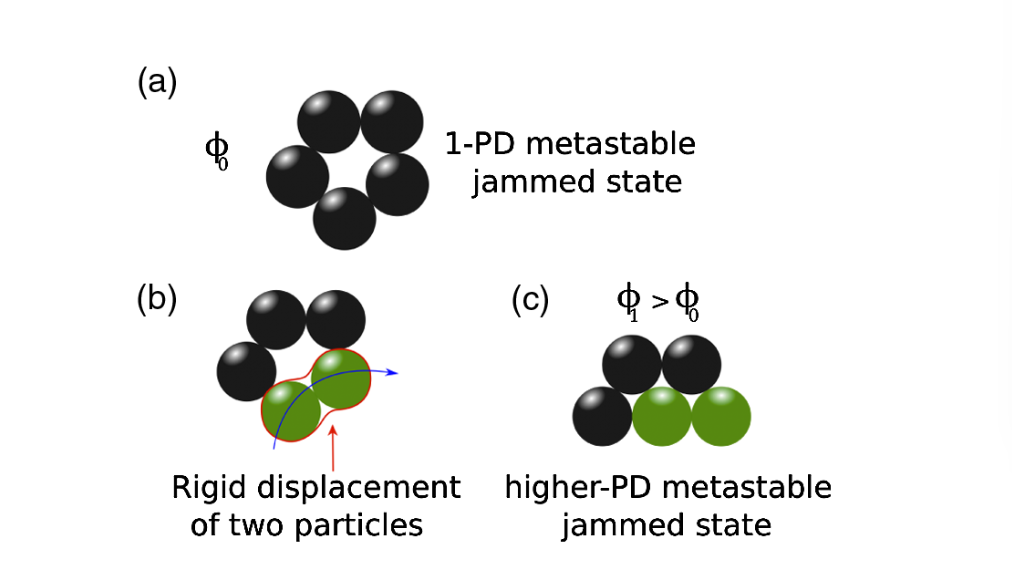
(a) Example of a 1-particle-displacement jammed state: no particle can increase the volume fraction by displacing itself while keeping the others fixed in their positions. It is assumed that a membrane is keeping the particles in place or that they are surrounded and kept in place by a rigid container.

(b) The 1-PD metastable state in (a) is not stable under 2-PD. Simultaneous displacement of two particles to escape the 1-PD metastable trap, two contacting particles are displaced while keeping the others fixed in their positions.

(c) Higher-order metastable jammed state: after the move in (b), a new metastable jammed state is reached having higher stability than the original one in (a).

(a) 单粒子位移堵塞状态示例：没有粒子能通过自身位移来增加体积分数，而其他粒子的位置保持不变。假设有一层薄膜将粒子固定在原位，或者粒子被一个坚硬的容器包围并固定在原位。

(b) (a) 中的 1-PD 亚稳状态在 2-PD 下并不稳定。两个粒子的同时位移 为了逃离 1-PD 亚稳阱，两个接触的粒子要发生位移，而其他粒子的位置要保持不变。

(c) 高阶亚稳堵塞状态：经过（b）中的移动后，会达到一个新的亚稳堵塞状态，其稳定性高于（a）中的原始状态。

However, $\phi$ may be increased by moving a set of two or more particles at the same time. The definition of 1-PD metastable jammed states is the same as the definition of local jamming in Torquato and Stillinger (2001), stating that in a locally jammed configuration no single particle can be displaced while keeping the positions of all other particles fixed.

然而，$\phi$ 可以通过同时移动一组两个或更多粒子而增加。1-PD 亚稳堵塞态的定义与 Torquato 和 Stillinger（2001 年）中局部堵塞的定义相同，即在局部堵塞构型中，在保持所有其他粒子位置固定的情况下，不能移动任何一个粒子。

---

We can now extend this definition to jammed states which are stable with respect to the simultaneous displacement of multiple particles. Specifically, we define a k-particledisplacement ($k$-PD) metastable jammed state as a configuration whose volume fraction cannot be increased by the simultaneous displacement of any contacting subset of $1,2,\dots,k$ particles.

现在, 我们可以将这一定义扩展到与多个粒子同时位移有关的稳定的堵塞态. 具体来说，我们将 $k$ 个粒子同时位移（$k$-PD）的亚稳堵塞态定义为这样一种构型: 它的体积分数不会因为任意接触的 $1,2,\dots,k$ 粒子子集的同时位移而增加。

Again, we find this definition quite similar to the definition of the collective jamming category in Torquato and Stillinger (2001), which states that in collectively jammed configurations no subset of particles can be simultaneously displaced so that its members move out of contact with one another and with the remaining set.

同样，我们发现这一定义与 Torquato 和 Stillinger（2001 年）对集体堵塞类别的定义十分相似，即在集体堵塞构型中，没有任何一个颗粒子集可以同步位移从而使其成员彼此之间以及与其余颗粒子集脱离接触。

Following the definitions given above a ground state of the system is a configuration whose volume fraction cannot be increased by the simultaneous displacement of any finite number of particles. A ground state of jamming corresponds to the $k\rightarrow\infty$ limit of a $k$-PD metastable jammed state, the $\infty$-PD jammed ground state.

根据上面给出的定义, 系统的基态是指, 任何有限数量粒子的同时位移, 都不能使其体积分数增加的构型. 堵塞的基态对应于$k$-PD亚稳堵塞态的 $k\rightarrow\infty$ 极限，即 $\infty$ -PD堵塞基态。

---

In the following section we introduce the volume function $\mathcal{W}(\mathbf{r})$ to parametrize the system volume as a function of the particles’ positions. It is useful then to classify the $k$-PD metastable jammed states in terms of the minima of this function.

More precisely, we identify the $k$-PD metastable jammed states as those states that satisfy the geometrical and mechanical constraints and are local minima of $\mathcal{W}(\mathbf{r})$.

在下一节中，我们将引入体积函数 $\mathcal{W}(\mathbf{r})$ 来将系统体积参数化为粒子位置的函数。因此，根据该函数的最小值对 $k$-PD 亚稳堵塞态进行分类是非常有用的。

更准确地说，我们将 $k$-PD 亚稳堵塞态定义为那些满足几何和力学约束条件, 并且满足 $\mathcal{W}(\mathbf{r})$ 取极小值的态。

For example, 1-PD metastable states are those configurations $\mathbf{r}^{*}$ for which $\mathcal{W}(\mathbf{r})$ is convex around $\mathbf{r}^{*}$ under 1-particle displacements, but nonconvex under k-particle displacements with $k > 1$; see Fig. 4(a).

Here convex means that all the eigenvalues of the Hessian of $\mathcal{W}(\mathbf{r})$ evaluated at the configurations $\mathbf{r}^{*}$ are positive, while nonconvex means that there exists at least one negative eigenvalue in the spectrum of the Hessian.

Similarly, k-PD metastable states are those configurations $\mathbf{r}^{*}$ for which $\mathcal{W}$ is convex around $\mathbf{r}^{*}$ under any k’-particle displacements with $k’ < k$, and nonconvex under any k’-particle displacements with $k’ > k$. A simple example of a 1-PD metastable jammed state is shown in Fig. 3(a).

例如，$1$-PD 亚稳态是那些 $\mathbf{r}^{*}$ 的构型，对于这些构型，$\mathcal{W}(\mathbf{r})$ 在 $1$ 粒子位移下围绕 $\mathbf{r}^{*}$ 是凸的，但在 $k$ 粒子位移（$k > 1$）下是不凸的；见图 4(a)。

同样，$k$-PD 亚稳态是那些 $\mathbf{r}^{*}$ 的构型，对于这些构型的 $\mathcal{W}$, 在 $\mathbf{r}^{*}$ 邻域内, 任何 $k’$-粒子位移（$k’ < k$）表现为凸，而任何 $k’$-粒子位移（$k’ > k$）都表现为不凸。图 3(a) 显示了一个简单的 $1$-PD 亚稳堵塞态实例。

---

Interestingly, in spin-glass systems the (energetically) metastable states can be defined in a similar way, not with respect to volume but to energy. The analog of the 1-PD metastable jammed state is, for a spin glass, the one-spin-flip (1-SF) metastable state, defined as a configuration whose energy cannot be lowered by the flip of any single spin. Similarly the k-spin-flip (k-SF) metastable state, akin to the k-PD metastable jammed state, is a configuration whose energy cannot be lowered by the flip of any cluster of 1; 2; …;kspins.

有趣的是，在自旋玻璃系统中，（能量上的）亚稳态也可以用类似的方法定义，但不是以体积而是以能量来定义。对于自旋玻璃来说，类比于 1-PD 亚稳堵塞态的是单自旋翻转（1-SF）亚稳态，它被定义为一种能量不能因任何单个自旋的翻转而降低的构型。同样，k-自旋-翻转（k-SF）亚稳态与 $k$-PD 亚稳堵塞态类似，是指其能量不能因任何 $1,2,\dots,k$ 个自旋簇的翻转而降低的构型。

Moreover, for spin glasses, several rigorous results on metastable states are known, including their probabilities, basins of attraction, and how they are sampled by various dynamics (Newman and Stein, 1999). These results are explained in detail in Sec. V along with their granular counterpart. The analogy between grains, hard-sphere glasses, and spin glasses has been reviewed by Dauchot (2007) and is described in Table I and Fig. 4(a).

此外，对于自旋玻璃，人们已经知道一些关于亚稳态的严格结果，包括它们的概率、吸引子领域以及它们如何被各种动力学取样（纽曼和斯坦因，1999 年）。第五节将详细解释这些结果及其颗粒对应结果。Dauchot (2007) 综述了颗粒、硬球玻璃和自旋玻璃之间的类比关系，并在表 I 和图 4(a) 中进行了描述。

---

	颗粒物质	硬玻璃球	自旋玻璃
热力学表述	体积函数 $\mathcal{W}(\mathbf{q})$	密度泛函 $S[\rho(\mathbf{r})]$	哈密顿量 $\mathcal{H}(\mathbf{\sigma})$
拉格朗日乘数	致密度 $X$	压强 $P$	温度 $T$
熵	$\text{Edwards}$熵 $S(V)$	构型熵 $\Sigma$	复杂度 $\Sigma$
亚稳态	$\mathcal{W}(\mathbf{q})$ 极小 + 堵塞约束	$S[\rho(\mathbf{r})]$ 极小	$T=0$ 下 $\mathcal{H}(\mathbf{\sigma})$ 取极小
局部亚稳	$1$-PD		$1$-SF $(T=0)$
集体亚稳	$k$-PD		$k$-SF $(T=0)$
全局亚稳	$\infty$-PD ($0\leq\alpha <1$)	$\phi\in[\phi_{\text{th}}, \phi_{\text{gcp}})$	$\infty$-SF$(T = 0,0\leq\alpha <1)$
基态	$\infty$-PD ($\alpha = 1$)	$\phi_{\text{gcp}}$	$\infty$-SF $(T = 0,\alpha = 1)$

Synoptic view of unifying framework to understand the thermodynamics, relevant observables, and classification of metastable states in granular matter, hard-sphere glasses, and spin glasses. The four categories of jamming are defined according to their metastability: local metastable ($1$-PD, SF stable); collective metastable ($k$-PD, SF stable with finite $1 < k <\infty$); globally metastable ($\infty$-PD, SF stable, but with $0\leq \alpha < 1$, where $\alpha = k/N$ for $k,N\rightarrow\infty$); and the true global ground state ($\infty$-PD, SF stable and $\alpha = 1$).

用统一框架的综合视角来理解颗粒物质、硬球玻璃和自旋玻璃中的热力学、相关可观测量和亚稳态的分类。根据其亚稳性定义了四类堵塞态：局部亚稳态（1-PD，SF 稳定）；集体亚稳态（k-PD，SF 稳定，有限的 $k:1 < k <\infty$）；全局亚稳态（$\infty$-PD，SF 稳定，但 $0\leq \alpha < 1$, 其中 $\alpha = k/N$ 且 $k,N\rightarrow\infty$）; 以及真正的全局基态（$\infty$-PD，SF 稳态且 $\alpha = 1$）。

---

Protocols to generate jammed packings usually lead to a nonzero fraction of particles ($2$%–$5$%), which remain mobile even though all other particles are $\infty$-PD jammed. These particles are called rattlers and can be displaced within a cage without changing the volume function.

通常，生成堵塞堆积的协议会导致一部分非零分数的颗粒（2%-5%）仍然可以移动，即使所有其他颗粒都被 $\infty$-PD 堵塞。这些颗粒被称为 “跃迁子”（rattlers），可以在不改变体积函数的情况下在笼子中移动。

Now that we have a rigorous definition for the jammed states and their metastable classification, we address the crucial problem of how to describe their statistical mechanics. Consider a granular material undergoing vertical tapping. After tapping, the system relaxes into a jammed state. Subsequent tapping will allow the system to explore other jammed states. An important question arises: how does the tapping dynamics sample the jammed states or what is the probability measure for jammed states obtained from tapping?

现在，我们已经有了关于堵塞态及其亚稳态分类的严格定义，我们要解决的关键问题是, 如何描述它们的统计力学性质。考虑一种正在进行垂直敲击的颗粒材料。敲击后，系统弛豫进入堵塞状态。随后的敲击将使系统探索其他的堵塞状态。这就产生了一个重要问题：敲击动力学过程是如何对堵塞状态进行采样的，或者从敲击中获得的堵塞状态的概率度量是什么？

Edwards statistical ensemble for granular matter

In 1989 Edwards made the remarkable proposal that the macroscopic properties of static granular matter can be calculated as ensemble averages over equiprobable jammed microstates controlled by the system volume (Edwards and Oakeshott, 1989). The thermodynamics of powders was created with this claim (Edwards, 1994):

“We assume that when $N$ grains occupy a volume $V$ they do so in such a way that all configurations are equally weighted. We assume this; it is the analog of the ergodic hypothesis of conventional thermal physics.”

1989 年，Edwards 提出了一个非凡的建议，即静态颗粒物质的宏观特性可以通过由系统体积控制的可等价堵塞微观态的系综平均值来计算（Edwards 和 Oakeshott, 1989 年）。粉末热力学正是基于这一观点而诞生的（Edwards，1994 年）:

“我们假设，当 $N$ 个颗粒占据某体积 $V$ 时，所有构型的权重相同。我们的假设与传统热物理学中的遍历假设类似.”

---

This idea is suggestive because it turns a complicated dynamical problem into a relatively simpler equilibrium problem. Such an equilibrium sampling in a nonequilibrium system was recently also adopted by several authors in the glass community to study the ground state of amorphous packings as the infinite-pressure limit of metastable glassy states described by equilibrium statistical mechanics (Parisi and Zamponi, 2010; Charbonneau et al., 2017).

Here, in the so-called Monasson construction (Monasson, 1995), a modified equilibrium average over metastable states is taken, supplemented by the additional assumption that such metastable states become jammed states in the infinite-pressure limit.

这一想法很有启发性，因为它将复杂的动力学问题转化为相对简单的平衡问题。最近，玻璃学界的几位学者也采用了这种非平衡态系统中的平衡态采样方法，将非晶堆积的基态作为平衡统计力学所描述的玻璃态亚稳的压力无限大极限来研究（Parisi 和 Zamponi，2010 年；Charbonneau 等人，2017 年）。

在这里，在所谓的莫纳森构造（Monasson，1995 年）中，对亚稳态进行了修正的平衡平均，并补充了一个额外的假设，即这些亚稳态在无穷压极限时会变成堵塞态。

In such a limit, the states are flatly sampled and the Monasson construction is exactly the Edwards ensemble.

Even more, it turns out that mean-field glass models relaxing at zero temperature have exactly Edwards ergodicity property (Kurchan, 2001): at long times any nonequilibrium observable is correctly given by the typical value it takes over all local energy minima of the appropriate energy density.

The original idea put forward by Edwards is basically to take the flat average at the end, i.e., in the jammed state.

在这样的极限中，状态是平直采样的，Monasson 构造正是 Edwards 系综。

更有甚者，事实证明，在零温度下弛豫的平均场玻璃模型恰恰具有 Edwards 的遍历性（Kurchan，2001 年）：在长时间内，任何非平衡观测值都是由它在适当能量密度的所有局域能量极小值上所取的典型值正确给出的。

Edwards 提出的最初想法基本上是在最后(即在堵塞状态下)才取平直平均值。

---

Under the Edwards ergodic hypothesis, granular matter should be amenable to an equilibrium statistical mechanical treatment, where the role of energy is played by the volume, and all the jammed states at a fixed volume are equally probable.

In granular assemblies consisting of dry particles in a size range above a few microns, the thermal energy at room temperature can be neglected and neither equilibrium entropy nor free energy can be used as thermodynamic potentials to describe the system.

Nevertheless, for large enough particle numbers, statistical ideas seem relevant: macroscopic observables such as the packing fraction are robustly reproduced for a given protocol.

根据 Edwards 的遍历假说，颗粒物质应该可以用平衡统计力学处理，其中能量的作用由体积来发挥，在固定体积下的所有堵塞状态都具有相同的可能性。

在由尺寸范围超过几微米的干燥颗粒组成的颗粒集合体中，室温下的热能可以忽略不计，平衡熵和自由能都不能用作描述系统的热力学势。

尽管如此，对于足够大的颗粒数，统计思想似乎是相关的：在给定的协议下，堆积分数等宏观可观测量可以被稳定复现。

If operations manipulating individual particles are neglected, granular assemblies are thus described by well-defined macrostates that correspond to many different microscopic configurations. Instead of the energy, one can equivalently take the volume as the key variable characterizing the macrostate of a static assembly.

S. F. Edwards insight suggested to consider the volume of a granular assembly analogous to the energy of an equilibrium system: unlike in typical equilibrium systems, the volume is not an externally fixed parameter, but depends on the microscopic configuration of the particles including positions and orientations.

This suggests to introduce a volume function $\mathcal{W}(\{\mathbf{r}_{i},\hat{\mathbf{t}}_{i}\})$ giving the system volume as a function of the particles positions $\mathbf{r}_{i}$ and orientations $\hat{\mathbf{t}}_{i}$ equivalent to the Hamiltonian $\mathcal{H}(\mathbf{p}_{i},\mathbf{r}_{i}),i = 1,\dots,N$.

如果忽略对单个粒子的操作，颗粒集合体就可以用定义明确的宏观状态来描述，这些宏观状态对应于许多不同的微观构型。我们可以将体积, 而非能量, 作为表征静态装配宏观状态的关键变量.

S. F. Edwards 的洞察力建议将颗粒集合体的体积类比于平衡态系统的能量; 与典型的平衡态系统不同，体积不是一个外部固定参数，而是取决于颗粒的微观构型，包括位置和取向。

这就需要引入一个体积函数 $\mathcal{W}(\{\mathbf{r}_{i},\hat{\mathbf{t}}_{i}\})$ 给出系统体积, 作为粒子位置 $\mathbf{r}_{i}$ 和方向 $\hat{\mathbf{t}}_{i}$ 的函数，相当于哈密顿方程 $\mathcal{H}(\mathbf{p}_{i},\mathbf{r}_{i}),i = 1,\dots,N$.