受迫振动

本节是为了论证: 在小振幅(线性)条件下, 响应效率函数与振幅无关.

设一振子质量为 $m$, 运动阻力为 $f = \alpha v$, 回复力为 $m\omega_{0}^{2}$, 则可建立运动方程

$$ m\frac{\mathrm{d}^2 x}{\mathrm{d}t^{2}} = -m\omega_{0}^{2}x - \alpha\frac{\mathrm{d}x}{\mathrm{d}t} + F_{0}\cos{\omega t} $$

约定 $\beta = \frac{\alpha}{2m}$, $f = \frac{F_{0}}{m}$, 整理为

$$ \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}} + 2\beta\frac{\mathrm{d}x}{\mathrm{d}t} + \omega_{0}^{2}x = f\cos{\omega t} $$

---

先求齐次方程

$$ \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}} + 2\beta\frac{\mathrm{d}x}{\mathrm{d}t} + \omega_{0}^{2}x = 0 $$

即为无阻尼运动. 设特征根 $x = e^{\lambda t}$, 化简得到

$$ \lambda^{2} + 2\beta\lambda + \omega_{0}^{2} = 0 $$

• 欠阻尼($\beta<\omega_{0}$)

则 $\lambda = -\beta + i\sqrt{\omega_{0}^{2}-\beta^{2}} = -\beta + i\omega^{\prime}$. 因此齐次方程的通解为

$$ \widetilde{x}_{c}(t) = e^{-\beta t}\left(\widetilde{A}_{1}e^{i\omega^{\prime}t} + \widetilde{A}_{2}e^{-i\omega^{\prime}t}\right) $$

取其实部即为

$$ x_{c}(t) = x_{0}e^{-\beta t}\cos{(\omega^{\prime} t + \phi)} $$

• 过阻尼($\beta > \omega_{0}$)

则特征根为 $\lambda = -\beta + \sqrt{\beta^{2} - \omega_{0}^{2}}$, 位置函数为其线性组合:

$$ x_{c}(t) = A_{1}e^{-\lambda_{1}t} + A_{2}e^{-\lambda_{2}t} $$

---

现在继续求解非齐次方程. 设特解 $x_{p}(t) = \widetilde{K}e^{i\omega t}$, 则得到

$$ (-\omega^{2} + 2\beta\omega i + \omega_{0}^{2})\widetilde{K}e^{i\omega t} = fe^{i\omega t} $$

$\widetilde{K}$ 和 $t$ 无关, 因此

$$ \widetilde{K} = \frac{f}{-\omega^{2} + 2\beta\omega i + \omega_{0}^{2}}\Rightarrow \widetilde{x}_{p}(t) = \frac{f}{-\omega^{2} + 2\beta\omega i + \omega_{0}^{2}} e^{i\omega t} $$

对 $\widetilde{x}_{p}(t)$ 进行分母有理化以得到实部:

$$ \widetilde{x}_{p}(t) = \frac{f(\omega_{0}^{2}-\omega^{2} - 2\beta\omega i)}{(\omega_{0}^{2} - \omega^{2})^{2} - 4\beta^{2}\omega^{2}}e^{i\omega t}\\ \Rightarrow x_{p}(t) = \frac{f}{(\omega_{0}^{2} - \omega^{2})^{2} + 4\beta^{2}\omega^{2}}[(\omega_{0}^{2} - \omega^{2})\cos{\omega t} + 2\beta\omega\sin{\omega t}] = \frac{f}{(\omega_{0}^{2} - \omega^{2})^{2} + 4\beta^{2}\omega^{2}} \cos{(\omega t - \phi)} $$

---

位移函数即为 $x(t) = x_{c}(t) + x_{p}(t)$. 在 $t\rightarrow \infty$ 极限下, 即有

$$ \boxed{\lim_{t\rightarrow\infty}x(t) = \frac{f}{(\omega_{0}^{2} - \omega^{2})^{2} + 4\beta^{2}\omega^{2}} \cos{(\omega t - \phi)}} $$

在 $2\beta^{2} < \omega_{0}^{2}$ 时, 即出现共振现象.

$$ \omega_{\text{res}} = \sqrt{\omega_{0}^{2} - 2\beta^{2}} $$

$\omega_{\text{res}} < \omega_{0}$. 即阻尼的强度决定共振频率与固有频率的偏差值.

我们的 G150 探头是 $f_{\text{res}} = 129.2\text{ kHz}$, $f_{0} = 150\text{ kHz}$. 因此有 $\beta\approx 338.57\text{ k}$

声波测量原理

接收器表面声压 $p$ 和 入射声压 $p_{i}$

…由于在测量或研究空间某一位置的声场时, 总要把接收器置入于声场中, 这时入射到接收器表面的声波在此面上产生一个声压, 在声压的作用下, 接收器的机械系统发生振动, 这一机械振动又以某种方式转换为电振动, 产生正比于接收器表面声压的电压, 这就是声波的接收过程…

一般情况下, 作用于接收器表面的声压, 并不等于入射波的声压… –许肖梅, 声学原理

接收器的机械阻抗通常很大, 可以近似为 “硬边界”. 设 $\dot{\xi}_{i}$ 为入射波在接收器表面上产生的振速, $\dot{\xi}_{r}$ 为散射波在接收器表面产生的振速, 则应有

$$ \dot{\xi}_{i} + \dot{\xi}_{r} = \mathbf{0} $$

辐射声波时, 介质对声源有反作用力

$$ F_{r} = -\dot{\xi}_{r}Z_{S} $$

$Z_{S}$: 二次辐射的辐射阻抗, $\dot{\xi}_{r}$: 辐射器表面的振速.

对接收器, 其所受的作用力即为

$$ F = -\dot{\xi}_{r}Z_{S} = \dot{\xi}_{i}Z_{S} $$

设入射波在接收面上的声压等于 $p_{i}$, 接收面面积为 $S$, 则接收面所受合力为

$$ F = p_{i}S + \dot{\xi}_{1}Z_{S} $$

因接收端离声源较远, 因此将入射波近似为平面波:

$$ \dot{\xi}_{i} = \frac{p_{i}}{\rho_{0}c_{0}} $$

将其代入 $F$ 的表达式, 即有声压为接收面上所受的平均压力:

$$ p = \frac{F}{S} = p_{i} = \left(1 + \frac{Z_{S}}{\rho_{0}c_{0}S}\right) = \widetilde{K}\cdot p_{i} $$

$\widetilde{K} = 1 + \frac{Z_{S}}{\rho_{0}c_{0}S}$, $Z_{S}\in\mathbb{C}\rightarrow \widetilde{K}\in\mathbb{C}$.

这意味着不仅强度不同, 相位也发生了改变.

设圆面半径为 $a$.

• 当 $ka\ll 1$ 时, 其辐射阻抗为

$$ Z_{S} = r_{S} + ix_{S}\approx \rho_{0}c_{0}S\frac{(ka)^{2}}{2} + i\rho_{0}c_{0}S\frac{8ka}{3\pi} $$

则

$$ \widetilde{K} = 1 + \frac{Z_{S}}{\rho_{0}c_{0}S}\approx 1 + \frac{(ka)^{2}}{2} + i\frac{8ka}{3\pi} $$

所以

$$ \lim_{ka\ll 1}\widetilde{K} = 1 $$

• 当 $ka\gg 1$ 时, 其辐射阻抗为

$$ Z_{S} = \rho_{0}c_{0}S $$

所以

$$ \lim_{ka\gg 1}\widetilde{K} = 2 $$

比较完整的 $2a/\lambda$ 域分布:

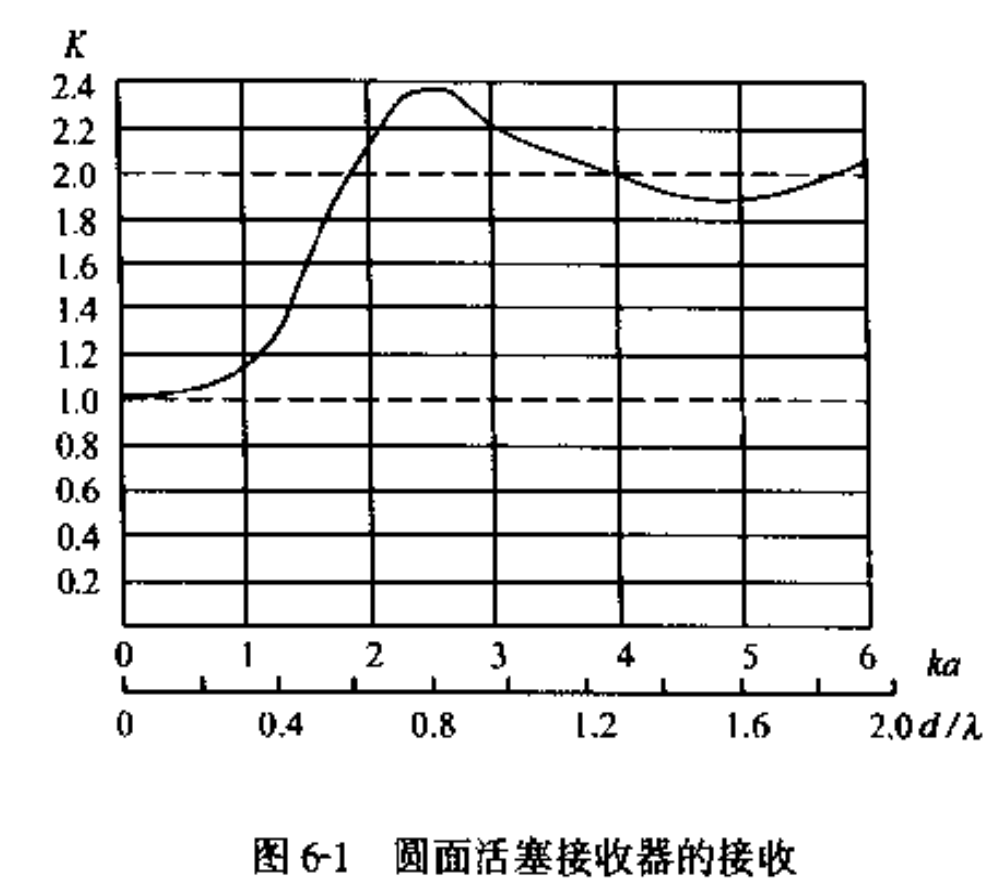
进行简单的估算: 贾老师的探测面直径 $d = 30\text{ mm}$, $\lambda_{E}\approx \frac{1000\text{ m/s}}{500\text{ kHz}} = 2\text{mm}$. 则 $d/\lambda \approx 15\gg 1$, 即应当采用短波极限. (当然, 实际上是在很宽的频域内分析的, 所以这也是响应函数的一部分)

与声波波长相比, 接收器的尺寸越小, 其声场畸变越小. 在各类形状因素中, 又以球形接收器最小.

以上结论是接收器为圆面导出的, 但是在其他普通情况下, 也有类似的结论.

畸变与失真

$p = \widetilde{K}p_{i}$

需要注意的是, 由于辐射阻抗 $Z_{S} = Z_{S}(f)$, 所以 $\widetilde{K} = \widetilde{K}(f)$. 我们需要从频域分析来回答畸变的问题.

令自由场中声压为 $p_{i}(t)$. 则频域分布为

$$ F(\omega) = \int_{-\infty}^{+\infty}p_{i}(t)e^{-i\omega t}\mathrm{d}t $$

反变换:

$$ p_{i}(t) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{i\omega t}\mathrm{d}\omega $$

接收声压为

$$ p(t) = p_{i}(t)\widetilde{K}(\omega) $$

其频谱密度为

$$ \begin{aligned} F(\omega) &= \int_{-\infty}^{+\infty}p_{i}(\omega)\widetilde{K}(\omega)e^{-i\omega t}\mathrm{d}t\\ &= \widetilde{K}(\omega)\int_{-\infty}^{+\infty}p_{i}(t)e^{-i\omega t}\mathrm{d}t = \widetilde{K}(\omega)F_{i}(\omega) \end{aligned} $$

反变换为

$$ p(t) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{i\omega t}\mathrm{d}\omega = \frac{1}{2\pi} \int_{-\infty}^{+\infty}\widetilde{K}(\omega)F(\omega)e^{i\omega t}\mathrm{d}\omega $$

所以接收器接收到的波形 $p(t)$ 一般都不同于入射波形 $p_{i}(t)$.

假定压电效应呈线性($即p\propto U$), 同时考虑两次散射, 即有

$$ U(\omega) = \widetilde{K}^{2}(\omega)U_{0}(\omega) $$

使用频率为 $f_{i} = \frac{\omega_{i}}{2\pi}$ 的正弦连续波激励发射探头, 接收探头得到离散信号分布 $G(\{f_{i}\})$, 即可间接测定 $\widetilde{K}(f)$.

为了避免接收失真, 需要考虑探头尺度和接收信号之间的相性. 令 $f_{b}$ 为入射声波频域内最高频率成分, 则对应波长

$$ \lambda_{b} = \frac{c}{f_{b}} $$

为各成分中最短的. 观察上插图可知, $\widetilde{K}\approx 1 \Leftarrow \frac{2a}{\lambda} \leq \frac{1}{4}$. 因此有

$$ d\leq \frac{\lambda_{b}}{4} $$

做一个简单的估算: 我们采用的探头尺度为 $d = 19\text{ mm}$, 则最短波长为 $f_{b}\approx 4\times 19\text{ mm} \approx 80\text{ mm}$, 而目前所做的实验等效波长 $\lambda_{E}$ ~ $nd_{i}\approx 10^{1}\text{ mm}$, 这显然是无法满足的. 也就是说, 对于这一部分响应函数也是需要考虑的.

响应与指向

一个接收器在给定的频率下, 单位平面波声压所产生的开路电压, 即为此接收器在该给定频率下的响应/灵敏度.

注意: 接收器表面的实际声压与接收器没有放入声场时该点的自由场声压不同, 所以需要分开谈论.

1. 实际声压响应.

$$ M_{e} = \frac{V(\theta,\varphi)}{p(\theta,\varphi)} $$

$M_{e}$: 实际声压响应($\text{V}/\mu\text{bar}$); $V$: 接收器开路电压($\text{V}$); $p$: 接收器表面实际声压($\mu\text{bar}=\text{dyn/cm}^{2}$).

2. 自由场响应

如果单位平面波声压指的是在接收器放入声场以前被测点的自由场声压, 此时接收器而对响应为自由场响应.

$$ M_{F} = \frac{V(\theta,\varphi)}{p_{0}} $$

$V$: 接收器开路电压($\text{V}$); $p_{0}$: 被测点自由场声压($\mu\text{bar}$).

用 $\text{dB}$ 表示接收器的响应:

$$ E_{\text{实际声压}} = 20\log_{10}M_{e} = 20\log_{10}\frac{V}{p}\\ E_{\text{自由场}} = 20\log_{10}M_{F} = 20\log_{10}\frac{V}{p_{0}} $$

接收器的方向特性可用接收器的自由场相对响应来表示. 选取接收器最大相应方向为参考方向, 以球坐标表示即有

$$ R(\theta, \varphi) = \frac{M_{F}(\theta, \varphi)}{M_{F}(0,0)} = \frac{V(\theta, \varphi)}{V(0,0)} $$

因为 $p_{0}$ 被消去了, 所以 $R$ 也被称作 相对电压响应.

阵元法求解相对响应函数

一维阵元

设 $n$ ($n = 2k + 1,k\in\mathbb{Z}$) 个相同的点接收器以等距 $d$ 排成直线.

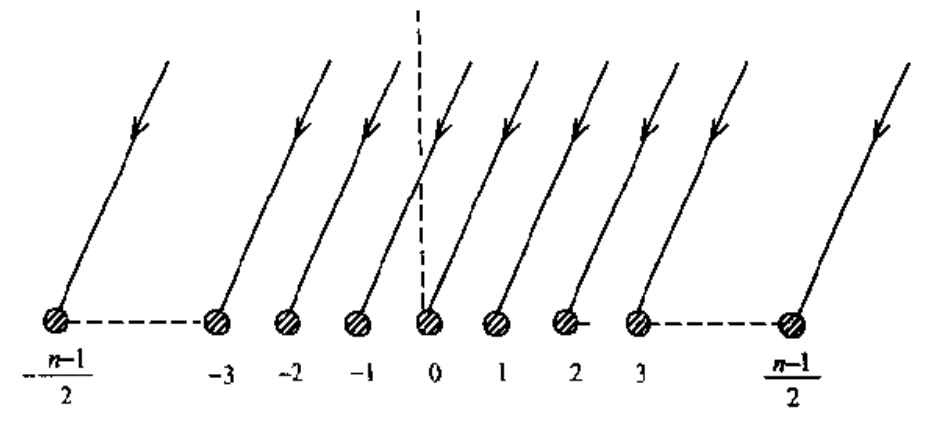
令一平面波与阵法线成 $\theta$ 角入射, 则阵元间存在 “声程差”. $+1$ 阵元与 $0$ 阵元的声程差为

$$ l_{1} = d\sin{\theta} $$

对应的相差为

$$ \phi_{1} = \omega\frac{d\sin{\theta}}{c} $$

类似的, 写出 $+\frac{n-1}{2}$ 阵元与 $0$ 阵元的声程差及其相差为

$$ l_{\frac{n-1}{2}} = \frac{n-1}{2}d\sin{\theta},\quad \phi_{\frac{n-1}{2}} = \omega\frac{n-1}{2}\frac{d\sin{\theta}}{c} = \frac{(n-1)\pi}{\lambda}d\sin{\theta} $$

假定各阵元的声压响应都为 $M_{0}$, 总输出电压为阵元输出电压之和. 则

$$ V(\theta) = M_{0}p_{0}\frac{\sin{\left(\frac{n\pi}{\lambda}d\sin{\theta}\right)}}{\sin{\left(\frac{\pi}{\lambda}d\sin{\theta}\right)}} $$

显然, 如果声波垂直入射($\theta = 0$), 则声程差为 $0$, 总信号为

$$ V(0) = M_{0}p_{0}n $$

所以相对响应为

$$ R(\theta) = \frac{V(\theta)}{V(0)} = \frac{\sin{\left(\frac{n\pi}{\lambda}d\sin{\theta}\right)}}{n\sin{\left(\frac{\pi}{\lambda}d\sin{\theta}\right)}} $$

其函数形式与衍射光栅中的干涉因子 $I$(更准确的说是 $\sqrt{I}$, 因为光强需要对幅值进行平方) 相同.

这就是接收器的指向性.

若采用 $n\rightarrow \infty$ 极限, 则离散阵化为连续阵. 设长 $L$ 的连续直线接收器的声压响应为 $M(\theta, \varphi)$, 则 $d\rightarrow 0, nd=L$:

$$ V(\theta) = M(\theta, \varphi)p = M(\theta, \varphi)p_{0}\frac{\sin{\left(\frac{\pi L}{\lambda}\sin{\theta}\right)}}{\frac{\pi L}{\lambda}\sin{\theta}}\Rightarrow R(\theta) = \frac{\sin{\left(\frac{\pi L}{\lambda}\sin{\theta}\right)}}{\frac{\pi L}{\lambda}\sin{\theta}} $$

圆形活塞式接收器

考虑接收器散射波的影响, 有

$$ R(\theta, \varphi) = \frac{P(\theta, \varphi)}{P(0,0)} $$

$P(\theta, \varphi)$ 和 $P(0,0)$ 均为实际声压. $P(0,0)$ 是声波沿着接收器最大响应方向入射时接收器表面的实际声压; $P(\theta, \varphi)$ 为声波沿着与接收器最大响应方向成 $\theta, \varphi$ 角度入射产生的接收器表面实际声压.

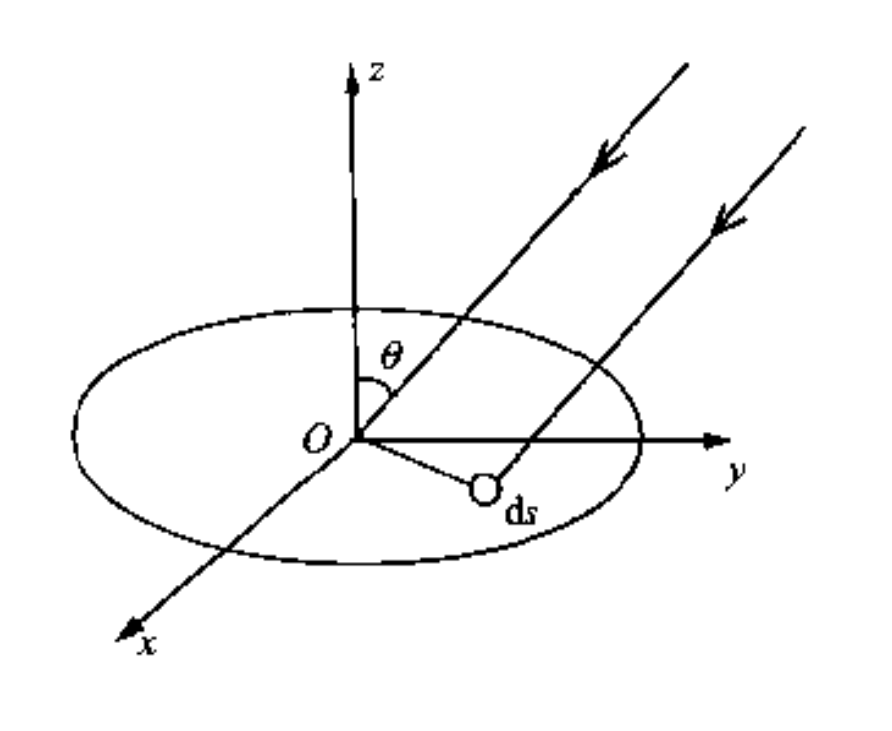
$p_{i}$ 入射波在 $O$ 点的声压; $\dot{\xi}_{i}$: 入射波在 $O$ 点产生的振速; $\theta$: 入射波与接收面法线的夹角.

可以近似接收面上个点幅值相同而相位不同. 设 $\epsilon$ 为面元 $\mathrm{d}S$ 与 $O$ 点处的声程差, 则 $\mathrm{d}S$ 处的声压为

$$ p_{i}e^{-ik\epsilon} $$

振速为

$$ \dot{\xi}_{i}e^{-ik\epsilon} $$

若将接收面视为刚性边界, 则入射波与散射波在法线方向上的振速分量应当相等. 即 $\mathrm{d}S$ 散射波法线方向振速为 $-\dot{\xi}_{i}e^{-ik\epsilon}\cos{\theta}$.

散射波会对接收面产生反作用力, 大小为散射波法线振速乘接收器表面辐射阻抗, 且与接收器法线方向相反:

$$ -(-\dot{\xi}_{i}e^{-ik\epsilon}\cos{\theta})\frac{Z_{S}}{S}\mathrm{d}S = \dot{\xi}_{i}e^{-ik\epsilon}\cos{\theta}\frac{Z_{S}}{S}\mathrm{d}S $$

$Z_{S}$: 整个接收器的辐射阻抗; $S$: 接收器面积; $\frac{Z_{S}}{S}$: 接收面单位面积的辐射阻抗; $\frac{Z_{S}}{S}\mathrm{d}S$: 面元 $\mathrm{d}S$ 的辐射阻抗.

积分得到散射波对接收面的作用力:

$$ F_{S}(\theta) = \iint_{S}\frac{Z_{S}}{S}\dot{\xi}_{i}e^{-ik\epsilon}\cos{\theta}\mathrm{d}S = \frac{Z_{S}}{S}\dot{\xi}_{i}\cos{\theta}\iint_{S}e^{-ik\epsilon}\mathrm{d}S $$

垂直入射($\theta=0$), 即 $\epsilon = 0$. 有

$$ F_{S}(0) = \frac{Z_{S}}{S}\dot{\xi}_{i}\iint_{S}\mathrm{d}S = \frac{Z_{S}}{S}\dot{\xi}_{i}S = Z_{S}\dot{\xi}_{i} $$

平均声压采用为

$$ p_{S}(\theta) = \frac{F_{S}(\theta)}{S} $$

则

$$ \frac{p_{S}(\theta)}{p_{S(0)}} = \frac{F_{S}(\theta)}{F_{S}(0)} = \frac{\dot{\xi}_{i}\cos{\theta}\iint_{S}e^{-ik\epsilon}\mathrm{d}S}{\dot{\xi}_{i}S} = \cos{\theta}\cdot\color{red}{\frac{\iint_{S}e^{-ik\epsilon}\mathrm{d}S}{S}} = \cos{\theta}\cdot \color{red}{R(\theta)} $$

将入射波近似为平面波, 则有

$$ \dot{\xi}_{i} = \frac{p_{i}}{\rho_{0}c_{0}} $$

入射波的作用力 $F_{i}(\theta)$ 为:

$$ F_{i}(\theta) = \iint_{S}p_{i}e^{-ik\epsilon}\mathrm{d}S = p_{i}\iint_{S}e^{-ik\epsilon}\mathrm{d}S $$

垂直入射($\theta = 0$)时, 声程差为 $0$, 有

$$ p_{i}(0) = \iint_{S}p_{i}\mathrm{d}S = p_{i}S $$

一般情况下, 则入射波平均声压为

$$ p_{i}(\theta) = \frac{F_{i}(\theta)}{S} $$

所以

$$ \frac{p_{i}(\theta)}{p_{i}(0)} = \frac{F_{i}(\theta)}{F_{i}(0)} = \frac{\iint_{S}e^{-ik\epsilon}\mathrm{d}S}{S} = R(\theta) $$

接收器表面收到的实际声压 $p(\theta)$ 是入射波与散射波之和:

$$ p(\theta) = p_{i}(\theta) + p_{S}(\theta) = p_{i}(0)R(\theta) + p_{S}\cos{\theta}R(\theta)\\ = [p_{i}(0) + p_{S}(0)\cos{\theta}]R(\theta) = \left[p_{i}(0) + \frac{Z_{S}\dot{\xi}_{i}}{S}\cos{\theta}\right]R(\theta) = p_{i}R(\theta)\left[1 + \frac{Z_{S}\cos{\theta}}{\rho_{0}c_{0}S}\right] $$

垂直入射($\theta = 0$)即有

$$ p(0) = p_{i}(0) + p_{S}(0) = p_{i}\left(1 + \frac{Z_{S}}{\rho_{0}c_{0}S}\right) $$

相对响应

$$ R_{l}(\theta) = \frac{p(\theta)}{p(0)} = \frac{1 + \frac{Z_{S}\cos{\theta}}{\rho_{0}c_{0}S}}{1 + \frac{Z_{S}}{\rho_{0}c_{0}S}}\cdot R(\theta) $$

设圆形活塞式接收器半径为 $a$, 则

• 高频($\lambda \ll a$)

$$ Z_{S}\approx \rho_{0}c_{0}S\Rightarrow R_{l}(\theta) = \frac{1 + \cos{\theta}}{2}R(\theta) $$

• 低频($\lambda \gg a$)

$$ Z_{S}\approx \rho_{0}c_{0}S\frac{(ka)^{2}}{2} + i\rho_{0}c_{0}S\frac{8ka}{3\pi}\Rightarrow Z_{S} = 0 $$

所以

$$ R_{l}(\theta) = R(\theta) $$

噪声

同一方向性的接收器在接收同样的信号时, 若噪声场不同, 则接收到的信号也不同.

假设: 1. 噪声源相位随机, 互不相关; 2. 噪声强度各向同性; 3. 噪声源远离接收系统.

理想流体介质中的声波

三个物理量: 声压 $p$, 振速 $u$, 密度 $\rho$. 运用基本定律推导出三者的关系式.

理想流体的假定条件: 1. 无粘性; 2. 连续性; 3. 均匀性; 4. 绝热性; 5. 无旋性; 6. 微扰性. 因此研究的是小振幅声波在流体介质中的传播规律. 大振幅的声波需要到非线性声学部分研究.

基本方程

运动方程

设介质静止 $u_{0} = 0$, 静止密度为 $\rho_{0}$. 则在 $x$ 轴上, 当声波通过时, 存在振速分布函数 $u(x,y,z,t)$, 压强分布函数 $P_{0} + p(x,y)$. 则体元 $\Delta V$ 在 $x$ 轴上所受合力为

$$ F_{x} = F_{1} - F_{2} = -\Delta P\Delta y\Delta z $$

因为是小振幅波动所以取一阶近似, 有

$$ -\Delta P\Delta y\Delta z = \rho\Delta x\Delta y\Delta z\frac{\partial u_{x}}{\partial t}\rightarrow -\frac{\Delta P}{\Delta x} = \rho\frac{\partial u_{x}}{\partial t}\rightarrow -\frac{\partial P}{\partial x} = \rho_{0}\frac{\partial u_{x}}{\partial t} $$

应用在 $y$ 轴和 $z$ 轴上后, 合并写作 $\nabla$ 算子的形式:

$$ -\nabla P = -\nabla(p + P_{0}) = \boxed{-\nabla p = \rho_{0}\frac{\mathrm{d}\mathbf{u}}{\mathrm{d}t}} $$

连续性方程

核心思想是流体质量定理. 设 $t$ 时振速分布为 $\mathbf{u}(x,y,z,t)$, 仍以 $x$ 轴为例进行分析.

在 $\Delta t$ 时间内, 流入 $\Delta V$ 的质量为 $\rho u_{x}\Delta y\Delta z\Delta t$ ($\rho u_{x}$ 为单位时间通过单位面积的质量), 流出 $\Delta V$ 的质量为

$$ \left[\rho u_{x} + \frac{\partial }{\partial x}(\rho u_{x})\Delta x\right]\Delta y\Delta z\Delta t $$

那么 $x$ 方向上在 $\Delta t$ 时间的质量增量为

$$ -\frac{\partial }{\partial x}(\rho u_{x})\Delta x\Delta y\Delta z\Delta t $$

体元 $\Delta V$ 内的质量变换量为

$$ \Delta m = \Delta\rho\Delta x\Delta y\Delta z = -\left[\frac{\partial }{\partial x}(\rho u_{x}) + \frac{\partial }{\partial y}(\rho u_{y}) + \frac{\partial }{\partial z}(\rho u_{z})\right]\Delta x\Delta y\Delta z\Delta t $$

消去微元并取极限形式:

$$ \frac{\partial\rho}{\partial t} = -\left[\frac{\partial }{\partial x}(\rho u_{x}) + \frac{\partial }{\partial y}(\rho u_{y}) + \frac{\partial }{\partial z}(\rho u_{z})\right] $$

取小振幅极限 $\rho\approx\rho_{0}$, 即有 $\frac{\partial }{\partial x}(\rho u_{x}) \approx \rho_{0}\frac{\partial u_{x}}{\partial x}$. 同理处理 $y$ 轴和 $z$ 轴, 并合并写作 $\nabla$ 算子形式:

$$ \boxed{\frac{\partial\rho}{\partial t} = -\rho_{0}\nabla\cdot\mathbf{u}} $$

状态方程

因为近似为绝热过程, 因此认为 $P = P(\rho)$. 在静态密度 $\rho_{0}$ 附近进行泰勒展开:

$$ P = P(\rho_{0}) + \left(\frac{\mathrm{d}P}{\mathrm{d}\rho}\right)_{S,\rho_{0}}(\rho - \rho_{0}) + \frac{1}{2!}\left(\frac{\mathrm{d}^{2}P}{\mathrm{d}\rho^{2}}\right)_{S,\rho_{0}}(\rho - \rho_{0})^{2} + \cdots $$

注意到介质膨胀时, $\mathrm{d}P<0, \mathrm{d}\rho < 0$; 介质压缩时, $\mathrm{d}P>0, \mathrm{d}\rho > 0$. 因此 $\left(\frac{\mathrm{d}P}{\mathrm{d}\rho}\right)_{S,\rho_{0}}$ 恒正. 因此设

$$ c^{2} = \left(\frac{\mathrm{d}P}{\mathrm{d}\rho}\right)_{S,\rho_{0}} $$

理想气体绝热状态方程为 $PV^{\gamma} = P_{0}V_{0}^{\gamma}$ (其中 $\gamma = \frac{C_{P}}{C_{V}}$, 空气取 $\gamma=1.4$), 质量守恒有 $M = \rho V = \textit{const.}$, 因此 $\rho V = \rho_{0}V_{0}$. 两者联立有

$$ P = \left(\frac{\rho}{\rho_{0}}\right)^{\gamma}P_{0} = \left(\frac{\rho_{0} + \mathrm{d}\rho}{\rho_{0}}\right)^{\gamma}P_{0} \approx P_{0} + \frac{\gamma P_{0}}{\rho_{0}}\mathrm{d}\rho + \cdots $$

取小振幅近似 $\frac{\mathrm{d}\rho}{\rho_{0}}\ll 1$, 即有

$$ p = P - P_{0} = \mathrm{d}P \approx \left(\frac{\gamma P_{0}}{\rho_{0}}\right)\mathrm{d}\rho = c^{2}\mathrm{d}\rho $$

于是得到理想气体中的声速表达式:

$$ c^{2} = \frac{\gamma P_{0}}{\rho_{0}} $$

将 $p$ 和 $\rho^{\prime}$ 视为 $P$ 和 $\rho$ 的变化量, $\mathrm{d}P = \left(\frac{\mathrm{d}P}{\mathrm{d}\rho}\right)_{S,\rho_{0}}\mathrm{d}\rho$ 两边同时对时间求导, 即有

$$ \frac{\mathrm{d}p}{\mathrm{d}t} = c^{2}\frac{\mathrm{d}\rho^{\prime}}{\mathrm{d}t} $$

在液体中, 则改写为

$$ c = \frac{1}{\sqrt{\beta_{S}\rho_{0}}} $$

$\beta_{S}$ 为绝热体积压缩系数.

波动方程

前面已经知道

$$ -\nabla p = \color{red}{\rho_{0}\frac{\partial\mathbf{u}}{\partial t}}\\ \frac{\partial\rho}{\partial t} = -\rho_{0}\nabla\cdot\mathbf{u}\\ \frac{\mathrm{d}p}{\mathrm{d}t} = c^{2}\frac{\mathrm{d}\rho^{\prime}}{\mathrm{d}t} $$

声学测量中通常关心 $p$ 描述声场. 对第二个式子时间求导:

$$ \frac{\partial^{2}\rho^{\prime}}{\partial t^{2}} + \nabla\cdot\left(\color{red}{\rho_{0}\frac{\partial\mathbf{u}}{\partial t}}\right) = 0 $$

代入第一个式子, 有

$$ \color{green}{\frac{\partial^{2}\rho^{\prime}}{\partial t^{2}}} - \nabla\cdot(\nabla p) = 0 $$

密度变化量的全微分为

$$ \begin{aligned} \frac{\mathrm{d}\rho^{\prime}}{\mathrm{d}t} &= \frac{\partial\rho^{\prime}}{\partial t} + \frac{\partial\rho^{\prime}}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}t} + \frac{\partial\rho^{\prime}}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}t} + \frac{\partial\rho^{\prime}}{\partial z}\frac{\mathrm{d}z}{\mathrm{d}t}\\ &= \frac{\partial\rho^{\prime}}{\partial t} + \left(u_{x}\frac{\partial }{\partial x} + u_{y}\frac{\partial }{\partial y} + u_{z}\frac{\partial }{\partial z}\right)\rho^{\prime}\\ &= \frac{\partial\rho^{\prime}}{\partial t} + (\mathbf{u}\cdot\nabla)\rho^{\prime} \end{aligned} $$

小振幅时 $(\mathbf{u}\cdot\nabla)\rho^{\prime}$ 为二阶小量. 因此有

$$ \frac{\mathrm{d}\rho^{\prime}}{\mathrm{d}t} \approx \frac{\partial \rho^{\prime}}{\partial t}, \frac{\mathrm{d}p}{\mathrm{d}t}\approx \frac{\partial p}{\partial t} $$

因此第三个式子改写为

$$ \frac{\partial p}{\partial t} = c^{2}\frac{\partial\rho^{\prime}}{\partial t}\rightarrow {\frac{\partial^{2}p}{\partial t^{2}}} = c^{2}\color{green}{\frac{\partial^{2}\rho^{\prime}}{\partial t^{2}}} $$

观察绿色项, 得到最后的方程

$$ \boxed{\frac{\partial^{2} p}{\partial t^{2}} = c^{2}\nabla^{2}p} $$

声速度势

振速可以通过运动方程化为积分式得到:

$$ \mathbf{u}(x,y,z,t) = -\frac{1}{\rho_{0}}\int_{0}^{t}\nabla p(x,y,z,t^{\prime})\mathrm{d}t^{\prime} $$

$$ \frac{\partial u_{x}}{\partial y} - \frac{\partial u_{y}}{\partial x} = 0\\ \frac{\partial u_{x}}{\partial z} - \frac{\partial u_{z}}{\partial x} = 0\\ \frac{\partial u_{y}}{\partial z} - \frac{\partial u_{z}}{\partial y} = 0 $$

合并写作旋度形式:

$$ \nabla\times\mathbf{u} = 0 $$

即小振幅声场在理想流体中为 无旋场.

又有 $\nabla\times(\nabla \Psi) = 0$, 因此令 $\mathbf{u} = -\nabla \Psi$.

声波的吸收

介质的黏性吸收

对于平面波传播这类一维问题, 单位面积的黏性力可以表示为速度梯度的线性函数:

$$ F_{\eta} = \eta\frac{\partial u}{\partial x} $$

$\eta$ 即为黏度. 切变黏度 $\eta^{\prime}$, 容变黏度 $\eta^{\prime\prime}$.

$$ \eta = \frac{4}{3}\eta^{\prime} + \eta^{\prime\prime} $$

考虑黏性流体的运动方程变化 $p^{\prime} = -F_{\eta} = -\eta\frac{\partial u}{\partial x}$, 即有

$$ \rho_{0}\frac{\partial^{2}\xi}{\partial t^{2}} = -\frac{\partial p}{\partial x} + \eta\frac{\partial^{3}\xi}{\partial^{2}\partial t} $$

复习: $\mathbf{u}$ 为质元振速, $\mathbf{\xi}$ 为质元相对平衡位置的位移. 即有 $$ \mathbf{u} = \frac{\partial \mathbf{\xi}}{\partial t}. $$

体(绝热)弹性模量 $K_{S}$ 有

$$ K_{S} = -V\frac{\mathrm{d}P}{\mathrm{d}V} $$

用声压 $p$ 来代替 $\mathrm{d}P$, 即有

$$ p = -K_{S}\frac{\mathrm{d}V}{V} = -K_{S}\Delta $$

在平面波情况下, $\Delta = \frac{\mathrm{d}V}{V} = -\frac{\mathrm{d}\rho}{\rho} = \frac{\partial \xi}{\partial x}$. 代入即有

$$ p = -K_{S}\frac{\partial \xi}{\partial x} $$

代入黏性流体介质的运动方程:

$$ \boxed{\rho_{0}\frac{\partial^{2}\xi}{\partial t^{2}} = K_{S}\frac{\partial^{2}\xi}{\partial x^{2}} + \eta\frac{\partial^{3}\xi}{\partial x^{2}\partial t}} $$

写为声速 $c_{0} = \sqrt{\frac{K_{S}}{\rho_{0}}}$ 形式即为

$$ \boxed{\frac{\partial^{2}\xi}{\partial t^{2}} = c_{0}^{2}\frac{\partial^{2}\xi}{\partial x^{2}} + \frac{\eta}{\rho_{0}}\frac{\partial^{3}\xi}{\partial x^{2}\partial t}} $$

---

设简谐声波, 则位移波函数为

$$ \xi(x,t) = \xi_{1}(x)e^{i\omega t}. $$

代入运动方程, 化为 $\xi_{1}$ 的微分方程

$$ -\rho_{0}\omega^{2}\xi_{1} = (K_{S} + i\omega\eta)\frac{\partial^{2}\xi_{1}}{\partial x^{2}} $$

令 $K = K_{S} + i\omega\eta$, 则有

$$ -\rho_{0}\omega^{2}\xi_{1} = K\frac{\partial^{2}\xi_{1}}{\partial x^{2}}\Rightarrow -k^{\prime 2}\xi_{1} = \frac{\partial^{2}\xi_{1}}{\partial x^{2}} $$

$k^{\prime} = \omega\sqrt{\frac{\rho_{0}}{K}} = \frac{\omega}{c} - i \alpha_{\eta}$

所以位移波函数 $\xi(x,t)$ 是两个独立解的线性叠加:

$$ \xi = (A e^{-ik^{\prime}x} + B e^{ik^{\prime}x})e^{i\omega t} $$

---

现在详细计算出声波传播速度 $c$ 与吸收系数 $\alpha_{\eta}$. 即有

$$ K = K_{S}\left(1 + i\omega\frac{\eta}{K_{S}}\right) = K_{S}(1 + i\omega H) $$

代入 $k^{\prime}$ 表达式, 即有方程组

$$ \frac{\omega^{2}}{c^{2}} - \alpha_{\eta}^{2} = \frac{\omega^{2}\rho_{0}}{K_{S}} \frac{1}{1 + \omega^{2}H^{2}}\\ 2 \alpha_{\eta}\frac{\omega}{c} = \frac{\omega^{2}\rho_{0}}{K_{S}} \frac{\omega H}{1 + \omega^{2}H^{2}} $$

即有解

$$ c = \sqrt{\frac{K_{S}}{\rho_{0}}}\sqrt{\frac{2(1 + \omega^{2}H^{2})(\sqrt{1 + \omega^{2}H^{2}} - 1)}{\omega^{2}H^{2}}}\\ \alpha_{\eta} = \omega\sqrt{\frac{\rho_{0}}{K_{S}}}\sqrt{\frac{\sqrt{1 + \omega^{2}H^{2}} - 1}{2(1 + \omega^{2}H^{2})}} $$

$\omega H\ll 1$, 即黏性力相较于弹性力很小时上式退化为

$$ c = \sqrt{\frac{K_{S}}{\rho_{0}}} = c_{0}\\ \alpha_{\eta} = \frac{\omega^{2}}{2\rho_{0}c^{3}}\eta = \frac{\omega^{2}}{2\rho_{0}c^{3}}\left(\frac{4}{3}\eta^{\prime} + \eta^{\prime\prime}\right) $$

可见高频吸收比低频大得多.

论 $\omega H\ll 1$.

$$ \lim_{\omega H\ll 1}\alpha_{\eta}\lambda = \lim_{\omega H\ll 1} 2\pi\frac{\sqrt{1 + \omega^{2}H^{2}} - 1}{\omega H} = \pi\omega H $$

即黏性力相较于弹性力很小, 在一个波长距离上声波的吸收很小, 就可以导出以上近似表达式.

将 $\omega$ 写作 $f$ 形式并忽略容变黏度 $\eta^{\prime\prime}$, 即有

$$ \alpha_{\eta} = \frac{8\pi^{2}\eta^{\prime}}{3\rho_{0}c^{3}}f^{2} $$

介质的热吸收

介质中的温度梯度将导致热传导, 从而产生不可逆的机械-热转变.

设介质中存在温度分布 $T(x,t)$, 因此有温度梯度 $\frac{\partial T}{\partial x}$. 有

$$ Q = -\chi\frac{\partial T}{\partial x} $$

$Q$ 为单位时间通过单位面积的热量, $\chi$ 称为热传导系数.

所以体元 $\Delta x\Delta y\Delta z$ 的热增量为

$$ \left[Q - \left(Q + \frac{\partial Q}{\partial x}\Delta x\right)\right]\Delta y\Delta z\delta t = -\frac{\partial Q}{\partial x}\Delta x\Delta y\Delta z\delta t = \chi\frac{\partial^{2}T}{\partial x^{2}} $$

消去所有微元并化为微分形式:

$$ \boxed{\frac{\partial q}{\partial t} = \frac{\chi}{\rho_{0}}\frac{\partial^{2}T}{\partial x^{2}}} $$

$q$ 为 单位质量 介质的热量.

密度变化 $\mathrm{d}\rho$ 时, 引起变化 $\mathrm{d}T,\mathrm{d}V,\mathrm{d}q$. 将热量变化近似为两个过程: 恒压加热($V_{0}\rightarrow V_{0} + \mathrm{d}V$), 等容加热($V = V_{0} + \mathrm{d}V$ 下, $T_{0} + \mathrm{d}T^{\prime}\rightarrow T_{0} + \mathrm{d}T$):

$$ \begin{aligned} \mathrm{d}q &= \mathrm{d}q_{1} + \mathrm{d}q_{2}\\ \mathrm{d}q_{1} &= \left(\frac{\partial q}{\partial T}\right)_{p}\mathrm{d}T^{\prime} = C_{p}\mathrm{d}T^{\prime}\\ \mathrm{d}q_{2} &= \left(\frac{\partial q}{\partial T}\right)_{V}(\mathrm{d}T - \mathrm{d}T^{\prime}) = C_{V}\mathrm{d}T - C_{V}\mathrm{d}T^{\prime} \end{aligned} $$

所以有

$$ \mathrm{d}q = C_{P}\mathrm{d}T + (C_{p} - C_{V})\mathrm{d}T^{\prime} $$

而 $\mathrm{d}T^{\prime}$ 是恒压条件下 $V_{0}\rightarrow V_{0} + \mathrm{d}V$ 产生的温度增量, 即

$$ \mathrm{d}T^{\prime} = \left(\frac{\partial T}{\partial V}\right)_{P}\mathrm{d}V $$

对于单位质量而言 $\rho V = 1$, 由此

$$ \begin{aligned} \left(\frac{\partial T}{\partial V}\right)\mathrm{d}V &= \left(\frac{\partial T}{\partial \rho}\right)_{P}\left(\frac{\partial \rho}{\partial V}\right)_{P}\mathrm{d}V = \left(\frac{\partial T}{\partial \rho}\right)_{P}\left(\frac{-1}{V^{2}}\right)\mathrm{d}V\\ &= \left(\frac{\partial T}{\partial \rho}\right)_{P}\frac{1}{V}\frac{\mathrm{d}\rho}{\rho} = \left(\frac{\partial T}{\partial \rho}\right)_{P}\mathrm{d}\rho \end{aligned} $$

所以

$$ \mathrm{d}T^{\prime} = \left(\frac{\partial T}{\partial \rho}\right)_{V}\mathrm{d}\rho $$

将 $\mathrm{d}T^{\prime}$ 代入 $\mathrm{d}q$ 的表达式:

$$ \mathrm{d}q = C_{V}\mathrm{d}T + (C_{P} - C_{V})\left(\frac{\partial T}{\partial \rho}\right)_{P}\mathrm{d}\rho $$

两边同时求时间偏导:

$$ \boxed{\frac{\partial q}{\partial t} = C_{V}\frac{\partial T}{\partial t} + C_{V}(\gamma - 1)\frac{\partial \rho}{\partial t}} $$

而密度函数 $\rho(p,T)$ 的全微分:

$$ \mathrm{d}\rho = \left(\frac{\partial \rho}{\partial T}\right)_{p}\mathrm{d}T + \left(\frac{\partial \rho}{\partial p}\right)_{T}\mathrm{d}p $$

因为有声速 $c^{2} = \gamma\left(\frac{\partial p}{\partial \rho}\right)_{T}$, 即有

$$ \boxed{\left(\frac{\partial \rho}{\partial T}\right)_{P}\mathrm{d}T = \mathrm{d}\rho - \frac{\gamma}{c^{2}}\mathrm{d}p} $$

将各级结论联立, 即有

$$ \frac{\partial p}{\partial t} - c^{2}\frac{\partial \rho}{\partial t} = \frac{\chi}{\rho_{0}C_{V}}\left(\frac{\partial^{2}p}{\partial x^{2}} - \frac{c^{2}}{\gamma}\frac{\partial^{2}p}{\partial x^{2}}\right) $$

• 运动方程 $$ \rho_{0}\frac{\partial^{2}\xi}{\partial t^{2}} = -\frac{\partial p}{\partial x} $$
• 连续性方程两边同时对 $x$ 求偏导 $$ \frac{\partial \rho}{\partial x} = -\rho_{0}\frac{\partial^{2}\xi}{\partial x^{2}} $$

代入以上两独立关系, 即得热传导效应下的声波方程:

$$ \frac{\partial^{2}\xi}{\partial t^{2}} = c^{2}\frac{\partial^{2}\xi}{\partial x^{2}} + \frac{\chi}{\rho_{0}C_{V}}\cdot\frac{\gamma - 1}{\gamma}\cdot\frac{\partial^{3}\xi}{\partial x^{2}\partial t} $$

类比于黏性吸收得声波方程, 替换系数得到热传导吸收系数为

$$ \alpha_{h} = \frac{\omega^{2}}{2\rho_{0}c^{3}}\frac{\chi(\gamma - 1)}{C_{V}\gamma} $$

$\gamma = \frac{C_{P}}{C_{V}}$. $c$ 为理想流体小振幅绝热波速.

对于水 $\gamma\approx 1$, 因此 $\alpha_{h}\ll \alpha_{\eta}$; 而对空气而言, $\gamma\approx 1.4$, $\alpha_{h}/\alpha_{\eta} \approx 3/8$. 因此气体得热传导吸收和切边黏性吸收为同等数量级.

声波吸收经典公式

将黏性和热传导效应线性叠加, 即得到 Stokes-Kirchhoff 公式:

$$ \alpha = \alpha_{\eta} + \alpha_{h} = \frac{\color{red}{\omega^{2}}}{2\rho_{0}c^{3}}\left[\frac{4}{3}\eta^{\prime} + \chi\left(\frac{1}{C_{V}} - \frac{1}{C_{P}}\right)\right] $$

这就是超声波极易衰减的原因.

注意: 该公式实际上并不能良好吻合, 因为忽略了容变黏度 $\eta^{\prime\prime}$.

分子弛豫吸收

为了解释和经典吸收值的偏离, 将分子内部自由度也考虑在内, 即状态变化考虑为内外自由度能量的重新分配, 这种平衡态的转移过程被称为弛豫. 标记一有限时间 $\tau$ 为弛豫时间; 声振动转变为热运动的能量耗散(区别于热传导)引起声波的附加吸收. 该过程在宏观上与容变黏度 $\eta^{\prime\prime}$ 有关.

---

设非平衡态的定容热容

$$ C_{V} = C_{V\infty} + C_{t}(1 - e^{-\frac{t}{\tau_{m}}}) $$

$C_{V\infty}$ 是外自由度贡献的热容量, 与弛豫无关; $C_{t}$ 是 $\tau_{m}\rightarrow 0$ 时内自由度可贡献的热容量; $\tau_{m}$ 是弛豫时间.

• 低频时, 周期 $1/f\gg\tau_{m}$, 即内外自由度随时保持平衡, 即有近似

$$ C_{t} = C_{V0} = C_{C\infty} + C_{t} $$

非线性声学

有限振幅声波不可用线性声学理论解释.

1. 单频声波产生谐波, 分频波, 和频波, 差频波. 波的叠加原理不成立;
2. 声速与流体应力呈正相关, 波形变为锯齿形;
3. 高次谐波频率高, 吸收衰减快…

非线性传播

设质点振速为

$$ u(x,t) = u_{m}\sin{(\omega t-kx)} $$

则有

$$ \left|u\frac{\partial u}{\partial x}\right|\propto ku_{m}^{2} = \frac{\omega}{c}u_{m}^{2},\quad \left|\frac{\partial u}{\partial t}\right|\propto \omega u_{m} $$

注意到两者之比为

$$ \frac{\left|u\frac{\partial u}{\partial x}\right|}{\left|\frac{\partial u}{\partial t}\right|} = \frac{u_{m}}{c} $$

可见, 该数值越大, 非线性项越不可忽略. 历史上将该参数称为 声马赫数.

---

参考流体力学中的基本方程, 建立非线性声学的基本关系:

$$ \frac{\partial\rho}{\partial t} + \nabla\cdot(\rho\mathbf{u}) = 0\\ \frac{\partial}{\partial t}(\rho\mathbf{u}) + \rho\mathbf{u}(\nabla\cdot\mathbf{u}) + (\mathbf{u}\cdot\nabla)\rho\mathbf{u} + \nabla p = 0\\ P = P_{0} + \left(\frac{\partial P}{\partial\rho}\right)_{\rho_{0}, S}(\rho - \rho_{0}) + \frac{1}{2!}\left(\frac{\partial^{2}P}{\partial\rho^{2}}\right)_{\rho_{0},S}(\rho - \rho_{0})^{2} + \dots $$

$\rho = \rho_{0} + \rho^{\prime}$ 为介质密度, $\rho_{0}$ 为静态平衡密度, $\rho^{\prime}$ 为 逾量密度(即声波引起的变化量); $S$ 为熵, $\left(\frac{\partial^{n}}{\partial \rho^{n}}\right)_{\rho_{0},S}$ 即等熵过程中 $P$ 对 $\rho$ 的 $n$ 阶导数.

线性声学中, 只取了一阶导数:

$$ P\approx P_{0} + \left(\frac{\partial P}{\partial \rho}\right)_{\rho_{0},S}\cdot(\rho - \rho_{0})\approx P_{0} + \rho_{0}\left(\frac{\partial P}{\partial \rho}\right)_{\rho_{0},S}\left(\frac{\rho - \rho_{0}}{\rho_{0}}\right)\approx P_{0} + A\frac{\rho - \rho_{0}}{\rho_{0}} $$

$$ A = \rho_{0}\left(\frac{\partial P}{\partial \rho}\right)_{\rho_{0},S} = \rho_{0}c_{0}^{2},\quad c_{0}^{2} = \left(\frac{\partial P}{\partial \rho}\right)_{\rho_{0},S} $$

$c_{0}$ 为小振幅波速.

对于有限振幅波, 则需要保留二阶小量:

$$ P\approx P_{0} + A\frac{\rho - \rho_{0}}{\rho_{0}} + \frac{B}{2}(\frac{\rho - \rho_{0}}{\rho_{0}})^{2} $$

$$ B = \rho_{0}^{2}\left(\frac{\partial^{2}P}{\partial \rho^{2}}\right)_{P_{0}, S}, \text{ or} B = \rho_{0}^{2}\left(\frac{\partial c^{2}}{\partial \rho}\right) $$

定义介质的 非线性参量 为

$$ \frac{B}{A} = \frac{\rho_{0}}{c_{0}^{2}}\left(\frac{\partial^{2}P}{\partial\rho^{2}}\right)_{P_{0},S} $$

---

对于理想气体绝热过程, 有

$$ \frac{P}{P_{0}} = \left(\frac{\rho}{\rho_{0}}\right)^{\gamma} $$

$\gamma = \frac{C_{P}}{C_{V}}$ 为绝热系数.

将其展开至二阶:

$$ \frac{P}{P_{0}} = 1 + \gamma\frac{\rho - \rho_{0}}{\rho_{0}} + \frac{1}{2}\gamma(\gamma-1)\left(\frac{\rho - \rho_{0}}{\rho_{0}}\right)^{2} $$

非线性参量为

$$ \frac{B}{A} = \gamma - 1 $$

---

对液体而言, 根据绝热体弹性模量 $K_{S}$ 的实验关系有经验公式

$$ K_{S} = \frac{\Delta P}{\left(\frac{\Delta\rho}{\rho}\right)_{S}} = n[P - B(S)] $$

$P$ 为外压力; $B(S)$ 为介质内分子压力, 是温度的函数; $n$ 是与液体有关的常数.

令 $P\rightarrow 0$, 则小振幅声速 $c_{0}^{2} = K_{S0}/\rho_{0}$, 所以有

$$ B(S) = \frac{\rho_{0}c_{0}^{2}}{n}\Rightarrow \frac{\mathrm{d}\rho}{\rho} = \frac{\Delta P}{n\left[P - \frac{\rho_{0}c_{0}^{2}}{n}\right]} $$

积分, 并且考虑到 $P\rightarrow 0$ 时 $\rho\rightarrow \rho_{0}$, 则有

$$ p = \frac{\rho_{0}c_{0}^{2}}{n}\left[\left(\frac{\rho}{\rho_{0}}\right)^{n} - 1\right] $$

展开至二阶, 整理出 $A$, $B$:

$$ A = \rho_{0}\left(\frac{\partial p}{\partial\rho}\right)_{P_{0},S} = \rho_{0}\frac{\rho c_{0}}{n} n \frac{\rho^{n-1}}{\rho_{0}^{n}}|_{\rho = \rho_{0}} = \rho_{0}c_{0}^{2}\\ B = \rho_{0}^{2}\left(\frac{\partial^{2}p}{\partial\rho^{2}}\right)_{P_{0}, S} = \rho_{0}^{2}\frac{\rho_{0}c_{0}^{2}}{n}\frac{n(n-1)\rho^{n-2}}{\rho_{0}^{2}}|_{\rho = \rho_{0}} = (n-1)\rho_{0}c_{0}^{2} $$

所以液体非线性参量的 经验公式 为

$$ \frac{B}{A} = n - 1 $$

---

理想介质中, 小振幅波列上任意一点速度相等, 而有限振幅波则并非如此.

考虑有限振幅的平面波在无黏理想流体中的一维传播情形:

$$ \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + \frac{1}{\rho}\frac{\partial p}{\partial x} = 0\\ \frac{\partial \rho}{\partial t} + \rho\frac{\partial u}{\partial x} + u\frac{\partial\rho}{\partial x} = 0\\ \frac{\mathrm{d}p}{\mathrm{d}\rho} = [c(\rho)]^{2} $$

理想介质中的绝热过程, 有事实: 质点速度 $u$ 和声速 $c$ 为密度 $\rho$ 的函数.

$$ u = u(\rho),\quad c = c(\rho) \Rightarrow \rho = \rho(u) $$

将上式与状态方程分别代入连续性方程和运动方程, 即有

$$ \left(\frac{\partial u}{\partial t}\right)_{x} + \left[u + \frac{c^{2}}{\rho}\frac{\mathrm{d}\rho}{\mathrm{d}u}\right]\left(\frac{\partial u}{\partial x}\right)_{t} = 0\\ \left(\frac{\partial \rho}{\partial t}\right)_{x} + \left[u + \rho\frac{\mathrm{d}u}{\mathrm{d}\rho}\right]\left(\frac{\partial \rho}{\partial x}\right)_{t} = 0 $$

变式化简:

$$ \frac{-\left(\frac{\partial u}{\partial t}\right)_{x}}{\left(\frac{\partial u}{\partial x}\right)_{t}} = u + \color{red}{\frac{c^{2}}{\rho}\frac{\mathrm{d}\rho}{\mathrm{d}u}}(*)\\ \frac{-\left(\frac{\partial \rho}{\partial t}\right)_{x}}{\left(\frac{\partial \rho}{\partial x}\right)_{t}} = u + \color{red}{\rho\frac{\mathrm{d}u}{\mathrm{d}\rho}}(*) $$

已知 $u(x,t)$ 全微分为

$$ \mathrm{d}u = \left(\frac{\partial u}{\partial x}\right)_{t}\mathrm{d}x + \left(\frac{\partial u}{\partial t}\right)_{x}\mathrm{d}t $$

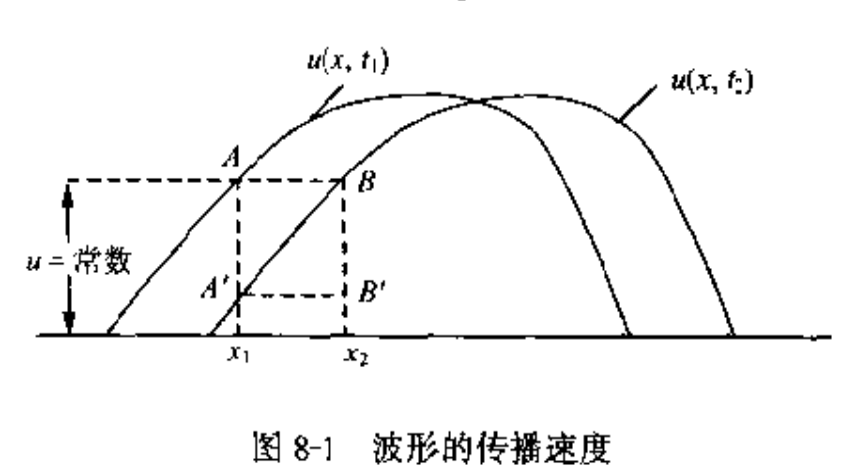
观察波形图像, 即有

$$ \mathrm{d}u = \left(\frac{\partial u}{\partial x}\right)_{t_{2}}(x_{2} - x_{1}) + \left(\frac{\partial u}{\partial t}\right)_{x_{1}}(t_{2} - t_{1}) = 0 $$

表示 $(x_{1},t_{1})\rightarrow (x_{2}, t_{2})$, 其中 $u = \textit{const.}$

所以信号传播速度定义为

$$ \left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)_{u} = \left(\frac{x_{2} - x_{1}}{t_{2} - t_{1}}\right) = \frac{-\left(\frac{\partial u}{\partial t}\right)_{x}}{\left(\frac{\partial u}{\partial x}\right)_{t}} $$

因为 $\rho$ 是 $u$ 的单值函数, 所以两者信号速度相同. 即有

$$ \color{red}{\frac{c^{2}}{\rho}\cdot\frac{\mathrm{d}\rho}{\mathrm{d}u} = \rho\frac{\mathrm{d}u}{\mathrm{d}\rho}}(*) \Rightarrow \left(\frac{\mathrm{d}u}{\mathrm{d}\rho}\right)^{2} = \left(\frac{c}{\rho}\right)^{2} \Rightarrow \frac{\mathrm{d}u}{\mathrm{d}\rho} = \pm\frac{c}{\rho} $$

$$ c^{2} = \left(\frac{\mathrm{d}p}{\mathrm{d}\rho}\right)_{S,\rho_{0}} $$

分离变量并积分, 得到

$$ u = \pm\int\frac{c}{\rho}\mathrm{d}\rho = \pm\int\frac{\mathrm{d}p}{\rho c} $$

将 $(**)$ 代入 $(*)$ 即得到信号传播速度

$$ \left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)_{u} = \left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)_{\rho} = u\pm c $$

积分得到

$$ x = (u \pm c)t + f(u) $$

$f(u)$ 是 $u$ 的任意函数. 正负表示沿 $x$ 轴正/负方向传播.

这就是非线性流体力学方程的一般解/Riemann 解. 写作隐函数形式:

$$ u = F[x - (u\pm c)t] $$

---

非线性畸变

液体的非线性参量

$$ \frac{B}{A} = n - 1 $$

根据上式写出声速方程

$$ c^{2} = \frac{\mathrm{d}p}{\mathrm{d}\rho} = \left(\frac{\rho}{\rho_{0}}\right)^{n-1}c_{0}^{2}\Rightarrow \boxed{c(\rho) = c_{0}\left(\frac{\rho}{\rho_{0}}\right)^{\frac{n-1}{2}}} $$

$$ \frac{\mathrm{d}u}{\mathrm{d}\rho} = \pm\frac{c}{\rho} $$

将声速方程代入, 并设定初始条件 $\rho = \rho_{0}, u = 0$, 解出

$$ u = \pm\int_{\rho_{0}}^{\rho}\frac{c(\rho)}{\rho}\mathrm{d}\rho = \pm\frac{2c_{0}}{n - 1}\left[\left(\frac{\rho}{\rho_{0}}\right)^{\frac{n-1}{2}}\right]\bigg{|}_{\rho_{0}}^{\rho} = \pm\frac{2c_{0}}{n-1}\left[\left(\frac{\rho}{\rho_{0}}\right)^{\frac{n-1}{2}} - 1\right]\\ = \pm\frac{2}{n-1}(c - c_{0}) $$

整理变式, 有

$$ c = c_{0} \pm\frac{n - 1}{2}u $$

当质点速度 $u$ 与声速相比不可忽略时, 不同点的声速 $c$ 将不同.

将上式代入隐函数中:

$$ u(x, t) = F\left[x - \left(\frac{n + 1}{2}u \pm c_{0}\right)t\right] $$

考虑 $x^{+}$ 波, 则波速为

$$ \left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)_{u} = c_{0} + \frac{n + 1}{2} u = c_{0} + \color{red}{\left(1 + \frac{B}{2A}\right)}u = c_{0} + \color{red}{\beta} u $$

---

声源产生正弦振动 $u = u_{m}\sin{\omega t}$. 根据上式, 有

$$ u = u_{m}\sin{\left(\omega t - \frac{\omega x}{c + u}\right)} = u_{m}\sin{\left(\omega t - \frac{\omega x}{c_{0} + \frac{n + 1}{2}u}\right)} $$

波列上各点移速不同, 波形在传播过程中发生变形.

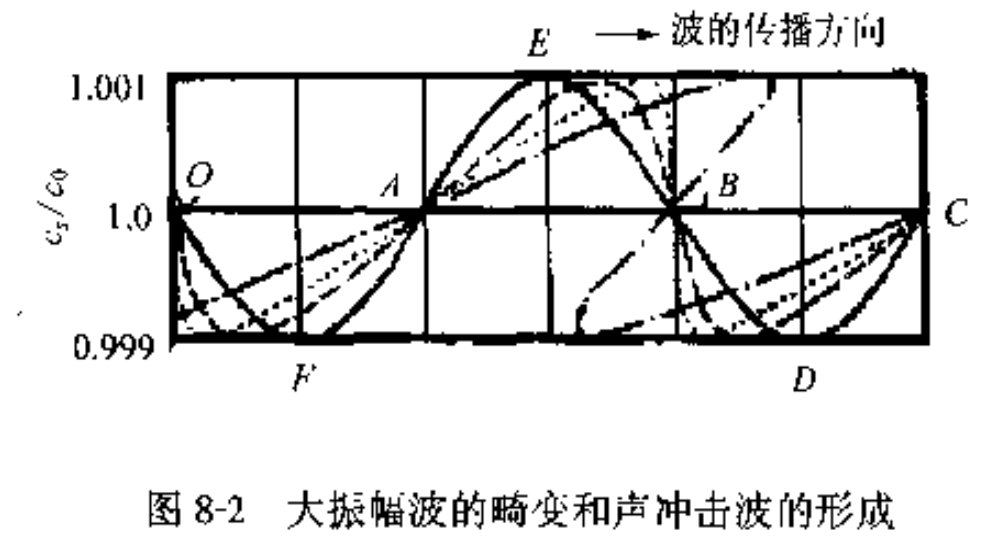
波的传播会使得波形趋近于锯齿波, 原本的等熵/绝热近似失效, 产生波的间断. 定义间断为

$$ \frac{\partial u}{\partial x} = \infty, \quad\text{or } \frac{\partial x}{\partial u} = 0 $$

对隐函数求导, 解得发生间断的临界距离

$$ x_{h} = \frac{\lambda c_{0}}{\pi(n + 1)u_{m}} = \frac{2\rho_{0}c_{0}^{3}}{(n + 1)\omega p_{m}} = \frac{\lambda}{\pi(n + 1)\text{Ma}} $$

初始正弦波的声压振幅/振速越大, 则在越短的距离上形成锯齿波. 畸变效应是会随着距离积累的, 即使初始振幅并不大.

---

将 $\omega$ 的正弦波在传播中的畸变理解为产生高次($2\omega, 3\omega,\dots$) 谐波的过程.

设声源 $u = u_{m}\sin{\omega t}$. 已知振速波函数为

$$ u(x , t) = u_{m}\sin{\omega\left[t - \frac{x}{c_{0} + \left(1 + \frac{B}{2A}\right)u(x, t)}\right]} $$

取小振速近似 $|u|/c_{0}\ll 1$, 有

$$ \frac{1}{c_{0} + \left(1 + \frac{B}{2A}\right)u(x, t)} = \frac{1}{c_{0}}\left[1 + \beta\frac{u}{u_{0}}\right]^{-1}\approx \frac{1}{c_{0}}\left[1 - \beta\frac{u}{c_{0}}\right] $$

就有

$$ u(x, t) = u_{m}\sin{\left[\left(\omega t - \frac{\omega}{c_{0}}x\right) + \beta\frac{\omega x}{c_{0}^{2}}u\right]} $$

以和角公式展开, 且取 $\beta\ll 1$, 有 $\sin{\epsilon} = \epsilon, \cos{\epsilon} = 1$ 极限:

$$ u(x, t)\approx u_{m}\sin{\omega t - k_{0} x} + u_{m}\frac{\beta\omega x}{c_{0}^{2}}\cos{(\omega t - k_{0}x)}\cdot u(x, t)\\ \Rightarrow u(x, t) \approx u_{m}\sin{(\omega t - k_{0}x)}\cdot\left[1 - \frac{\beta\omega x}{c_{0}^{2}}u_{m}\cdot\cos{(\omega t - k_{0}x)}\right]^{-1} $$

展开:

$$ u(x, t)\approx u_{m}\sin{(\omega t - k_{0}x)} + \frac{\beta \omega x}{2}\left(\frac{u_{m}}{c_{0}}\right)^{2}\sin{[2(\omega t - k_{0}x)]} + \dots $$

所以二次谐波振幅为

$$ u_{2\omega} = \left(\frac{n + 1}{4}\right)\left(\frac{u_{1\omega}}{c_{0}}\right)^{2}\omega x\quad(u_{1\omega = u_{m}}) $$

声压为

$$ p_{2\omega} = \frac{n + 1}{4}\left(\frac{u_{1\omega}}{c_{0}}\right)^{2}\omega x\rho_{0}c_{0} = \frac{(n + 1)\omega x}{4\rho_{0}c_{0}^{3}}p_{1\omega}^{2} $$

非线性吸收

不存在弛豫过程时, 吸收主要由介质黏性引起. 高次谐波更容易被吸收, 因此有限振幅声波的能量吸收率比小振幅声波的大.

定义声 Reynolds 数

$$ \text{Re} = \frac{p}{b\omega} $$

$p$: 声压; $\omega = 2\pi f$: 声波角频率; $b = \frac{4}{3}\eta^{\prime} + \eta^{\prime\prime}$, $\eta^{\prime}$: 切变黏度; $\eta^{\prime\prime}$: 容变黏度.

• $\text{Re}\gg 1$.

声波强, 黏性小. 非线性效应很强. 在介质中形成稳定的锯齿波传播, 能量损失很大, 介质吸收强;

• $\text{Re}\ll 1$.

基波能量持续交换至高次谐波, 但高次谐波能量很快被介质吸收, 使得波形存在一段稳定区, 不致形成锯齿波, 但是仍比小振幅波的吸收强.

---

在黏性介质中主要考虑基波与二次谐波. 代入黏性解出的声压表达式为

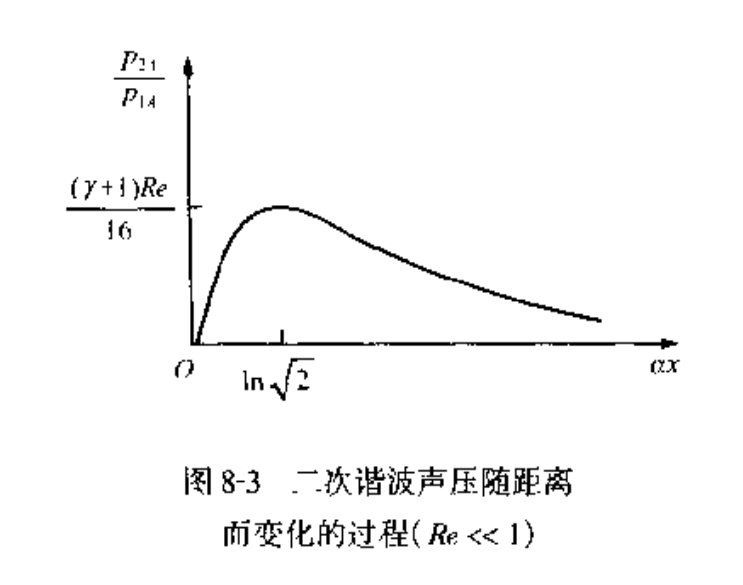
$$ p_{1\omega} = p_{m}e^{-\alpha x}\sin{\omega\left(t - \frac{x}{c_{0}}\right)}\\ p_{2\omega} = \frac{(n + 1)p_{m}^{2}}{4b\omega}(e^{-2\alpha x} - e^{-4\alpha x}) \sin{2\omega\left(t - \frac{x}{c_{0}}\right)} $$

$$ \alpha = \frac{\omega^{2}}{2\rho_{0}c_{0}^{2}}\left(\frac{4}{3}\eta^{\prime} + \eta^{\prime\prime}\right) $$

对于有限振幅声波, 其声压并不随距离呈现指数衰减, 吸收常数也并非定值.