通用声学方法
-
声速测量. 推算介质的密度, 弹性模量等信息;
-
声衰减测量. 推断介质的吸收性质, 从而得到介质的黏度等信息;
-
超声多普勒成像. 通过多普勒频移计算流体的流速;
-
声波谱分析, 分析声波的频谱得知介质中不同频率成分的响应;
-
声波散射. 介质中的异质性(颗粒, 气泡)产生散射, 测量散射特性即可推算颗粒的大小形状等.
周志刚
装置设计
超声仪器
真空泵. 1. 制备样品时使得橡皮膜和固定模具贴合; 2. 给颗粒样品抽真空;
如此一来, 干燥的定义就需要重新理解了.
目前的探头更多的是产生压缩波, 周的论文中存在着在样品中产生剪切波的探头.
当要产生压缩波时,ULT-100 的控制开关是调到压缩波晶体的,此时剪切波晶体不会被ULT-100 的电压信号激励。压缩波是压头表面上下振动产生,而剪切波是由与剪切波晶体相连的弯曲元左右振动产生的。…因此, P 波需要定标时间, 而 S 波不需要.
虽然压电晶体的中心频率为 $80\text{ kHz}$,但在制作压头时,压电晶体和其表面上包覆的金属保护层的耦合情况不同,使得从压头发出的波是由很多不同的频率成分组成的,如图 4.6 是频率谱,并且这随着压头的制作工艺情况会有所不同。
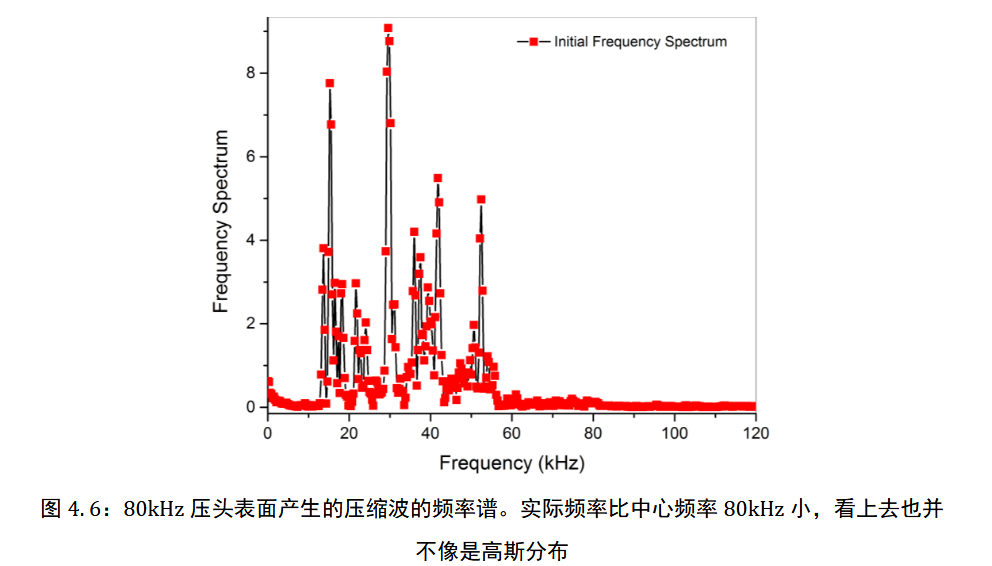
这样的探头显然是无法做到类似于 Jia 所称的 “以 $500\text{ kHz}$ 为中心的宽带频谱” 的. 我们目前的探头也是以 $129.2\text{ kHz}$ 为共振频率的探头, 它真的能承担起对应的功能吗?
周的飞行时间确定是第一个明显波峰的 $3$%, 而不是之前我的模仿实验的波前. 此处周并未考虑有关于飞行时间参考点选取的问题, 是避重就轻还是无意为之?
第一性原理
固体中声波传播和固体的模量紧密相关. 一般声速和模量的关系:
$$ V_{p} = \sqrt{\frac{K+4\mu/3}{\rho^{*}}}\\ V_{S} = \sqrt{\frac{\mu}{\rho^{*}}} $$
$\rho^{*}$: 颗粒固体样品的密度; $K$: 体变模量; $\mu$: 剪切模量
$$ K = \frac{C_{n}}{12\pi}(\phi z)^{\frac{2}{3}}\left(\frac{6\pi P}{C_{n}}\right)^{\frac{1}{3}}\\ \mu = \frac{C_{n} + \frac{3}{2}C_{t}}{20\pi}(\phi z)^{\frac{2}{3}}\left(\frac{6\pi P}{C_{n}}\right)^{\frac{1}{3}} $$
$\phi = \rho^{*}/\rho$, $\rho$ 为颗粒材质密度, $\phi$ 为颗粒体系的体积分数, $Z$ 为平均配位数, $C_{n}, C_{t}$ 分别为颗粒在法向和切向的系数.
EMT 处理的前提条件: 声波波长 $\gg$ 颗粒直径, 颗粒体系中的颗粒相同, 满足紧束缚条件, 颗粒体系的应变满足仿射近似. 严格意义上的 EMT 紧束缚条件是不成立的, 应当采用修正:
$$ Z = Z_{c} + \left(\frac{P}{1\text{ MPa}}\right)^{\frac{1}{3}},\quad\phi = \phi_{c} + \left(\frac{P}{14\text{ GPa}}\right)^{\frac{2}{3}} $$
周志刚的采用值为 $Z_{c} = 5.5, \phi_{c} = 0.61$.
$\rho$: 密度
$\rho v_{i}$: 动量
$u_{ij}$: 弹性应变
$S$: 热力学熵
$S_{g}$: 颗粒熵
$$ \partial_{t}(\rho v_{i}) + \nabla_{j}(\sigma_{ij} + \rho v_{i}v_{j}) = 0\\ \partial_{t}u_{ij} - (1 - \alpha)v_{ij} + \frac{u_{ij}^{0}}{\tau} + \frac{u_{ll}\delta_{ij}}{\tau_{1}} = 0 $$
颗粒体系所受的力 $\sigma_{ij} = (1 - \alpha)\pi_{ij} - \zeta_{g}v_{ll}\delta_{ij} - \eta_{g}v_{ij}^{0}$, 其中 $\pi_{ij} = -\partial w/\partial u_{ij}$, $w$ 为弹性能, $\eta_{g}, \zeta_{g}$ 与粘滞相关, 且为颗粒温度 $T_{g}$ 的函数($T_{g}\rightarrow 0$ 时, 这些系数也为 $0$).
声波振动幅度极小而不引起体系结构的较大变化($T_{g} = 0$), 此时有 $\alpha, \tau_{1}, \tau_{1}^{-1}, \eta_{g}, \zeta_{g} = 0$. 采取条件 $u_{ij} = \frac{1}{2}(\partial_{i}U_{j} + \partial_{j}U_{i})$:
$$ \rho\ddot{U}_{i} + M_{ijkl}\nabla_{jk}U_{l} = 0 $$
颗粒固体的刚度张量 $M_{ijkl} = \partial^{2}\omega/\partial u_{ij}\partial u_{kl}$, 其中弹性能表达式为
$$ w = \mathcal{B}\sqrt{\Delta}\left(\frac{2\Delta^{2}}{5} + \frac{u_{S}^{2}}{\xi}\right) $$
$\Delta = -u_{ll}$: 颗粒样品应力主轴上的应变量. $u_S^{2} = u_{ij}^{0}u_{ij}^{0}$, $u_{ij}^{0} = u_{ij} + \delta_{ij}\Delta/3$, $\mathcal{B} = \mathcal{B}_{0}\left(\frac{\phi - \phi_{\text{lp}}^{*}}{\phi_{\text{cp}} - \phi}\right)^{\frac{3}{20}}$, $\phi_{\text{cp}}$ 和 $\phi_{\text{lp}}$ 为最密/松堆积时的体积分数. 存在关系 $\phi_{\text{lp}} = (11\phi_{\text{cp}} + 9\phi_{\text{lp}}^{*})/20$
颗粒介质在主轴方向受压力 $P = \pi_{ll}/3$, 剪切力 $\pi_{S}^{2} = \pi_{ij}^{0}\pi_{ij}^{0}$. 弹性应变:
$$ u_{ij}^{0} = -\frac{\pi_{ij}^{0}}{2\mu} $$
$\mu = \frac{\mathcal{B}}{\xi}\left(\frac{LP}{\mathcal{B}}\right)^{\frac{1}{3}}, 2L = 1 + \sqrt{1 - \xi\pi_{S}^{2}/(2P^{2})}, \Delta = \left(\frac{LP}{\mathcal{B}}\right)^{\frac{2}{3}}, u_{S} = \pi_{S}/(2\mu)$.
颗粒体系中应力与应变均匀的情况下, 刚度张量有
$$ M_{ijkl} = \mu(a_{(ik)}\delta_{ij}\delta_{kl} - \delta_{ik}\delta_{jl} - \delta_{il}\delta_{jk}) $$
$a_{(ik)} = \left(\frac{\xi\pi_{S}^{2}}{4LP}\right)^{2} + \frac{4-9\xi}{6} - \frac{\xi(\pi_{i}^{0} + \pi_{k}^{0})}{2LP}$
设波动方程的解极限形式为平面波~ $e^{\omega t + \vec{\mathbf{k}}\cdot\vec{\mathbf{x}}}$, 化为特征方程
$$ (K_{il} - \lambda\delta_{il})U_{l} = 0 $$
$K_{il} = \frac{(\beta_{(i)} + \beta_{(l)})n_{i}n_{l}}{2}-\delta_{il}, n_{i} = k_{i}/k, \beta_{i} = 1 - Q - \frac{\xi\pi_{0}^{0}}{LP}, Q = \frac{3\xi}{2} + \frac{4}{3} - \frac{\xi\pi_{S}}{4LP}$
颗粒固体中超声波的传播. 无论是周志刚还是之前所阅读的贾小平的文章, 都是致密固体中的情形, 显然并不是太适用于所需要用到的动力学体系.
颗粒固体对声波的扰动会非常敏感, 不同能量的声波对颗粒固体体系的作用.
贾小平
暑校视频解读
- 在堵塞态的颗粒固体中的线性超声传播(探测)
利用声波来研究固液相变(Unjamming transition):
非破坏性的探测: $u_{\text{ac}} < 1\text{ nm}$; 受控诱导(Pump): $u_{\text{ac}}$~$0.01-10\mu\text{m}$. $u_{\text{ac}} < d$ 意味着 $f_{\text{ac}} = 0.1-100\text{ kHz}$
声音在颗粒介质中的传播: 无序 & 非线性
发射信号: (1) 高幅值, 连续波 $\rightarrow$ 强烈的强度涨落; (2)低幅值, 脉冲波 $\rightarrow$ 有效介质的失效(具体体现在 $V_{\text{tof}}\neq V_{g}$).
e.g. 发射单周期的周期为 $f_{c}$ 的正弦信号, 在经过了厚度为 $L$ 的颗粒介质, 假设可以控制边界条件 $\partial V$, 接收信号为 $A(t)$ 的强度曲线, 如何分析出群速度 $V_{g}$, 群速度能够反映出颗粒介质怎样的特征?
设平面波速率 $v$ 为波长 $\lambda$ 的函数 $v = v(\lambda)$, 则波速, 波长, 频率 $f$ 存在关系:
$$ v(\lambda) = \lambda f(\lambda) $$
用角频率 $\omega = 2\pi f$ 和波数 $k = \frac{2\pi}{\lambda}$ 改写则为
$$ \omega(k) = v(k)k $$
则有相速度 $v_{\phi} = \frac{\omega}{k}$ 和群速度 $v_{g} = \frac{\partial\omega}{\partial k}$
如果将信号写作
$$ u(x,t) = Ae^{i(\omega t - kx)} = Ae^{i\varphi(x,t)} $$
示例实验参数
$P = 3-3000\text{ kPa}, d = 0.1-10\text{ mm}, D = 30\text{ mm}$. 单周期或多周期的正弦信号.
$\lambda\geq 10d$: 相干波(E), 呈现低通特性, 可复现; $\lambda_{S}\approx 2d$: 多次散射波(S), 呈现广谱特性, 结构敏感.
-
相干波波速和压力的关系: $V_{L,T}(P)\propto [Z(P)]^{\frac{1}{3}}\cdot[k(P)]^{\frac{1}{2}}\propto P^{\frac{1}{6}}$, $Z$ 为配位数.
-
相干波波速和颗粒形状的关系: 颗粒形状影响接触数, 从而影响波速.
弹性的各向异性: 应力场的各向异性和结构(Elastic anisotropy: stress-field anisotropy and fabric). 压缩波只对应力各向异性敏感, 而剪切波对结构的各向异性也非常敏感.
声波速度(压缩波 $V_{P}$)在颗粒层中的涨落.
在颗粒介质中剪切波的多重散射.
我们的探头可以探测到剪切波吗? 如果能, 如何将其在信号 $A(t)$ 中寻找出来? 我怀疑我们并没有一个剪切传感器(shear transducer). 将探头摆在侧壁可以起到测量横波的作用吗?(这就是论文中提到的 $2\text{ mm}$ 探头的作用? 因此也是越小越好吗?)
$$ \partial_{t} I - D\nabla^{2}I + \frac{I}{\tau_{a}} = \delta(z)\delta(t) $$
$D = \frac{1}{3}v_{e}l^{*}$ 扩散系数(the diffusion coefficient), $\tau_{a}$ 为非弹性吸收时间(the inelastic absorption time)
设定圆筒壁和 $z = L$ 均为完全反射的边界条件, 则进入探测器的透射通量 $J(t) = (v/4)U(L,t)$:
$$ J(t) = \frac{\nu U_{0}}{2L}e^{-\frac{t}{\tau_{a}}}\sum_{n=0}^{\infty}\frac{(-1)^{n}}{\delta_{n}}\cos{\left(\frac{n\pi l^{*}}{L}\right)}e^{-\frac{D(n\pi)^{2}t}{L^{2}}} $$
$U_{0}$ 是沉积源能量, $D = (1/3)v_{e}l^{*}$ 是扩散系数, $v_{e}$ 是能量传输速度, $l^{*}$ 是传输平均自由程, $\tau_{a}$ 是非弹性吸收时间, 当 $n = 0$ 时, $\delta_{n} = 2$, 否则, $\delta_{n} = 1$.
如何绘制出信号的强度-时间曲线? 换言之, 如何根据 $A(t)$ 计算出强度 $I$?
传输平均自由程 $l^{*}$ 和应力 $P$ 的演化关系. 在低应力的情况下, 扩散模型或将失效?
使用波长 $\lambda$ 标定传输自由程 $l^{*}$. 借用瑞利散射的概念: 传输自由程 $l^{*}$ 和波长 $\lambda$ 的关系. 即散射粒子尺度由于远小于波长, 从而有散射量与波长的四次方成反比. 即 $I\propto\lambda^{-4}$.
通过数字滤波可以去除颗粒固体中的相对低频的相干波(压缩波P和剪切波S), 通过平方滤波波形的包络来测定散射波的强度. (即先滤波去除 $300\text{kHz}$, 然后对信号进行平方, 最后对得到的信号进行包络处理)
质量因子 $Q = 2\pi f\tau_{a}$, 其中 $\tau_{a}$ 需要通过扩散方程的理论曲线拟合得到.
用扩散散射波探测干湿颗粒介质的内部耗散(Probing the internal dissipation in dry and wet granular media with diffusively scattered waves). 液体所占体积分数极少, 只起到对接触面进行润滑的作用.
和月震曲线类似. 地震是快且短促的 P 波和一个慢且较宽的 S 波. 干颗粒介质则是通常意义上的颗粒响应曲线. 这启示月震原理可能可以用干颗粒介质来解释.
玻璃珠堆积中的界面耗散机制(Interfacial dissipation mechanisms in glass bead packings)
$$ Q^{-1}_{\text{fric}}\propto \mu^{-1} U_{t} P^{-\frac{2}{3}}\\ Q^{-1}_{\text{liq}}\propto \nu\delta_{\text{liq}}^{-1} P^{1/3} $$
$\nu$: 黏度; $\delta_{\text{liq}}$: 液膜厚度; $U_{t}$: 界面的相对速度; $\mu$: 库仑摩擦系数. 该实验中使用的是硅油进行润滑.
标志着局部摩擦的非线性, Mindlin 模型失效, 使用库仑摩擦 $\mu$ 来描述局部摩擦不再合理.
润滑玻璃珠堆积中的界面耗散. 粘性耗散主要发生在接触区的液膜中,但不发生在"半月板"中。
探测颗粒介质中的剪切带(Probing the shear-band formation in Granular Media). 剪切带表示颗粒介质从固-液相变.
传统方法: 光弹; X 辐照; 核磁共振断层扫描(MRI tomography). 但是对于实地实验应用困难.
剪切波宏观可以看弹性模量, 微观可以看颗粒的重排.
参数: 法向应力 $N = 330\text{ N}$, 剪切速度 $V = 0.6\mu\text{m/s}$ (准静态), 颗粒直径 $d = 700\pm 20\mu\text{m}$. 制备方法: 致密(雨落法), 松散(解压法).
力变曲线的测定, 以及剪胀性测定.
小振幅弹性波的传播(Small-amplitude elastic wave propagation). 发射长度 $4\mu\text{s}$ 正弦波脉冲.
等效介质近似 + 等静压近似, 有
$$ V_{S} = \sqrt{\frac{G}{\rho}}\propto z^{\frac{1}{3}}\cdot\phi^{-\frac{1}{6}}\cdot P^{\frac{1}{6}} $$
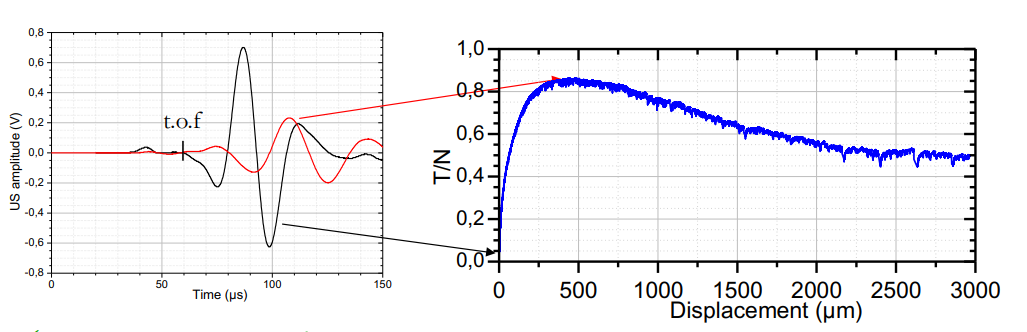
不同剪切条件下, 相同的试探信号产生的响应波形也不相同. 这说明, 剪切波的波速 $V_{S}$ 对颗粒介质的各向异性高度敏感.
不同初始堆积. 初始堆积下, 呈现剪切波速度-剪切应变曲线; 进行重复负载后, 剪切波在不同的剪切应变下的速度趋于定值. 初始堆积的力变曲线呈现屈服点而重复负载没有, 这可以说明剪切带只在初始堆积中存在而重复负载后消失了.
循环负载.
当系统探索不同的亚稳态构型时,S 波速的滞后行为 = 微观结构的演变
用散射尾波探测间歇动力学(Probing intermittent dynamics with scattered coda waves)
使用 $\Gamma_{ij}$ 描述声学信号 $S_{i}$ 和 $S_{j}$ 之间的关联性, 即将两者的时域信号进行卷积, 最大相关为 1, 完全无关为 0. 放大后可以观察到类似于 stick-slip 行为的骤降和缓升.
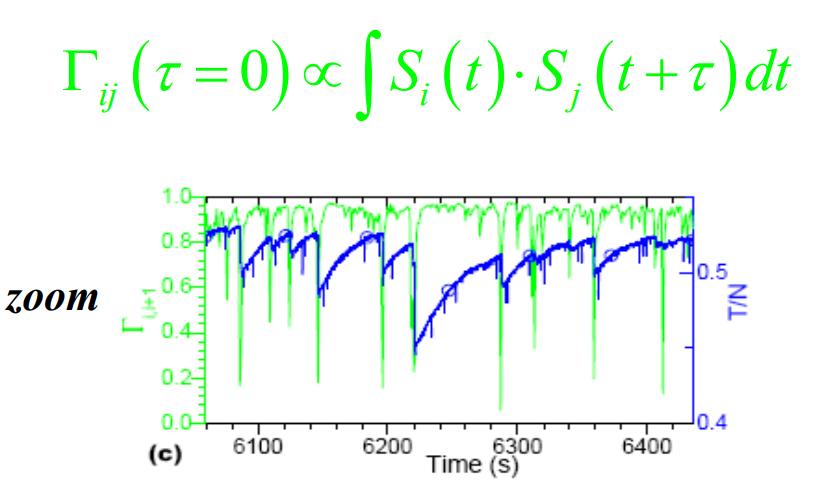
$$ \Gamma_{ij}(\tau = 0)\propto\int S_{i}(t)\cdot S_{j}(t + \tau)\mathrm{d}t $$
初始堆积(致密堆积和松散堆积)的力变曲线不同, 但是 $\Gamma_{i,i+1}$ 在应变范围内都保持高关联程度(~1).
不同尺度 ($\lambda_{E}/d$) 下的声学测量.
- $\lambda_{E}/d \geq 10$.
相干弹性波. 测量颗粒介质的体积模量 $K$ 和 剪切模量 $G$. 而 $K,G$ 对颗粒的
- 杨氏模量/弹性模量 $E$ (Young’s Modulus/Elastic Modulus): (正应力和正应变之间的线性表示)
$$ \sigma_{ii} = \color{red}{E}\epsilon_{ii} $$
类比于一维 Hooke 定律 $F = \color{red}{k}\Delta x$
- 剪切模量/剪切弹性模量/切变弹性模量 $G$ (Shear Modulus)
$$ G = \frac{\tau}{\gamma} $$
$\tau$ : 剪切应力($\text{MPa}$); $\gamma$: 剪切应变($\text{rad}$)
- 体积模量 $K$ (Bulk Modulus): 描述均质各向同性固体的弹性. 和弹性模量 $E$ 有直接关系式:
$$ K = \frac{E}{3\times(1-2\mu)} $$
$\mu$ 为泊松比, 定义为横向应变和轴向应变之比. 泊松比可以为负.
其物理意义为, 若物体在 $P_{0}$ 应力下体积为 $V_{0}$, 设应力增加为 $P_{0} + \mathrm{d}P$, 体积 减小 为 $V_{0} - \mathrm{d}V$, 则
$$ K = -\frac{\mathrm{d}P}{\mathrm{d}V/V_{0}} $$
- $\lambda_{E}/d$ ~ $1$.
测量 $Q$ 从而反映接触点的耗散;
计算平均自由程 $l^{*}$ 从而反映颗粒的重排.
- 超声波 界面流变
剪切谐振器和微珠层
- 在脆弱颗粒固体中的非线性超声传播(探测/诱导)
- 高振幅波的激励响应. 测量高次谐波振幅和非线性系数 $\beta$.
非线性机制: Hertz 非线性 + Mindlin 非线性
不同应变强度下的机制.
- 弱线性机制($\varepsilon_a \ll \epsilon_{0}$)
$\sigma_{a} = M_{0}\varepsilon_{a}(1 + \beta\varepsilon_{a} + \dots),\quad\beta = -\frac{1}{4\varepsilon_{0}}$
谐波产生. (这就是所谓的倍频效应)
-
- 摩擦耗散 Brunet, Jia, Mills, PRL 101 (2008)
-
- 剪切刚度变弱
-
强非线性机制($\varepsilon_a \gg \epsilon_{0}$)
冲击波
Coste, Falcon, Fauve (1997); Sen et al, 2008 Dario, Nesterenko et al (2006); Huillard, Noblin, Rajchenbach (2011) Gomez, Wildenberg, van Hecke, Vitelli (2011): 2D/3D disordered packs
十循环音爆激励, $f_{0} = 50\text{ kHz}$.
连续性方程
$$ \sigma_{a} = K_{0}\epsilon_{a}(1 + \beta\epsilon_{a} + \dots) + \eta\frac{\partial \epsilon_{a}}{\partial t},\quad \beta_{\text{Hertz}} = \frac{1}{4\epsilon_{0}} $$
声-弹 方程
$$ \beta_{AE} = \frac{\rho_{0}}{2}\left(\frac{\mathrm{d}c_{0}^{2}}{\mathrm{d}P_{0}}\right) $$
非线性波方程
$$ \mathbf{\rho}_{0}\frac{\partial^{2}u}{\partial t^{2}} - \mathbf{\eta}\frac{\partial^{3}u}{\partial a^{2}\partial t} - \mathbf{\rho}_{0}c_{0}^{2}\frac{\partial^{2}u}{\partial a^{2}} - 2\mathbf{\rho}_{0}c_{0}^{2}\mathbf{\beta}\left(\frac{\partial u}{\partial a}\right)\left(\frac{\partial^{2} u}{\partial a^{2}}\right) = 0 $$
在伯格斯方程的基础上添加了 $\eta$ 类比于黏度.
带黏度的小振幅波方程为
$$ \rho_{0}\frac{\partial^{2}\xi}{\partial t^{2}} - \rho_{0}c_{0}^{2}\frac{\partial^{2}\xi}{\partial x^{2}} - \eta\frac{\partial^{3}\xi}{\partial x^{2}\partial t} = 0 $$
Burgers 方程为
$$ \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} = \nu\frac{\partial^{2}u}{\partial x^{2}} $$
所以重点在于如何理解非线性波方程里的带 $\beta$ 的项. 我的初步理解:
$$ c = c_{0} + \beta \frac{\partial \xi}{\partial t} $$
将 $c\rightarrow c_{0}$, 忽略二阶小量, 即欲证明
$$ \rho_{0}(c_{0} + \beta \frac{\partial \xi}{\partial t})^{2} = 2\beta\rho_{0}c_{0}^{2}\frac{\partial \xi}{\partial t}\frac{\partial^{2} \xi}{\partial x^{2}}\Rightarrow \frac{\partial\xi}{\partial t} = c_{0} \frac{\partial \xi}{\partial x} $$
而信号速度的定义正是
$$ c_{0} = \frac{\frac{\partial\xi}{\partial t}}{\frac{\partial \xi}{\partial x}} $$
实际上是有一个负号的, 但是没有太懂这个负号为什么在这里消失了. 如果解释为 $c_{0} - \beta \frac{\partial \xi}{\partial t}$ 能好一些吗?
最后解出各个波的振幅函数.
$$ \begin{cases} u_{1\omega}(a,t) \approx u_{\text{in}}e^{-a\alpha}\cos{(ka-\omega t)}\\ \\ u_{2\omega}(a,t) \approx \frac{u_{\text{in}}^{2}}{8}\left(\frac{\beta\omega^{2}}{\alpha c_{0}^{2}}\right)e^{-2\alpha a}\cos{[2(ka-\omega t)]}\\ \\ u_{3\omega}(a,t) \approx \frac{u_{\text{in}}^{3}}{48}\left(\frac{\beta\omega^{2}}{\alpha c_{0}^{2}}\right)^{2}e^{-3\alpha a}\cos{[3(ka-\omega t)]} \end{cases} $$
压缩波波速软化.
颗粒固相中的非线性共振.
- 压缩模
Nonlinear dynamics, granular media and dynamic earthquake triggering
- 剪切模
Shear-wave-induced softening and simultaneous compaction in dense granular media through acoustic lubrication at flow heterogeneities
- DEM 模拟
Dynamic induced softening in frictional granular material investigated by DEM simulation
- 颗粒沉积物中的剪切波速度软化(Shear wave velocity softening in granular sediments)
Drastic slowdown of the Rayleigh-like wave in unjammed granular suspensions
表面振动波
类 Rayleigh 表面波
边界堵塞颗粒介质中的孤子/冲击(Solitons/Shocks in marginally jammed granular media)
Wildenberg, Yang and Jia (unpublished)
存在自由表面的颗粒堆积中的冲击波前的传播(Shocks front propagation in bead packings with free surface)
总结
-
通过接触滑动的剪切模量软化作用,声学流化可能会在堆积密度没有明显变化的情况下发生;
-
通过接触数 $Z$ 的损失,在颗粒材料的塑性变形和扩张过程中,可以观察到解堵塞转变阶段的强非线性弹性。
通过接触点的声学润滑诱发固体滑动和颗粒雪崩
- 通过声学流化引发颗粒介质中的剪切不稳定性(诱导)
(1) 地震触发/动力减弱
- Melosh, Nature 379 (1996)
- Johnson, Jia, Nature 437 (2005)
- Johnson, Gomberg, Marone et al, Nature 451 (2008)
- Probing the shear-band formation in granular media with sound waves
(2) 振动颗粒介质的雪崩/流变学
- Jaeger, Liu, Nagel, PRL 62 (1989)
- Dijksman, van Hecks et al, PRL 107 (2011)
- Triggering granular avalanches with ultrasound
(3) 滑动触发玻璃状界面
- Heuberger, Drummond, Israelachvili, J. Phys Chem. (1998)
- Bureau, Baumberger, Caroli, PRE 64 (2001)
- Léopoldès, Conrad, Jia, PRL 110 (2013)
剪切振荡引发的不稳定性
-
粗糙表面的滑坡
-
单点接触的滑动
声学流化引发的不稳定性:颗粒雪崩
Triggering granular avalanches with ultrasound
Ball sinking in vibrated dense granular suspensions:
振动致密颗粒悬浮液中的沉球:
-
垂直振动
-
水平振动
摩擦流变学 (GDR MIDI 2004; Courrech du Ponts et al, PRL 2003; Cassar et al, POF 2005)
存在解析解
涨落耗散定理 (颗粒介质)
沉降球调查与超声波成像相结合,为三维颗粒沉积物的局部流变学测量提供了一种便捷的方法
(Ultrasonic tracking of a sinking ball in a vibrated dense granular suspension)

