经典散射理论
Intro
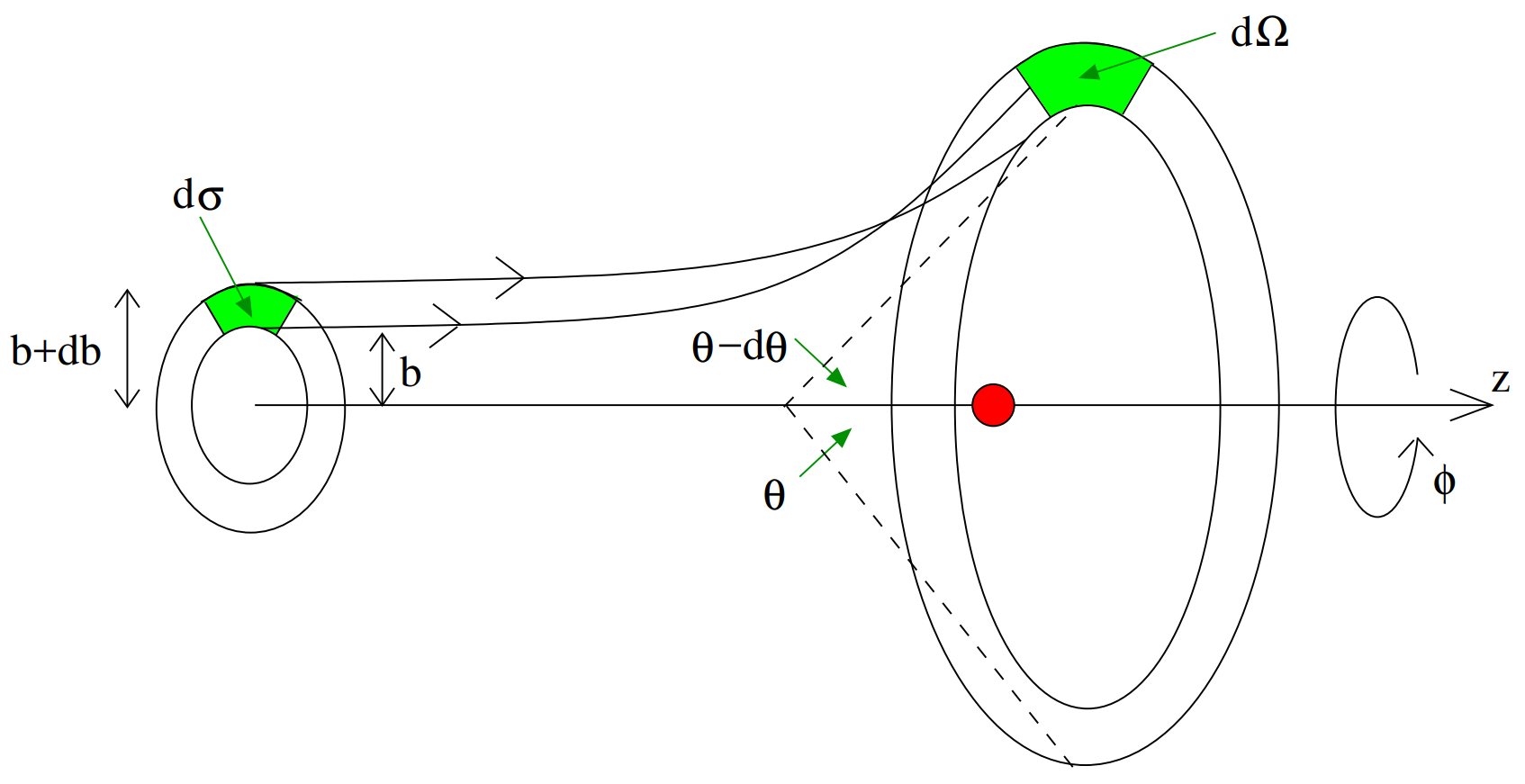
假设粒子从无穷远处入射, 方向为 $\hat{z}$, 动能为 $E$. $b$ 是粒子与 $z$ 轴的距离. 现在可以计算出射角度 $\theta$ 作为 $b$ 和 $E$ 的函数 $\theta(b,E)$.
假定入射粒子流的能量 $E$ 和碰撞系数 $b$ 均匀, 那么入射横截面 $\mathrm{d}\sigma$ 有
$$ \mathrm{d}\sigma = b\color{red}{\mathrm{d}\phi}\mathrm{d}b $$
立体角微分为
$$ \mathrm{d}\Omega = \sin{\theta}\mathrm{d}\theta\color{red}{\mathrm{d}\phi} $$
对公共部分进行替换联立:
$$ \frac{\mathrm{d}\sigma}{\mathrm{d}\Omega} = \frac{b}{\sin{\theta}}\left|\frac{\mathrm{d}b}{\mathrm{d}\theta}\right| $$
这就是 微分散射截面 的定义.
$\hat{S}_{\text{in}}$ 是入射粒子的流密度, $\hat{S}_{\text{scatt}}$ 是出射流密度. 两者都是矢量, 前者方向为 $\hat{z}$, 后者方向为 $\hat{r}$.
单位时间内穿过横截面 $\mathrm{d}\sigma$ 的入射粒子数为 $\hat{S}_{\text{in}}\mathrm{d}\sigma$; 单位时间内穿过横截面 $r^{2}\mathrm{d}\Omega$ 的出射粒子数为 $\hat{S}_{\text{scatt}}r^{2}\mathrm{d}\Omega$.
根据粒子数守恒可以导出
$$ \hat{S}_{\text{scatt}}r^{2}\mathrm{d}\Omega = \hat{S}_{\text{in}}\mathrm{d}\sigma $$
所以微分散射截面可以写作
$$ \frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}\mathrm{d}\Omega = \frac{\hat{S}_{\text{scatt}}r^{2}\mathrm{d}\Omega}{\hat{S}_{\text{in}}} = \frac{\text{单位时间散射到}\mathrm{d}\Omega\text{内的粒子数}}{\text{单位时间入射到单位横截面内的粒子数}} $$
所以总散射截面为
$$ \sigma = \int\mathrm{d}\sigma = \int\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}\mathrm{d}\Omega $$
如果散射势能 $V(\vec{r})$ 处处非 $0$, 那么所有入射粒子均被散射, 也就是说总散射截面将会无穷大.
经典硬球模型
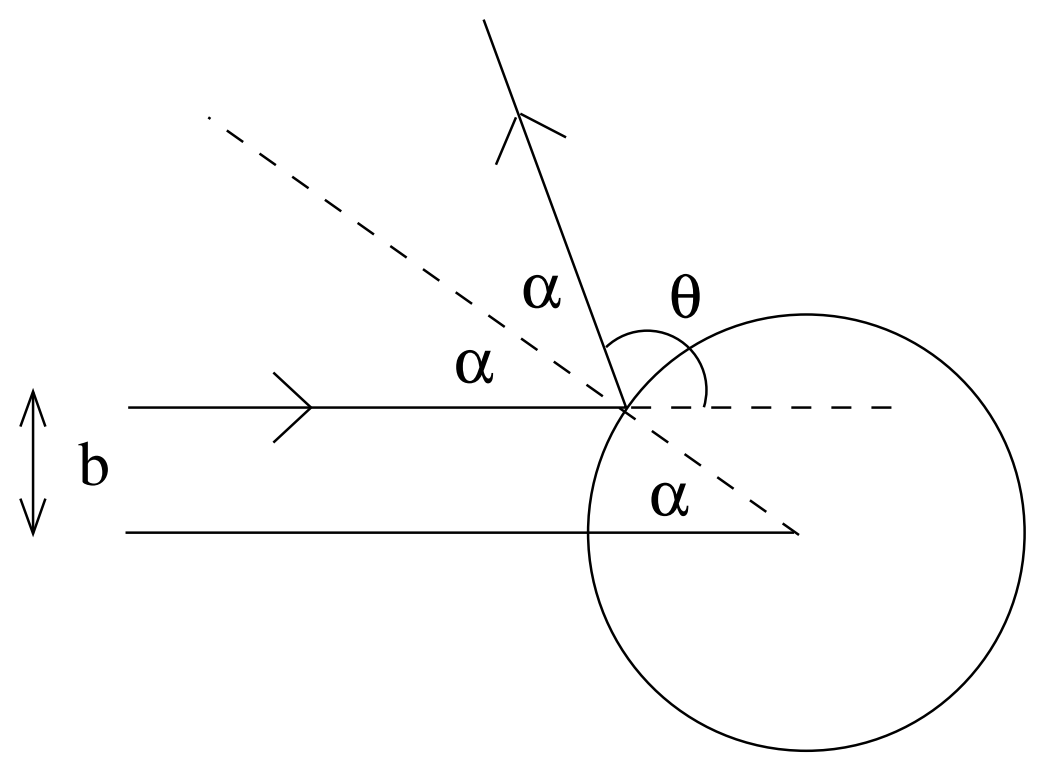
硬球半径为 $R$, 只有 $b < R$ 的粒子束部分才会被散射.
$$ b = R\sin{\alpha} = R\sin{\left(\frac{\pi}{2}-\frac{\theta}{2}\right)} = R\cos{\frac{\theta}{2}} $$
所以微分散射截面为
$$ \frac{\mathrm{d}\sigma}{\mathrm{d}\Omega} = \frac{R^{2}\cos{\left(\frac{\theta}{2}\right)}\sin{\left(\frac{\theta}{2}\right)}}{2\sin{\theta}} = \frac{R^{2}}{4} $$
对其积分即有总散射截面:
$$ \sigma = \iint\sin{\theta}\mathrm{d}\theta\mathrm{d}\phi\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega} = \pi R^{2} $$
这正是硬球的最大横截面面积. 这是一个纯粹的几何问题.
经典卢瑟福散射
散射势能
$$ V(r) = \frac{q_{1}q_{2}}{4\pi\epsilon_{0}r} $$
经典力学推导出
$$ 2bE = \frac{q_{1}q_{2}}{4\pi\epsilon_{0}}\cot{\left(\frac{\theta}{2}\right)} $$
微分散射截面
$$ \frac{\mathrm{d}\sigma}{\mathrm{d}\Omega} = \left(\frac{q_{1}q_{2}}{16\pi\epsilon_{0}E\sin^{2}{\left(\frac{\theta}{2}\right)}}\right)^{2} $$
取小角度近似 $(\theta\ll 1)$, 将会有 $\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}\approx\theta^{-4}$, 所以总散射截面:
$$ \sigma = \int\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}\mathrm{d}\Omega\approx\int\theta^{-4}\sin{\theta}\mathrm{d}\theta\mathrm{d}\phi \rightarrow\infty $$
量子散射理论
背景
量子力学中考虑的散射, 其物理图像应当如何考虑? 一个波包从无穷远处入射, 并且与散射源相互作用, 最后出射到无穷远.
求解波函数的边界条件为粒子从无穷远处以平面波入射, 并且以球面波入射到无穷远. 这正是入射粒子流的稳态情况.
下面的讨论均为 不含时 的散射.
定态薛定谔方程的求解
$$ \left(-\frac{\hbar^{2}}{2m}\nabla^{2} + V(\mathbf{r})\right)\psi(\mathbf{r}) = E\psi(\mathbf{r}) $$
假定无穷远处势能为 $0$, 粒子动量为 $\hbar\mathbf{k}$, 因此
$$ E = \frac{\hbar^{2}\mathbf{k}^{2}}{2m},\quad k = \frac{2mE}{\hbar} $$
为了便于研究, 势能只有在 $r< a$ 区域非零, 即 散射区域, 而 中间区域 势能为 $0$. 最外面的 辐射区域 中, 粒子的角动量可以忽略.
因此有
$$ -\frac{\hbar^{2}}{2m}\nabla^{2}\psi(\mathbf{r}) = E\psi(\mathbf{r}) $$
波函数可以展开为球谐函数的级数:
$$ \psi(\mathbf{r}) = \sum_{l,m}\frac{u_{l}(r)}{r}c_{lm}Y_{lm}(\theta,\phi) $$
我们可以去粒子入射方向为 $\hat{z}$, 所以在势能具有求对称性的情况下, 总波函数将会有 $\hat{z}$ 轴的对称性, 即对于 $m\neq 0$ 的项均为 $0$.
使用分离变量法可以得到
散射区域的径向方程:
$$ \left(-\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}} + \frac{l(l + 1)}{r^{2}} + \frac{2mV(r)}{\hbar^{2}}\right)u_{l}(r) = k^{2}u_{l}(r) $$
中间区域的径向波函数:
$$ \left(-\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}} + \frac{l(l + 1)}{2}\right)u_{l}(r) = k^{2}u_{l}(r) $$
为了对表达式进行简化, 我们可以引入标记 $\rho = kr$, 将上面方程改写为
$$ \begin{aligned} \left(-\frac{\mathrm{d}^{2}}{\mathrm{d}\rho^{2}} + \frac{l(l + 1)}{\rho^{2}}\right)u_{l}(\rho) &= u_{l}(\rho)\\ \left(-\frac{1}{\rho}\frac{\mathrm{d}^{2}}{\mathrm{d}\rho^{2}}\rho + \frac{l(l + 1)}{\rho^{2}}\right)R_{l}(r) &= R_{l}(r) \end{aligned} $$
根据常微分实方程相关结论, 可以使用通解:
$$ u_{l}(\rho) = A_{l}\rho j_{l}(\rho) + B_{l}\rho n_{l}(\rho) $$
换为原本的 $r$ 变量:
$$ u_{l}(\color{red}{r}) = A_{l} \color{red}{r}j_{l}(k\color{red}{r}) + B_{l} \color{red}{r} n_{l}(k\color{red}{r}) $$
$j_{l}(x), n_{l}(x)$ 分别为第一类球贝塞尔函数和第二类球贝塞尔函数. 其近场和远场的渐进行为是 $$ \rho\ll 1(\text{近场}):\begin{cases} j_{l}(\rho)\approx\frac{\rho^{l}}{(2l + 1)!!}\\ n_{l}(\rho)\approx -\frac{(2l - 1)!!}{\rho^{l + 1}} \end{cases}\\ \rho\gg 1(\text{远场}):\begin{cases} j_{l}(\rho)\approx\frac{\sin{\left(\rho-\frac{l\pi}{2}\right)}}{\rho}\\ n_{l}(\rho)\approx-\frac{\cos{\left(\rho - \frac{l\pi}{2}\right)}}{\rho} \end{cases} $$
原点处, $j_{l}(\rho)\rightarrow 0, n_{l}(\rho)\rightarrow\infty$
在辐射区域, 即远场近似, 忽略角动量项:
$$ -\frac{\mathrm{d}^{2}}{\mathrm{d}\rho^{2}}u_{l}(\rho) = u_{l}(\rho) $$
Hankel 函数
球贝塞尔函数可以写作球 Hankel 函数的线性组合: $$ h_{l}^{(1)}(\rho) = j_{l}(\rho) + i n_{l}(\rho)\\ h_{l}^{(2)}(\rho) = j_{l}(\rho) - i n_{l}(\rho) $$
球 Hankel 函数在远场的渐进行为:
$$ \begin{aligned} \text{出射球面波:}h_{l}^{(1)}(\rho) \approx (-i)^{l+1}\frac{e^{i\rho}}{\rho} &= \frac{1}{i}\frac{e^{i\left(\rho-\frac{l\pi}{2}\right)}}{\rho}\\ \text{入射球面波:}h_{l}^{(2)}(\rho) \approx i^{l + 1}\frac{e^{-i\rho}}{\rho} &=-\frac{1}{i}\frac{e^{-i\left(\rho - \frac{l\pi}{2}\right)}}{\rho} \end{aligned} $$
径向波函数重新写为
$$ u_{l}(\rho) = A_{l}’\rho h_{l}^{(1)} + B_{l}’\rho h_{l}^{(2)}(\rho) $$
的形式.
在辐射区域使用远场近似:
$$ \psi(\mathbf{r})\approx e^{ikz} + \sum_{l,m}\left(A_{l}’\frac{e^{i\rho}}{\rho} + B_{l}’\frac{e^{-i\rho}}{\rho}\right)c_{lm}Y_{lm}(\theta,\phi) $$
第一项是 入射平面波, 第二项是 散射球面波.
我们也可以将入射波按照同样的方式进行 Hankel 波函数展开, 但是没有这个必要.
因为第二项的运动应该是由散射中心向无穷远处运动, 这个与向中心汇聚的入射球面波的物理过程不符合.
在辐射区域, 波函数的远场近似为
$$ \lim_{r\rightarrow\infty}\psi(\mathbf{r}) = \psi_{\text{in}} + \psi_{\text{scatt}} = e^{ikz} + f(\theta,\phi)\frac{e^{ikr}}{r} $$
$$ \begin{aligned} \text{入射平面波:}\psi_{\text{in}} &= e^{ikz}\\ \text{散射球状波:}\psi_{\text{scatt}} &= f(\theta,\phi)\frac{e^{ikr}}{r} \end{aligned} $$
$f(\theta,\phi)$ 是散射振幅: $$ f(\theta,\phi) = \sum_{l,m}k^{-1}A_{l}‘c_{lm}Y_{lm}(\theta,\phi) $$
薛定谔方程具有时间对称性, 所以原解的复共轭
$$ \lim_{r\rightarrow\infty}\psi^{*} = e^{-ikz} + f^{*}(\theta,\phi)\frac{e^{-ikr}}{r} $$
但是这个解无法在实验上真正观察到, 因为我们只能测量局部的物理量或者散射实验中的某些特定角度, 而无法玩确定波函数的形式.
概率流与散射截面
概率流
$$ \mathbf{S} = \frac{\hbar}{m}\text{Im}\left(\psi^{*}\nabla\psi\right) $$
在定态中, 概率流满足
$$ \nabla\cdot\mathbf{S} = 0 $$
将远场近似的波函数代入到概率流的表达式:
$$ \begin{aligned} \mathbf{S} &= \frac{\hbar}{m}\text{Im}\left[\left(\psi^{*}_{\text{in}} + \psi^{*}_{\text{scatt}}\right)\nabla\left(\psi_{\text{in}} + \psi_{\text{scatt}}\right)\right]\\ & = \frac{\hbar}{m}\text{Im}\left(\psi^{*}_{\text{in}}\nabla\psi_{\text{in}}\right) + \frac{\hbar}{m}\text{Im}\left(\psi^{*}_{\text{scatt}}\nabla\psi_{\text{scatt}}\right) + \left(\text{交叉项}\right) \end{aligned} $$
第一项是入射波的概率流, 第二项是散射波的概率流.
由于实验中入射光的宽度有限, 所以交叉项在实验中无法被观测到. 所以我们可以这样处理: **总概率流是入射与散射的线性叠加.
入射概率流为
$$ \mathbf{S}_{\text{in}} = \frac{\hbar}{m}\text{Im}\left(e^{-ikz}\nabla e^{ikz}\right) = \frac{\hbar k}{m}\hat{z} = v\hat{z} $$
$v = \frac{\hbar k}{m}$, 为入射波的速度. 入射概率流的大小就是速度, 方向为 $\hat{z}$.
Nabla 算子的球坐标下的表示为
$$ \nabla = \hat{r}\frac{\partial }{\partial r} + \frac{\hat{\theta}}{r}\frac{\partial }{\partial\theta} + \frac{\hat{\varphi}}{r\sin{\theta}}\frac{\partial }{\partial\varphi} $$
所以散射概率流为
$$ \mathbf{S}_{\text{scatt}} = \frac{\hbar}{m}\text{Im}\left[\frac{1}{r}e^{-ikr}f^{*}(\theta,\varphi)\nabla\frac{1}{r}e^{ikr}f(\theta,\varphi)\right] $$
辐射区域内, 因为远场近似即有 $\frac{1}{r}$ 是小量.
只取 $\frac{1}{r}$ 的最低阶:
$$ \nabla\frac{1}{r}e^{ikr}f(\theta,\varphi) = \frac{ik\hat{r}}{r}e^{ikr}f(\theta,\varphi) + \mathcal{O}\left(\frac{1}{r^{2}}\right) $$
所以将上述结果重新代入到散射概率流中:
$$ \begin{aligned} \mathbf{S}_{\text{scatt}} &\approx \frac{\hbar}{m}\text{Im}\left\{\frac{1}{r}e^{-ikr}f^{*}\frac{ik\hat{r}}{r}e^{ikr}f\right\}\\ & = \frac{\hbar k}{m}\frac{\hat{r}}{r^{2}}|f|^{2} + \mathcal{O}\left(\frac{1}{r^{3}}\right)\\ & = \frac{\hbar k|f|^{2}}{mr^{2}}\hat{r} + \mathcal{O}\left(\frac{1}{r^{3}}\right) \end{aligned} $$
单位时间内穿过立体角 $\mathrm{d}\Omega$ 的被散射粒子数:
$$ \mathbf{S}_{\text{scatt}}\cdot\mathrm{d}\mathbf{\sigma} = \frac{\hbar k|f|^{2}}{mr^{2}}r^{2}\mathrm{d}\Omega = \frac{\hbar k|f|^{2}}{m}\mathrm{d}\Omega $$
单位时间穿过单位横截面的入射粒子数为
$$ \mathbf{S}_{\text{in}}\cdot\hat{z} = \frac{\hbar k}{m} $$
将上述讨论代入到经典的散射理论中:
$$ \frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}(\theta,\varphi) = \frac{|\mathbf{S}_{\text{scatt}}\cdot\mathrm{d}\mathbf{a}|}{|\mathbf{S}_{\text{in}}\cdot\hat{z}|} = |f(\theta,\varphi)|^{2} $$
总散射截面即为上式对立体角求积分:
$$ \sigma = \int\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}(\theta,\varphi)\mathrm{d}\Omega $$
概率流交叉项
$$ \begin{aligned} \left(\text{交叉项}\right) &= \frac{\hbar}{m}\text{Im}\left[e^{-ikz}\nabla\frac{f}{r}e^{ikr} + e^{ikz}\nabla\frac{f^{*}}{r}e^{-ikr}\right]\\ & = \frac{\hbar}{m}\text{Im}\left[e^{-ikz}\frac{f}{r}e^{ikr}ik\hat{r} + e^{ikz}\frac{f^{*}}{r}e^{-ikr}(-ik)\hat{r}\right] \end{aligned} $$
分波法
推导
瑞利公式 $$ \begin{aligned} e^{ikz} & = \sqrt{4\pi}\sum_{l=0}^{\infty}\sqrt{2l+1}i^{l}Y_{l0}(\theta)j_{l}(kr)\\ & = \sum_{l = 0}^{\infty}(2l + 1)i^{l}P_{l}(\cos{\theta})j_{l}(kr)\\ & = \sqrt{4\pi}\sum_{l = 0}^{\infty}\sqrt{2l + 1}i^{l}Y_{l0}\frac{1}{2}\left(h_{l}^{(1)}(kr) + h_{l}^{(2)}(kr)\right)\\ & \approx\sqrt{4\pi}\sum_{l = 0}^{\infty}\sqrt{2l + 1}i^{l}Y_{l0}(\theta)\frac{1}{2i}\left(\frac{e^{i\left(kr-\frac{l\pi}{2}\right)}}{kr} - \frac{e^{-i\left(kr - \frac{l\pi}{2}\right)}}{kr}\right) \end{aligned} $$
第一项和第二项分别为发散和汇聚的球面波.
对于散射波函数, 在散射区域外可以写出
$$ \psi(\mathbf{r}) = \sqrt{4\pi}\sum_{l = 0}^{\infty}\sqrt{2l + 1}i^{l}Y_{l0}(\theta)\frac{1}{2}\left(\hat{A}_{l}h_{l}^{(1)}(kr) + \hat{B}_{l}h_{l}^{(2)}(kr)\right) $$
使用远场近似:
$$ \psi(\mathbf{r}) = \sqrt{4\pi}\sum_{l = 0}^{\infty}\sqrt{2l + 1}i^{l}Y_{l0}(\theta)\frac{1}{2i}\left(\hat{A}_{l}\frac{e^{i\left(kr - \frac{l\pi}{2}\right)}}{kr} - \hat{B}_{l}\frac{e^{-i\left(kr-\frac{l\pi}{2}\right)}}{kr}\right) $$
$$ \psi_{\text{scatt}} = \psi(\mathbf{r}) - e^{ikz}\approx f(\theta,\phi)\frac{e^{ikr}}{r} $$ 这个球面波发散.
所以 $\hat{B}_{l} = 1$.
入射波函数为
$$ \begin{aligned} (\psi_{l})_{\text{in}} & = \left(h_{l}^{(1)}(kr) + h_{l}^{(2)}(kr)\right)Y_{l0}(\theta,\phi)\\ & \approx\frac{1}{i}\left(\frac{e^{i\left(kr - \frac{l\pi}{2}\right)}}{kr} - \frac{e^{-i\left(kr - \frac{l\pi}{2}\right)}}{kr}\right)Y_{l0}(\theta,\phi) \end{aligned} $$
在散射区域外面, 入射波和散射波的总和为
$$ \psi_{l} = \left(\hat{A}_{l}h_{l}^{(1)}(kr) + h_{l}^{(2)}(kr)\right)Y_{l0}(\theta,\phi)\rightarrow \frac{1}{i}\left(\hat{A}_{l}\frac{e^{i\left(kr-\frac{l\pi}{2}\right)}}{kr} - \frac{e^{-i\left(kr-\frac{l\pi}{2}\right)}}{kr}\right)Y_{l0}(\theta,\phi) $$
现在根据波函数来计算概率流:
$$ \mathbf{S}_{\text{tot}} = \frac{\hbar}{m}\text{Im}(\psi_{l}^{*}\nabla\psi_{l}) = \frac{\hbar\hat{r}}{mkr^{2}}\left(|\hat{A}_{l}|^{2} - 1\right)|Y_{l0}(\theta,\phi)|^{2} + \mathcal{O}\left(\frac{1}{r^{3}}\right) $$
$|Y_{l0}(\theta,\phi)|^{2}$ 恒正.
为了满足概率流守恒, 也就是定态下, 使半径足够大, 球面的通量为 $0$:
$$ \oint\mathbf{S}_{\text{tot}}\cdot\mathrm{d}\mathbf{a} = \iint r^{2}\mathrm{d}\Omega\frac{\hbar}{mkr^{2}}\left(|\hat{A}_{l}|^{2} - 1\right)Y_{l0}(\theta,\phi)^{2} = \frac{\hbar}{mk}\left(|\hat{A}_{l}|^{2} - 1\right) = 0\\ \Downarrow\\ |\hat{A}_{l}| = 1 \Rightarrow \hat{A}_{l} = e^{2i\delta_{l}} $$
$\delta_{l}$ 即为 相移.
将 $\hat{A}_{l} = e^{2i\delta_{l}}$ 和 $\hat{B} = 1$ 代入到 $\psi_{l}$ 中, 得到
$$ \begin{aligned} \psi_{l} & = \left(e^{2i\delta_{l}}h_{l}^{(1)}(kr) + h_{l}^{(2)}(kr)\right)Y_{l0}(\theta,\phi)\\ & \rightarrow \frac{1}{i}\left(\frac{e^{i\left(kr-\frac{l\pi}{2} + 2\delta_{l}\right)}}{kr} - \frac{e^{-i\left(kr-\frac{l\pi}{2}\right)}}{kr}\right)Y_{l0}(\theta,\phi) \end{aligned} $$
对于平面波的入射波函数, 在散射区域外的总波函数为
$$ \psi(\mathbf{r}) = \sqrt{4\pi}\sum_{l = 0}^{\infty}\sqrt{2l + 1}i^{l}Y_{l0}(\theta)\frac{1}{2}\left(e^{2i\delta_{l}}h_{l}^{(1)}(kr) + h_{l}^{(2)}(kr)\right) $$
采用远场近似, 即有
$$ \psi(\mathbf{r}) = \sqrt{4\pi}\sum_{l = 0}^{\infty}\sqrt{2l + 1}i^{l}Y_{l0}(\theta)\frac{1}{2i}\left(\frac{e^{i\left(kr-\frac{l\pi}{2} + 2\delta_{l}\right)}}{kr} - \frac{e^{-i\left(kr - \frac{l\pi}{2}\right)}}{kr}\right) $$
和 $$ e^{ikz} \approx \sqrt{4\pi}\sum_{0}^{\infty}\sqrt{2l + 1}i^{l}Y_{l0}(\theta)\frac{1}{2i}\left(\frac{e^{i\left(kr-\frac{l\pi}{2}\right)}}{kr} - \frac{e^{-i\left(kr-\frac{l\pi}{2}\right)}}{kr}\right) $$ 相比, 发散球面波的系数发生了相移 $e^{2i\delta_{l}}$.
即有
$$ \begin{aligned} \frac{f(\theta,\phi)}{r}e^{ikr} & = f(\mathbf{r}) - e^{ikz}\\ & = \sqrt{4\pi}\sum_{l=0}^{\infty}\sqrt{2l + 1}i^{l}Y_{l0}(\theta)\frac{1}{2i}\left[\frac{e^{i\left(kr-\frac{l\pi}{2} + 2\delta_{l}\right)}}{kr} - \frac{e^{i\left(kr-\frac{l\pi}{2}\right)}}{kr}\right]\\ & = \sqrt{4\pi}\sum_{l=0}^{\infty}\sqrt{2l + 1}Y_{l0}(\theta)\frac{1}{2i}\left[\frac{e^{i\left(kr + 2\delta_{l}\right)}}{kr} - \frac{e^{ikr}}{kr}\right]\\ & = \frac{\sqrt{4\pi}}{k}\sum_{l=0}^{\infty}\sqrt{2l + 1}Y_{l0}(\theta)e^{i\delta_{l}}\sin{(\delta_{l})}\frac{e^{ikr}}{r} \end{aligned} $$
散射振幅的球谐函数展开为
$$ f(\theta) = \frac{\sqrt{4\pi}}{k}\sum_{l=0}^{\infty}\sqrt{2l + 1}e^{i\delta_{l}}\sin{(\delta_{l})}Y_{l0}(\theta)\\ = \frac{1}{k}\sum_{l = 0}^{\infty}(2l + 1)e^{i\delta_{l}}\sin{(\delta_{l})}P_{l}(\theta)\\ = \frac{1}{k}\sum_{l = 0}^{\infty}(2l + 1)P_{l}(\theta)\frac{e^{2i\delta_{l}} - 1}{2i} $$
所以总散射截面:
$$ \sigma = \int\mathrm{d}\sigma = \int\mathrm{d}\Omega\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega} = 2\pi\int_{0}^{\pi}|f(\theta)|^{2}\mathrm{d}(\sin{\theta})\mathrm{d}\theta $$
勒让德多项式的正交性
$$ \int_{-1}^{1}\mathrm{d}x P_{l}(x)P_{l’}(x) = \frac{2\delta_{ll’}}{2l + 1} $$
所以总散射截面的表达式化为
$$ \sigma = \frac{4\pi}{k^{2}}\sum_{l=0}^{\infty}(2l + 1)\sin^{2}\delta_{l} $$
前进方向的散射振幅为
$$ f_{\theta = 0} = \frac{1}{k}\sum_{l = 0}^{\infty}(2l + 1)e^{i\delta_{l}}\sin{(\delta_{l})} $$
其虚部为
$$ \text{Im}f_{\theta=0} = \frac{1}{k}\sum_{l}^{\infty}(2l + 1)\sin^{2}{(\delta_{l})} $$
对比总散射截面的表达式, 将上式代入:
$$ \sigma = \frac{4\pi}{k}\text{Im}f_{\theta=0} $$
这就是 光学定理.
对于总散射截面, 求和可以理解为多个分波:
$$ \sigma = \frac{4\pi}{k^{2}}\sum_{l=0}^{\infty}(2l + 1)\sin^{2}\delta_{l} = \sum_{l = 0}^{\infty}\sigma_{l} $$
标记为 $l$ 的分波, 其上限为 $$ \sigma_{l}^{\text{max}} = \frac{4\pi(2l + 1)}{k^{2}} $$ 这个上限被称作幺正限制.
第一类球贝塞尔函数的近场近似: $$ (ka\ll 1)\quad j_{l}(\rho)\approx\frac{\rho^{l}}{(2l + 1)!!},\quad\rho\ll 1 $$ 取对数, 并且使用斯特林公式: $$ \log{j_{l}(\rho)} \approx l\log{\frac{\rho}{l}} $$ 对于大角动量, 即 $\rho < l$ 区域下, $\log{j_{l}(\rho)}$ 将是指数减小, 所以 $\rho = ka < l$ 下, 势能对入射波函数的影响也是指数减小, 从而基本没有散射.
在散射区域外面, 径向波函数为
$$ R_{l}(r) = e^{i\delta_{l}}h_{l}^{(1)}(kr) + h_{l}^{(2)}(kr) = 2e^{i\delta_{l}}[\cos{(\delta_{l})}j_{l}(kr) - \sin{(\delta_{l})}n_{l}(kr)] $$
其相位是一个常数, 并不随着 $r$ 变化, 并且
$$ \tan{\delta_{l}} = -\frac{c_{n_{l}}}{c_{j_{l}}} $$
也就是说, 如果散射区域外的总径向波函数的形式为
$$ R_{l}(r) = A_{l}j_{l}(kr) + B_{l}n_{l}(kr) $$
那么
$$ \tan{\delta_{l}} = -\frac{B_{l}}{A_{l}} $$
所以为了确定相移, 只需要确定两个系数的比值即可.
硬球散射
势能函数
$$ V(\mathbf{r}) = \begin{cases} \infty,&\quad r\leq a\\ 0,&\quad r > a \end{cases} $$
中间区域和辐射区域的径向波函数为
$$ R_{l}(r) = A_{l}j_{l}(kr) + B_{l}n_{l}(kr) $$
边界条件为波函数在球面上处处为 $0$:
$$ R_{l}(a) = A_{l}j_{l}(ka) + B_{l}n_{l}(ka) = 0 $$
所以相移可以由
$$ \tan{\delta_{l}} = -\frac{B_{l}}{A_{l}} = \frac{j_{l}(ka)}{n_{l}(ka)}\\ \sin^{2}\delta_{l} = \frac{\tan^{2}\delta_{l}}{1 + \tan^{2}\delta_{l}} = \frac{j_{l}^{2}(ka)}{j_{l}^{2}(ka) + n_{l}^{2}(ka)} $$
所以硬球散射的总散射截面化为
$$ \sigma = \frac{4\pi}{k^{2}}\sum_{l}(2l + 1)\frac{j_{l}^{2}(ka)}{j_{l}^{2}(ka) + n_{l}^{2}(ka)} $$
球贝塞尔函数在低能极限 $ka\ll 1$ 的渐进行为: $$ \text{近场}\rho\ll 1: \begin{cases} j_{l}(\rho) \approx \frac{\rho^{l}}{(2l + 1)!!}\\ n_{l}(\rho) \approx -\frac{(2l - 1)!!}{\rho^{l + 1}}\gg j_{l}(\rho) \end{cases} $$
$$ \lim_{\delta_{l}\ll 1}\delta_{l}\approx\frac{j_{l}(ka)}{n_{l}(ka)}\approx-\frac{(ka)^{2l + 1}}{(2l + 1)!!(2l -1)!!}, \quad ka\ll 1 $$
因为 $ka$ 可以足够小, 所以将总截面展开 $ka$ 级数时只需要保留第一项:
$$ \sigma\approx\frac{4\pi}{k^{2}}(ka)^{2} = 4\pi a^{2} $$
这就是总散射截面的低能极限, 是经典硬球散射总截面的四倍.
相移一般公式
散射区域 $r < a$ 内的波函数为 $R_{l}(r)$, 散射区域外的径向波函数则是由
$$ R_{l}(r) = A_{l}j_{l}(kr) + B_{l}n_{l}(kr) $$
给出, 波函数的连续性方程有
$$ R_{l}(a) = A_{l}j_{l}(ka) + B_{l}n_{l}(ka)\\ aR_{l}’(a) = ka(A_{l}j_{l}’(ka) + B_{l}n_{l}’(ka)) $$
引入标记
$$ \beta_{l} = \frac{aR_{l}’(a)}{R_{l}(a)} $$
即有
$$ \beta_{l} = ka\frac{A_{l}j_{l}’(ka) + B_{l}n_{l}’(ka)}{A_{l}j_{l}(ka) + B_{l}n_{l}(ka)} = ka\frac{j_{l}’(ka) - \tan{\delta_{l}}n_{l}’(ka)}{j_{l}(ka) - \tan{\delta_{l}}n_{l}(ka)} $$
所以相移的值为
$$ \tan{\delta_{l}} = \frac{j_{l}(ka) - \frac{ka}{\beta_{l}}j_{l}’(ka)}{n_{l}(ka) - \frac{ka}{\beta}n_{l}’(ka)} $$
如果要用 $\beta_{l}$ 来表示因子 $e^{2i\delta_{l}}$, 即有
$$ \begin{aligned} e^{2i\delta_{l}} &= -\frac{ka(j_{l}’ - in_{l}’) - \beta(j_{l} - in_{l})}{ka(j_{l}’ + in_{l}’) - \beta(j_{l} + in_{l})}\\ &= -\left(\frac{j_{l} - in_{l}}{j_{l} + in_{l}}\right)\left[\frac{\beta_{l} - ka\left(\frac{j_{l}’-in_{l}’}{j_{l}’ + in_{l}’}\right)}{\beta_{l}- ka\left(\frac{j_{l}’-in_{l}’}{j_{l}’ + in_{l}’}\right)}\right] \end{aligned} $$
后面的系数即为相移影响.
玻恩近似
Intro
现在我们讨论更一般的情形, 即 $V(\mathbf{r})$ 去除球对称性.
波函数的远场近似为
$$ \psi(\mathbf{r}) = e^{ikz} + \psi_{\text{scatt}} = e^{ikz} + \frac{f(\theta,\phi)}{r}e^{ikr} $$
$f(\theta,\phi)$ 为散射振幅.
散射截面为
$$ \frac{\mathrm{d}\sigma(\theta,\phi)}{\mathrm{d}\Omega} = |f(\theta,\phi)|^{2} $$
原本的薛定谔方程为
$$ -\frac{\hbar^{2}}{2m}\nabla^{2}\psi + V(\mathbf{r})\psi = E\psi,\quad E> 0 $$
现在改写为
$$ (\nabla^{2} + k^{2})\psi = U(\mathbf{r})\psi $$
$$ k = \frac{\sqrt{2mE}}{\hbar}, U(\mathbf{r}) = \frac{2mV(\mathbf{r})}{\hbar} $$
我们并不能将上述方程写作 $$ \psi = (\nabla^{2} + k^{2})^{-1}U\psi $$ 因为算符 $(\nabla^{2} + k^{2})$ 具有 $0$ 本征值, 所以并不可逆.
格林函数
亥姆霍兹方程:
$$ (\nabla^{2} + k^{2})G(\mathbf{r}) = -\delta(\mathbf{r}) $$
如果 $G(\mathbf{r})$ 是该方程的解, 那么 $G(\mathbf{r}) + e^{i\mathbf{k}\cdot\mathbf{r}}$ 也是方程解. 这是因为 $e^{i\mathbf{k}\cdot\mathbf{r}}$ 是该方程的齐次解.
我们可以引入无穷小量 $\epsilon > 0$:
$$ (\nabla^{2} + k^{2} \pm i\epsilon)G^{\pm}(\mathbf{r}) = -\delta(\mathbf{r}) $$
对 $G^{\pm}(\mathbf{r})$ 进行傅里叶变换, 即有
$$ \begin{aligned} G^{\pm}(\mathbf{r}) &= \int\hat{G}^{\pm}(\mathbf{q})e^{i\mathbf{q}\cdot\mathbf{r}}\frac{\mathrm{d}^{3}q}{(2\pi)^{3}}\\ \hat{G}^{\pm}(\mathbf{q}) &= \int G^{\pm}(\mathbf{r})e^{-i\mathbf{q}\cdot\mathbf{r}}\mathrm{d}^{3}r \end{aligned} $$
于是有变换后的添加小量参数 $\epsilon$ 的薛定谔方程:
$$ (-a^{2} + k^{2} \pm i\epsilon)\hat{G}^{\pm}(\mathbf{q}) = -1\\ \Downarrow\\ \hat{G}^{\pm}(\mathbf{q}) = \frac{-1}{-q^{2} + k^{2} \pm i\epsilon} $$
算符 $(\nabla^{2} + k^{2} \pm i\epsilon)$ 的本征函数为平面波, 本征值为 $-q^{2} + k^{2} \pm i\epsilon$. 我们引入的 $\epsilon>0$, 所以 算符 $(\nabla^{2} + k^{2} \pm i\epsilon)$ 可逆.
$G^{\pm}(\mathbf{r})$ 只与 $r = |\mathbf{r}|$, 所以我们可以设 $\mathbf{r} = r\hat{z}$. 令 $\mathbf{q} = (q,\theta,\varphi)$.
球坐标的动量空间体微元为
$$ \int\mathrm{d}^{3}q = \int_{0}^{\infty}q^{2}\mathrm{d}q\int_{0}^{\pi}\sin{\theta}\mathrm{d}\theta\int_{0}^{2\pi}\mathrm{d}\varphi $$
所以对 $e^{i\mathbf{q}\cdot\mathbf{r}}$ 因子进行积分:
$$ \int e^{i\mathbf{q}\cdot\mathbf{r}}\mathrm{d}^{3}q = 2\pi\int_{0}^{\infty}q^{2}\mathrm{d}q\int_{0}^{\pi}e^{iqr\cos{\theta}}\sin{\theta}\mathrm{d}\theta\\ = 2\pi\int_{0}^{\infty}q^{2}\mathrm{d}q\frac{1}{iqr}e^{iqru}|_{-1}^{+1} = 4\pi\int_{0}^{\infty}\frac{\sin{qr}}{qr}q^{2}\mathrm{d}q $$
所以
$$ G^{\pm}(r) = \frac{4\pi}{(2\pi)^{3}}\int_{0}^{\infty}\frac{\sin{qr}}{qr}\frac{-1}{-q^{2} + k^{2} \pm i\epsilon}q^{2}\mathrm{d}q\\ = \frac{-1}{4\pi^{2}r}\int_{-\infty}^{+\infty}\frac{q\sin{(qr)}\mathrm{d}q}{-q^{2}+k^{2}\pm i\epsilon} $$
利用
$$ \frac{-1}{-q^{2} + k^{2} \pm i\epsilon} = \frac{1}{[q-(k\pm i\epsilon)][q+(k\pm i\epsilon)]}\\ \sin{(qr)} = -\frac{i}{2}(e^{iqr} - e^{-iqr})\\ k^{\pm} = k\pm i\epsilon $$
就有
$$ G^{\pm}(r) = \frac{-i}{8\pi^{2}r}\int_{-\infty}^{+\infty}\frac{q(e^{iqr}-e^{-iqr})}{(q-k^{\pm})(q+k^{\pm})}\mathrm{d}q\\ = \frac{-i}{8\pi^{2}r}\left\{\int_{-\infty}^{+\infty}\frac{qe^{iqr}\mathrm{d}q}{(q-k^{\pm})(q+k^{\pm})} - \int_{-\infty}^{+\infty}\frac{qe^{-iqr}\mathrm{d}q}{(q-k^{\pm})(q + k^{\pm})}\right\} $$
留数定理
函数 $F(z)$ 在 $\mathbb{C}$ 内解析, 并且逆时针围绕点 $z_{0}$ 积分, 且 $F(z_{0})\neq 0$, 即有
$$ \oint_{\mathbb{C}}\frac{F(z)}{z-z_{0}} = 2\pi iF(z_{0}) $$
我们借助上述定理进行求解.
- $G^{+}(r)$;
$$ G^{+}(r) = \frac{-i}{8\pi^{2}r}\left\{\int_{-\infty}^{+\infty}\frac{qe^{iqr}\mathrm{d}q}{(q-k^{+})(q+k^{+})} - \int_{-\infty}^{+\infty}\frac{qe^{-iqr}\mathrm{d}q}{(q-k^{+})(q + k^{+})}\right\} $$
先计算第一项积分. 现在取 $\mathbb{C}$ 的上半平面作围道, 即有
$$ \begin{aligned} I_{1} &= \oint_{\mathbb{C},\text{Im}(q)>0}\frac{qe^{iqr}\frac{1}{q + k^{+}}}{(q-k^{+})}\mathrm{d}q\\ &= (2\pi i)\frac{k^{+}e^{ik^{+}r}}{2k^{+}} = \pi i e^{ik^{+}r}\stackrel{\epsilon\rightarrow 0}{\longrightarrow} \pi i e^{ikr} \end{aligned} $$
同理
$$ \begin{aligned} I_{2} &= \oint_{\mathbb{C},\text{Im}(q)<0}\frac{qe^{-iqr}\frac{1}{q - k^{+}}}{(q+k^{+})}\mathrm{d}q\\ &= -(2\pi i)\frac{-k^{+}e^{ik^{+}r}}{-2k^{+}} = -\pi i e^{ik^{+}r}\stackrel{\epsilon\rightarrow 0}{\longrightarrow} -\pi i e^{ikr} \end{aligned} $$
所以就有
$$ G^{+}(r) = \frac{-i}{8\pi^{2}r}(I_{1} - I_{2}) = \frac{1}{4\pi r}e^{ikr} $$
这就是向外传播的球面波.
$$ \lim_{k\rightarrow 0}G^{+}(r) = \frac{1}{4\pi r},\quad(\text{即库伦势能}) $$
同理, 我们计算 $G^{-}(r)$.
$$ G^{-}(r) = \frac{-i}{8\pi^{2}r}\left\{\int_{-\infty}^{+\infty}\frac{qe^{iqr}\mathrm{d}q}{(q-k^{-})(q + k^{-})} - \int_{-\infty}^{+\infty}\frac{qe^{-iqr}\mathrm{d}q}{(q - k^{-})(q + k^{+})}\right\} $$
第一个积分:
$$ \begin{aligned} I_{1} &= \oint_{\mathbb{C},q > 0}\frac{qe^{iqr}\frac{1}{q-k^{-}}}{q + k^{-}}\mathrm{d}q\\ & = (2\pi i)\frac{k^{+}e^{-ik^{-}r}}{2k^{-}} = \pi i e^{ik^{-}r}\stackrel{\epsilon\rightarrow 0}{\longrightarrow}\pi ie^{-ikr} \end{aligned} $$
第二项积分:
$$ \begin{aligned} I_{2} &= \oint_{\mathbb{C},q < 0}\frac{qe^{-iqr}\frac{1}{q+k^{-}}}{q - k^{-}}\mathrm{d}q\\ & = -(2\pi i)\frac{k^{+}e^{-ik^{-}r}}{2k^{-}} = -\pi i e^{-ik^{-}r}\stackrel{\epsilon\rightarrow 0}{\longrightarrow}-\pi ie^{-ikr} \end{aligned} $$
所以就有
$$ G^{-}(r) = \frac{-i}{8\pi^{2}r}(I_{1} - I_{2}) = \frac{e^{-ikr}}{4\pi r} $$
这是向中心汇聚的球面波.
综上所述, 我们得到了亥姆霍兹的两个解:
$$ G^{\pm}(r) = \frac{e^{\pm ikr}}{4\pi r} $$
$G^{+}(r)$ 是向外传播的球面波, $G^{-}$ 是向心汇聚的球面波. 这个结果在 $\epsilon\rightarrow 0$ 的极限下仍然存在.
我们先讨论最简单的线性组合情况, 即 $G^{+}(r) - G^{-}(r)$. 因为两个单独解都是方程的解, 所以两者的差也是方程的齐次解. 即有
$$ (\nabla^{2} + k^{2})[G^{+}(r) - G^{-}(r)] = 0 $$
$G^{+}(r) - G^{-}(r)$ 除了原点和无穷远处, 都是解析的.
$$ \lim_{kr\ll 1}(G^{+}(r) - G^{-}(r)) = \lim_{kr\ll 1}\left[\frac{1}{4\pi r}\left(e^{ikr} - e^{-ikr}\right)\right] = -\frac{1}{4\pi r}[2ikr + \mathcal{o}(kr)^{3}] = -\frac{ik}{2\pi} + \mathcal{o}(kr)^{2} $$
所以,
$$ \forall\alpha,\quad G^{\alpha}(r) = \alpha G^{+}(r) + (1-\alpha) G^{-}(r) $$
也是方程的解, 即亥姆霍兹方程有无穷多的格林函数. 具体的选取需要根据具体的边界条件确定. 对于散射问题, 需要选择 $G^{\alpha} = G^{+}(r)$, 因为只有向外传播的球面波才是被允许的.
波恩级数
非齐次亥姆霍兹方程
$$ (\nabla^{2} + k^{2})\psi(\mathbf{r}) = -f(\mathbf{r}) $$
的解可以表示为积分
$$ \psi(\mathbf{r}) = \psi_{0}(\mathbf{r}) - \int G^{\pm}(|\mathbf{r} - \mathbf{r}’|)f(\mathbf{r}’)\mathrm{d}^{3}\mathbf{r}’ $$
$\psi_{0}(r)$ 是任意齐次解.
$$ (\nabla^{2} + k^{2})\psi = \color{red}{U(\mathbf{r})\psi}, \quad k = \frac{\sqrt{2mE}}{\hbar},\quad U(\mathbf{r}) = \frac{2mV(\mathbf{r})}{\hbar^{2}} $$
现在将 $\color{red}{U(\mathbf{r})\psi}$ 作为已知函数从而使用非齐次亥姆霍兹方程的结论, 即有方程的形式解
$$ \psi(\mathbf{r}) = e^{ikz} - \frac{m}{2\pi\hbar^{2}}\int\frac{e^{ik|\mathbf{r} - \mathbf{r}’|}}{|\mathbf{r} - \mathbf{r}’|}V(\mathbf{r}’)\psi(\mathbf{r}’)\mathrm{d}^{3}\mathbf{r}' $$
齐次解选为 $e^{ikz}$ (入射平面波), 格林函数选为 $G^{+}(r)$ (向外传播), 上式化为
$$ \psi(\mathbf{r}) = e^{ikz} - \frac{m}{2\pi\hbar^{2}}\int\frac{e^{ik|\mathbf{r}-\mathbf{r}’|}}{|\mathbf{r} - \mathbf{r}’|}V(\mathbf{r}’)\psi(\mathbf{r}’)\mathrm{d}^{3}\mathbf{r}' $$
这并不是真正的解, 而是将薛定谔方程化为另一个等价的方程.
引入积分算符 $\hat{g}$, 用法为
$$ \hat{g}\varphi(\mathbf{r}) = \int\mathrm{d}^{3}\mathbf{r}‘G(\mathbf{r}-\mathbf{r}’)U(\mathbf{r}’)\varphi(\mathbf{r}’) $$
所以形式解可以按照 $\hat{g}$ 算子重写为
$$ |\psi\rangle = |\psi_{0}\rangle - \hat{g}|\psi\rangle $$
所以进一步写出微扰级数
$$ \begin{aligned} |\psi\rangle &= |\psi_{0}\rangle -\hat{g}(|\psi_{0}\rangle - \hat{g}|\psi\rangle)\\ & = |\psi_{0}\rangle - \hat{g}|\psi_{0}\rangle + \hat{g}\hat{g}|\psi_{0}\rangle + \dots\\ & = \left(\hat{I} + \hat{g}\right)^{-1}|\psi_{0}\rangle \end{aligned} $$
$\hat{g}\propto V$, 所以对 $\hat{g}$ 展开就是对 $V$ 展开. 当 $V = 0$, $\psi$ 退化为 $\psi_{0}$, 即没有散射.
一阶玻恩近似
即采用
$$ |\psi\rangle = |\psi_{0}\rangle + \hat{g}|\psi_{0}\rangle $$
那么
$$ \begin{aligned} \psi(\mathbf{r}) &= \psi_{0}(\mathbf{r}) - \int G(\mathbf{r} - \mathbf{r}’)U(\mathbf{r}’)\psi_{0}(\mathbf{r}’)\mathrm{d}^{3}\mathbf{r}’\\ &=e^{ikz} - \int\mathrm{d}^{3}\mathbf{r}’\frac{e^{ik|\mathbf{r}-\mathbf{r}’|}}{4\pi|\mathbf{r}-\mathbf{r}’|}U(\mathbf{r}’)e^{ikz}\\ & = \psi_{\text{in}} + \psi_{\text{scatt}} \end{aligned} $$
所以散射波函数的一级玻恩近似为
$$ \psi_{\text{scatt}} = -\int\mathrm{d}^{3}\mathbf{r}’\frac{e^{ik|\mathbf{r}-\mathbf{r}’|}}{4\pi|\mathbf{r}-\mathbf{r}’|}U(\mathbf{r}’)e^{ikz} $$
$\mathbf{r}$ 是测量散射截面的位置, $\mathbf{r}’$ 是对势能积分的坐标.
$$ \lim_{r\gg r’}|\mathbf{r}-\mathbf{r}’|^{2} = (\mathbf{r}-\mathbf{r}’)\cdot(\mathbf{r}-\mathbf{r}’) = r^{2} + r’^{2} - 2\mathbf{r}\cdot\mathbf{r}’\approx r^{2}\left(1 - \frac{2\mathbf{r}\cdot\mathbf{r}’}{r^{2}}\right) $$
对其开根号即有
$$ |\mathbf{r}-\mathbf{r}’| = \sqrt{r^{2}\left(1 - \frac{2\mathbf{r}\cdot\mathbf{r}’}{r^{2}}\right)}\approx r\left(1 - \frac{\mathbf{r}\cdot\mathbf{r}’}{r^{2}}\right) = r - \hat{r}\cdot\mathbf{r}’ $$
定义出射波矢 $\mathbf{k} = k\hat{r}$, 入射波矢 $\mathbf{k}’ = k\hat{z}$. 即有
$$ \begin{aligned} e^{ik|r-r’|} &\approx e^{ik(r-\hat{r}\cdot\mathbf{r}’)}\approx e^{i(\mathbf{k}\cdot\mathbf{r} - \mathbf{k}\cdot\mathbf{r}’)} + \mathcal{O}\left(\frac{1}{r}\right)\\ e^{ikz} &= e^{i\mathbf{k}’\cdot\mathbf{r}}\\ \frac{1}{|\mathbf{r}-\mathbf{r}’|} &\approx \frac{1}{r} + \mathcal{O}\left(\frac{1}{r^{2}}\right) \approx \frac{1}{r} \end{aligned} $$
使用上述近似:
$$ \psi_{\text{scatt}} = -\int\mathrm{d}^{3}\mathbf{r}’\frac{e^{i(\mathbf{k}\cdot\mathbf{r} - \mathbf{k}\cdot\mathbf{r}’)}}{4\pi r}e^{i\mathbf{k}\cdot\mathbf{r}’}U(\mathbf{r}’) = -\color{red}{\frac{e^{ikr}}{r}}\frac{m}{2\pi\hbar^{2}}\int\mathrm{d}^{3}\mathbf{r}’e^{-i(\mathbf{k}-\mathbf{k’})\cdot\mathbf{r}’}V(\mathbf{r}’) $$
$$ \psi_{\text{scatt}} = \color{red}{\frac{e^{ikr}}{r}}f(\theta,\varphi) $$
观察共有部分既可以得到散射振幅的表达式
$$ f(\theta,\varphi) = -\frac{m}{2\pi\hbar^{2}}\int\mathrm{d}^{3}\mathbf{r}’ e^{-i(\mathbf{k} - \mathbf{k}’)\cdot\mathbf{r}’}V(\mathbf{r}’) $$
引入出射粒子的动量变化:
$$ \mathbf{q} = \mathbf{k} - \mathbf{k}’\\ |\mathbf{q}| = |\mathbf{k} - \mathbf{k}’| = 2k\sin{\frac{\theta}{2}} $$
散射振幅中的积分式本身是一种傅里叶变换, 所以我们可以将其改写为
$$ f(\theta,\varphi) = -\frac{m}{2\pi\hbar^{2}}\hat{V}(\mathbf{q}) $$
$\theta,\varphi$ 是出射动量 $\mathbf{k}$ 的球坐标.
Yukawa 势和库伦势
Yukawa 势
$$ V(r) = -\frac{\beta}{r}e^{-\mu r} $$
先计算出势能的傅里叶变换:
$$ \hat{V}(\mathbf{q}) = \int\mathrm{d}^{e}\mathbf{r} e^{-i\mathbf{q}\cdot\mathbf{r}} V(\mathbf{r}) = \frac{4\pi\beta}{\mu^{2} + q^{2}} $$
将该结果代入到散射振幅中, 即有
$$ f(\theta,\varphi) = -\frac{m}{2\pi\hbar^{2}}\hat{V}(\mathbf{q}) = -\frac{2m\beta}{\hbar^{2}(\mu^{2} + q^{2})} $$
当 $\mu\rightarrow 0,\beta\rightarrow\frac{eQ}{4\pi\epsilon_{0}}$, Yukawa 势能就会退化为库伦势能. ($e$ 为入射粒子的电荷, $Q$ 为散射源的电荷.) 能量为 $E = \frac{\hbar^{2}k^{2}}{2m}$.
那么库伦散射的振幅化为
$$ f(\theta,\varphi) = -\frac{2meQ}{4\pi\epsilon_{0}\hbar^{2}q^{2}} = -\frac{2meQ}{16\pi\epsilon_{0}\hbar^{2}k^{2}\sin^{2}\frac{\theta}{2}} = -\frac{eQ}{16\epsilon_{0}E\sin^{2}{\frac{\theta}{2}}} $$
库伦势能的微分散射截面的一阶玻恩近似为
$$ \frac{\mathrm{d}\sigma}{\mathrm{d}\Omega} = |f|^{2} = \left(\frac{eQ}{16\pi\epsilon_{0}E\sin^{2}\frac{\theta}{2}}\right) $$
和前面的系数差别不一样, 这里计算出来的结果和经典库伦势能给出的结果完全相同.