投影算符
定义
假设对于一个物理量算符 $\hat{R}$, 其本征方程为
$$ \hat{R}|\psi_{k}\rangle = r_{k}|\psi_{k}\rangle\quad(k = 0,1,\dots) $$
我们引入投影算符:
$$ \hat{\pi}_{k} = |\psi_{k}\rangle\langle\psi_{k}| $$
所以显然有
$$ \hat{\pi}_{k}|\psi_{n}\rangle = |\psi_{k}\rangle\langle\psi_{k}|\psi_{n}\rangle = \delta_{kn}|\psi_{k}\rangle $$
性质
- 厄密性
$$ \hat{\pi}_{k} = \hat{\pi}_{k}^{\dagger} $$
- 幂等性(Idempotent)
$$ \hat{\pi}_{k}^{2} = |\psi_{k}\rangle\langle\psi_{k}|\psi_{k}\rangle\langle\psi_{k}|=|\psi_{k}\rangle\langle\psi_{k}|=\hat{\pi}_{k} $$
- 完备性
$$ \sum_{k}\hat{\pi}_{k} = I $$
证明:
对任意的态 $|\psi\rangle$, 都可以将其写作基函数的展开: $$ |\psi\rangle = c_{1}|\psi_{1}\rangle + c_{2}|\psi_{2}\rangle + \dots + c_{n}|\psi_{n}\rangle = \sum_{i}{c_{i}|\psi_{i}\rangle} $$ 那么将投影算符和作用到该态上: $$ \sum_{k}\hat{\pi}_{k}|\psi\rangle = \sum_{k}|\psi_{k}\rangle\langle\psi_{k}|\sum_{i}c_{i}|\psi_{i}\rangle = \sum_{k}\sum_{i}c_{i}|\psi_{k}\rangle\langle\psi_{k}|\psi_{i}\rangle = \\ \sum_{k}\sum_{i}c_{i}\delta_{ki}|\psi_{k}\rangle = \sum_{k}c_{k}|\psi_{k}\rangle = |\psi\rangle $$
所以我们可以得出完备性的结论.
物理量算符
假设对于一个物理量算符 $\hat{R}$, 其本征方程为
$$ \hat{R}|\psi_{k}\rangle = r_{k}|\psi_{k}\rangle\quad(k = 0,1,\dots) $$
对于已知本征方程的物理量算符 $\hat{R}$, 我们可以将其写作:
$$ \hat{R} = \sum_{k}r_{k}\hat{\pi}_{k} $$
这是容易理解的, 因为
$$ \hat{R}|\psi_{n}\rangle = \sum_{k}r_{k}\hat{\pi}_{k}|\psi_{n}\rangle = \sum_{k}r_{k}|\psi_{k}\rangle\langle\psi_{k}|\psi_{n}\rangle = \sum_{k}r_{k}\delta_{kn}|\psi_{k}\rangle = r_{n}|\psi_{n}\rangle $$
即原本的本征方程.
而对于一般性的态 $|\psi\rangle$ 进行物理量 $\hat{R}$ 的测量, 即有
$$ P = \langle\hat{R}\rangle_{\psi} = \langle\psi|\hat{R}|\psi\rangle = \sum_{k}\langle\psi|r_{k}\hat{\pi}_{k}|\psi\rangle = \sum_{k}r_{k}\langle\psi|\hat{\pi}_{k}|\psi\rangle $$
这里我们引入
$$ P_{k} = \langle\psi|\hat{\pi}_{k}|\psi\rangle $$
就有
$$ \langle\hat{R}\rangle_{\psi} = \sum_{k}r_{k}P_{k} $$
$P_{k}$ 的物理含义是指系统状态为 $|\psi\rangle$, 测量物理量 $\hat{R}$ 时的结果为 $r_{k}$ 的概率.
混合态
纯态无法解答的问题
- 测量而未知结果
设自旋 $\frac{1}{2}$ 的系统状态为 $$ |\psi\rangle = \frac{1}{2}\left(|\uparrow\rangle + |\downarrow\rangle\right) $$ 那么我们对系统测量 $\hat{s}_{z}$, 得到结果为 $\pm\frac{1}{2}$ 的概率分别为 $\frac{1}{2}$. 而且我们可以自然而然地作出推论: 如果测量结果为 $\frac{1}{2}$, 那么测量后地系统状态必定为 $|\uparrow\rangle$, 反之亦然.
如果已知对系统做出了 $\hat{s}_{z}$ 的测量, 但是不去读取测量结果, 那么系统的状态还能够使用之前的公式来描述吗?
如果我们已经知道 $\uparrow$ 的概率为 $W_{\uparrow}$, $\downarrow$ 的概率为 $W_{\downarrow}$. 那么我们可以使用如下标记来示意量子态的叠加:
$$ \epsilon = \left\{|\uparrow\rangle,W_{\uparrow};|\downarrow\rangle, W_{\downarrow}\right\}\\ W_{\uparrow},W_{\downarrow}\geq 0,\quad W_{\uparrow}+W_{\downarrow}=1 $$
- 自旋态合成
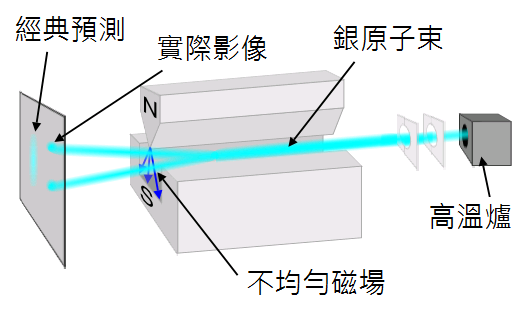
在使用磁场区分出电子的自旋前, 如何描述原子束的自旋态? 将已经被磁场分离的两种原子束合并, 又应该如何表述自旋态?
假设一个量子系统由两个自旋合成: $$ |\Psi\rangle = \frac{1}{\sqrt{2}}\left(|\uparrow\uparrow\rangle + |\downarrow\downarrow\rangle\right) $$ 那么如何描述第一个自旋的状态?
设测量第一个自旋子系统的算符为 $\hat{R}$, 那么测量平均值为
$$ \langle\hat{R}\rangle = \langle\psi|\hat{R}|\psi\rangle = \frac{1}{2}\langle\uparrow\uparrow|\hat{R}|\uparrow\uparrow\rangle + \frac{1}{2}\langle\downarrow\downarrow|\hat{R}|\downarrow\downarrow\rangle $$
$\hat{R}$ 只能作用在第一个自旋上, 所以就有
$$ \begin{aligned} \langle\hat{R}\rangle &= \langle\psi|\hat{R}|\psi\rangle = \frac{1}{2}\langle\uparrow|\hat{R}|\uparrow\rangle + \frac{1}{2}\langle\downarrow|\hat{R}|\downarrow\rangle \\ &= \text{Tr}\left[\left(\frac{1}{2}|\uparrow\rangle\langle\uparrow| + \frac{1}{2}|\downarrow\rangle\langle\downarrow|\right)\hat{R}\right]\\ &= \text{Tr}\left(\hat{\rho}\hat{R}\right) \end{aligned} $$
$\hat{\rho}$ 是第一个自旋的密度矩阵:
$$ \frac{1}{2}|\uparrow\rangle\langle\uparrow| + \frac{1}{2}|\downarrow\rangle\langle\downarrow| $$
量子系综
我们将问题 $1$ 中的讨论拓展至更一般的情形:
$$ \epsilon = \left\{|\psi_{\alpha}\rangle, W_{\alpha}; \alpha = 1,2,\dots\right\} $$
这样的"以概率 $W_{\alpha}$ 处于态 $|\psi_{\alpha}\rangle$ 的系统"便是量子系综, 它是 Hilbert Space 中的一个经典概率分布.
问题 $2$ 中的情形其实和问题 $1$ 一样.
应当注意的是, 在上述的系综构造过程中, 我们从未假定量子态 $\{|\psi_{\alpha}\rangle\}$ 需要彼此正交. 如果说 $|\psi\rangle$ 是由第 $\alpha$ 个实验制备的, 不同的实验之间也不需要有什么关系. 比如:
$$ \epsilon = \{|\uparrow\rangle, W_{\uparrow};|\rightarrow\rangle,W_{\rightarrow\rangle}\} $$
系综中的测量
若有物理量算符 $\hat{R}$, 则其在系综中测量得到 $r_{k}$ 的概率为
$$ P_{k} = \langle\psi|\hat{\pi}_{k}|\psi\rangle = \sum_{\alpha}W_{\alpha}\langle\psi_{\alpha}|\hat{\pi}_{k}|\psi_{\alpha}\rangle $$
所以物理量 $\hat{R}$ 的平均值为
$$ \begin{aligned} \langle\hat{R}\rangle_{\psi} &= \sum_{k}r_{k}P_{k} = \sum_{\alpha}W_{\alpha}\langle\psi_{\alpha}|\sum_{k}r_{k}\hat{\pi}_{k}|\psi_{\alpha}\rangle\\ &= \sum_{\alpha}W_{\alpha}\langle\psi_{\alpha}|\hat{R}|\psi_{\alpha}\rangle \end{aligned} $$
这里我们另外引进一组正交归一基 $\{|n\rangle\}, (n = 0,1,\dots)$, 那么就可以将物理量算符写作这一组基的展开形式:
$$ \hat{R} = \sum_{n}\color{red}{c_{n}}|n\rangle = \sum_{n}|n\rangle\color{red}{\langle n|\hat{R}} $$
所以原本的平均值可以写作
$$ \begin{aligned} \langle\hat{R}\rangle_{\psi} &= \sum_{\alpha}W_{\alpha}\langle\psi_{\alpha}|\hat{R}|\psi_{\alpha}\rangle\\ &= \sum_{\alpha}W_{\alpha}\langle\psi_{\alpha}|\sum_{n}|n\rangle\langle n|\hat{R}|\psi_{\alpha}\rangle\\ &= \sum_{n}\langle n|\left\{\hat{R}\sum_{\alpha}|\psi_{\alpha}\rangle W_{\alpha}\langle\psi_{\alpha}|\right\}|n\rangle\\ &= \text{Tr}\left\{\hat{R}\color{red}{\sum_{\alpha}|\psi_{\alpha}\rangle W_{\alpha}\langle\psi_{\alpha}|}\right\} \end{aligned} $$
所以我们就可以引入密度矩阵:
$$ \hat{\rho} = \sum_{\alpha}|\psi_{\alpha}\rangle W_{\alpha}\langle\psi_{\alpha}| $$
所以测量概率 $P_{k}$ 和平均值 $\langle R\rangle$ 就可以由密度矩阵来导出:
$$ P_{k} = \text{Tr}(\hat{\rho}\hat{\pi}_{k}),\quad\langle R\rangle = \text{Tr}(\hat{\rho}\hat{R}) $$
既然平均值已经可以导出, 则平均值的涨落, 也就是方差也可以导出
$$ \text{Var}(\hat{A}) = \langle\hat{A}^{2}\rangle - \langle\hat{A}\rangle^{2} = \text{Tr}\left(\hat{\rho}\hat{A}^{2}\right) - \left[\text{Tr}\left(\hat{\rho}\hat{A}\right)\right]^{2} $$
密度矩阵的性质
- 厄密性
$$ \hat{\rho} = \hat{\rho}^{\dagger} $$
- 正定性
$$ \forall |\psi\rangle, \langle\psi|\hat{\rho}|\psi\rangle\geq 0 $$
- 归一性
$$ \text{Tr}\left(\hat{\rho}\right) = \sum_{\alpha}W_{\alpha} = 1 $$
子系统
若一个量子系统由两个子系统 $A,B$ 组成, 则其量子态可以写作
$$ |\Psi\rangle = \sum_{ij}c_{ij}|\psi_{i}^{(A)}\rangle|\phi_{j}^{(B)}\rangle $$
$\{|\psi_{i}^{(A)}\rangle\},\{|\phi_{j}^{(B)}\rangle\}$ 分别是子系统 $A,B$ 的正交归一完备基.
所以对子系统 $A$ 的物理量算符 $\hat{R}^{(A)}$ 的平均值为
$$ \begin{aligned} \langle\hat{R}^{(A)}\rangle &= \langle\Psi|\hat{R}^{(A)}|\Psi\rangle = \left(\sum_{i’j’}c^{*}_{i’j’}\langle\phi_{j’}^{(B)}|\langle\psi_{i’}^{(A)}|\right)\hat{R}^{(A)}\left(\sum_{ij}c_{ij}|\psi_{i}^{(A)}|\phi_{j}^{(B)}\rangle\right)\\ &= \sum_{ijk}c_{ij}^{*}c_{kj}^{ }\langle\psi_{i}^{(A)}|\hat{R}^{(A)}|\psi_{j}^{(A)}\rangle = \boxed{\text{Tr}\left(\hat{\rho}^{(A)}\hat{R}^{(A)}\right)} \end{aligned} $$
$\hat{\rho}^{(A)}$ 是子系统 $A$ 的密度矩阵. $$ \hat{\rho}^{(A)} = \text{Tr}_{B}(|\Psi\rangle\langle\Psi|) = \sum_{i,k}\sum_{j}c_{ij}c_{kj}^{*}|\psi_{i}^{(A)}\rangle\langle\psi_{k}^{(A)}| $$
因为我们只关心子系统 $A$ 的物理量 $\hat{R}^{(A)}$, 所以系统的状态可以用所标记公式表示.
在问题 $1$ 中, 我们可以将自旋和宇宙看作两个子系统, 那么自旋和宇宙总系统的量子态可以写作
$$ \Psi\rangle = |\uparrow\rangle|\Phi_{\uparrow}\rangle + |\downarrow\rangle|\Phi_{\downarrow}\rangle $$
$|\Phi_{\uparrow}\rangle, |\Phi_{\downarrow}\rangle$ 是自旋以外的整个宇宙的量子态. 这里我们没有添加归一化的假设; 并且因为宇宙各部分相互作用如此复杂, 以至于我们可以相当有信心地认为, $|\Phi_{\uparrow}\rangle, |\Phi_{\downarrow}\rangle$ 是正交的.
综上所述, 如果系统 $A$ 是大系统 $A\oplus B$ 的子系统, 并且 $A\oplus B$ 可以用确定的 Hilbert Space 中的矢量来表示, 那么 $A$ 不能用 Hilbert Space 中的矢量来表示, 而是应该使用密度矩阵来进行描述.
冯·诺依曼定理
Lemma
若 $E(\hat{R})$ 是厄密算符 $\hat{R}$ 的函数, 且具有以下性质:
- 归一性: $E(\hat{I}) = 1$;
- 正定性: $\forall \hat{\pi}, E(\pi)\geq 0$;
- 线性性: $E(\sum_{i}c_{i}\hat{R}_{i}) = \sum_{i}c_{i}E(\hat{R}_{i})$.
则存在密度矩阵 $\hat{\rho}$, 使得 $\forall \hat{R}, E(\hat{R}) = \text{Tr}\left(\hat{\rho}\hat{R}\right)$.
Hilbert Space 中的矢量 $|\psi\rangle$ 实际上也对应一个密度矩阵 $|\psi\rangle\langle\psi|$, 即其投影算符 $\hat{\pi}_{\psi}$. 而为了区分密度矩阵和 Hilbert Space 中矢量表示的状态, 我们将前者称为混合态, 后者称为纯态.
密度矩阵可以使用纯态来展开. 因为 $\hat{\rho}$ 是存在于 Hilbert Space 上的厄米算符, 所以其本征矢量可以构成一组基用于展开:
$$ \hat{\rho} = \sum_{n}p_{n}|n\rangle\langle n|,\quad\langle n|m\rangle = \delta_{mn} $$
$p_{n}$ 的性质
- 厄密性: $p_{n}^{*} = p_{n}$;
- 正定性: $p_{n}\geq 0$;
- 归一性: $\sum_{n}p_{n} = 1$.
如果不对纯态做出正交性要求, 那么对于一个已知的密度矩阵 $\hat{\rho}$, 可以有多种分解方式, 即
$$ \hat{\rho} = \sum_{\alpha = 1}^{M}W_{\alpha}|\psi_{\alpha}\rangle\langle\psi_{\alpha}| = \sum_{i = 1}^{N}W_{i}’|\phi_{i}\rangle\langle\phi_{i}| $$
$W_{\alpha}, W_{i}’$ 是概率, 且满足归一性: $$ \sum_{\alpha}W_{\alpha} = \sum_{i}W_{i}’ = 1 $$
我们验证一般情况下密度矩阵的幂等性:
$$ \hat{\rho}^{2} = \left(\sum_{\alpha}p_{\alpha}|\psi_{\alpha}\rangle\langle\psi_{\alpha}|\right)\left(\sum_{\beta}p_{\beta}|\psi_{\beta}\rangle\langle\psi_{\beta}|\right) = \sum_{\alpha}p_{\alpha}^{2}|\psi_{\alpha}\rangle\langle\psi_{\alpha}| $$
所以, 如果要出现幂等性, 即 $\hat{\rho}^{2} = \hat{\rho}$, 就要求 $p_{n}^{2} = p_{n}$, 即 $p_{n} = 0, 1$. 这个条件只有在 $\hat{\rho} = |\psi\rangle\langle\psi|$, 也就是 $\hat{\rho}$ 是纯态的情形下才成立.
所以也有
Lemma
$\hat{\rho}$ 是纯态 $\Longleftrightarrow\hat{\rho}^{2} = \hat{\rho}$.
布洛赫球(Bloch Sphere)
如果 $\hat{\rho}_{1}, \hat{\rho}_{2}$ 是密度矩阵, 引入参数 $\lambda\in[0, 1]$, 则 $\hat{\rho} = \lambda\hat{\rho}_{1} + (1 - \lambda)\hat{\rho}_{2}$ 也是密度矩阵.
一个纯态无法使用与之不同的密度矩阵的线性组合(被称作 “凸组合”)表示, 这种性质可以理解为 “纯态在密度矩阵张成空间的边界上”.
考虑一个 $\frac{1}{2}$ 单自旋子, 则 $\hat{s}_{z}$ 的本征态可以张成 $2\times 2$ 的密度矩阵. 我们选择单位矩阵和泡利矩阵作为基底:
$$ \forall\hat{A},\quad\hat{A} = \frac{1}{2}\left(a_{0}\hat{I} + a_{1}\hat{\sigma}_{x} + a_{2}\hat{\sigma}_{y} + a_{3}\hat{\sigma}_{z}\right) = \frac{1}{2}\left(a_{0}\hat{I} + \mathbf{a}\cdot\hat{\mathbf{\sigma}}\right) $$
$\mathbf{a} = (a_{1},a_{2},a_{3})$ 为矢量, $\hat{\mathbf{\sigma}} = \left(\hat{\sigma}_{x},\hat{\sigma}_{y},\hat{\sigma}_{z}\right)$ 是由泡利矩阵组成的矢量. 因为泡利矩阵都是无迹的, 所以有
$$ \text{Tr}\left(\hat{A}\right) = \frac{1}{2}\cdot 2\cdot a_{0} = a_{0} $$
对于密度矩阵 $\hat{\rho}$, 则 $a_{0} = 1$. 即有
$$ \hat{\rho} = \frac{1}{2}\left(\hat{I} + |\mathbf{a}|\hat{\mathbf{a}}\cdot\hat{\mathbf{\sigma}}\right) $$
$\hat{\mathbf{a}}$ 是 $\mathbf{a}$ 的方向矢量, 所以 $\hat{\mathbf{a}}\cdot\hat{\mathbf{\sigma}}$ 是自旋在 $\hat{\mathbf{a}}$ 方向上的投影, 其本征方程为 $$ \hat{\mathbf{a}}\cdot\hat{\mathbf{\sigma}}|\pm\mathbf{n}\rangle = \pm\frac{1}{2}|\pm\mathbf{n}\rangle $$
所以 $\hat{\rho}$ 的本征值为 $\frac{1}{2}\pm \frac{|\mathbf{a}|}{2}$. 为了保持其正定性, 需要有
$$ |\mathbf{a}|\leq 1 $$
也就是说, 所有的密度矩阵在 $\mathbf{a}$ 空间中组成了一个球, 被称作布洛赫球(Bloch Sphere). 球中心即为
$$ \hat{\rho}_{0} = \frac{1}{2}\hat{I} $$
这是各向同性的混合态, 也是熵极大态. 而球的表面上, 即
$$ \hat{\rho} = \frac{1}{2}\left(\hat{I} + \mathbf{n}\cdot\hat{\mathbf{\sigma}} \right) = |\mathbf{n}\rangle\langle\mathbf{n}| $$
本征值为 $1,0$, 本征态为 $|\mathbf{n}\rangle,|-\mathbf{n}\rangle$, 对应于纯态 $|\mathbf{n}\rangle$.
这就是前面所说的纯态的密度矩阵在布洛赫球的边界的含义.