布洛赫和

紧束缚近似假定电子受到了很强的束缚作用. 当电子靠近原子实, 将其所在势场近似为库伦势. 因此电子在原子实附近的行为于类氢原子的轨道波函数将会有相似性.

至于其它原子实对电子的作用将被处理为微扰. 原本的轨道波函数是分立的, 引入其它原子实的势场微扰就会使能级产生劈裂.

我们假定电子的束缚态波函数为 $\phi_{i}(\vec{r})$, 写出含势场的薛定谔方程:

$$ \left[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r}-\vec{R_m})\right]\phi_{i}(\vec{r}-\vec{R_m})=\epsilon_{i}\phi_{i}(\vec{r}-\vec{R_m}) $$

根据已经学到的量子力学的知识, 对于一个核外电子的波函数, 我们知道其可以为 $s$ , $p$ 轨道波函数, 在不考虑自旋的情况下则是由 $n, l, m$ 三个量子数来描述.

而真正的周期性势场 $U(\vec{r})$ 与 $V(\vec{r})$ 是有区别的. 所以我们将其差异部分, 也就是 $U(\vec{r}) - V(\vec{r} - \vec{R_m})$ 视为微扰哈密顿量. 那么就有对波函数 $\psi(\vec{r})$ :

$$ \left[-\frac{\hbar^2}{2m}\nabla^2+U(\vec{r})\right]\psi(\vec{r})=E\psi(\vec{r}) $$

对于不同的格点, 有着不同的势场 $V(\vec{r}-\vec{R_m})$ ($m = 1,\dots, N$). 所以这会产生 $N$ 个解 $\phi_{i}(\vec{r}-\vec{R_m})$. 我们假定在周期性势场下, 电子的波函数即为这 $N$ 个束缚态波函数的线性叠加:

$$ \psi(\vec{r}) = \sum_{m}a_{m}\phi_{i}(\vec{r}-\vec{R_m}) $$

将其带入到 $\psi$ 的薛定谔方程中, 即有:

$$ \sum_{m}\left[\epsilon_{i}+(U(\vec{r})-V(\vec{r}-\vec{R_m}))a_{m}\phi_{i}(\vec{r}-\vec{R_m})\right] = E\sum_m a_{m}\phi_{i}(\vec{r}-\vec{R_m}). $$

并且我们将这些不同格点处的束缚态波函数视为线性无关的, 即近似正交归一的. 所以对上式等号的左右两边都对 $\phi_{i}(\vec{r}-\vec{R_m})$ 做内积(相当于都左乘 $\int d^3\vec{r}\phi_{i}^{*}(\vec{r}-\vec{R_m})$), 就有:

$$ \sum_{m}a_m\int d^3\vec{r}\phi_{i}^{*}(\vec{r}-\vec{R_n})(U(\vec{r})-V(\vec{r}-\vec{R_m}))\phi_{i}(\vec{r}-\vec{R_m}) = a_{n}(E-\epsilon_{i}) $$

因为我们假定了这些波函数是正交归一的, 所以 $$\int d^3\vec{r}\phi_{i}^{*}(\vec{r}-\vec{R_n})\phi_{i}(\vec{r}-\vec{R_m}) = \delta_{nm}, $$ 所以求和项中只有 $n$ 会被保留下来.

换元 $\vec{\zeta} = \vec{r} - \vec{R_m}$, 将上式简写为以下形式:

$$ \sum_{m}a_m\int d^3\zeta\phi_{i}^{*}\left(\zeta-(\vec{R_n}-\vec{R_m})\right) \left(U(\zeta)-V(\zeta) \right) \phi_{i}(\zeta)\\ =-\sum_{m}a_{m}J(\vec{R_n}-\vec{R_m}) = a_{n}(E-\epsilon_{i}) $$

$$\int d^3\zeta\phi_{i}^{*}(\zeta-\vec{R})\left(U(\zeta)-V(\zeta)\right)\phi_{i}(\zeta)=-J(\vec{R})$$

$J$ 被称为 交叠积分(或者重叠积分), 这是因为只有当 $\phi_{i}(\vec{R_n})$ 和 $\phi_{i}(\vec{R_m})$ 存在共同分量(即并非完全正交)时, 该量才不会等于 $0$ .

对于具有周期性边界条件的晶体, 我们不仅能推测 $J(\vec{R_n}-\vec{R_m})$ 只和格点 $n$ 和 $m$ 的相对位置有关, 还可以猜测系数 $a_{m}$ 具有平面波的形式.即

$$ a_{m} = Ce^{i\vec{k}\cdot\vec{R_m}}, $$

代入到前面我们做内积的式子中, 即有

$$ -C\sum_{m}J(\vec{R_n}-\vec{R_m})e^{-i\vec{k}\cdot(\vec{R_n}-\vec{R_m})} = C(E-\epsilon_{i})e^{i\vec{k}\cdot(\vec{R_n}-\vec{R_m})} = C(E - \epsilon_{i}) $$

同样是利用周期性边界条件, 我们将 $\vec{R_n} - \vec{R_m}$ 进行换元, 即有

$$ E(\vec{k}) = \epsilon_{i} - \sum_{s}J(\vec{R_s})e^{-i\vec{k}\cdot\vec{R_s}} $$

$\vec{R_s} = \vec{R_n} - \vec{R_m}$

对于波函数则可以写作为布洛赫和的形式:

$$ \psi_{\vec{k}}(\vec{r}) = \frac{1}{\sqrt{N}}\sum_{m}e^{i\vec{k}\cdot\vec{R_m}}\phi_{i}^{\vec{r}-\vec{R_m}}=e^{i\vec{k}\cdot\vec{r}}\left(\frac{1}{\sqrt{N}}\sum_{s}r^{-i\vec{k}\cdot\vec{R_s}}\phi_{i}(\vec{R_s})\right) $$

$\frac{1}{\sqrt{N}}$ 是归一化因子

能带计算

一维晶格

如果我们要计算$s$轨道波函数的布洛赫和, 只考虑最近邻(nearest neighbours)格点的交叠函数, 我们会有

$$ E(\vec{k}) = \epsilon_{s} - J_{0} - J_{1}e^{-ika} - J_{1}e^{ika} $$

一般 $U - V < 0$, 所以 $J > 0$. 以此将上式简化

$$ E = \epsilon_{s} - J_{0} - 2J\cos(ka) $$

$a$ 为晶格常数.

二次量子化下的紧束缚模型

考虑一维的原子链, 每个原胞一个原子, 每个原子附近一个电子. $$ \hat{H} = -\sum_{ij}(t_{ij}\hat{c_{i}^{\dagger}}\hat{c_{j}}+t_{ji}\hat{c_{j}^{\dagger}}\hat{c_{i}}) + \sum_{i}V_{i}\hat{c_{i}^{\dagger}}\hat{c_{i}} $$

第一个 $\sum$ 代表的是跃迁(hopping)能, 第二个 $\sum$ 代表的是在位势能, $\hat{c_{i}}^{\dagger}, \hat{c_{i}}$ 分别为产生算符和湮灭算符.

升降算符存在关系: $$ \sum_{i}\hat{c_{i}}^{\dagger}\hat{c_{i}} = \sum_{i}\hat{n_{i}} = N $$

$N$ 为总粒子数

则有 $$ \hat{H} = -\sum_{ij}(t_{ij}\hat{c_{i}}^{\dagger}\hat{c_{j}}+h.c.)+ VN $$

h.c. = Hermitian Conjugate, 意为’厄米共轭'

若原子等距排列且只考虑最近邻跃迁能, 则将哈密顿量简化为:

$$ \hat{H} = -t\sum_{i}(\hat{c_{i}}^{\dagger}\hat{c_{i+1}}+h.c.) $$ 这就是二次量子化表述的紧束缚模型近似下的哈密顿量.

更具体一点的计算, 就是使用傅里叶变换写出 $k$ 表象下的哈密顿量:

$$ \hat{c_{j}} = \frac{1}{\sqrt{N}}\sum_{k}e^{ikx_{j}} $$ 代入到原哈密顿量的式子中即有 $$ \hat{H}(k)=-t\sum_{k}(\hat{c_{k}}^{\dagger}\hat{c_{k}}+h.c.)=\sum_{k}(-2t\cos{(ka)}\hat{c_{k}}^{\dagger}\hat{c_{k}}) $$ 所以就有了 $$ E(k) = -2t\cos{(ka)} $$

二维晶格

简单正方晶格

$$ E = \epsilon - 2t\left(\cos(k_{x}a) + \cos(k_{y}a)\right) $$

二维六角晶格(最密堆积)

二维六角晶格的经典代表就是石墨烯和六方氮化硼. 简单起见我们先考虑相同原子的石墨烯二维结构.

紧束缚模型要求仅考虑最近邻原子, 那么我们写出满足要求的哈密顿量为:

$$ \hat{H} = t\sum_{i, j = \langle i\rangle}a_{i}^{\dagger}b_{j} + h.c.. $$

$a_{i}, a_{i}^{\dagger}$是 $A$ 处的湮灭, 产生算符, 而 $b_{i}, b_{i}^\dagger$ 同理. ‘$i,j = \langle i\rangle$’ 是表达最近邻的意思.

哈密顿量可以用三种方法表示(Dirac Bra-Ket, Ascending and Descending Operators, Field Operators). 其中第二种和第三种在某些情况下其实是等同的.详情见于哈密顿量的三种形式.

在石墨烯原胞中, 包含着两个不等价的碳原子, 我们将晶格基矢选为

$$ \vec{a_{1}}=\left(\frac{3}{2}, \frac{\sqrt{3}}{2}\right)a,\\ \vec{a_{2}}=\left(\frac{3}{2},-\frac{\sqrt{3}}{2}\right)a. $$

$a$ 为晶格常数

二维空间中计算倒格子基矢的方法和三维空间中的一样, 只是需要我们构造出一个辅助矢量 $\vec{a_{3}} = \vec{a_{1}}\times \vec{a_{2}}$, 代入到传统的求倒格子公式中即可. 由此我们得到二维下的倒格子基矢:

$$ \vec{b_{1}}=\frac{1}{a}\left(\frac{2\pi}{3}, \frac{2\sqrt{3}}{3}\right),\\ \vec{b_{2}}=\frac{1}{a}\left(\frac{2\pi}{3},-\frac{2\sqrt{3}}{3}\right). $$

原子到最近邻原子之间的距离分别为

$$ \vec{\delta_{1}} = \left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)a,\\ \vec{\delta_{2}} = \left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)a,\\ \vec{\delta_{3}} = \left(0 , -1\right)a. $$

Bloch 态和 Wannier 态之间呈现为 Fourier 变换关系:

$$ \psi_{nl}(r) = \frac{1}{\sqrt{N}}\sum_{l}e^{ik\cdot l}W_{n}(r,l) $$

$W_{n}(r,l)$ 是关于 $(r-l)$ 的 Wannier 函数. 关于 Wannier 函数的详细内容, 见于Wannier函数.

先不考虑存在多条能带, 所以我们将能带指标的 $n$ 忽略.

而又因为一个原胞中存在着两个不等价的碳原子, 所以我们赋给每个碳原子一个Bloch态

$$ \varphi_{1}=\frac{1}{\sqrt{N}}\sum_{l}e^{i\vec{k}\cdot\vec{R_{l}^{A}}}\phi(\vec{r}-\vec{R_{l}^{A}}),\\ \varphi_{2}=\frac{1}{\sqrt{N}}\sum_{l}e^{i\vec{k}\cdot\vec{R_{l}^{B}}}\phi(\vec{r}-\vec{R_{l}^{B}}). $$

$N$ 是体系中原胞总数, $\vec{R_{l}^{A}}$ 和 $\vec{R_{l}^{B}}$ 分别代表原胞中两个不等价碳原子的位置.

在这里我们使用了原子轨道波函数 $\phi$ 来近似代替局域内的 Wannier 函数 $W$. 这是因为在这里我们只考虑最近邻原子的交叠函数, 所以这两个函数的差异并不大.

所以系统的波函数就可以写作布洛赫态的线性组合

$$ \psi(\vec{r})=c_{1}\varphi_{1} + c_{2}\varphi_{2} = \frac{c_{1}}{\sqrt{N}}\sum_{l}e^{i\vec{k}\cdot\vec{R_{l}^{A}}}\phi(\vec{r}-\vec{R_{l}^{A}}) + \frac{c_{2}}{\sqrt{N}}\sum_{l’}e^{i\vec{k}\cdot\vec{R_{l’}^{B}}}\phi(\vec{r}-\vec{R_{l’}^{B}})\\ =\frac{1}{\sqrt{N}}\sum_{l,l’}\left[e^{i\vec{k}\cdot\vec{R_{l}^{A}}}c_{1}\phi(\vec{r}-\vec{R_{l}^{A}})+e^{i\vec{k}\cdot\vec{R_{l’}^{B}}}c_{2}\phi(\vec{r}-\vec{R_{l’}^{B}})\right] $$

为了得到能量本征值, 我们就需要求解本征方程:

$$ \hat{H}|\psi\rangle = E|\psi\rangle $$

因为我们采用的近似波函数 $\varphi$ 满足正交关系

$$ \langle\varphi_{i}|\varphi_{j}\rangle=\delta_{ij} $$

所以我们将本征方程整理为

$$ (\hat{H}-E)|\psi\rangle = 0|\psi\rangle $$

从而化为久期方程

$$ \left|\begin{array}{c} H_{11} - E & H_{12} \\ H_{21} & H_{22} - E \\ \end{array}\right|=0 $$

$H_{ij}=\langle\varphi_{i}|\hat{H}|\varphi_{j}\rangle, H_{12} = H_{21}^{*}$

这是一个关于 $E$ 的二次方程, 解出 $E$ 的形式解:

$$ E = \frac{1}{2}\left[H_{11}+H_{22}\pm\sqrt{(H_{11}-H_{22})^2+4|H_{12}|^2}\right] $$

所以问题就转换为了计算矩阵元 $H_{ij}$ 的具体值.

$$ H_{11} = \langle\varphi_{1}|\hat{H}|\varphi_{1}\rangle = \frac{1}{N}\sum_{l,l’}e^{-i\vec{k}\cdot(\vec{R_{l}^{A}}-\vec{R_{l’}^{A}})}\langle\phi(\vec{r}-\vec{R_{l}^{A}})|\hat{H}|\phi(\vec{r}-\vec{R_{l’}^{A}})\rangle $$

原子轨道波函数 $\varphi$ 的正交性有 $$ \langle\phi(\vec{r}-\vec{R_{l}^{A}})|\hat{H}|\phi(\vec{r}-\vec{R_{l’}^{A}})\rangle = \epsilon_{1}\langle\phi(\vec{r}-\vec{R_{l}^{A}})|\hat{H}|\phi(\vec{r}-\vec{R_{l’}^{A}})\rangle = \epsilon_{1}\\ \delta(\vec{R_{l}^{A}}-\vec{R_{l’}^{A}}) = \frac{1}{N}\sum_{l,l’}e^{-i\vec{k}\cdot(\vec{R_{l}^{A}}-\vec{R_{l’}^{A}})} $$

同理, 我们对 $H_{22}$ 可以求出

$$ H_{22} = \langle\varphi_{2}|\hat{H}|\varphi_{2}\rangle = \frac{1}{N}\sum_{l,l’}e^{-i\vec{k}\cdot(\vec{R_{l}^{B}}-\vec{R_{l’}^{B}})}\langle\phi(\vec{r}-\vec{R_{l}^{B}})|\hat{H}|\phi(\vec{r}-\vec{R_{l’}^{B}})\rangle = \epsilon_{2} $$

而对于交叉项我们有

$$ H_{12}=\langle\varphi_{1}|\hat{H}|\varphi_{2}\rangle = \frac{1}{N}\sum_{l,l’}e^{i\vec{k}\cdot(\vec{R_{l}^{B}}-\vec{R_{l’}^{A}})}\langle\phi(\vec{r}-\vec{R_{l}^{B}})|\hat{H}|\phi(\vec{r}-\vec{R_{l’}^{A}})\rangle\\ =\frac{1}{N}\sum_{l,l’}Je^{i\vec{k}\cdot(\vec{R_{l}^{B}}-\vec{R_{l’}^{A}})} $$

$J = \langle\phi(\vec{r}-\vec{R_{l}^{B}})|\hat{H}|\phi(\vec{r}-\vec{R_{l’}^{A}})\rangle$, 这就是我们前面所介绍的交叠积分.

而对于哈密顿量, 我们将其写作 $$ \hat{H} = \hat{H_{a}} + V - v_{a} $$

$\hat{H_{a}}$ 是原子的哈密顿量, $V$ 是晶格势, $v_{a}$ 是原子势.

对于 $\hat{H_a}$, 有 $$ \langle\phi(\vec{r}-\vec{R_{l}^{B}})|\hat{H_{a}}|\phi(\vec{r}-\vec{R_{l’}^{A}})\rangle = \epsilon_{1}\langle\phi(\vec{r}-\vec{R_{l}^{B}})|\phi(\vec{r}-\vec{R_{l’}^{A}})\rangle = \epsilon_{1}\delta_{AB}\delta_{l,l’} $$ 所以我们就有

$$ J = \langle\phi(\vec{r}-\vec{R_{l}^{B}})|(V-v_a)|\phi(\vec{r}-\vec{R_{l’}^{A}})\rangle $$

因为我们考虑的是紧束缚模型, 即仅考虑最近邻原子的跃迁方向, 即有

$$ |\vec{R_{l}^{A}}-\vec{R_{l’}^{B}}|=|\delta_{i}| $$

$\delta_{i}$ 即为最近邻原子的位移矢量: $$ \vec{\delta_{1}} = \left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)a, \vec{\delta_{2}} = \left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)a, \vec{\delta_{3}} = \left(0 , -1\right)a. $$

于是就有

$$ H_{12} = \frac{1}{N}\sum_{l,l’}e^{i\vec{k}\cdot(\vec{R_{l}^{A}}-\vec{R_{l’}^{B}})}J=\frac{1}{N}(e^{i\vec{k}\cdot\vec{\delta_{1}}}+e^{i\vec{k}\cdot\vec{\delta_{2}}}+e^{i\vec{k}\cdot\vec{\delta_{3}}})NJ\\ =J\left[e^{-ik_{y}\cdot a}+2\cos{k_{y}\left(\frac{\sqrt{3}a}{2}\right)\cdot e^{ik_{x}\cdot\frac{a}{2}}}\right] $$

于是将各矩阵元代入到二次方程的解中, 就有

$$ E(\vec{k}) = \epsilon_{1}\pm J\sqrt{3+2\cos{(\sqrt{3}k_{y}a)}+4\cos{\left(\frac{\sqrt{3}k_{y}a}{2}\right)}\cos{\left(\frac{3k_{x}a}{2}\right)}} $$

我们可以通过简单的二维格点将其绘制出来.

% 定义常数
a = 1; % 石墨烯晶格常数
t = 1; % 能带结构参数
kx = linspace(-pi/a,pi/a,200); % kx空间路径
ky = linspace(-pi/a,pi/a,200); % ky空间路径
[kx,ky] = meshgrid(kx,ky);

% 计算能带
E1 = t*sqrt(3+2*cos(sqrt(3)*kx*a)+4*cos(sqrt(3)/2*kx*a).*cos(3/2*ky*a)); % 第一条能带
E2 = -E1; % 第二条能带

% 绘制能带图
figure;
h1 = surf(kx,ky,E1,'edgecolor','none'); hold on;
h2 = surf(kx,ky,E2,'edgecolor','none');
xlabel('k_x','fontsize',14);
ylabel('k_y','fontsize',14);
zlabel('E','fontsize',14);
title('能带结构','fontsize',16);
set(gca,'fontsize',14,'linewidth',2);
view([30 30]);

% 绘制colorbar
hcb = colorbar;
set(hcb,'position',[0.9 0.15 0.03 0.7],'fontsize',14,'linewidth',2);
colormap(jet); % 设置colorbar颜色

% 调整每个surface对象的颜色数据范围
caxis(h1,[-4 4]);
caxis(h2,[-4 4]);

% 调整z轴的显示范围，使两个能带大小一致
zlim([-4 4]);

如果你没有本地安装 Matlab, 你可以尝试注册 Matlab 账号并且在 Matlab Online 中执行代码.

运行代码得到的效果如下:

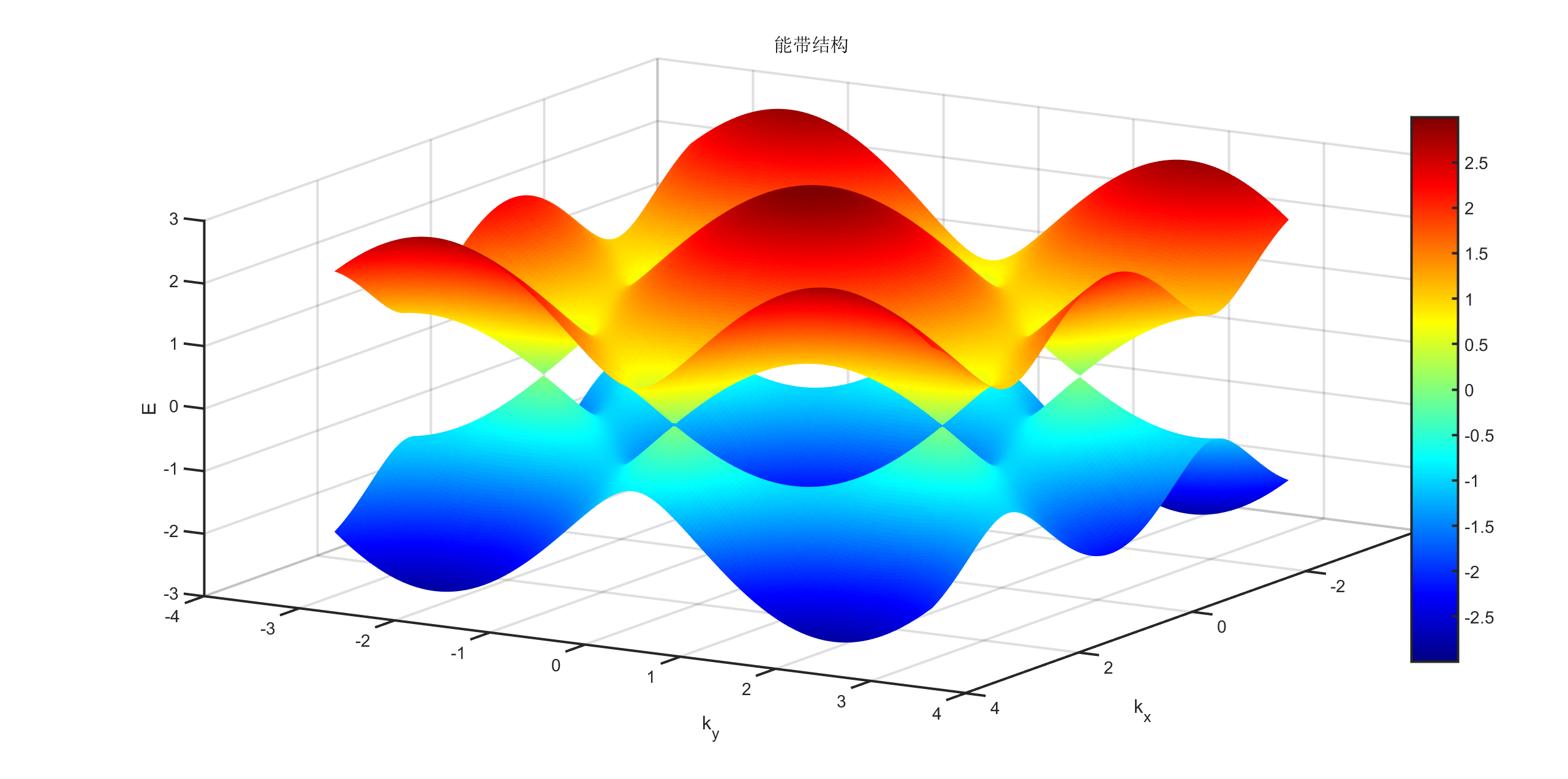
可以看到 $E = 0$ 的几个相对锥, 我们称其为狄拉克锥, 锥的顶点被称为狄拉克点. 有关于如何打开狄拉克点的能隙的内容, 具体见于Twisted-Bilayer-Graphene

从上图可以看到两面能带在 $K$ 和 $K’$ 相交, 正是上面所说的狄拉克点. 我们引入波矢差 $\vec{q} = \vec{k} - \vec{K}$, 以此来展开狄拉克点附近的哈密顿量.

正如"狄拉克锥"的名字那样, 狄拉克点附近的石墨烯电子结构可以被近似处理为线性色散关系

那么我们就可以得到这样的哈密顿量的描述方式:

$$ h_{\vec{K}}(\vec{q})\approx\hbar v_{F} \begin{bmatrix} 0 & q_{x} - iq_{y} \\ q_{x} + iq_{y} & 0 \\ \end{bmatrix} =\hbar v_{F}\sigma\cdot\vec{q} $$

$v_{F} = \frac{3ta}{2}$, 石墨烯中的等效费米速度.

有关于哈密顿量和泡利矩阵矩阵更详细的关系.

三维晶格

简单立方堆积($sc$)

求 $s$ 态. 我们不难推测: 该波函数 $\phi_{s}(\vec{r})$ 是球对称的.

而 $sc$ 中最近邻原子有 $6$ 个, 且距离为 $a$. 那么它们共享同一个交叠积分 $J_1$.

又因为 $s$ 态波具有偶宇称 $\phi_{s}(\vec{r}) = \phi_{s}(-\vec{r})$, 因此有 $J_{1} > 0$.

将最近邻格式 $(\pm a,0,0), (0,\pm a,0), (0,0,\pm)$ 代入到交叠积分表达式中, 即有:

$$ \epsilon(\vec{k}) = \epsilon_{s} - J_{0} - 2J_{1}(\cos{k_{x}a}+\cos{k_{y}a}+\cos{k_{z}a}) $$

由此可知 $\epsilon_{s}$ 被扩展为 $2*2*(1+1+1)J_{1} = 12J_{1}$ 带宽的能带.

体心立方堆积($bcc$)

$$ \epsilon(\vec{k}) = -\alpha - 8\gamma\cos{\left(\frac{1}{2}k_{x}a\right)}\cos{\left(\frac{1}{2}k_{y}a\right)}\cos{\left(\frac{1}{2}k_{z}a\right)} $$

面心立方堆积($fcc$)

$$ \epsilon(\vec{k}) = -\alpha - 4\gamma\left[ \cos{\left(\frac{1}{2}k_{y}a\right)}\cos{\left(\frac{1}{2}k_{z}a\right)}+ \cos{\left(\frac{1}{2}k_{z}a\right)}\cos{\left(\frac{1}{2}k_{x}a\right)}+ \cos{\left(\frac{1}{2}k_{x}a\right)}\cos{\left(\frac{1}{2}k_{y}a\right)} \right] $$

Wannier函数

定义

布洛赫函数本身是关于倒格子点阵的周期函数, 我们可以用下面这个式子描述:

$$ \phi_{\vec{k}}(\vec{r}) = \phi_{\vec{k}+\vec{G}}(\vec{r}) $$

所以将 $\phi_{\vec{k}}(\vec{r})$ 进行傅里叶级数展开:

$$ \phi_{\vec{k}}(\vec{r}) = \frac{1}{\sqrt{N}}\sum_{\vec{R}}a(\vec{R},\vec{r})e^{i\vec{k}\cdot\vec{R}} $$

$a(\vec{R},\vec{r})$ 即为 Wannier 函数.

性质

局域性

$$ \begin{equation} \begin{aligned} a(\vec{R},\vec{r}) & = \frac{1}{\sqrt{N}}\sum_{\vec{k}}e^{-\vec{k}\cdot\vec{r}}\phi_{\vec{k}}(\vec{r})\\ & = \frac{1}{\sqrt{N}}\sum_{\vec{k}}e^{i\vec{k}\cdot(\vec{r}-\vec{R})}u_{\vec{k}}(\vec{r})\\ & = \frac{1}{\sqrt{N}}\sum_{\vec{k}}e^{i\vec{k}\cdot(\vec{r}-\vec{R})}u_{\vec{k}}(\vec{r}-\vec{R})\\ & \Rightarrow a(\vec{R},\vec{r}) = a(\vec{r}-\vec{R}) \end{aligned} \end{equation} $$

所以 Wannier 函数是以正格点为中心的局域函数.

正交性

$$ \begin{aligned} \langle a_{n}(\vec{r}-\vec{R})|a_{n’}(\vec{r}-\vec{R}’)\rangle &=\frac{1}{N}\sum_{\vec{k}}\sum_{\vec{k}’}e^{i\vec{k}\cdot\vec{R}-\vec{k}’\cdot\vec{R}’}\int\phi_{\vec{k}}^{n*}(\vec{r})\phi_{\vec{k}’}^{n’}(\vec{r})\mathrm{d}\vec{r}\\ &= \frac{1}{N}\sum_{\vec{k}}\sum_{\vec{k}’}e^{i(\vec{k}\cdot\vec{R}-\vec{k}’\cdot\vec{R}’)}\delta_{nn’}\delta_{\vec{k}\vec{k}’}\\ &= \frac{1}{N}\sum_{\vec{k}}e^{i\vec{k}\cdot(\vec{R}-\vec{R}’)}\delta_{nn’}\\ &= \delta_{\vec{R}\vec{R}’}\delta_{nn’} \end{aligned} $$

完备性

$$ \sum_{n}\sum_{\vec{R}}a_{n}^{*}(\vec{r}-\vec{R})a_{n}(\vec{r}’-\vec{R}) = \delta_{\vec{r}\vec{r}’} $$

Tight-Binding Model 中的应用

我们简单回顾一下紧束缚模型的一些基本假设和性质:

相邻原子的电子波函数有很小的交叠, 这种交叠导致能带的产生.

适用于内层电子;局域性较强的轨道电子;绝缘体.

非简并情况

$$ \left[-\frac{\hbar^{2}}{2m}\nabla^{2}+V_{\text{atom}}(\vec{r})\right]\varphi = \epsilon\varphi $$

$V_{\text{atom}}(\vec{r})$ 是单原子势场, $\varphi$ 是单原子的总电子波函数.

基于紧束缚模型, 假设真是电子波函数 $\phi$ 是所有格点上孤立原子波函数 $\varphi$ 的线性组合:

$$ \phi(\vec{r}) = \sum_{\vec{R}_{m}}a_{m}\varphi(\vec{r}-\vec{R}_{m}) $$

$\vec{R}_{m}$ 是正格矢.

其中的孤立原子的波函数 $\varphi$ 即为 Wannier 函数.

孤立原子中的电子波函数 $\varphi$ 满足

• 归一性: $\langle\varphi(\vec{r}-\vec{R}_{m})|\varphi(\vec{r}-\vec{R}_{m})\rangle=1$
• (近似)正交性: $\langle\varphi(\vec{r}-\vec{R}_{m})|\varphi(\vec{r}-\vec{R}_{m’})\rangle = 0$

符合 Wannier 函数的基本性质要求.

所以我们就有了

$$ \phi(\vec{r}) = \sum_{\vec{R}_{m}}a_{m}\varphi(\vec{r}-\vec{R}_{m}) $$

并且系数 $\{a_{m}\}$ 需要使得 $\phi(\vec{r})$ 满足

• 布洛赫函数条件

$$ \phi(\vec{r}-\vec{R}_{m}) = e^{i\vec{k}\cdot\vec{R}_{m}}\phi(\vec{r}) $$

• 归一化条件.

$$ a_{m} = \frac{1}{\sqrt{N}}e^{i\vec{k}\cdot\vec{R}_{m}} $$

所以完整的紧束缚近似波函数为

$$ \phi(\vec{r}) = \sum_{\vec{R}_{m}}\frac{1}{\sqrt{N}}e^{i\vec{k}\cdot\vec{R}_{m}}\varphi(\vec{r}-\vec{R}_{m}) $$

将其代入平均场近似下的单电子薛定谔方程:

$$ \left[-\frac{\hbar^{2}}{2m}\nabla^{2}+V(\vec{r})\right]\phi(\vec{r}) = E\phi(\vec{r}) $$

简并情况

$$ \phi(\vec{r}) = \frac{1}{\sqrt{N}}\sum_{\vec{R}_{m}}\sum_{j}e^{i\vec{k}\cdot\vec{R}_{m}}c_{j}\varphi_{j}(\vec{r}-\vec{R}_{m}) $$

非简并复式原胞

石墨烯是一个典型的复式原胞, C 原子经由 $\text{sp}^{2}$ 杂化形成面内夹角为 $120$° 的轨道.

$$ \begin{aligned} &|h_{1}\rangle = \frac{1}{\sqrt{3}}|s\rangle + \frac{\sqrt{2}}{\sqrt{3}}|p_{x}\rangle\\ &|h_{2}\rangle = \frac{1}{\sqrt{3}}|s\rangle - \frac{\sqrt{2}}{\sqrt{3}}\left(\frac{1}{2}|p_{x}\rangle - \frac{\sqrt{3}}{2}|p_{y}\rangle\right)\\ &|h_{3}\rangle = \frac{1}{\sqrt{3}}|s\rangle - \frac{\sqrt{2}}{\sqrt{3}}\left(\frac{1}{2}|p_{x}\rangle + \frac{\sqrt{3}}{2}|p_{y}\rangle\right) \end{aligned} $$

而紧束缚近似波函数 $\phi(\vec{r})$ 有

$$ \begin{aligned} \phi(\vec{r}) &= c_{A}\phi_{A}(\vec{r}) + c_{B}\phi_{B}(\vec{r})\\ & = \frac{1}{\sqrt{N}}\sum_{\vec{R}_{m}}e^{i\vec{k}\cdot\vec{R}_{m}}\left[c_{A}\varphi(\vec{r}-\vec{R}_{m}^{A}) + c_{B}\varphi(\vec{r}-\vec{R}_{m}^{B})\right] \end{aligned} $$

也可以将上面这个式子写作以下形式: $$ \phi(\vec{r}) = \frac{1}{\sqrt{N}}\sum_{\vec{R}_{m}}\left[e^{i\vec{k}\cdot\vec{R}_{m}^{A}}c_{A}\varphi(\vec{r}-\vec{R}_{m}^{A})+ e^{i\vec{k}\cdot\vec{R}_{m}^{B}}c_{B}\varphi(\vec{r}-\vec{R}_{m}^{B})\right] $$

工具介绍

紧束缚模型近似下,计算各类基础晶格的能带结构

Python下计算紧束缚模型近似