能带中的电子有效质量

电子的群速度:

$$ \vec{v}_{g} = \nabla_{\vec{k}}\omega(\vec{k})= \frac{1}{\hbar}\nabla_{\vec{k}}E(\vec{k}) $$

在一维情况下, 电子因为外力做功而获得能量 $\delta E$

$$ \delta E = F v_{g}\cdot\delta t\\ \Rightarrow \delta E = \frac{\mathrm{d}E}{\mathrm{d}k}\cdot\delta k = \hbar v_{g}\cdot\delta k $$

所以我们可以观察到一个类似于质量的参数在方程中产生作用:

$$ \hbar\frac{\mathrm{d}k}{\mathrm{d}t} = F(\hbar\frac{\mathrm{d}\vec{k}}{\mathrm{d}t}=\vec{F})\\ \frac{\mathrm{d}v_{g}}{\mathrm{d}t} = \frac{1}{\hbar}\frac{\mathrm{d}}{\mathrm{d}t}(\frac{\mathrm{d}E}{\mathrm{d}k}) = \frac{1}{\hbar}\frac{\mathrm{d}^{2}E}{\mathrm{d}k^2}\frac{\mathrm{d}k}{\mathrm{d}t} = \frac{1}{\hbar^{2}}\frac{\mathrm{d}^{2}E}{\mathrm{d}k^{2}}F = \frac{1}{m^{*}} $$

所以我们就可以定义有效质量 $m^{*}$:

$$ \frac{1}{m^{*}} = \frac{1}{\hbar^{2}}\frac{\mathrm{d}^2 E}{\mathrm{d}k^2} $$

而针对某个特定方向时, 即有

$$ \left(\frac{1}{m{*}}\right)_{\mu\nu}=\frac{1}{\hbar^{2}}\frac{\mathrm{d}^{2}E}{\mathrm{d}k_{\mu}\mathrm{d}k_{\nu}} $$

一些半定量的性质

• 能带越平, 有效质量越大;
• 有效质量是多变量函数(动量位置, 能量位置)而非常数;
• 如果色散关系是严格的抛物线($E = a(\vec{k}-\vec{k}_{0})^{2}$), 则有效质量 $m^{*}$ 为常数.

在上面的讨论中, 如果等效质量 $m^{*} = m_{0}$ 不为 $0$, 那么我们已经知道

$$ E^{2} = (\hbar k v_{g})^{2} + (m_{0}v_{g}^{2})^{2}\\ \Rightarrow E = \pm\sqrt{(\hbar k v_{g})^{2} + (m_{0}v_{g}^{2})^{2}} $$

我们引入能隙符号 $\Delta$, 且

$$ \Delta = 2m_{0}v_{g}^{2} $$

同理, 如果我们预先知道了能隙 $\Delta$, 那么我们可以得到等效质量 $m^{*}$: $$ m_{0} = \frac{\Delta}{2v_{g}^{2}} $$

可以观察到, 电子和轻空穴的有效质量约正比于能隙大小.

空穴的定义

对于全满的价带, 其电子总动量的关系为

$$ \sum\vec{k} = \vec{0} $$

所以移去一个电子(其动量为 $\vec{k}_{e}$), 价带的总动量变为

$$ \sum\vec{k} = -\vec{k}_{e} $$

我们就可以看待满价带移去电子后剩下的空位为空穴.

空穴的性质

• 空穴动量: $\vec{k}_{h} = -\vec{k}_{e}$
• 空穴能量: $E_{h}(\vec{k}_{h}) = - E_{e}(\vec{k}_{e})$
• 空穴速度: $\vec{v}_{h} = -\frac{1}{\hbar}\nabla_{\vec{k}_{h}}E_{h}(\vec{k}_{h}) = \frac{1}{\hbar}\nabla_{\vec{k}_{e}}E_{e}(\vec{k}_{e}) = \vec{v}_{e}$

和处理电子的等效质量类似, 我们也可以给出空穴的等效质量:

$$ \left(\frac{1}{m^{*}}\right)_{\mu\nu} = \frac{1}{\hbar^{2}}\frac{\mathrm{d}^{2}E}{\mathrm{d}k_{\mu}\mathrm{d}k_{\nu}}\\ m_{h}^{*} = - m_{e}^{*} $$

对于电子的受力方程一般为

$$ \hbar\frac{\mathrm{d}\vec{k}_{e}}{\mathrm{d}t} = -e(\vec{E} + \vec{v}_{e}\times\vec{B}) $$

将里面的符号进行等效替代, 就有了

$$ \hbar\frac{\mathrm{d}\vec{k}_{h}}{\mathrm{d}t} = e(\vec{E} + \vec{v}_{h}\times \vec{B}) $$

半导体中的跃迁

半导体可以直接跃迁, 也可以间接跃迁. 间接跃迁需要声子动量作为辅助. 因此直接跃迁的效率远大于间接跃迁.

重空穴带中态密度高, 光吸收时哦那个重空穴带激发电子的数目会远高于轻空穴带中的.

在直接跃迁中, 可能会出现光吸收谱的尖峰, 这个尖峰被称作 Exciton 峰(激子峰). 这是因为电子被激发后形成空穴, 而电子和空穴之间仍然存在库伦相互作用. 这种电子-空穴对被称作激子.

• Frenkel 激子: 电子空穴距离在晶格常数左右. 常见于有机物, 量级为 $\text{eV}$;
• Wannier 激子: 电子空穴距离远大于晶格常数, 常见于无机半导体. 量级为 $\text{meV}$.

我们先看 Wannier 激子. 激子的结构可以类比于氢原子, 但是电子和空穴的质量相对差会更小. 我们使用调和定义激子的有效质量:

$$ \frac{1}{\mu^{*}} = \frac{1}{m_{C}^{*}} + \frac{1}{m_{hh}^{*}}\\ (m_{C}^{*} = 0.067m_{e}, m_{hh}^{*} = 0.45m_{e}) $$

对于氢原子的能量公式我们已经很熟了:

$$ E(n) = -\frac{m_{e}e^{4}}{8\epsilon_{0}^{2}h^{2}n^{2}} = -\frac{13.6}{n^{2}}\text{eV} $$

对于激子, 要做出的替换即质量, 材料的介电常数:

$$ E(n) = -\frac{\mu^{*}}{m_{e}}\cdot\frac{1}{\epsilon_{r}^{2}}\times\frac{13.6}{n^{2}}\text{eV} $$

因为这里我们使用的是氢原子能量公式, 所以相应地, 能量的参考点也应该取为导带底的能量.

同理, 对于氢原子的玻尔半径, 有 $$ a_{0} = \frac{\epsilon_{0}h^{2}}{\pi m_{e}e^{2}} \approx 0.53\text{Å} $$

替换为激子的有效质量并且引入相对介电常数:

$$ a_{0}^{*} = \frac{\epsilon_{r}m_{e}}{\mu^{*}}\cdot 0.53 $$

能带中的粒子浓度

本征半导体

本征半导体被称为 “晶格完美的半导体”, 即 $T = 0$ 时, 电子全部都在价带, 导带中完全没有电子.

我们已经知道, 金属载流子浓度基本不随温度变化, 而半导体载流子浓度则为强烈依赖于温度.

单位能量范围内的载流子浓度为

$$ \mathrm{d}n = f(E, T)g(E)\mathrm{d}E $$

$f(E, T)$ 为 Fermi-Dirac 分布: $$ f(E,T) = \frac{1}{1+e^{(E-\color{red}{\mu})/k_{B}T}} $$ $g(E)$ 为态密度.

如果化学势离带边都很远, 即采用极限 $E - \mu\gg k_{B}T$, 那么 Fermi-Dirac 分布可以近似为 Boltzmann 分布:

$$ f(E, T) \approx e^{-(E-\mu)/k_{B}T} $$

所以在导带中找到一个电子的概率为

$$ f_{C}\approx e^{-(E-\mu)/k_{B}T} $$

相应的, 在价带中找到一个空穴的概率为

$$ f_{h} = 1 - f_{V} = 1 - \frac{1}{1 + e^{(E - \mu)/k_{B}T}} = \frac{1}{1 + e^{\mu - E}/k_{B}T}\\ \Rightarrow\lim_{\mu-E\gg k_{B}T}f_{h} = e^{-(\mu-E)/k_{B}T} $$

而对于微分式中的另一部分, 即 $g(E)$, 我们通常将其近似为抛物线色散关系.

$$ \text{导带底附近: }E - E_{C} = \frac{(k-k_{C})^{2}}{2m_{C}^{*}}\\ \text{价带顶附近: }E - E_{V} =-\frac{(k-k_{V})^{2}}{2m_{h}^{*}} $$

而对于类抛物线的能带, 我们可以移植自由电子部分的结论:

$$ g(\epsilon) = \frac{1}{\pi^{2}\hbar^{3}}(2m^{3}E)^{\frac{1}{2}}\\ \Rightarrow g_{C}(E) = a(m_{C}^{*})^{\frac{3}{2}}(E - E_{C})^{\frac{1}{2}}\\ \Rightarrow g_{V}(E) = a(m_{h}^{*})^{\frac{3}{2}}(E_{V} - E)^{\frac{1}{2}} $$

对微分式进行积分, 就能够得到导带中的电子浓度:

$$ n = \int_{E_{C}}^{\infty}\underbrace{f_{C}}_{e^{-(E-\mu)/k_{B}T}}\overbrace{g_{C}}^{a(m_{C}^{*})^\frac{3}{2}(E-E{C})^{\frac{1}{2}}}\mathrm{d}E\\ \Rightarrow n \approx a(m_{C}^{*})^{\frac{3}{2}}\int_{E_{C}}^{\infty}(E-E_{C})^{\frac{1}{2}}e^{-\frac{E-\mu}{k_{B}T}}\mathrm{d}E\\ = N_{c} e^{-\frac{E_{C}-\mu}{k_{B}T}} $$

$$ N_{C} = 2(\frac{k_{B}}{2\pi\hbar^{2}})^{\frac{3}{2}}(m_{C}^{*}T)^{\frac{3}{2}} $$

同理我们可以计算得到价带中空穴浓度:

$$ p \approx N_{V}e^{-\frac{\mu - E_{V}}{k_{B}T}} $$

$$ N_{V} = 2(\frac{k_{B}}{2\pi\hbar^{2}})^{\frac{3}{2}}(m_{h}^{*}T)^{\frac{3}{2}} $$

我们可以看到 $n$ 和 $p$ 的函数形式类似, 而且做积有

$$ np\approx WT^{3}e^{-\frac{E_{g}}{k_{B}T}} $$

上面的这个式子被称为 “Law of Mass Action”. 当然在使用这个结论前, 我们需要牢记其前提条件: $|\mu - E|\gg k_{B}T$

半导体中的化学势

我们已经求解出电子浓度和空穴浓度的表达式:

$$ n = N_{C}e^{-\frac{E_{C}-\mu}{k_{B}T}}, p = N_{V}e^{-\frac{\mu-E_{V}}{k_{B}T}} $$

对于本征半导体, $n = p$. 即有 $$ \frac{N_{V}}{N_{C}} = e^{\frac{2\mu-E_{C}-E_{V}}{k_{B}T}} $$ 而又已知 $$ N_{C}\propto (m_{C}^{*}T)^{\frac{3}{2}}, N_{V}\propto (m_{h}^{*}T)^{\frac{3}{2}} $$ 带入到上式中即有 $$ \mu = \frac{1}{2}(E_{C}+ E_{V}) + \frac{3}{4}k_{B}T\ln{\frac{m_{h}^{*}}{m_{C}^{*}}} $$ 基于以上推导, 我们可以得到一些简单推论:

• $T = 0\text{K}$ 时, $\mu = \frac{1}{2}(E_{C}+E_{V})$, 即能隙的正中间;
• $T > 0\text{K}$ 且 $m_{h}^{*} > m_{C}^{*}$ 时, $\mu$ 偏向于价带.

常识: 室温下, 本征半导体的载流子浓度约为 $10^{10\to 13}\text{cm}^{-3}$.

半导体的电导率

我们定义载流子的迁移率($\mu_{e}, \mu_{h}$):

$$ \mu = \frac{|v|}{E} $$

电荷 $q$ 的漂移速度 $v = \frac{q\tau E}{m}$, $\tau$ 为碰撞时间.

因此就有 $$ \mu_{e/h} = \frac{e\tau_{e/h}}{m_{e/h}} $$

对于半导体而言, 电导率为 $$ \sigma = ne\mu_e + pe\mu_h $$

半导体的掺杂

• 施主(Donors): n 型掺杂;
• 受主(Acceptors): p 型掺杂.

掺杂后的电子/空穴可能的状态:

• 束缚在杂质的周围, 不参与导电;
• 进入到导带或者价带, 参与导电.

取决于掺杂电子/空穴的能量/温度

• 浅掺杂能级杂质:

掺杂电子/空穴相对导带/价带边的能量较小;

此时仍然可以使用类氢原子模型. 即有

电子: $$ E_{d} = -\frac{m_{C}^{*}}{m_{e}}\cdot\frac{1}{\epsilon_{r}^{2}}\times\frac{13.6}{n^{2}}(\text{eV}) $$

空穴: $$ E_{a} = -\frac{m_{V}^{*}}{m_{e}}\cdot\frac{1}{\epsilon_{r}^{2}}\times\frac{13.6}{n^{2}}(\text{eV}) $$

室温下, 掺杂能级上的电子/空穴基本电离导带/价带, 从而参与到导电中.

• 深掺杂能级杂质:

掺杂电子/空穴相对导带/价带边的能量较大.

下图为杂质能级的位置示意图

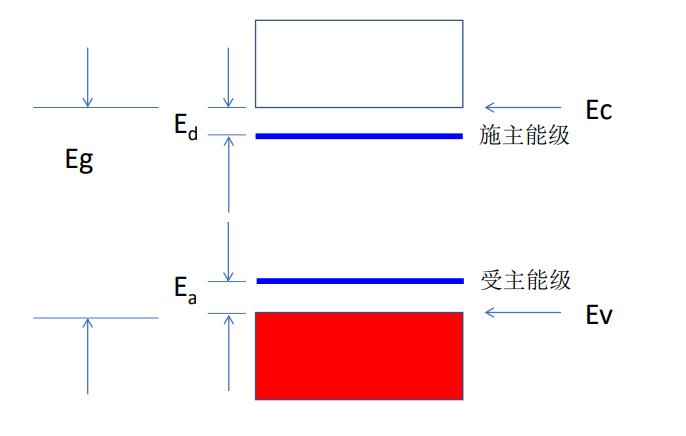
在掺杂较少的情况下, 化学势 $\mu$ 仍然在能隙范围内. 所以此时关系

$$ np = WT^{3}e^{-\frac{E_{g}}{k_{B}T}} $$

仍然成立.