基本近似

在密度泛函中我们已经提到过完整的哈密顿量形式.

$$ \hat{H}_{T} = \underbrace{\sum_{i}\frac{|\vec{p_{i}}|^2}{2m}}_{\text{价电子动能}} + \underbrace{\sum_{n}\frac{|\vec{p_{n}}|^2}{2M_{n}}}_{原子实动能} + \underbrace{\frac{1}{2}\sum_{ij}’\frac{e^2}{|\vec{r_{i}}-\vec{r_{j}}|}}_{电子间库伦势} + \underbrace{\frac{1}{2}\sum_{nn’}’\frac{Z_{n}Z_{n’}e^{2}}{|\vec{R_{n}}-\vec{R_{n’}}|}}_{原子实间库伦势} + \underbrace{\sum_{n,i}V_{n}(\vec{r_{i}}-\vec{R_{n}})}_{电子和原子实之间的相互作用} \\ +\underbrace{\hat{H}_{R}}_{相对论修正} $$

$\hat{H}_{R}$ 被称为 ‘Relativistic Corrections’, 包括了自旋-轨道的耦合项.

从第一性原理出发写出的哈密顿量当然是非常复杂的, 要进行计算就需要对其进行近似.

波恩-奥本海默绝热近似

将电子和离子实分开, 描述电子的时候认为离子实固定不动.

• 电子的哈密顿量(离子实位置不变)

$$ \hat{H}_{e} = \sum_{i}\left[\frac{\vec{p}_{i}^{2}}{2m} + \sum_{n}V_{n}(\vec{r}_{i} - \vec{R}_{n})\right] + \frac{1}{2}\sum_{ij}’\frac{e^{2}}{|\vec{r}_{i} - \vec{r}_{j}|} $$

• 离子实的哈密顿量(决定声子)

$$ \hat{H}_{c} = \sum_{n}\frac{\vec{p}_{n}^{2}}{2M_{n}}+\frac{1}{2}\sum_{nn’}’\frac{Z_{n}Z_{n’}e^{2}}{|\vec{R}_{n} - \vec{R}_{n’}|} + \underbrace{V_{\text{ec}}(\{\vec{R}_{n}\})}_{\hat{H}_{e}\text{基态对应的离子实所受的电子势场}} $$

在此过程中电子与声子之间无相互作用.

平均场近似(单电子近似)

将电子-电子之间的库伦相互作用和电子-离子实之间的库伦相互作用视为等效的平均势场, 每一个电子都在这样的平均势场中运动.

则原先的

$$ \hat{H}_{e} = \sum_{i}\left[\frac{\vec{p}_{i}^{2}}{2m} + \sum_{n}V_{n}(\vec{r}_{i} - \vec{R}_{n})\right] + \frac{1}{2}\sum_{ij}’\frac{e^{2}}{|\vec{r}_{i} - \vec{r}_{j}|} $$

写为

$$ \hat{H}_{e} = \sum_{i}\hat{H}\left(\vec{r}_{i}, \{\vec{R}_{n}\}\right)\\ \hat{H}\left(\vec{r},\{\vec{R}_{n}\}\right) = \frac{\vec{p}^{2}}{2m} + \underbrace{V(\vec{r},\{\vec{R}_{n}\})}_{\text{平均场}} $$

周期性势场近似

平均场是严格周期性势场, 具有和晶体一样的对称性.

$$ V\left(\vec{r}, \{\vec{R}_{n}\}\right) = V\left(\vec{r}\right) = V\left(\vec{r} + \vec{R}_{n}\right) $$

对于单电子而言, 其定态哈密顿量即为我们熟知的

$$ \hat{H} = -\frac{\hbar^{2}}{2m}\nabla^{2} + V(\vec{r}) $$

那么如何求得周期性势场中的单电子波函数? 首先我们要明确, 虽然哈密顿量是正格矢的周期函数, 但是该条件下的波函数并非正格矢的周期函数.

即

$$ \hat{H}\left(\vec{r} + \vec{R}\right) = \hat{H}\left(\vec{r}\right)\\ \varphi\left(\vec{r} + \vec{R}\right)\neq \varphi\left(\vec{r}\right) $$

布洛赫定理(Bloch’s Theorem)

推导

周期性势场中的电子波函数是一种调幅平面波:

$$ \varphi\left(\vec{r}\right) = e^{i\vec{k}\cdot\vec{r}}u_{k}\left(\vec{r}\right)\\ u_{k}\left(\vec{r} + \vec{R}\right) = u_{k}\left(\vec{r}\right) $$

$$ \varphi\left(\vec{r} + \vec{R}\right) = e^{i\vec{k}\cdot\vec{R}}\varphi\left(\vec{r}\right) $$

布洛赫波不会衰减, 移动变化一个正格矢只会变化其相位.

分立波矢

考虑周期性边界条件, 边界取为 $N = N_{1}\times N_{2}\times N_{3}$ 个原胞.

则

$$ \varphi\left(\vec{r} + N_{i}\vec{a}_{i}\right) = \varphi\left(\vec{r}\right) $$

又根据布洛赫定理, 即有

$$ \varphi\left(\vec{r} + N_{i}\vec{a}_{i}\right) = e^{i\vec{k}\cdot N_{i}\vec{a}_{i}}\varphi\left(\vec{r}\right) $$

所以得出

$$ e^{i\vec{k}\cdot N_{i}\vec{a}_{i}} = 1 $$

因此

$$ \vec{k} = \frac{l_{1}}{N_{1}}\vec{b}_{1} + \frac{l_{2}}{N_{2}}\vec{b}_{2} + \frac{l_{3}}{N_{3}}\vec{b}_{3} $$

$k$ 点的密度为 $n_{k} = \left(\frac{L}{2\pi}\right)^{3} = \frac{V}{8\pi^{3}}$.

倒格子原胞的体积为

$$ \vec{b}_{1}\cdot\left(\vec{b}_{2}\times\vec{b}_{3}\right) = \frac{(2\pi)^{3}}{\Omega} = \frac{(2\pi)^{3}}{V/N} $$

所以倒格子原胞中的 $k$ 点数目为

$$ N_{k} = n_{k}\cdot \Omega^{*} = N $$

波矢特性

晶体的平移对称性:

$$ e^{i\vec{G}\cdot\vec{R}} = 1 $$

即有

$$ e^{i\left(\vec{k}+\vec{G}\right)}\varphi\left(\vec{r}\right) = e^{i\vec{k}\cdot\vec{R}}e^{i\vec{G}\cdot\vec{R}}\varphi\left(\vec{r}\right) = e^{i\vec{k}\cdot\vec{R}}\varphi\left(\vec{r}\right) $$

所以 $\vec{k}$ 和 $\vec{k}’ = \vec{k} + \vec{G}$ 实际上是等价的.

因此布洛赫波的波矢只需要考虑第一布里渊区内的波矢即可, 第一布里渊区以外的 $k$ 点都可以通过若干个 $\vec{G}$ 平移到第一布里渊区.

能谱特征

单电子波函数

$$ \left[-\frac{\hbar^{2}}{2m}\nabla^{2} + V\left(\vec{r}\right)\right]\varphi\left(\vec{r}\right) = E\varphi\left(\vec{r}\right) $$

代入布洛赫波形式的波函数 $\varphi\left(\vec{r}\right) = e^{i\vec{k}\cdot\vec{r}}u_{k}\left(\vec{r}\right)$, 即有

$$ \left[-\frac{\hbar^{2}}{2m}\nabla^{2} + V\left(\vec{r}\right)\right]e^{i\vec{k}\cdot\vec{r}}u_{k}\left(\vec{r}\right) = E\left(\vec{k}\right)e^{i\vec{k}\cdot\vec{r}}u_{k}\left(\vec{r}\right)\\ \Downarrow{\text{两边左乘}e^{-i\vec{k}\cdot\vec{r}}}\\ e^{-i\vec{k}\cdot\vec{r}}\left[-\frac{\hbar^{2}}{2m}\nabla^{2} + V\left(\vec{r}\right)\right]e^{i\vec{k}\cdot\vec{r}}u_{k}\left(\vec{r}\right) = e^{-i\vec{k}\cdot\vec{r}}E\left(\vec{k}\right)e^{i\vec{k}\cdot\vec{r}}u_{k}\left(\vec{r}\right)\\ \Downarrow\\ \left[\frac{\hbar^{2}}{2m}\left(-i\nabla+\vec{k}\right)^{2} + V\left(\vec{r}\right)\right]u_{k}(\vec{r}) = E_{k}u_{k}\left(\vec{r}\right)\\ \Downarrow\\ \hat{H}_{k}u_{k}\left(\vec{r}\right) = E\left(\vec{k}\right)u_{k}\left(\vec{k}\right) $$

$u_{k}\left(\vec{r}\right)$ 需要满足周期性边界条件 $$ u_{k}\left(\vec{r} + \vec{R}\right) = u_{k}\left(\vec{r}\right) $$ 所以要求解能量本征值, 其实只需要在晶格的一个原胞内进行就可以达到目的.

我们可以得出以下初步结论:

1. 能量本征值是分立的, 并且使用指标 $n$ 来区分它们($E_{n}$);
2. 每个波矢 $\vec{k}$ 都对应着无数多个能量 $E_{n}(n\in\mathbb{Z})$;
3. 平移对称性 $$ \varphi_{n,\vec{k}+\vec{G}}\left(\vec{r}\right) = \varphi_{n,\vec{k}}\left(\vec{r}\right)\\ E_{n}\left(\vec{k} + \vec{G}\right) = E_{n}\left(\vec{k}\right) $$ 即对确定的能级指标 $n$, 能量色散曲线 $E\left(\vec{k}\right)$ 有上下界, 且形成一条能带.

弱周期性近似(近自由电子近似)

使用的是微扰论的思想来求解.

• 周期性势场非常微弱;
• 哈密顿量为自由电子 + 微弱的周期性势场

这种模型通常适用于 $s$ 或者 $p$ 的金属.

考虑一维自由电子, 其能量为

$$ E = \frac{\hbar^{2}\color{red}{k^{2}}}{2m} $$

现在加入一维晶格的周期性势场, 其示意图如下:

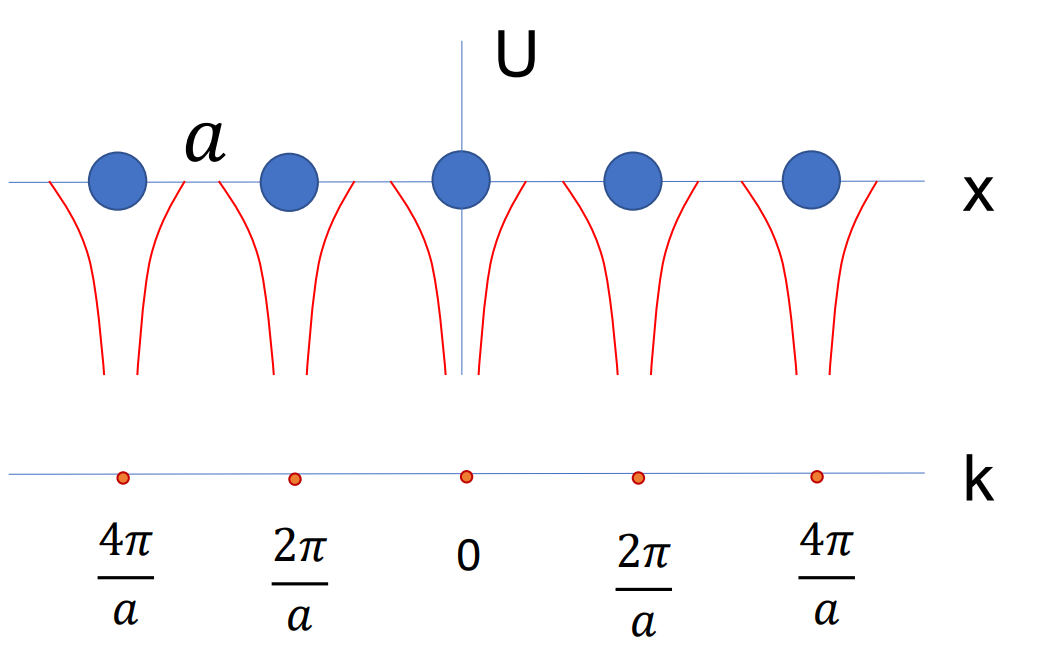
所以现在单电子的哈密顿量为

$$ \hat{H} = \hat{H}_{0} + \hat{H}’\\ \left(\hat{H}_{0} = -\frac{\hbar^{2}}{2m}\nabla^{2}\right) $$

因为周期性势场的平均值为常数, 为了便于计算不妨将其取值为 $0$.

对于 $\hat{H}_{0}$, 可以求得其本征波函数为

$$ \varphi_{k}^{0}(x) = \frac{1}{\sqrt{L}}e^{ikx} $$

对应的本征能量则为

$$ E_{k}^{0} = \frac{\hbar^{2}\vec{k}}{2m} $$

非简并微扰处理

根据微扰论相关结论, 我们可以知道一级修正

$$ \varphi_{k}(x) = \varphi_{k}^{0}(x) + \sum_{k’(k’\neq k)}\frac{\langle k’|\hat{H}’|k\rangle}{E_{k}^{0} - E_{k’}^{0}}\varphi_{k’}^{0}(x) $$

$|k\rangle$ 为自由电子的本征态.

具体到我们讨论的情景, 即为

$$ \boxed{\varphi_{k}(x) = \varphi_{k}^{0}(x) + \sum_{k’(k’\neq k)}\frac{\langle k’|V(x)|k\rangle}{E_{k}^{0} - E_{k’}^{0}}\varphi_{k’}(x)} $$

考虑矩阵元 $\langle k’|V(x)|k\rangle$, 有

$$ \langle k’|V(x)|k\rangle = \frac{1}{L}\int e^{-i(k’-k)x}V(x)\mathrm{d}x $$

因为晶格具有平移周期性, 即有 $k’ - k = G$

$$ \langle k’|V(x)|k\rangle = \frac{1}{L}\int e^{-iGx}V(x)\mathrm{d}x $$

势场的傅里叶级数展开 $$ V(x) = \sum_{G}V_{G}e^{iG\cdot x}\\ V_{G} = \frac{1}{L}\int e^{-iGx}V(x)\mathrm{d}x $$

所以有

$$ \langle k’|V(x)|k \rangle = V_{G}(G = k’-k) $$

所以原一级修正表达式可以写为

$$ \varphi_{k} = \varphi_{k}^{0}(x) + \sum_{k’(k’\neq k)}\frac{\langle k’|V(x)|k\rangle}{E_{k}^{0}-E_{k’}^{0}}\varphi_{k’}^{0}(x)\\ = \varphi_{k}^{0}(x) + \sum_{k’(k’\neq k)}\frac{V_{G}}{E_{k}^{0} - E_{k’}^{0}}\varphi_{k’}^{0}(x) $$

将平面波函数代入, 得到

$$ \varphi_{k}(x) = \frac{1}{\sqrt{L}}e^{ikx} + \sum_{G}\frac{V_{G}}{\frac{\hbar^{2}}{2m}\left[k^{2} - \left(k + G\right)^{2}\right]}\frac{1}{\sqrt{L}}e^{i\left(k + G\right)x}\\ = \frac{1}{\sqrt{L}}\underbrace{\left\{1 + \sum_{G}\frac{V_{G}}{\frac{\hbar^{2}}{2m}\left[k^{2} - \left(k + G\right)^{2}\right]}e^{iG\cdot x}\right\}}_{u_{k}(x)} $$

可以发现, 使用了一级修正之后的波函数仍然是一个布洛赫波的函数

所以能量的一级修正

$$ \langle k|V(x)|k\rangle = \frac{1}{L}\int_{0}^{L}V(x)\mathrm{d}x = \langle V\rangle = 0 $$

这是因为我们已经假定了周期性势场的平均值为 $0$.

所以一级修正对于我们的研究而言没有什么意义, 需要进一步考虑能量的二级修正.

$$ E_{k} = E_{k}^{0} + E_{k}^{1} + \color{red}{E_{k}^{2}} + \dots $$

$$ \boxed{\color{red}{E_{k}^{2}} = \sum_{k’}\frac{|\langle k’|V(x)|k\rangle|^{2}}{E_{k}^{0} - E_{k’}^{0}} = \sum_{G}\frac{|V_{G}|^{2}}{\frac{\hbar^{2}}{2m}\left[k^{2}-\left(k + G\right)^{2}\right]}} $$

我们可以分出两种情况对该式进行分析:

1. 远离布里渊区边界, 即 $(k + G)^{2} \gg k^{2}$;

则修正项可以忽略, 可以将该情形考虑为自由电子

2. 在布里渊区边界, 即 $(k + G)^{2} = k^{2}$.

这个时候分母为 $0$, 即出现发散情况. 我们采用的非简并微扰方法无法处理这种情况. 所以需要考虑简并微扰论的方法来处理在布里渊区边界上的问题.

简并微扰处理

在一维情况下, 可以将布里渊区边界附近的能量近似为二重简并 $\varphi_{k}^{0}$ 和 $\varphi_{k’}^{0}(x)$.

所以构建其线性组合为新的波函数为

$$ \varphi(x) = a\varphi_{k}^{0}(x) + b\varphi_{k’}^{0}(x) $$

将这个波函数带入到单电子的薛定谔方程中:

$$ \left[-\frac{\hbar^{2}}{2m}\frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}} + V(x) - E\right]\varphi(x) = 0\\ \Rightarrow a\left[E_{k}^{0} - E + V(x)\right]\varphi_{k}^{0} + b\left[E_{k’}^{0} - E + V(x)\right]\varphi_{k’}^{0} = 0 $$

分别左乘 $\varphi_{k}^{0*}$ 和 $\varphi_{k’}^{0*}$ 并且积分, 得到方程组

$$ \int\varphi_{k}^{0*}\left\{a\left[E_{k}^{0} - E + V(x)\right]\varphi_{k}^{0} + b\left[E_{k’}^{0} - E + V(x)\right]\varphi_{k’}^{0}\right\}\mathrm{d}x = 0\\ \int\varphi_{k’}^{0*}\left\{a\left[E_{k}^{0} - E + V(x)\right]\varphi_{k}^{0} + b\left[E_{k’}^{0} - E + V(x)\right]\varphi_{k’}^{0}\right\}\mathrm{d}x = 0 $$

因为 $\langle V\rangle = 0$, 所以可以进一步化简得到

$$ \left(E_{k}^{0} - E\right)\color{red}{a} + V_{G}^{*}\color{red}{b} = 0\\ V_{G}\color{red}{a} + (E_{k’}^{0} - E)\color{red}{b} = 0 $$

利用线性代数相关知识可知, 方程组若有解, 则应满足系数行列式为 $0$:

$$ \begin{vmatrix} E_{k}^{0} - E & V_{G}^{*}\\ V_{G} & E_{k’}^{0} - E \end{vmatrix} = 0 \Rightarrow\\ (E_{k}^{0} - E)(E_{k’}^{0} - E) - |V_{G}|^{2} = 0\\ \Rightarrow\\ E_{k\pm} = \frac{1}{2}\left\{\left(E_{k}^{0} + E_{k’}^{0}\right)\pm\sqrt{(E_{k}^{0} + E_{k’}^{0})^{2} + 4|V_{G}|^{2}}\right\} $$

同样地, 我们分出两种情况对该表达式进行分析:

1. 布里渊区边界处($E_{k}^{0} = E_{k’}^{0}$)

$$ E_{k\pm} = E_{k}^{0}\pm|V_{G}| $$

即在布里渊区的边界有能隙被打开.

2. 远离布里渊区($|E_{k}^{0} - E_{k’}^{0}|\gg|V_{G}|$)

$$ E_{k\pm}= \begin{cases} E_{k’}^{0} + \frac{|V_{G}|^{2}}{E_{k’}^{0} - E_{k}^{0}}\\ E_{k}^{0} + \frac{|V_{G}|^{2}}{E_{k’}^{0} - E_{k}^{0}}\\ \end{cases} $$

即能量高的态, 能量会变得更高; 能量低的态, 能量会变得更低.

3. 靠近布里渊区边界($|E_{k}^{0} - E_{k’}^{0}|\ll|V_{G}|$)

则修正后能量特化为

$$ E_{k\pm} = \frac{1}{2}\left\{E_{k}^{0} + E_{k’}^{0} \pm\left[2|V_{G}| + \frac{(E_{k’}^{0} - E_{k}^{0})^{2}}{4|V_{G}|}\right]\right\} $$

如果非常靠近布里渊区边界, 即 $k + \frac{G}{2}\approx 0$, 则

$$ E_{k}^{0} + E_{k’}^{0} = \frac{\hbar^{2}}{2m}\left[k^{2} + (k + G)^{2}\right] = \frac{\hbar^{2}}{2m}\left[\left(k + \frac{G}{2} - \frac{G}{2}\right)^{2} + \left(k + \frac{G}{2} + \frac{G}{2}\right)^{2}\right]\\ = 2E_{0} + \frac{\hbar^{2}}{m}\left(k + \frac{G}{2}\right)^{2} $$

将该结果代回到能量修正项中:

$$ E_{k\pm} = (E_{0} \pm |V_{G}|) + \frac{\hbar^{2}}{2m}\left(k + \frac{G}{2}\right)^{2} \pm \frac{(E_{k’}^{0} - E_{k}^{0})^{2}}{8|V_{G}|} $$

详细计算 $(E_{k’}^{0} - E_{k}^{0})^{2}$:

$$ (E_{k’}^{0} - E_{k}^{0})^{2} = \left(\frac{\hbar^{2}}{2m}\right)^{2}[k’^{2} - k^{2}]^{2} = \left(\frac{\hbar^{2}}{2m}\right)^{2}[(k’ + k)(k’ - k)]^{2}\\ = \left(\frac{\hbar^{2}}{2m}\right)^{2}G^{2}(2k + G)^{2} = 4\left(\frac{\hbar^{2}}{2m}\right)^{2}G^{2}\left(k + \frac{G}{2}\right)^{2} $$

于是得到该情况下的能带

$$ E_{k\pm} \approx (E_{0}\pm |V_{G}|) + \frac{\hbar^{2}}{2m}\left(k + \frac{G}{2}\right)^{2} \pm \left(\frac{\hbar^{2}}{2m}\right)^{2} \frac{G^{2}}{2|V_{G}|}\left(k + \frac{G}{2}\right)^{2} $$

即该情况下的色散曲线为抛物线.

Kronig-Penney Model

推导

设有周期性方势阱

$$ V(x) = \begin{cases} 0 & x\in[0,a]\\ U_{0} & x\in[a,a+b] \end{cases}\\ (V(x+a+b)=V(x)) $$

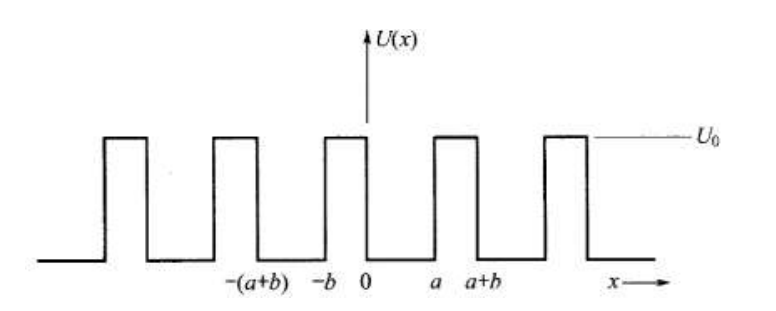
我们按照形式解的方式写出波函数:

$$ \begin{cases} \psi(x) = Ae^{iKx} + Be^{-iKx} & \epsilon = \frac{\hbar^{2}K^{2}}{2m} & (x\in[0,a])\\ \psi(x) = Ce^{Qx} + De^{-Qx} & U_{0} -\epsilon = \frac{\hbar^{2}Q^{2}}{2m} & (x\in[-b,0]) \end{cases} $$

• 因为是周期势, 所以波函数解一定是布洛赫形式.

• 连续性方程(波函数连续 & 一阶导数连续)

$$ \begin{aligned} \begin{cases} A + B &= C + D\\ iK(A-B) &= Q(C - D)\\ Ae^{iKa} + Be^{-iKa} &= (Ce^{-Qb} + De^{Qb})e^{ik(a+b)}\\ iK(A^{iKa} - Be^{-iKa}) &= Q(Ce^{-Qb} - De^{Qb})e^{ik(a+b)} \end{cases} \end{aligned} $$

这实际上是一个四元一次方程组, 如果方程有解, 则系数矩阵的行列式一定为 $0$.

$$ \frac{Q^{2}-K^{2}}{2QK}\sinh{Qb}\sin{Ka} + \cosh{Qb}\cos{Ka} = \cos{k(a+b)} $$

$\delta$ 势近似

取周期性 $\delta$ 势对上述结论进行近似, 即条件

$$ b\rightarrow 0;U_{0}\rightarrow \infty; \frac{Q^{2}ba}{2} = P $$

即可得到

$$ \frac{Q^[2]-K^{2}}{2QK}\sinh{Qb} = \frac{P}{Ka};\cosh{Qb} = 1\\ \Downarrow\\ \boxed{\frac{P}{Ka}\sin{Ka} + \cos{Ka} = \cos{ka}} $$

$$ \epsilon = \frac{\hbar^{2}K^{2}}{2m}, (-1\leq \cos{ka} \leq 1) $$

周期势中的电子波动方程

对具有周期性的物理量进行傅里叶变换是常见的处理方法. 对一周期性势场进行傅里叶级数展开:

$$ U(x) = \sum_{G}U_{G}e^{iGx} $$

同理, 对电子波函数进行傅里叶级数展开

$$ \psi(x) = \sum_{k}C(k)e^{ikx} $$

前面我们已经讨论过如何将 $k$ 约定在第一布里渊区进行讨论. 我们可以借助倒格矢 $G$ 来做到这一点:

$$ \psi_{k}(x) = \sum_{G}C(k - G)e^{i(k - G)x} $$

于是波动方程

$$ \left(\frac{p^{2}}{2m} + U(x)\right)\psi(x) = \epsilon\psi(x)\\ \Downarrow{\mathcal{F}[U(x)],\mathcal{F}[\psi(x)]}\\ \sum_{k}\frac{\hbar^{2}}{2m}k^{2}C(k)e^{ikx} + \sum_{G}\sum_{k}U_{G}C(k)e^{i(k + G)x} = \epsilon\sum_{k}C(k)e^{ikx}\\ \Downarrow\\ \sum_{k}\left[\frac{\hbar^{2}k^{2}}{2m}C(k)e^{ikx}-\epsilon C(k)e^{ikx} + \sum_{G}U_{G}C(k -G)e^{ikx}\right] = 0\\ \Downarrow\\ \left(\frac{\hbar^{2}k^{2}}{2m}-\epsilon\right)C(k) + \sum_{G}C(k-G)=0 $$

这就是关于傅里叶系数 $C(k)$ 的线性方程组, 即中心方程.

如果该方程组有解, 则其系数矩阵的行列式必定为 $0$. 原则上行列式应该为无限长宽, 但是实际上取一定截断也可以获得足够近似的能量 $\epsilon$.

设 $g$ 为最小的倒格矢 $G$, 且势能中的傅里叶分量 $U_{g} = U$. 则中心方程系数行列式为

$$ \left|\begin{array}{c|ccccc|c} \ddots & \vdots & \vdots &\vdots &\vdots &\vdots & \ddots\\ \hline \dots & \lambda_{k-2g}-\epsilon & U & 0 & 0 & 0 & \dots\\ \dots & U & \lambda_{k-g} -\epsilon & U & 0 & 0 & \dots\\ \dots & 0 & U & \lambda_{k}-\epsilon & U & 0 & \dots\\ \dots & 0 & 0 & U & \lambda_{k+g} -\epsilon & U & \dots\\ \dots & 0 & 0 & 0 & U & \lambda_{k+2g} & \dots\\ \hline \ddots & \vdots & \vdots &\vdots &\vdots &\vdots & \ddots\\ \end{array}\right| = 0 $$

这里就是取的 $5\times 5$ 截断的示意图.

空格点近似

推导

前面我们已经谈到过, 能带结构可以表示在第一布里渊区中. 如果能带能量可以近似为自由电子的能量 $$ \epsilon_{\mathbf{k}} = \frac{\hbar^{2}\mathbf{k}^{2}}{2m} $$

那么我们也应该将自由电子的能量表示在第一布里渊区.

实际上电子的波矢当然不一定在第一布里渊区内, 但是我们知道每个 $\mathbf{k}$ 点一定存在第一布里渊区中的 $\mathbf{k}’$ 点与之对应. 也就是说, 我们需要确定一个倒格子矢量 $\mathbf{G}$, 使得

$$ \mathbf{k}’ + \mathbf{G} = \mathbf{k} $$

那么映射后的自由电子能量即为

$$ \epsilon(k_{x},k_{y},k_{z}) = \frac{\hbar^{2}(\mathbf{k}+ \mathbf{G})^{2}}{2m} = \frac{\hbar^{2}}{2m}\left[(k_{x} + G_{x})^{2} + (k_{y} + G_{y})^{2} + (k_{z} + G_{z})^{2}\right] $$

例子

假定为低能自由电子能带, 求简单立方晶格中 $[100]$ 方向的能量色散函数.

两种晶面表示指标

假设晶面在各轴的截距为 $a_{1},a_{2},a_{3}$. 则

• $\left(a_{1}^{-1}, a_{2}^{-1}, a_{3}^{-1}\right)$;
• $[a_{1},a_{2},a_{3}]$. 上划线表示负号, 如 $[u\overline{v}w]$.

接下来我们需要按照能级简并来对各类 $G$ 进行分类. 简单立方晶格的倒格子基矢的长度为 $\frac{2\pi}{a}$, 所以倒格矢 $G$ 的分量也必然是 $\frac{2\pi}{a}$ 的整倍数. 所以我们用另一种方法来区分 $G$, 即将其写为 $G\cdot\frac{a}{2\pi}$. 比如

$$ \vec{G} = \frac{2\pi}{a}(0,0,0)\Rightarrow \frac{Ga}{2\pi}:[000] $$

因为我们已经假定是求 $[100]$ 方向的色散, 所以 $\vec{k} = k_{x} \hat{x}$, 因此原本的自由电子能量特化为公式

$$ \epsilon(\vec{k}) = \frac{\hbar^{2}}{2m}\left[(k_{x} + G_{x})^{2} + G_{y}^{2} + G_{z}^{2}\right] $$

而不同的 $\frac{Ga}{2\pi}$ 相当于把对应的倒格矢分量填入各 $G_{i}$ 中. 比如

$$ \frac{Ga}{2\pi}:[xyz]\Rightarrow\epsilon(\vec{k})=\epsilon(k_{x}00)= (k_{x}+x\cdot\frac{2\pi}{a})^{2} + (y\cdot\frac{2\pi}{a})^{2} + (z\cdot\frac{2\pi}{a})^{2} $$

列出所有可能的 $\frac{Ga}{2\pi}:[xyz]$, 求解能量并且按照简并将其聚类, 就可以得到色散关系.

这里我们不需要将所有的 $\frac{Ga}{2\pi}$ 都列出来, 因为 $k$ 是无穷大的, 也没有必要也不可能完全写出. 我们可以写几个简单的, 靠近第一布里渊区的.

$$ \begin{array}{|c|c|c|c|} \hline \text{能带} & \frac{Ga}{2\pi} & \epsilon(000) & \epsilon(k_{x}00)\\ \hline 1 & 000 & 0 & k_{x}^{2} \\ \hline 2,3 & 100,\overline{1}00& \left(\frac{2\pi}{a}\right)^{2} & \left(k_{x}\pm\frac{2\pi}{a}\right)^{2}\\ \hline 4,5,6,7 & 010,0\overline{1}0,001,00\overline{1} & \left(\frac{2\pi}{a}\right)^{2} & k_{x}^{2} + \left(\frac{2\pi}{a}\right)^{2}\\ \hline 8,9,10,11 & 110,101,1\overline{1}0,10\overline{1} & 2\left(\frac{2\pi}{a}\right)^{2} & \left(k_{x} + \frac{2\pi}{a}\right)^{2} + \left(\frac{2\pi}{a}\right)^{2}\\ \hline 12,13,14,15 & \overline{1}10,\overline{1}01,\overline{11}0,\overline{1}0\overline{1} & 2\left(\frac{2\pi}{a}\right)^{2} & \left(k_{x} - \frac{2\pi}{a}\right)^{2} + \left(\frac{2\pi}{a}\right)^{2}\\ \hline 16,17,18,19 & 011,0\overline{1}1,01\overline{1},0\overline{1}\overline{1} & 2\left(\frac{2\pi}{a}\right)^{2} & k_{x}^{2} + 2\left(\frac{2\pi}{a}\right)^{2}\\ \hline \end{array} $$

对应的能带图即为

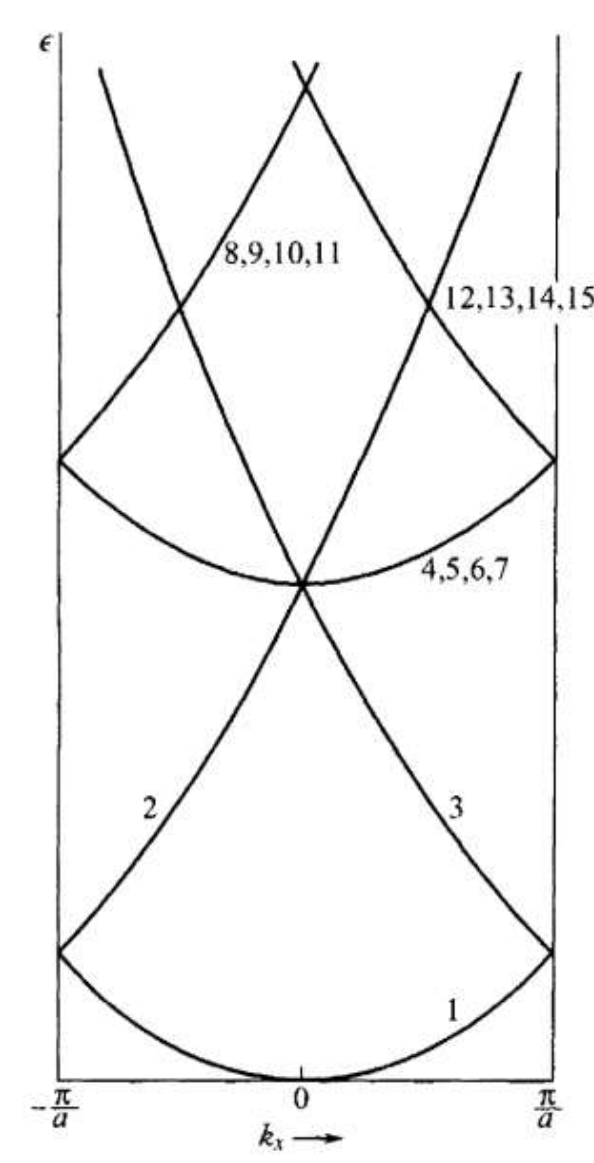
1. 在布里渊区的边界处, 即 $\frac{G}{2}$, 假设 $U_{G}$ 与自由电子的动能相比较小, 而

$$ k^{2} = \left(\frac{G}{2}\right)^{2}, (k - G)^{2} = \left(\frac{G}{2}\right)^{2}. $$

前面我们已经知道中心方程的具体形式, 所以我们这里仅保留 $C(\frac{G}{2}), C(-\frac{G}{2})$ 两个系数, 即有

$$ \left|\begin{array} \lambda-\epsilon & U \\ U & \lambda - \epsilon \\ \end{array}\right|=0\\ \Downarrow\\ \epsilon_{\pm} = \lambda \pm U = \frac{\hbar^{2}}{2m}\left(\frac{G}{2}\right)^{2}\pm U $$

观察到两个系数比值为 $$ \frac{C\left(-\frac{G}{2}\right)}{C\left(\frac{G}{2}\right)} = \frac{\epsilon-\lambda}{U} = \pm 1 $$

这和我们前面使用简并微扰处理得出的结论相同.

2. 在波矢 $k$ 点在布里渊区边界 $\frac{G}{2}$ 附近时, 即有

$$ \left|\begin{array} \lambda_{k}-\epsilon & U\\ U & \lambda_{k-G}-\epsilon \\ \end{array}\right| = 0\\ \Downarrow(\widetilde{K}=k-\frac{G}{2})\\ \epsilon_{\widetilde{K}}(\pm) \approx \frac{\hbar^{2}}{2m}\left[\left(\frac{G}{2}\right)^{2} + \widetilde{K}^{2}\right]\pm\left[U+\frac{2\lambda}{U}\frac{\hbar^{2}\widetilde{K}^{2}}{2m}\right] = \epsilon_{\pm} + \frac{\hbar^{2}\widetilde{K}^{2}}{2m}\left(1\pm\frac{2\lambda}{U}\right). $$

几何结构因子和能隙的关系

我们使用以下几个参数:

• $\vec{d}_{i}$, 第 $i$ 个原子在原胞中的位置, 可以理解为相对位置矢量;

• $V(\vec{r})$, 是空间上 $\vec{r}$ 位置的总势场;

• $v_{i}(\vec{r}-\vec{d}_{i})$ 是原胞中第 $i$ 个原子产生的势场.

我们可以推断: 总势场应当是原胞中所有原子的势场之和, 即写作

$$ V(\vec{r}) = \sum_{i}v_{i}(\vec{r} - \vec{d}_{i}) $$

将 $v_{i}(\vec{r} - \vec{d}_{i})$ 进行傅里叶展开:

$$ v_{i}(\vec{r}-\vec{d}_{i}) = \sum_{\vec{G}_{n}}v_{i}(\vec{G}_{n})e^{i\vec{G}_{n}\cdot\left(\vec{r}-\vec{d}_{i}\right)}\\ \Downarrow\\ V(\vec{r} = \sum_{i})\sum_{\vec{G}_{n}}v_{i}(\vec{G}_{n})e^{i\vec{G}_{n}\cdot\left(\vec{r}-\vec{d}_{i}\right)} = \sum_{\vec{G}_{n}}\color{red}{\sum_{i}v_{i}(\vec{G}_{n})e^{-i\vec{G}_{n}\cdot\vec{d}_{i}}}e^{i\vec{G}_{n}\cdot\vec{r}}\\ \Downarrow\\ V(\vec{r}) = \sum_{\vec{G}_{n}}\color{red}{V(\vec{G}_{n})}e^{i\vec{G}_{n}\cdot\vec{r}}\left(\color{red}{V(\vec{G}_{n}) = \sum_{i}v_{i}(\vec{G}_{n})e^{i\vec{G}_{n}\cdot\vec{d}_{i}}}\right) $$

这里的 $V(\vec{G}_{n})$ 即被称为能隙的几何形状因子.

类比 X 光散射中的几何结构因子 $$ S(\vec{G}) = \sum_{i}f_{i}(\vec{G})e^{-i\vec{G}\cdot\vec{d}_{i}} $$

如果复式原胞中的基元是同种原子, 那么几何结构因子将会特化为

$$ V(\vec{G}_{n}) = v(\vec{G}_{n})\sum_{i}e^{-i\vec{G}_{n}\cdot\vec{d}_{i}} $$

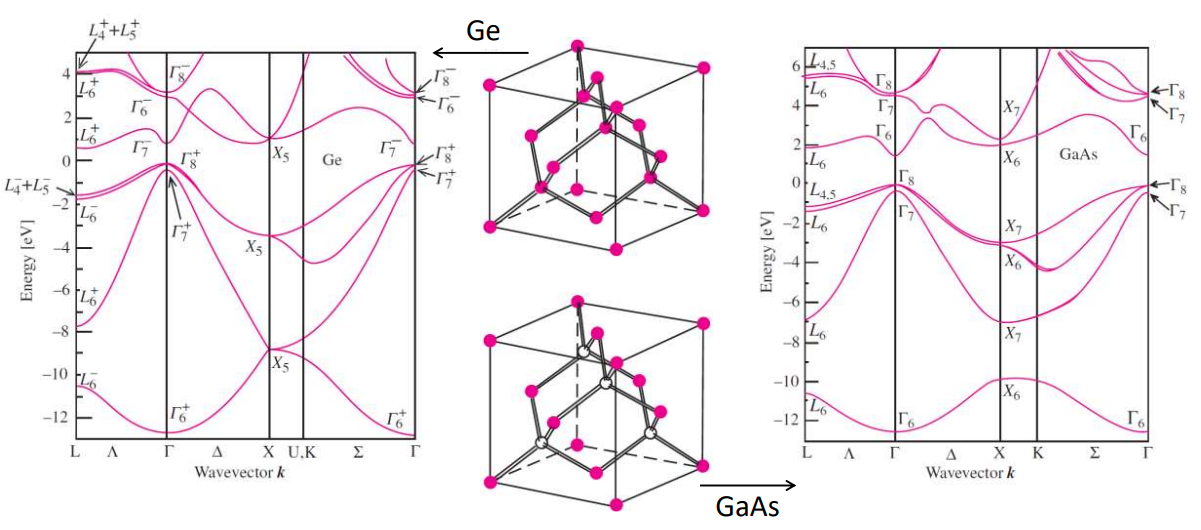
Ga(31), Ge(32), As(33) 是相邻元素, 纯 Ge 和 GaAs 的晶体结构都是类金刚石结构, 但是前者可以在特定布里渊区边界出现无能隙现象.