一般的洛伦兹力方程: $$ \hbar\frac{\mathrm{d}\vec{k}}{\mathrm{d}t} = - e\vec{v}\times\vec{B} $$
$\frac{\mathrm{d}\vec{k}}{\mathrm{d}t}$ 显然会始终垂直于 $\vec{v}$ 和 $\vec{B}$.
因此沿着 $\vec{B}$ 方向的波矢将会保持不变.
能带电子的群速度:
$$ \vec{v} = \frac{1}{\hbar}\nabla_{k}E(\vec{k}) $$
所以根据上面的推测, $\frac{\mathrm{d}\vec{k}}{\mathrm{d}t}$ 将会垂直于 $\nabla_{k}E(\vec{k})$
在均匀外磁场下, 实空间和动量空间中电子都做回旋运动.
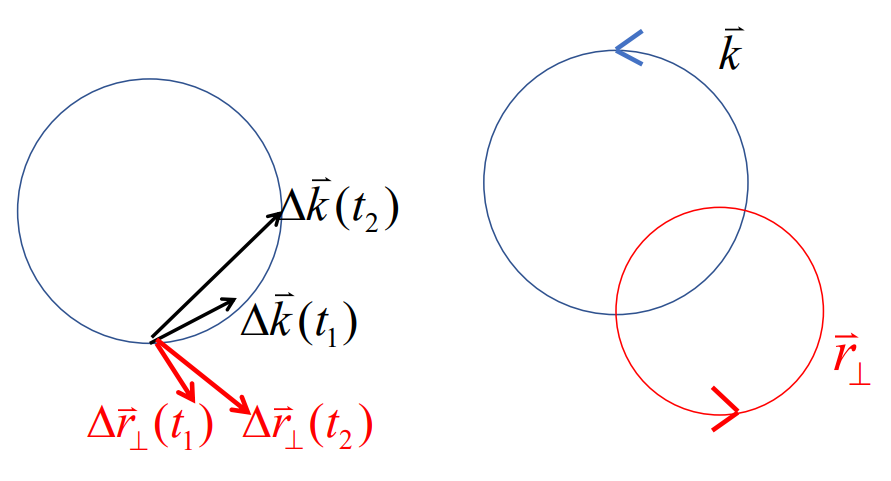
k 空间中的电子回旋频率
不妨以自由电子近似下的球形等能面为例, 且取 $k_{z} = 0$.
即有回旋运动周期
$$ T = \frac{\oint\mathrm{d}k}{|\mathrm{d}\vec{k}/\mathrm{d}t|}\\ = \frac{2\pi K}{\frac{1}{\hbar}evB}=\frac{2\pi}{eB}\color{red}{\frac{\hbar K}{v}} = \frac{2\pi\color{red}{m}}{eB} $$
所以对应的回旋频率:
$$ \omega_{c} = \frac{2\pi}{T} = \frac{eB}{m_{c}^{*}} $$
这是一个普适结论, 即使是非自由电子近似, 对应的 $m_{c}^{*}$ 是有效回旋质量
$m_{c}^{*}$ 不一定等于能带有效质量 $m^{*}$
磁场中运动的能量量子化
朗道能级
- 考虑抛物线型色散关系
- 不考虑自旋和磁场的相互作用(塞曼分裂)
我们就可以获得朗道能级:
$$ E(k) = \frac{\hbar^{2}}{2m}k_{z}^{2} + \left(n + \frac{1}{2}\right)\hbar\omega_{c} $$
- 平行 $\vec{B}$: 能量准连续;
- 垂直 $\vec{B}$: 分离能级.
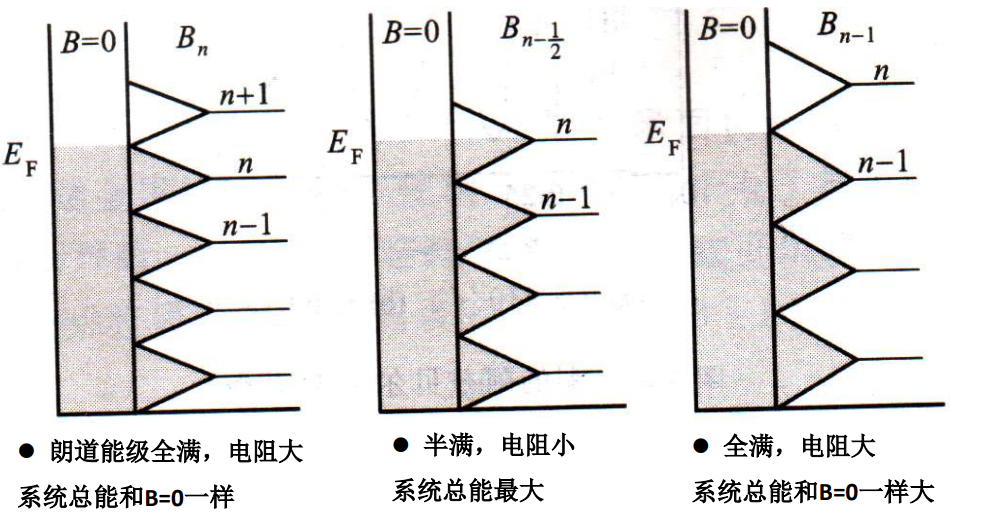
朗道能级简并度
每个朗道能级上能够允许多少个电子存在?
- 无磁场时
$x-y$ 平面内: $$ E(\vec{k}) = \frac{\hbar^{2}}{2m}(k_{x}^{2} + k_{y}^{2}) $$
- 有磁场时
$x-y$ 平面内的所有能态全部简并到朗道能级.
相邻的两个朗道环 $L_{n}, L_{n+1}$ 所围面积内的全部电子态简并到了同一能级.
而这一壳层中的态数目为
$$ n_{k} = \Delta A \times \frac{S}{4\pi^{2}}\\ = \pi\left[\Delta(k_{x}^{2} + k_{y}^{2})\right]\times \frac{S}{4\pi^{2}}\\ = \frac{2\pi m\Delta E}{\hbar^{2}}\times \frac{S}{4\pi^{2}}\\ = \frac{2\pi m\hbar\omega_{c}}{\hbar^{2}}\times \frac{S}{4\pi^{2}}\\ = \frac{4\pi^{2}eB}{h}\times \frac{S}{4\pi^{2}} = \frac{eBS}{\hbar} $$
所以朗道能级的简并度 $p$ 为
$$ p = 2n_{k} = \frac{2e}{h}BS = \frac{BS}{\Phi_{0}} $$
$\Phi_{0} = \frac{h}{2e} \approx 2.067\times 10^{-15} (\text{Wb})$ 为磁通量子
因为磁通量子数量级很小, 所以稍微大一些的 $B$ 都会造成极高度的简并.
能带电子的轨道量子化
假定 $$ B = 1(\text{T}), \hbar\omega_{c} = 10^{-4}(\text{eV}) $$ 则朗道能级数的量级约为 $n$ ~ $10^{4}$
所以属于高量子态条件.
对于高量子态条件, 可以利用经典量子论来处理.
闭合回旋轨道的波尔-索末菲量子化条件 $$ \oint\vec{p}\cdot\mathrm{d}\vec{r} = (n + \gamma)\cdot 2\pi\hbar $$
$\vec{p} = \hbar\vec{k} - e\vec{A}$, $n$ 为整数, $\gamma = 1/2$ 为常数.
所以可以得到
$$ A_{r} = \frac{2\pi\hbar}{eB}(n + \gamma) $$
$A_{r}$ 为电子在实空间中轨道垂直磁场的面积. 上式推导用到了环量定理.
而我们已经推导出实空间和倒空间运动之间的关系
$$ \hat{B} \times \frac{\mathrm{d}\vec{k}}{\mathrm{d}t} = -\frac{eB}{\hbar}\frac{\mathrm{d}\vec{r}_{\perp}}{\mathrm{d}t} $$
所以我们可以得到两空间回旋面积之比
$$ \frac{A_{k}}{A_{r}} = \left(\frac{eB}{\hbar}\right)^{2} $$
所以可以得到倒空间中回旋面积
$$ A_{k} = \frac{2\pi eB}{\hbar}(n + \gamma) $$
这就是倒空间中的轨道量子化条件.
若保持回旋面积 $A_{k}$ 不变, 变换一下公式形式:
$$ \frac{1}{B} = \frac{2\pi e}{\hbar A_{k}}(n + \gamma) $$
所以
$$ \Delta\left(\frac{1}{B}\right) = \left(\frac{1}{B_{n+1}} - \frac{1}{B_{n}}\right)\\ = \frac{2\pi e}{\hbar}\frac{1}{A_{k}} $$
所以只要测得物理量 $B^{-1}$ 的变化周期, 我们就可以得到倒空间中电子的回旋面积 $A_{k}$.
de Hass-Van Alphen 效应
考虑二维情形且忽略自旋, 即有
这种振荡以 $\frac{1}{B}$ 为周期. 且
$$ \Delta\left(\frac{1}{B}\right) = \frac{2\pi e}{\hbar} \cdot\frac{1}{A_{k_{F}}} $$
其中 $A_{k_{F}}$ 的示意图:
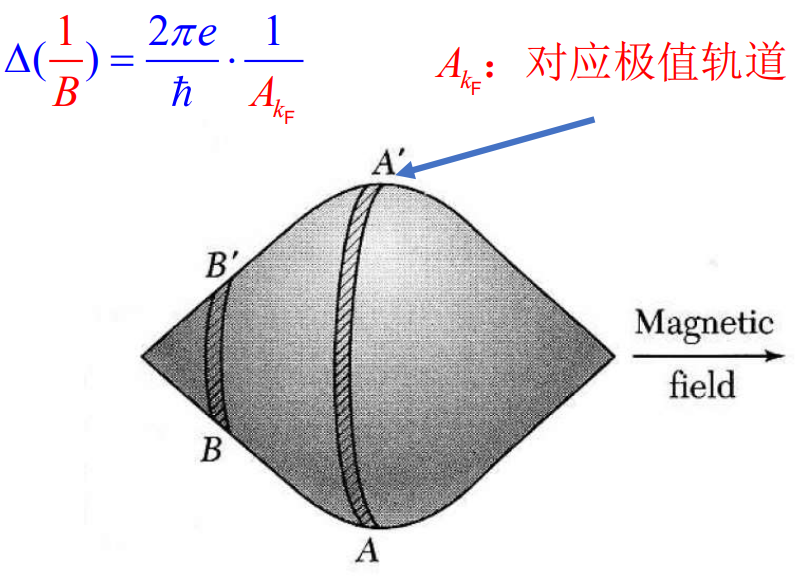
对于金银铜这样的 fcc 结构, 它们都只有一个价电子, 所以其费米面相似.
电子浓度都为
$$ n = \frac{4}{a^{3}} $$
所以自由电子的费米球半径 $k_{F}$ 即为
$$ k_{F} = \left(3\pi^{2}n\right)^{\frac{1}{3}} = \left(\frac{12\pi^{2}}{a^{3}}\right)^{\frac{1}{3}}\approxeq 4.90 a^{-1} $$
跨越布里渊区所需要的最短距离为
$$ \sqrt{3} b = \left(\frac{2\pi}{a}\right)\approxeq 10.88a^{-1} $$
布里渊区相对的小正方形之间的距离为
$$ \frac{4\pi}{a}\approxeq 12.57a^{-1} $$
对于金, 令磁场方向变化范围很大, 则测得
$$ \Delta\left(\frac{1}{B}\right) = 2\times 10^{-9} \text{G}^{-1} $$
所以可以反推其极值轨道面积
$$ S = \frac{2\pi e}{\hbar}\cdot\left[\Delta\left(\frac{1}{B}\right)\right]^{-1}\approxeq 4.8\times 10^{16}\text{cm}^{-2} $$
而金的自由电子费米球的极值面积约为 $4.5\times 10^{16}\text{cm}^{-2}$, 两者相差已经到了小数位了.
磁场下的二维体系电子
根据前面的计算, 我们已经知道了
- 三维 $$ E = \frac{p_{z}^{2}}{2m} + \left(n + \frac{1}{2}\right)\hbar\omega_{c} $$
- 二维 $$ E = \left(n + \frac{1}{2}\right)\hbar\omega_{c} $$
显然, 对于二维电子而言, 其能量分布是分立的, 如果将其绘制在 $E-g(E)$ 图上, 大致会呈现出这样的效果:
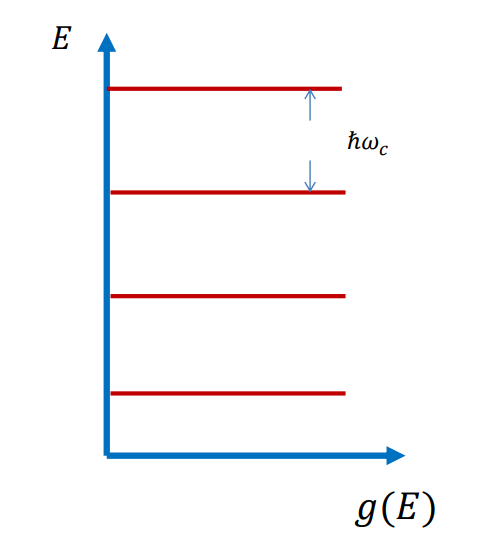
但是经历过峰分析的训练, 我们就知道任何峰都会有一定程度的展宽. 接下来我们就要推导朗道能级的展宽.
朗道能级的展宽
本征展宽
本征展宽都是通过不确定度关系推导出来的. 因为电子在磁场中做回旋运动, 所以会存在弛豫时间 $\tau$, 所以就存在关系式
$$ \delta E \approx \frac{\hbar}{\tau} $$
根据该关系式, 可知如果使得朗道能级彼此之间明确分离, 就要求弛豫时间足够长, 即 $$ \omega_{c}\cdot\tau \gg 1 $$ 这样才会有确定的朗道能级.
温度展宽
在常规温度下($T>0$), 任何能级都会因为温度而产生一定程度的展宽.
如果要让朗道能级明确分离, 就需要满足关系式
$$ \hbar\omega_{c} > k_{B}T $$
这也暗示着, 要在低温极限下才能够观察到分离状态的朗道能级.
简并度
在固体物理中, 我们也将简并度称为单位面积内每个朗道能级的电子数.
所以我们可以得到单位面积内朗道能级的简并度为
$$ n_{L} = \frac{2eB}{h} $$
对单位面积内总电子数, 有
- 电导极小时(即态密度的波谷)
$$ N_{L} = n\frac{2eB}{h} $$
- 电导极大时(即态密度的波峰)
$$ N_{L} = \left(n + \frac{1}{2}\right)\frac{2eB}{h} $$
所以电导的振荡周期为
$$ \Delta\left(\frac{1}{B}\right) = \frac{2e}{hN_{L}} $$
霍尔效应
电导率张量为
$$ \overleftrightarrow{\sigma} = \frac{\sigma_{0}}{1+(\omega_{c}\tau)^{2}} \begin{bmatrix} 1 & -\omega_{c}\tau \\ \omega_{c}\tau & 1 \end{bmatrix} $$
霍尔系数
$$ R_{H} = \frac{E_{y}}{j_{x}B} = \frac{\sigma_{xy}}{\sigma_{xx}^{2} + \sigma_{xy}^{2}}\cdot\frac{1}{B}\\ = \frac{-1}{B}\cdot\frac{\omega_{c}\tau}{\sigma_{0}} = -\frac{1}{ne} $$
当 $\omega_{c}\tau \gg 1$, 即有 $\sigma_{xy}\gg\sigma_{xx}$
对于二维各向同性体系, 写出
$$ \begin{bmatrix} J_{x}\\ J_{y} \end{bmatrix}= \begin{bmatrix} \sigma_{xx} & \sigma_{xy}\\ -\sigma_{xy} & \sigma_{yy} \end{bmatrix} \begin{bmatrix} E_{x}\\ E_{y} \end{bmatrix} $$
这实际上是一个方程组:
$$ J_{x} = \sigma_{xx}E_{x} + \sigma_{xy}E_{y}\\ J_{y} = -\sigma_{xy}E_{x} + \sigma_{yy}E_{y} $$
当考虑霍尔效应时, 即 $J_{y} = 0$. 于是得到
$$ \rho_{xx} = \frac{E_{x}}{J_{x}} = \frac{\sigma_{xx}}{\sigma_{xx}^{2} + \sigma_{xy}^{2}}\\ \rho_{xy} = \frac{E_{y}}{J_{x}} = \frac{\sigma_{xy}}{\sigma_{xx}^{2} + \sigma_{xy}^{2}} $$
如果有 $\omega_{c}\tau\gg 1$, 这就代表电子在实空间中只会在很小范围内转圈, 不会产生定向运动. 即有
$$ \sigma_{xy} \gg \sigma_{xx} $$
我们可以将 $\rho_{xx}, \rho_{xy}$ 分母部分进行简化:
$$ \lim_{\frac{\sigma_{xy}}{\sigma_{xx}}\rightarrow\infty}\rho_{xx} = \frac{\sigma_{xx}}{\sigma_{xy}^{2}}\\ \lim_{\frac{\sigma_{xy}}{\sigma_{xx}}\rightarrow\infty}\rho_{xy} = \frac{1}{\sigma_{xy}} = R_{H}B $$
$R_{H} = \frac{E_{y}}{J_{x}B}$
电阻
在周期性势场下的电子是布洛赫波, 而布洛赫波不会产生衰减, 所以 $T = 0$ 的完美晶体在不考虑电子-电子相互作用的情况下是没有电阻的.
电阻的主要来源是周期性势场的不完美(晶格热运动, 晶格缺陷…)
电子-声子散射对电导的作用
- 只有费米面附近 $k_{B}T$ 的电子才会参与;
- 能量守恒: $$ E_{k’} = E_{k} \pm \hbar\omega $$
- 动量守恒: $$ \vec{k}’ =\vec{k} \pm\vec{q} + \vec{G} $$
- 声子能量 $\approx k_{B}T\approx \text{meV}$; 电子费米能量 $\approx \text{eV}$
通常 $E_{k}\gg\hbar\omega$, 所以电子-声子散射可以被近似为准弹性散射.
我们用下面这张图来描述电子-声子散射过程:
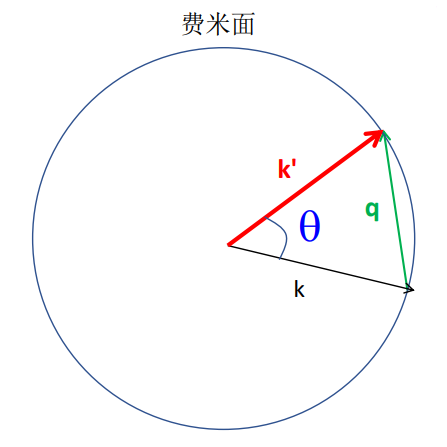
我们可以根据上图总结出以下要点:
- 电子初态为 $\mathbf{k}$ 方向的运动;
- 电子从 $\mathbf{k}$ 散射到 $\mathbf{k}’$, 这导致了电阻的增加;
- 散射前后, 电子都在费米面上;
- 散射产生的波矢变化为 $\mathbf{q}$ (即声子);
- $\theta$ 越大, 该散射对电阻的贡献越大.
弛豫时间 $\tau$ 与 散射概率之间的关系:
$$ \frac{1}{\tau} = \left(\frac{1}{2\pi}\right)^{3}\int\underbrace{\omega_{\vec{k}, \vec{k}’}}_{\text{电子被声子从}\vec{k}{散射到}\vec{k}’\text{的概率}}(1-\cos{\theta})\mathrm{d}\vec{k}' $$
高温
在 $T > \Theta_{D}$ 时, 所有高频声子都被激发. 而声子动量 $\mathbf{q}$ 又足够大, 所以大角度的散射将会占主导.
在高温下, 可以将散射动量 $\mathbf{q}$ 近似为与温度无关. 而散射概率线性正比于声子数目, 声子数目在高温下又线性正比于温度, 所以我们可以用如下关系式来描述:
$$ \rho\propto\frac{1}{\tau}\propto T(\text{高温}) $$
低温
低温下能够激发的声子动量将会远小于 $k_{F}$, 即有
$$ q\ll k_{F}, $$
所以就有 $\theta$ 很小.
根据德拜相关结论, 我们可以知道 $T^3$ 率:
$$ N_{\text{声子}} \propto T^{3}(\text{低温}) $$
所以我们有
$$ 1-\cos{\theta} = 2\sin^{2}\left(\frac{\theta}{2}\right) = \frac{1}{2}\left(\frac{q}{k_{F}}\right)^{2}(\theta\text{很小}) $$
所以我们得到低温极限条件:
$$ q\approx E \approx k_{B}T\\ 1-\cos{\theta}\approx T^{2}\\ \omega_{\vec{k},\vec{k}’}\propto T^{3} $$
所以我们就有了
$$ \rho\propto \frac{1}{\tau}\propto T^{5} $$
下图描述的是倒逆散射过程, 即费米面之间的转移.
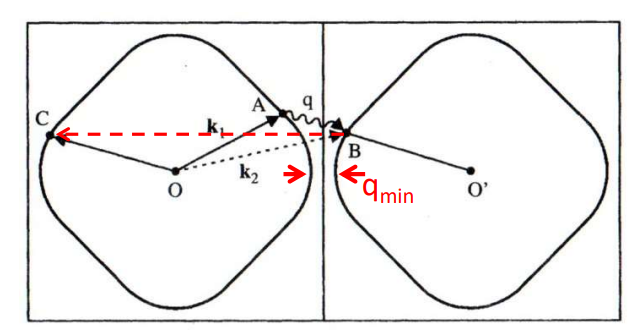
通过一个很小的声子波矢 $\mathbf{q}$, 就可以使电子从第一布里渊区的 $A$ 点散射到了其相邻布里渊区中的 $B$ 点.
根据周期性条件, $B$ 可以通过一个倒格矢映射到原本第一布里渊区中的某点 $C$, 所以综合下来看, 相当于电子通过一个很小的声子波矢 $\mathbf{q}$实现了一个大角度的散射(U-process).
在真正极低温下, 声子贡献其实已经接近于0, 电阻率的主要部分将来自于电子-电子相互作用而因此正比于 $T^{2}$, 这种物质现象被称作费米液体.
剩余电阻率
使用极限的方法来思考这个问题. 当温度非常接近 $0$ 的时候, 电阻率将由谁来贡献?
- 声子贡献 $\rightarrow 0$;
- 电子贡献 $\rightarrow 0$;
- 杂质贡献.
所以我们可以确定为杂质贡献. 如果杂质没有复杂内部结构, 我们就可以确定其为弹性散射. 这将表明:
- 极低温下, 杂质原子处于基态, 而激发态与基态能量差很大;
- 杂质和电子无法交换能量;
- 杂质浓度不随温度变化;
- 电子和杂质之间的散射势也不随温度变化.
既然电子和杂质散射产生的电阻和温度因素无关, 就有
$$ \left(\frac{\partial \rho}{\partial T}\right)_{T\rightarrow 0} = 0\Rightarrow \rho_{T\rightarrow 0} = \textit{const.} $$
磁阻
磁阻是电阻随着磁场的变化.
理想状态
因为只有一种载流子, 具有完美球形费米面的体系中, 洛伦兹力将会与电场力平衡, 电子的运动将对是否有磁场不敏感, 所以不会有磁阻.
真实情况
实际的金属当然是有磁阻的, 这说明上面的一些条件遭到了破坏.
-
只有一条能带经过了费米能级, 但是费米能级并不是严格的球形, 所以费米速度, 有效质量, 弛豫时间出现了各向异性;
-
有多条能带都经过了费米能级, 且每条能带的费米速度, 有效质量, 弛豫时间等各不相同.
比如我们考虑两条各向同性的能带, 就有
$$ \frac{\Delta\sigma}{\sigma_{0}} = -\frac{\sigma_{10}\sigma_{20}}{(\sigma_{10} + \sigma_{20})^{2}} (\omega_{c1}\tau_{1} - \omega_{c2}\tau_{2})^{2}\\ \Rightarrow \frac{\Delta \rho}{\rho_{0}} = \frac{\rho(B) - \rho(0)}{\rho(0)}\propto B^{2}>0 $$
在某些情况下, 可能会在低温出现负磁阻.
相位效应
相位相干
电子在输运过程中会有两种散射类型发生:
-
弹性散射(杂质)$\tau_{1}$ 波矢:$\vec{k}\rightarrow\vec{k}’(|\vec{k}| = |\vec{k}’|)$; 相位:$\phi\rightarrow\phi’$($\phi$和 $\phi’$ 之间存在确定关系)即电子是相干的;
-
非弹性散射(声子)$\tau_{2}$ 电子非相干, 因为 $\phi = e^{-iEt/h}$
在低温下, $\tau_{2}\gg\tau_{1}$. 所以低温下电子能够保持很长时间的相干性.
相位相干长度
$$ l_{\phi} = v_{F}\tau_{2} $$ 在足够低温时, 该长度甚至可以达到微米量级.
从 $x’$ 到 $x’’$, 存在着无穷多的路径. 我们可以将其概括为
$$ A_{i} = |A_{i}|e^{i\phi_{i}} $$
所以我们可以写出从 $x’$ 到 $x’’$ 的总概率为
$$ P = |\sum_{i}A_{i}|^{2} = |\sum_{i}A_{i}^{2}| + \underbrace{\sum_{i\neq j}A_{i}A_{j}}_{=0} $$
假设存在一个环 $A-B-C$, 那么 $A-B-C-A$ 和 $A-C-B-A$ 两个路径对应的概率幅相同, 分别用 $A_{+}$ 和 $A_{-}$ 来描述.
所以在 $A$ 点发现有电子的概率为
$$ P = |A_{+}|^{2} + |A_{-}|^{2} + A_{+}A_{-}^{*} + A_{+}^{*}A_{-} = 4A^{2} $$
然而在经典情况下, 在 $A$ 点找到电子的概率为 $P’ = 2\cdot A^{2} = 2A^{2}$, 这说明电子有更大的概率回到起点, 或者更低的概率离开起点.
这种效应会导致电导变小, 电阻增大. 这种效应被称作弱局域化现象.
在低温时, 弱局域化(WL)会导致电阻按照对数方式上升 二维系统: $$ \Delta\sigma = -\sigma_{00}\ln{\frac{\tau_{2}}{\tau_{1}}} = \sigma_{00}p\ln{T} $$
负磁阻
已知 $\vec{B} = \nabla\times\vec{A}$, 所以有单电子薛定谔方程解
$$ \varphi(\vec{r}) = \varphi_{0}(\vec{r}) = e^{-\frac{ie}{\hbar}\int \vec{A}(\vec{r}’)\cdot\mathrm{d}\vec{r}’} $$
所以磁场会使得路径产生附加的相位
比如前面 $A-B-C$ 闭合路径的例子中, 即有
$$ A_{+}\rightarrow A_{+}e^{-\frac{ie}{\hbar}\oint\vec{A}\cdot\mathrm{d}\vec{l}} = A_{+}e^{-\frac{ie}{\hbar}\iint\vec{B}\cdot\mathrm{d}\vec{S}} = A_{+}e^{-\frac{ie}{\hbar}\Phi}\\ A_{-}\rightarrow A_{-}e^{\frac{ie}{\hbar}\Phi} = A_{-}e^{i2\pi \Phi/(2\Phi_{0})} $$
$\Phi_{0} = \frac{h}{2e}$, 为磁通量子.
所以在 $A$ 点发现有电子存在的概率为
$$ P = 2A^{2}\left[1 + \cos^{2}{\left(2\pi\frac{\Phi}{\Phi_{0}}\right)}\right]\leq 4A^{2} $$
如果存在很强的自旋-轨道耦合, 就会出现弱-反局域化现象, 也就是正磁阻现象.
输运现象
不均匀性会导致物理量的流动.
温度:$\vec{J}_{Q} = -\kappa\nabla T$;
浓度:$\vec{J}_{Q} = -D\nabla n$;
电势:$\vec{J}_{e} = -\sigma\nabla\varphi$
我们引入非平衡分布函数来描述输运现象.
$$ f_{n}(\vec{r},\vec{k},t)\frac{\mathrm{d}\vec{r}\mathrm{d}\vec{k}}{(2\pi)^{3}} $$
上式表示的是, 单位体积的材料中, 在 $t$ 时刻的第 $n$ 个能带中, 在相空间 $\left(\vec{r},\vec{k}\right)$ 处单位体积 $\mathrm{d}\vec{r}\mathrm{d}\vec{k}$ 某自旋的平均电子数.
非平衡分布函数的电流表示
先只考虑一条能带, 那么就有电流密度
$$ \vec{J}_{e} = -en(\vec{r},t)\vec{v}_{d}\\ = -\frac{2}{(2\pi)^{3}}\int e\vec{v}_{\vec{k}}\color{red}{f\left(\vec{r},\vec{k},t\right)}\mathrm{d}\vec{k} $$
平衡态下的分布函数
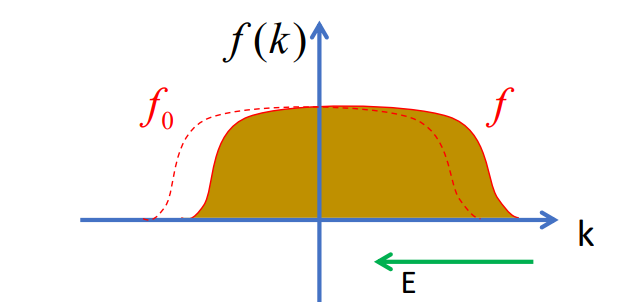
我们可以使用 $f_{0}$ 来表示平衡态下的分布函数. 对于均匀体系, $f_{0}$ 显然对位置无关.
如果不考虑外场对分布函数的影响, 而 $f_{0}$ 是对 $\vec{k}$ 的偶函数, $\vec{v}$ 是对 $\vec{k}$ 的奇函数, 所以我们可以推测
$$ \vec{J} = -\frac{2}{(2\pi)^{3}}\int e\vec{v}_{\vec{k}}f_{0}\mathrm{d}\vec{k} = 0 $$
从平衡态到非平衡态
因为有了动量移动
$$ \frac{\mathrm{d}\vec{k}}{\mathrm{d}t} = -\frac{e\vec{E}}{\hbar} $$
所以之前 $f_{0}$ 的对称性遭到破坏, 即
$$ f(\vec{k}) \neq f(-\vec{k}) $$
因此电流密度将有 $$ \vec{J} = -\frac{2}{(2\pi)^{3}}\int e\vec{v}_{\vec{k}}f\mathrm{d}\vec{k}\neq 0 $$
如果用图像来表示这种平衡态到非平衡态的变化, 即为下图所示:
玻尔兹曼方程
假定系统处于局部平衡状态
- 系统总体呈现非平衡状态;
- 每一个宏观小, 但是微观上足够大的区域是平衡态.
我们就可以将分布函数的改变分成两个部分:
$$ \frac{\partial f}{\partial t} = \left(\frac{\partial f}{\partial t}\right)_{\text{漂移}} + \left(\frac{\partial f}{\partial t}\right)_{\text{碰撞}} $$
漂移(无碰撞)
根据连续性方程, 即有
$$ \underbrace{f\left(\vec{r},\vec{k},\vec{t}\right)}_{t\text{时刻的电子}} = \underbrace{f\left(\vec{r}-\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\mathrm{d}t, \vec{k} - \frac{\mathrm{d}\vec{k}}{\mathrm{d}t}\mathrm{d}t, t - \mathrm{d}t\right)}_{t-\mathrm{d}t\text{时刻的电子}} $$
漂移 $\oplus$ 碰撞
$$ f\left(\vec{r},\vec{k},\vec{t}\right) = f\left(\vec{r}-\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\mathrm{d}t, \vec{k} - \frac{\mathrm{d}\vec{k}}{\mathrm{d}t}\mathrm{d}t, t - \mathrm{d}t\right) + \left(\frac{\partial f}{\partial t}\right)_{\text{碰撞}}\mathrm{d}t $$
我们可以写出这个方程的微分形式:
为了节省篇幅, 使用 $$ \frac{\mathrm{d}A}{\mathrm{d}t} = \dot{A} $$
$$ \frac{\partial f}{\partial t} = -\dot{\vec{k}}\cdot\frac{\partial f}{\partial\vec{k}} - \dot{\vec{r}}\cdot\frac{\partial f}{\partial\vec{r}} + \left(\frac{\partial f}{\partial t}\right)_{\text{碰撞}} $$
这样我们就得到了玻尔兹曼方程.
如果我们取进一步的稳态条件 $\partial_{t}f = 0$, 我们就可以得到电子的稳态玻尔兹曼方程
$$ \boxed{\dot{\vec{k}}\cdot\frac{\partial f}{\partial\vec{k}} + \dot{\vec{r}}\cdot\frac{\partial f}{\partial\vec{r}} = \left(\frac{\partial f}{\partial t}\right)_{\text{碰撞}}} $$
$\dot{\vec{k}}$ 和外加电磁场有关;
$\dot{\vec{r}} = \frac{1}{\hbar}\nabla_{\vec{k}}\epsilon_{\vec{k}}$ 由能带自身结构决定.
近似处理
- 产生的非平衡偏移极小
$$ f = f_{0} + f_{1} (f_{1}\ll f_{0}) $$
- 碰撞弛豫时间近似
$$ \left(\frac{\partial f}{\partial t}\right) = \frac{f_{0} - f}{\tau} = -\frac{f_{1}}{\tau} $$
所以就有了近似条件
$$ \frac{\partial f}{\partial\vec{k}} = \frac{\partial f_{0}}{\partial\vec{k}} + \frac{\partial f_{1}}{\partial\vec{k}} \approx \frac{\partial f_{0}}{\partial\vec{k}}\\ \frac{\partial f}{\partial\vec{r}} = \frac{\partial f_{0}}{\partial\vec{r}} + \frac{\partial f_{1}}{\partial\vec{r}} \approx \frac{\partial f_{0}}{\partial\vec{r}}\\ $$
所以原本的玻尔兹曼方程特化为
$$ \dot{\vec{k}}\cdot\frac{\partial f_{0}}{\partial\vec{k}} + \dot{\vec{r}}\cdot\frac{\partial f_{0}}{\partial\vec{r}} = -\frac{f_{1}}{\tau} $$
直流电导率
如果只存在电场, 那么我们可以写出
$$ -\frac{e\vec{E}}{\hbar}\cdot\frac{\partial f_{0}}{\partial\vec{k}} = -\frac{f_{1}}{\tau} $$
所以我们可以求解
$$ \vec{J}_{e} = -\frac{2e}{(2\pi)^{3}}\int f\vec{v}_{\vec{k}}\mathrm{d}\vec{k} = -\frac{e}{4\pi^{3}}\int(f_{0}+f_{1})\vec{v}_{\vec{k}}\mathrm{d}\vec{k}\\ = -\frac{e}{4\pi^{3}}\int f_{1}\vec{v}_{\vec{k}}\mathrm{d}\vec{k} $$
而我们已经知道
$$ f_{1} = \frac{e\tau\vec{E}}{\hbar}\cdot\frac{\partial f_{0}}{\partial\vec{k}};\\ \frac{\partial f_{0}}{\partial\vec{k}} = \frac{\partial f_{0}}{\partial\epsilon}\cdot\frac{\partial\epsilon}{\partial\vec{k}}\\ \vec{k} = \frac{1}{\hbar}\frac{\partial\epsilon}{\partial\vec{k}} $$
使用这些条件, 得到电流密度
$$ \vec{J}_{e} = \frac{e^{2}}{4\pi^{3}}\int\tau\color{red}{\frac{\partial f_{0}}{\partial\epsilon}}\vec{k}_{\vec{k}}(\vec{v}_{\vec{k}}\cdot\vec{E})\mathrm{d}\vec{k}\\ = \frac{e^{2}}{4\pi^{3}}\int\tau\frac{\vec{v}_{\vec{k}}(\vec{v}_{\vec{k}}\cdot\vec{E})}{\hbar v_{k}}\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)\mathrm{d}S\mathrm{d}\epsilon $$
将 $k$ 空间中的体积分转换为了等能面的面积分.
$\color{red}{\frac{\partial f_{0}}{\partial\epsilon}}$ 相当于费米能量处的 $\delta$ 函数
所以进一步化简得到
$$ \vec{J}_{e} = \frac{e^{2}}{4\pi^{3}\hbar}\int\tau\frac{\vec{v}_{k}(\vec{v}_{\vec{k}}\cdot\vec{E})}{v_{k}}\color{red}{\mathrm{d}S_{F}} $$
$\color{red}{\mathrm{d}S_{F}}$ 表示在费米面上进行面积分.
我们已有的电学知识知道
$$ \vec{J}_{e} = \overleftrightarrow{\sigma}\cdot\vec{E} $$
所以我们也将上面的公式整理作张量形式:
$$ \vec{J}_{e} = \underbrace{\left[\frac{e^{2}}{4\pi^{3}\hbar}\int\tau\frac{\vec{v}_{\vec{k}}\vec{v}_{\vec{k}}}{v_{k}}\mathrm{d}S_{F}\right]}_{\text{张量}\overleftrightarrow{\sigma}}\cdot\vec{E} $$
因为三个方向完全一致, 所以根据对称性将张量简化为标量:
$$ \sigma=\sigma_{xx}=\sigma_{yy}=\sigma_{zz} = \frac{1}{3}\left(\sigma_{xx}+\sigma_{yy}+\sigma_{zz}\right) $$
而单独方向的
$$ \sigma_{xx} = \frac{e^{2}}{4\pi^{3}\hbar}\int\tau\frac{v_{k_{x}}^{2}}{v_{k}}\mathrm{d}S_{F} = \frac{1}{12\pi^{3}}\frac{e^{2}}{\hbar}\int\tau v_{k}\mathrm{d}S_{F} $$
如果再加上补充条件有效质量 $m^{*}$ 以及 $\tau$ 各向同性, 就可以进一步得到
$$ \sigma = \frac{\tau}{12\pi^{3}}\frac{e^{2}}{m^{*}}\int k_{F}\mathrm{d}S_{F} $$
考虑最简单的费米面(球面), 即有
$$ \sigma = \frac{\tau}{3\pi^{2}}\frac{e^{2}k_{F}^{3}}{m^{*}} $$
载流子浓度为 $n$, 费米波矢为 $k_{F}$, 即有 $$ n = \frac{N}{V} = \frac{2}{V}\cdot\frac{4}{3}\pi k_{F}^{3}\cdot\frac{V}{(2\pi)^{3}} = \frac{k_{F}}{3\pi^{2}} $$
即有结论
$$ \sigma = \frac{ne^{2}\tau_{E_{F}}}{m^{*}} $$
正是 Drude Model.
热电势
观察推导得到的玻尔兹曼方程:
$$ \dot{\vec{k}}\cdot\frac{\partial f_{0}}{\partial\vec{k}} + \dot{\vec{r}}\cdot\color{red}{\frac{\partial f_{0}}{\partial\vec{r}}} = -\frac{f_{1}}{\tau} $$
如果温度因素介入, 当然要考虑温度对材料中 $f_{0}$ 的影响.
$$ \dot{\vec{r}}\cdot\frac{\partial f_{0}}{\partial\vec{r}} = \dot{\vec{r}}\cdot\left(\frac{\partial f_{0}}{\partial T}\nabla T + \frac{\partial f_{0}}{\partial\mu}\nabla\mu\right) $$
- 温度 $$ \frac{\partial f_{0}}{\partial T} = -\frac{\partial f_{0}}{\partial\epsilon}\cdot\frac{\epsilon-\mu}{T} $$
- 化学势 $$ \frac{\partial f_{0}}{\partial\mu} = -\frac{\partial f_{0}}{\partial\epsilon} $$
代入上述化简条件, 即可得到无电场下的方程
$$ -\frac{\partial f_{0}}{\partial\epsilon}\vec{v}_{\vec{k}}\cdot\left[\frac{\epsilon_{k}-\mu}{T}\nabla T + \nabla\mu\right] = -\frac{f_{1}}{\tau} $$
类比前面得出电流密度的方法,
$$ \vec{J}_{e} = -\frac{e}{4\pi^{3}}\int f_{1}\vec{v}_{\vec{k}}\mathrm{d}\vec{k} $$
我们也可以通过这个分布函数得到电流密度
$$ \vec{J}_{e} = \frac{e}{4\pi^{3}}\int\tau\frac{(\vec{v}_{\vec{k}}\vec{v}_{\vec{k}})\cdot\color{red}{\nabla\mu}}{\hbar v_{k}}\color{red}{\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)}\mathrm{d}S\mathrm{d}\epsilon + \frac{e}{4\pi^{3}}\int\tau\frac{(\vec{v}_{\vec{k}}\vec{v}_{\vec{k}})\cdot\color{red}{\nabla T}}{\hbar v_{k}}\left(\frac{\epsilon - \mu}{T}\right)\color{red}{\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)}\mathrm{d}S\mathrm{d}\epsilon $$
可以看到 $\nabla T$ 能够产生定向电流, 因此被称为热电效应.
我们对比有电场和无电场两个公式的区别:
$$ \vec{J}_{e} = \frac{e^{2}}{4\pi^{3}}\int\tau\frac{(\vec{v}_{\vec{k}}\vec{v}_{\vec{k}})\cdot\color{red}{\frac{\nabla\mu}{e}}}{\hbar v_{k}}\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)\mathrm{d}S\mathrm{d}\epsilon + \frac{e}{4\pi^{3}}\int\tau\frac{(\vec{v}_{\vec{k}}\vec{v}_{\vec{k}})\cdot\nabla T}{\hbar v_{k}}\left(\frac{\epsilon - \mu}{T}\right)\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)\mathrm{d}S\mathrm{d}\epsilon\\ \vec{J}_{e} = \frac{e^{2}}{4\pi^{3}}\int\tau\frac{(\vec{v}_{\vec{k}}\vec{v}_{\vec{k}})\cdot\color{red}{\vec{E}}}{\hbar v_{k}}\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)\mathrm{d}S\mathrm{d}\epsilon $$
可以观察到化学势梯度 $\color{red}{\frac{\nabla\mu}{e}}$ 与外场电场 $\color{red}{\vec{E}}$ 等价, 所以测得的电场实际上已经包含了热电效应.
热流
综合考虑外部电场和温度等因素, 我们得到表达式
$$ \vec{J}_{e} = \frac{e^{2}}{4\pi^{3}}\int\tau\frac{(\vec{v}_{\vec{k}}\vec{v}_{\vec{k}})\cdot\left(\color{red}{\vec{E} + \frac{\nabla\mu}{e}}\right)}{\hbar v_{k}}\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)\mathrm{d}S\mathrm{d}\epsilon + \frac{e}{4\pi^{3}}\int\tau\frac{(\vec{v}_{\vec{k}}\vec{v}_{\vec{k}})\cdot\nabla T}{\hbar v_{k}}\color{red}{\left(\frac{\epsilon-\mu}{T}\right)}\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)\mathrm{d}S\mathrm{d}\epsilon $$
类比于电流密度, 我们可以尝试写出热流密度的表达式. 单个电子携带的热量相当于溢出化学势的额外能量 $\epsilon_{k} - \mu$, 所以热流密度的原始定义为
$$ \vec{J}_{Q} = \frac{1}{4\pi^{3}}\int(\epsilon_{k} - \mu)\vec{v}_{k} f_{1}\mathrm{d}\vec{k} $$
讨论过程都是相同的, 所以我们需要做的就是将原本的电荷 $e$ 换为 $\epsilon_{k} - \mu$.
即有
$$ \vec{J}_{Q} = -\frac{e}{4\pi^{3}}\int\color{red}{\vec{E}}\cdot\left[\tau\frac{(\vec{v}_{\vec{k}}\vec{v}_{\vec{k}})\color{red}{(\epsilon_{k} - \mu)}}{\hbar v_{k}}\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)\mathrm{d}S\mathrm{d}\epsilon\right] - \frac{1}{4\pi^{3}}\int\color{red}{\nabla T}\cdot\left[\tau\frac{(\vec{v}_{\vec{k}}\vec{v}_{\vec{k}})}{\hbar v_{k}}\color{red}{\frac{(\epsilon - \mu)^{2}}{T}}\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)\mathrm{d}S\mathrm{d}\epsilon\right] $$
这样冗长的积分表达非常麻烦, 我们引入一个积分简写式
$$ \zeta_{n} = \frac{\tau}{12\pi^{3}\hbar}\int v_{k}\color{red}{(\epsilon_{k} - \mu)^{n}}\left(-\frac{\partial f_{0}}{\partial\epsilon}\right)\mathrm{d}S\mathrm{d}\epsilon $$
所以电流密度和热流密度有更简单的表达方式
$$ \vec{J}_{e} = e^{2}\zeta_{0}\color{red}{\vec{E}} - \frac{e}{T}\zeta_{1}(\color{red}{-\nabla T})\\ \vec{J}_{Q} = -e\zeta_{1}\color{red}{\vec{E}} + \frac{1}{T}\zeta_{2}(\color{red}{-\nabla T}) $$
其实这里有未提及的假设, 即热与电的弛豫时间是相同的.
如果不存在外加电场而只有温度梯度, 即有
$$ \vec{J}_{e} = 0\Rightarrow e^{2}\zeta_{0}\vec{E} - \frac{e}{T}\zeta_{1}(-\nabla T) = 0 $$
那么存在温度梯度导致的电场
$$ \vec{E} = \frac{1}{eT}\frac{\zeta_{1}}{\zeta_{0}}(-\nabla T) $$
所以热流密度为
$$ \vec{J}_{Q} = \frac{1}{T}\left(\zeta_{2} - \frac{\zeta_{1}^{2}}{\zeta_{0}}\right)(-\nabla T) $$
所以根据 $\vec{J}_{Q} = \kappa(-\nabla T)$, 得到
- 热导率
$$ \kappa = \frac{1}{T}\left(\zeta_{2} - \frac{\zeta_{1}^{2}}{\zeta_{0}}\right)\\ \sigma = e^{2}\zeta_{0} $$
以上结论均建立在 热电弛豫时间相同 的假设上, 但是实际上两者未必相同.W
热电势
上面我们知道了温度梯度也会产生电场, 我们将其写作
$$ \vec{E} = \frac{1}{eT}\frac{\zeta_{1}}{\zeta_{0}}(-\nabla T) $$
我们可以定义热电系数(Thermopower), 其含义为单位温度差下材料中电势差的变化量.
$$ \vec{E} = \color{red}{S}\nabla T $$
所以
$$ \color{red}{S} = -\frac{1}{eT}\frac{\zeta_{1}}{\zeta_{0}} = -\frac{\pi^{3}}{3}\frac{k_{B}^{2}T}{e}\left[\frac{\partial\ln{\sigma}}{\partial\epsilon}\right]_{E_{F}} $$
因为
$$ \sigma\propto\int\tau v_{k}\mathrm{d}S $$
所以有
$$ S \propto T\left(\frac{\partial\ln{\langle\tau\rangle}}{\partial\epsilon} + \frac{\partial\ln{\langle v_{k}\rangle}}{\partial\epsilon} + \frac{\partial\ln{S}}{\partial\epsilon}\right)_{E_{F}} $$