开题准备
流程手续
-
课题名称:
-
课题性质:论文
-
课题来源:
-
项目编号:
-
其他:颗粒物质关键物理问题实验研究
-
其他指导老师: 无
-
毕业论文基本内容和要求:
-
计划进度行数:
-
2023年10月至2023年11月 进行系统的文献调研,了解相关背景,掌握理论基础并确立实验具体方案
-
2023年11月至2023年12月 设计实验方案,设计并搭建实验装置,选取合适的实验颗粒,做好实验准备工作。
-
2024年1月至2024年4月 开始进行实验,分析、调整并改进实验参数,得到成套数据并进行分析。
-
2024年4月至2024年5月 通过模拟验证实验结果
-
2024年6月 运用理论解释实验结果,完善实验数据,撰写毕业论文
- 课题研究目的和意义(含国内外研究现状综述):
颗粒物质体系是指由直径大于 1 微米的粒子形成的离散集合, 包括土壤, 沙石等建筑材料, 谷物, 咖啡豆等农产品, 煤炭和铁矿石等矿产品, 化工原料和医用制药原料等. 每年在工业上处理颗粒物质原材料需要耗费的世界能源需要占据生产总能源的 10%, 然而目前处理颗粒物质的工业设备不仅操作效率远低于其设计效率, 而且时常有灾难性事故发生. 除此之外, 沙尘暴, 雪崩, 地震, 泥石流等自然现象和地质灾害业余颗粒物质紧密联系在一起. 因此, 任何有关颗粒材料新的物理认知和发现都与人类的生产活动息息相关, 可以对世界经济发展产生重要影响.
颗粒物质体系是典型的非平衡态体系, 涉及塑性形变, 雪崩效应, 固液相变等多种复杂行为, 但是目前已经发展出相当的统计方法和局部研究对其动力学机制进行研究. 基于 X 射线成像以及衍生的超快同步辐射 X 光成像技术对颗粒物质的研究也已经比较成熟, 但是使用 X 射线研究颗粒物质也存在部分问题: 在研究涉及微粒表面尺度的摩擦机制时, X 射线成像不足以给出局部结构的数据信息. 然而, 以贾小平为代表的研究者们在使用超声波对探测颗粒物质体系的动力学机制已经有了相当的经验, 将两者有效结合起来将有助于对颗粒物质体系有更深入的理解.
- 课题研究内容
将超声波探测研究颗粒物质堆积体系的技术和 CT(X射线) 成像技术有效结合, 从而对其三维内部结构进行分析. 通过图像处理并计算相关局部或宏观参量来分析颗粒物质休止堆积的静态结构特征, 观测其是否存在各向异性并分析其出现原因; 进一步设计实验观测颗粒物质堆积制备过程中, 表面雪崩现象出现前后的休止角变化及结构变化, 并尝试从颗粒尺度以及接触尺度来描述雪崩现象.
- 研究方法和研究思路(技术路线)
利用超声波探测和 X 光计算机层析成像技术对颗粒物质静态堆积进行拍摄与三维重构得到结构信息;利用 Matlab 对得到的信息进行图像处理, 利用顶帽变换、底帽变换、三维空间卷积、分水岭算法等图像处理方法对颗粒与背景进行分割, 找到颗粒质心位置信息;利用径向分布函数对颗粒半径进行修正;根据颗粒位置信息计算相关物理参量, 包括:(1) 局部体积分数 (2) 进行 Voronoi 分割并根据 Voronoi 元胞的闵可夫斯基张量计算其元胞球形度; (3) Voronoi 元胞长轴的空间取向; (4) 颗粒的配位数及桥结构. 根据计算的相关参量进行分析.
- 预期研究结果
颗粒物质休止堆积的空间结构可观测到各向异性; 体积分数, Voronoi 原胞球形度与取向, 颗粒配位数等与其空间位置有关. 可能会出现沿斜面的分层现象, 或者重力方向的梯度变化.
- 计划进度安排:
2023年10月至2023年11月 进行系统的文献调研,了解相关背景,掌握理论基础并确立实验具体方案
2023年11月至2023年12月 设计实验方案,设计并搭建实验装置,选取合适的实验颗粒,做好实验准备工作。
2024年1月至2024年4月 开始进行实验,分析、调整并改进实验参数,得到成套数据并进行分析。
2024年4月至2024年5月 通过模拟验证实验结果
2024年6月 运用理论解释实验结果,完善实验数据,撰写毕业论文
- 参考文献:
[1] David Aristoff and Charles Radin. Random loose packing in granular matter. Journal of Statistical Physics, 135(1):1–23, 3 2009. [Online; accessed 2023-10-11].
[2] Richard K. Bowles and S. S. Ashwin. Edwards entropy and compactivity in a model of granular matter. Phys.Rev. E, 83:031302, Mar 2011.
[3] Yixin Cao, Xiaodan Zhang, Binquan Kou, Xiangting Li, Xianghui Xiao, Kamel Fezzaa, and Yujie Wang. A dynamic synchrotron x-ray imaging study of effective temperature in a vibrated granular medium. Soft Matter, 10(29):5398–5404, 2014. [Online; accessed 2023-10-11].
[4] X. Jia. Codalike multiple scattering of elastic waves in dense granular media. Phys. Rev. Lett., 93:154303, Oct 2004.
[5] X. Jia, C. Caroli, and B. Velicky. Ultrasound propagation in externally stressed granular media. Phys. Rev. Lett., 82:1863–1866, Mar 1999.
[6] Vincent Langlois and Xiaoping Jia. Sound pulse broadening in stressed granular media. Phys. Rev. E, 91:022205, Feb 2015.
[7] J. L´eopold`es and X. Jia. Probing intermittency and reversibility in a dense granular suspension under shear using multiply scattered ultrasound. Soft Matter, 16(47):10716–10722, 2020. [Online; accessed 2023-10-11].
[8] Zhikun Zeng, Shuyang Zhang, Xu Zheng, Chengjie Xia, Walter Kob, Ye Yuan, and Yujie Wang. Equivalence of fluctuation-dissipation and edwards’ temperature in cyclically sheared granular systems. Phys. Rev. Lett., 129:228004, Nov 2022.
[9] Hao Zhou, Xiaoping Jia, Li-Yun Fu, and Arnaud Tourin. Monte carlo simulations of ultrasound scattering and absorption in finite-size heterogeneous materials. Phys. Rev. Appl., 16:034009, Sep 2021.
[10] L. Q. Zhou, X. Jia, and Q. Ouyang. Experimental and numerical studies of noise-induced coherent patterns in a subexcitable system. Phys. Rev. Lett., 88:138301, Mar 2002.
文献调研
- Codalike Multiple Scattering of Elastic Waves in Dense Granular Media
小振幅压缩声波和剪切声波提供了一种独特的非侵入式探针,可探测实际 $3$ D 颗粒介质中力网络的结构和非线性弹性的特性。
在低频情况下,与力链的相关长度对比,颗粒介质的波长非常长,因此对于传播的波来说,颗粒介质实际上是一个均匀的连续体。
在高频率下,当波长减小到晶粒大小的数量级时,力链的空间波动引起的散射效应变得非常显著,有效接触介质不再是有效的描述。
在这种情况下,散射声波是由力链的精确结构决定的特定构型,这为研究接触网络的构型变化提供了一个灵敏的工具。
然而,迄今为止,人们仍不清楚弹性波在颗粒介质中的多重散射是否可以在经典扩散传播的框架内进行描述,例如光和声在强散射随机介质中的传播,或者是否如 Liu 和 Nagel 所言,由于存在由力链创建的少数主导路径,所有频率的声波都必须沿着这些路径通过,因此弹性波在颗粒介质中的多重散射与在其他随机介质中的多重散射有着本质区别。
解决这个问题对地震学应用也有相当大的意义,它能让我们深入了解短波声发射在断层动力学中的作用。在这封信中,我们测试了扩散近似在应力作用下高频超声波在玻璃珠堆积中传播的应用。
我们发现,通过弹性波的多重散射,可以在小长度尺度上(通常长波长相干波无法到达)推断出材料特性,如力链结构的相关长度和内部耗散。
- Probing intermittency and reversibility in a dense granular suspension under shear using multiply scattered ultrasound
含有大量颗粒的体系,如泡沫、乳液、胶体悬浮液或颗粒材料,在应力小、体积分数高时通常呈固态,反之则呈液态。当剪切应力接近屈服应力时,会出现非线性流动缺陷,也称为剪切转化区。
理论预测了流动缺陷的存在,而且在胶体玻璃、泡沫、乳液和颗粒介质等不同系统中也确实观察到了流动缺陷。在颗粒介质中,分析通常局限于流化系统、表面流动、慢速流动或二维几何形状。
在三维干燥颗粒介质中,声波通过力链网络传播,对长波相干波和多重散射尾波的分析表明,各向异性以及接触断裂和形成是剪切反转下结构变化的基本要素。
此外,多散射超声波的相关函数 $\Psi$ 的演变表明,在稳定剪切过程中,力链网络的重新排列与机械响应的间歇性之间存在明显的一致性。然而,在低压条件下,配位数会减少,而且由于力链的异质性,测量会很困难。
在这方面,在准静态条件下剪切的致密颗粒悬浮液(如惯性数消失时)是很有吸引力的系统,因为它们的机械响应与干燥情况类似(也由力链网络决定),但超声波现在很容易在液相中传播。
因此,多重散射超声波主要对颗粒(散射体)位置敏感,如扩散声波光谱法(DAWS)。在 DAWS 测量中,颗粒的随机运动(如平均传输自由路径)可通过构型平均和扩散近似散射声波时间波动的自相关函数来表征。
在此,我们将探究在低剪切速率和低压条件下,高密度颗粒悬浮液在循环和稳定剪切作用下的可逆性和间歇性。与在可能存在构型平均的颗粒流化悬浮液中进行的 DAWS 测量不同,我们将仅使用多散射超声波 $\Psi$ 的自相关函数作为对此类致密悬浮液中颗粒位置整体变化的定性估计。
循环剪切会在屈服开始时导致晶粒运动从笼式运动过渡到不可逆运动。此外,循环剪切过程中的非线性机械响应分析揭示了特定的动态,这些动态可归因于力链的压实和屈曲。
对于稳定剪切,测量扭矩的间歇性与大的去相关事件同时发生。观察到的应力下降幅度与去相关性的程度有微弱但显著的联系。
- Ultrasound Propagation in Externally Stressed Granular Media
颗粒介质显示出不同于固体或液体的有趣而不寻常的特性。对外部应力下的二维和三维静态密闭颗粒系统进行的光弹性可视化研究证明,颗粒之间的接触力分布具有很强的不均匀性,从而产生了比单个颗粒尺寸大得多的强力链。这些应力分布的特征对于了解颗粒介质的结构和机械特性非常重要,特别是在改进处理技术方面。
由于声波在弹性介质中的高效穿透力,声波为研究真实的(光学不透明或强光扩散)三维颗粒集合体提供了一种非常有用,有时甚至是独一无二的技术。通过测量声波的速度和衰减,可以灵敏地探测声波传播所经过的材料的结构和机械特性。因此,描述声音在颗粒材料中的传播是一个具有根本意义的问题。最近,Liu 和 Nagel 进行了一组涉及重力作用下声音在玻璃珠系统中传播的实验。
在这些实验中,声脉冲通过扬声器产生,并由一个与晶粒直径 $d$ 大小相当的小型传声器检测到。在低振动幅度下,时域中的典型响应包括一个急剧上升的边缘,随后是几个强烈的尖峰和一个衰减的尾部。根据飞行时间速度(约 $300\text{m/s}$)与根据总检测信号相位频谱斜率确定的群速度(约 $60\text{m/s}$)之间的巨大差异,这些作者声称在这种系统中声速的确定存在模糊性。
此外,他们还发现,声音传播对单粒热膨胀或高振幅振动激励所产生的堆积构造变化非常敏感。他们认为这是由于声音在颗粒介质中主要沿着强力链传播。
然而,在土壤力学和地球物理学中,有效介质方法(长波长描述)通常用于描述声音在颗粒介质中的传播,(压缩或剪切)声速的确定似乎不成问题。这一观察结果引出了一个基本问题:是否有可能调和这两种对声音在颗粒介质中传播的描述?
- Monte Carlo Simulations of Ultrasound Scattering and Absorption in Finite-Size Heterogeneous Materials
实验研究表明,地震(弹性)波衰减对岩石性质变化的敏感程度远高于波速的。这里的衰减指的是将地震能量转化为热能的内在(即无弹性)衰减,也称为吸收或耗散。
由于地震振幅可能受到多种因素的影响,因此测量吸收率具有挑战性。由于波束扩散、波散射和边界反射等原因,在对岩石样本进行超声波实验室实验时也会遇到这种困难。
对于准均质岩石,可以忽略波的散射。这样就可以通过弹道或反射脉冲,即相干波场来测量吸收率。然而,这些方法可能会高估异质岩石的吸收率,因为弹道波衰减也包括波长尺度异质的散射。此外,在花岗岩和辉长岩等强(多重)散射岩石中,从散射尾波信号中正确识别相干脉冲甚至具有挑战性。
在工程应用中对异质材料进行非破坏性检测时也会遇到类似的情况,在这种情况下,开发了基于超声波(或地震波)尾波的诊断方法,包括在介质不断变化的情况下使用扩散波谱学。
在此,我们研究了声学(标量)辐射传递(RT)理论中从弹道机制到扩散机制的过渡,以区分有限尺寸异质介质中超声尾波的散射和本征衰减。
RT 理论是基于粒子阐释波传播的一般性的散射理论(见第 II 章 A 节的讨论)。它通常用比强度(定义为单位面积的辐射功率)、实体角和频率来表示。比强度服从波尔兹曼微分方程,即辐射传递方程(RTE),可通过蒙特卡罗(MC)模拟求解。
有趣的是,这种模拟(MC)可以处理复杂的边界条件,如果换作是分析方法来处理这些条件, 即使并非不可能也困难重重。
RT 理论的泛用性对于衰减逆问题至关重要,因为超声波在岩石中的散射可能会导致两种极限情况之间的中间机制:弱散射机制和强散射机制,前者可以用单一散射分析模型很好地描述,后者的 RTE 与扩散方程近似等效。然而,应用 MC 模拟来描述波在有限尺寸岩石中的传播需要仔细处理边界条件和波源的几何形状。
与地震学中使用的层状半空间模型不同,实验室实验中使用的岩石样品通常为立方体、板状或圆柱体形,以便于对压力、温度、饱和度等进行实验控制。正如光学以及后来的地震学所显示的那样,要确定传输参数,必须正确考虑来自这种有限尺寸样品的边界反射。
对于板状多晶体,可以根据现有的稳态 RTE 解法来实现,但对于含时 RTE 就需要进行数值求解。对于花岗岩和辉长岩中的超声波测量,以前只考虑了相干弹性波从边界的反射。在此,我们研究了多重散射机制中边界反射的影响,以充分推断本征衰减和散射衰减(或弹性平均自由程)。
此外,超声波源传感器通常是有限尺寸源(而不是点源)。当声源相对于传播距离较大时,可以假定声源的几何形状为平面波。在这种情况下,能量曲线会明显变宽,峰值时间也会延迟。当声源小于传播距离时,可将其视为点声源。在这里,我们在 MC 模拟中精确考虑了源尺寸效应,并研究了它对反向衰减的影响。
在第 II 节中,我们回顾了标量 RTE 及其含时解析解,然后介绍了在无限介质和具有边界反射的有限尺寸介质情况下使用 MC 仿真对 RTE 的数值解析。在第 III 节中,我们研究了有限尺度源的影响。我们特别关注边界反射和源尺寸对 MC 模拟推断出的本征衰减 $Q_{i}^{-1}$ 和散射平均自由路径 $l_{s}$ 的影响。
在第四节中,我们将模拟的能量曲线与在封闭的干燥粒状介质和花岗岩(即多晶体岩石)上获得的实验数据进行比较,以解决逆向问题。
- Time reversal of ultrasound in granular media
对颗粒堆积中超声波的时间反转(TR)聚焦进行了实验研究。从压缩或剪切传感器源发射的脉冲弹性波通过 TR 镜测量、时间反转和反向传播。我们发现,弹道相干波在源位置上的 TR 非常稳健,与驱动振幅无关,但空间分辨率较低。相比之下,通过透镜效应,多重散射的尾随波可在小振幅上提供更精细的 TR 聚焦。
然而,当振幅较大时,由于振动引起的接触网络重新排列,这些 TR 聚焦信号会显著降低,从而导致时间反演对称性的破坏。我们的观察结果表明,就对扰动的敏感性而言,颗粒声学介于粒子运动和波传播之间。这些实验室测试得到了由质量和弹簧组成的无序二维渗滤网络中弹性波传播数值模拟的支持,应该有助于解决自然过程中的声源定位问题。
- Transitional nonlinear elastic behaviour in dense granular media
我们通过谐波激发的振幅测量,研究了声音在受压玻璃球堆积中的非线性传播。根据动态应变与静态应变之比 $r_{s}$ 的函数关系,我们证明了声物质相互作用的两种截然不同的状态:可逆和不可逆。
在可逆机制下,激发的高次谐波与基于 Hertz 接触理论的平均场模型非常吻合,从测量的二次谐波振幅推导出的非线性系数 $\beta$ 与声弹性测量推导出的非线性系数一致。
超过一定阈值($r_{s} > 3\text{%}$)后,声波与颗粒物质的相互作用变得不可逆,并伴随着介质的微小压实。
在致密颗粒堆积中(固体体积分数 $\phi_{S}$),“桥” 和缓慢致密流动等突出的机械特性是由不均匀的内部应力场决定的[Jaeger 等人,1996 年]。相干和多散射的小振幅声传播为表征颗粒材料的结构和粘弹性特性提供了一种高效、非侵入性的探针[Liu 和 Nagel,1993 年;Jia 等人,1999 年];然而,在高振幅波激励下,材料的非线性弹性行为变得越来越重要.
在普通弹性介质中,人们对有限振幅声传播进行了深入研究,以了解许多非线性声学效应,例如随传播距离而产生的累积波失真以及参数阵列的概念[Hamilton 和 Blackstock,1998 年]。与岩石[Guyer 等人,1997 年;Van Den Abeele 等人,2002 年]和土壤[Lu,2005 年;Gilcrist 等人,2007 年]类似,非粘性颗粒材料也表现出强烈的静态和动态非线性行为,包括强烈的声弹性效应、动态波滞后和动态模量软化[Liu 和 Nagel,1993 年;Johnson 和 Jia,2005 年]。
事实上,低约束有效压力下的接触力网络是脆弱的,在受到高振幅声传播时可能会重组[Liu 和 Nagel,1993]。然而,这些非线性行为背后的物理学原理仍不清楚,从第一原理计算中推导出的理论也无法用于此类无序介质。
最近,一种基于 Hertz 接触理论的拍击模型被提出来描述颗粒介质中的波解调[Tournat 等人,2004]。这种触点开闭的可逆机制已被广泛应用于裂隙异质材料中,但在颗粒材料中可能不太适用,因为在拍击过程中,珠子及其触点会发生不可逆的重新排列,从而松散与邻近材料的接触。
工作日志
10 月
2023.10.13
完成了声学探测装置的组装, 通过网线连接到了实验室的电脑里. 初步掌握了配套软件的使用方法. 由于最终目的是要将声学探测和 CT 探测结合起来, 所以两者的同步率也非常重要. 幸运的是, 清远公司在这个设备上做了时间戳处理, 时间同步是通过网络时钟确定的. 但是有关 CT 设备在时间戳方面的设置还不清楚(准确地说, 是对 CT 装置本身都还不清楚!), 以后组装的时候需要对这方面进行考虑.
初步拟定了一个工作计划:
熟悉使用声学探测仪器
多阅读几篇有关声学探测的文章
修改任务书和开题报告
根据现有仪器重新设计声学探测仪器, 根据师兄的指导学习颗粒制备等技能
2023.10.18
完成了任务书和开题报告的交稿, 估计后面还会继续和毕设的助教在开题报告的格式上面扯皮(很奇怪, 在 Latex 已经广泛应用的今天, 为什么不直接做一个模板, 大家直接往里面填内容就完事了呢?). 和师兄交流了一下, 下一步应该是设计和搭建实验装置, 我现在有两件事情需要做:
找到 Solidworks 资源并且安装, 找到一个教程用于熟悉和使用;
重新阅读找到的声学探测相关的资料, 初步确定装置的尺度信息, 做出初步的实验方案规划
2023.10.25
今天师兄告诉我声学功率放大器到了实验室, 我准备今天把装置取到实验室, 结合之前的超声波探测器一起测试一下装置搭建的可能性.
评估内容你自己设定,可以参考一下下面这些:
被动接收模式:实验室环境噪声的强度水平是多少分贝,人说话的声音是什么水平,颗粒物质运动的声音是什么水平,可以用采集软件自带的功能做FFT,看看频谱特征频率怎么样等等。
主动接收模式:用两个传感器相对放置,一个从信号发生器接收信号,另一个采集。可以看看输入信号分别为正弦波,方波,脉冲波等等的时候,通过空气介质或者颗粒介质接收到的信号分别是什么波形、两个传感器表面间距对于采集信号的影响、使用功率放大器与否的影响等等。
因为是试用品所以只能用到 10.31, 所以需要充分利用这段时间. 注意保存配套零件以便到时候再寄还.
和老师的讨论后的结论是先做一些简单的实验, 所以设计环切装置的事情可以先搁置. 但是, 学习 SolidWorks 使用, 设计方形或者圆筒形的颗粒容器也是需要继续的.
重新连接了 RAEM 软件, 里面有关 IP 地址的设定让人头昏脑胀, 后续会写一个专门的教程. 如果明白有关 TCP 的知识应该会好很多, 不至于像今晚这样盲人摸象一样匹配, 但是物理系的学生应当秉承 “拿来主义”, 不求甚解; 能用就行.
明年会和实验室里的师兄协商一下信号发生器的使用时间. 许家兆师兄申请的样机其实连接还算比较简单, 关键是我对于电路知之甚少, 只知道信号放大可以是 $0-20\text{dB}$, 步长为 $2\text{dB}$, 至于 $\text{Rin}$ 和 $\text{Rout}$ 应该是和信号源的内阻有关, 但是更细一点的内幕就不太清楚了.
今天的收获主要还是在自学了怎么从 0 开始配置超声探测装置, 前面师兄说的是只要会用就行, 但是今天到了实验室发现之前的配置全部都失效了, 所以也是看着说明书一步步配置完了. 还有就是实验室的电脑只有 1080P, 看起来有些糊, 趁手程度当然还是比不上自己的电脑. 也许后面会和师兄一样弄个向日葵连接.
2023.10.30
今天参与了组会, 虽然自己的实验进度不堪入目, 但是还是得到了很多建设性的意见.
我的大致思路是, 方盒中的颗粒会产生背景辐射, 并且还会产生非常明显的特征频率. 并且, 人声, 摇动颗粒等行为均不会对该特征频率产生任何影响.
但是有一个问题: 没有考虑在空气中进行裸测, 无法排除是不是实验室本身就有着这种特征频率的信号. 为了避免这种可能, 需要补测空气中的信号.
另外, 邢义师兄表示, 空气其实是超声波的不良导体, 应该考虑在水或者其它介质中进行实验.
在许家兆师兄提前看过我的展示 PPT 并且听过我的讲述之后, 给出了新的实验思路:
一、被动式:
- 不放在颗粒中测量直接环境噪声(43dB会不会有点高了,我记得上次设置40dB的门限的时候是接收不到信号的)。
- 测量搅动颗粒的声信号(即把探头放在装有盒子里和颗粒直接接触,然后用棍子搅动颗粒模拟剪切行为,观察接收到的信号变化)
二、主动式:
- 评估对信号的转换和接收:信号发生器用固有频率150Hz输入不同波形(正弦波、方波、脉冲波)的信号,两个探头直接接触相对放置(放在自带的夹具里磁吸在一起),看接收信号的波形是否和输入一致;
- 评估测量的频率范围:选定一种波形,将输入信号频率从60kHz到400kHz范围内调节,观察接收信号的变化(强度和波形);
- 评估空气的衰减:选定一种波形,将两个探头的距离从0到20cm之间等距调节,观察接收到的信号的变化(主要看强度);
- 功率放大器测试:两个探头直接接触,看功放的放大倍率和放大效果。以及使用功放与否,能探测到信号的传感器之间的极限距离的差别。给出功放是否必要使用的结论。
- 静态颗粒加压模拟测试:用一个小袋子装一些颗粒,用夹具隔着颗粒磁吸在一起模拟加压情况。可以竖直放置,这样可以在上面压金属块调节压强。可以作为预实验。参数你自己根据颗粒尺寸设置。给出声学装置测量颗粒声学是否好用的结论。
今天还在罗茹丹师姐的帮助下熟悉了 1 号楼 3 楼的 3D 打印实验室, 初步学会了颗粒的制备流程, 后续应该会写一份颗粒制备的教程. 这里先简要记录一下:
在电脑上导入颗粒的模型(这个需要提前在 SolidWorks 上面做好), 利用复制操作做好颗粒阵列, 注意在颗粒之间留出一定的间距.
维护 3d 打印机. 注意支撑材料(SUP)和打印材料(ABS)的提前更换. 瓶盖需要轻微扭松以确保气压平衡. 注意清洁陶瓷板(打印平台), 打印机本身非常容易积灰. 注意清理废料袋.
打印完成后, 放入冰箱进行冷冻, 等待成型后分别取出含有支撑材料的颗粒板, 并且在这个过程中完成陶瓷板的清洁.
将颗粒取入放到具有较大尺寸和孔径的筛网容器中, 放置在加热干燥室中, 等待支撑材料熔化流出. 等待完成后转移到具有较小尺寸和孔径的筛网容器中.
超声清洗. 可以提前烧好开水减少加热时间. 注意控制温度为 $58-62$ ℃, 原则上不应该超过 $60$ ℃, 但是温度绝不能低于 $58$ ℃.
清洗的具体过程将是明天中午的时间讲解.
2023.10.31
粗糙记录一下听到的有关清洗步骤的内容:
在将颗粒转移到大孔径大尺寸筛网上并放置于烘烤箱中时, 可以在此时一并清洗陶瓷板. 此时可以使用无水乙醇将陶瓷板上的所有有机材料一并洗去.
提前用热水壶烧开水, 配合冷水混合配置出 $58-62$ ℃ 的水温.
第一次和第二次的清洗需要加入洗洁精, 用量约为 $5\text{ml}$, 计算在按压上约为 $15-18$ 次. 倒入时可能会有部分液体粘于容器壁, 可以使用超声波清洗机里的热水荡洗溶入.
注意干燥箱里的熔化出的支撑材料需要及时清理, 避免其溢出烘烤箱.
超声清洗装置加热的设定温度为 $64$ ℃, 但是实际操作过程中应当配合使用酒精温度计.
倒入提前配好的热水, 注意水线约为筛网容器容深减去约 $3\text{cm}$. 戴好手套, 用手将取自干燥箱的颗粒尽快放入已经盛好水的筛网中, 开启超声进行清洗.
一般设定的一轮清洗需要进行约 $10$ 次玻璃棒搅拌. 可以配合记录笔记提醒自己完成完整次数的操作.
如果清洗过程中水的温度下降较快, 可以将盖合上. 在这个过程中可以继续使用热水壶烧制开水, 以备下一轮的清洗使用. 一般是 $2-3$ 壶热水倒入热水桶中并且倒入冷水中和, 过程中可以使用酒精温度计测量温度.
等待 $30$ 分钟后, 一轮清洗完成, 开闸放水, 将洗涤残余支撑材料的废水导入红色水桶中. 注意此时的温度仍然比较高, 可以选择将其放置变凉倒入洗手池或者开冷水倒入.
注意放水过程中, 需要注意不要让颗粒露出液面接触空气(具体原因未知), 接近露出时闭闸, 然后按照上述的洗洁精加入等步骤进行第二轮清洗.
等待下午进行后续清洗步骤的讲解.
下午因为临时调度没有办法帮上清洗颗粒的忙
托赵西梅老师借了 3 号楼的声学装置:
信号发生器 * 1, 示波器 * 1, 声速测量仪器(两个压电陶瓷做的换能器, 上面有刻度尺) * 1, T 型 BNC 接口, BNC 线材 * 4(接口上三根外加额外的一根)
算是重温了一下本科物理实验, 声速测量有
- 共振法
共振频率可以通过调节发射频率, 观察接收到的信号是否出现极大值, 然后按照此法依次调节发射信号的十位, 个位等数位的具体数值, 由此确定发射频率 $f$.
因为两个压电陶瓷实际上是等同的, 所以接收端的探测器在接收到发射过来的信号时也会反射信号至发射端, 当两者间距为半波长的整数倍时就会形成共振响应, 体现在接收端上就是形成信号峰的极大值.
所以记录下峰为极大值的位置, 使用逐差法就可以确认(半)波长 $\lambda$.
根据以上数据就可以得到声速的测量值 $v = f \lambda$.
- 相位法
将输入信号作为 X 轴, 接受信号作为 Y 轴, 在示波器上就会出现各种李萨如图形. 形成一三象限的直线即为同相, 二四象限的直线即为反相. 记录出现(反)直线的位置, 使用逐差法计算得到(半)波长 $\lambda$. 计算出声速的方法与上述公式相同.
- 时差法
我猜测论文里经常提到的 Time of Flight (TOF) 就是这个方法. 之前还在使用 RAEM1 的时候我就在考虑怎么确定发射时间, 现在有了一个 T 头的 BNC 接线就了然了.
要测定声速还是要用其良导体才好, 这里在导师千叮咛万嘱咐之后在实验桌上加了水. 设定一个合适频率的脉冲波, 当然还要注意设定示波器合适的 Scale, 要让发射的脉冲信号(比如黄色信号)和接受信号(比如紫色/粉色信号)同屏出现, 使用 Cursor 就可以轻松计算出两者的时间差(一般几十到一百多微秒).
这里还要注意的是, 这样的时间差 $\Delta t_{i}$ 和探头距离 $L_{i}$ 不能直接相除, 因为还需要考虑声电/电声效应的固有时间, 所以正确的做法是拟合两者出现的直线, 然后将其斜率作为采用值.
$$ L = \color{red}{v}\times (\Delta t - t_{0}) $$
11 月
2023.11.1
昨天晚上的实验相当于是用空气和水做了一次练手, 现在需要考虑的是:
- 如果是在颗粒物质中会怎样?
从这里就需要涉及弹性力学相关的知识了. 加上前面的在学 Edwards 统计方法, 我觉得我也应该安排时间来学习一下热力学的知识了, 虽然书是已经买了放到了工位, 但是除了预录取面试前夕的抱佛脚, 目前因为杂七杂八的事情都还没有好好学过.
如果要真正研究应力等因素对有效介质的影响, 没有系统学过弹性介质肯定是不行的.
另外, 原本用作空气和水的容器比较大, 用于颗粒物质的话, $5\text{mm}$ 所需要的数量会很大, 肯定不是借用许家兆师兄的备用颗粒能够做到的, 怎么借调到这么多的颗粒也是一个问题.
- 如何将 RAEM1 的这一套装置实现出声学仪器类似的效果?
广州的这个声学装置的主要优点可能也就在可以方便地做一个 FFT 进行频率分析, 但是说实话可能没有什么大用. 比如前面提到的 TOF, 如何实现在 RAEM1 上还是一个悬而未决的问题.
另外, 尚不清楚 RAEM1 和示波器之间的适配性, 理论上来说只是将声学装置中的压电陶瓷探头换为了 RAEM1 的探头, 但是能否实现, 如何实现等问题都亟待解决.
2023.11.03
今天稍微整理了一下这一周以来的实验情况, 也和导师交流了一下, 发现了之前做实验没有考虑到的一些问题. 现在趁着还有记忆在这里陈列一下:
$\sqrt{}$ 凡是都要考虑空白对照, 比如之前摇晃颗粒的时候确实记录了对应过程的信号, 但是没有考虑到 无任何处理 的颗粒介质中的信号, 所以这个实验回头需要补测.
$\sqrt{}$ 不要太过依赖软件的计算功能(比如 FFT), 尽可能自己写好脚本来处理数据.
$\sqrt{}$ 和技术再次确认如何稳定使用连续采集而非包络采集;
? 为什么 RAEM1 和示波器上观察到的图像不一样. e.g. 正弦波和带有锯齿的正弦波?
? 为什么 RAEM1 上没有观察到对应的倍频效应?
$\sqrt{}$ 确认单位 dB 的计算方式, 由此确定信号之间的差异倍数是如何得到的.
$\sqrt{}$ G150 探头的含义是共振频率为 $150\text{ kHz}$, 但是为什么实验测得的共振频率为 $129.2\text{ kHz}$? 是不是漏测数据了?
$\sqrt{}$ 和技术再次确认探头的信号发射的方向性的问题, 理论上超声信号在空气中的传播应当方向性很好.
$\sqrt{}$ 没有考虑到信号发生器的共振频率的问题, 找相关人员或者资料确认对此频率数值是否有研究的必要, 或者还是说可以忽略这个问题.
$\sqrt{}$ 用相对粗糙的压强施加方法来制备一个致密堆积然后测量, 至少要先观察到和 Jia 论文里相似的波形, 即一个相对快, 幅值大的相干弹道波和一条相对慢, 幅值小, 广谱的散射波.
接下来的一段时间应该是处理开题答辩的事情. 我已经受够繁文缛节了.jpg
2023.11.06
完成了开题答辩, 因为太经典力学(不涉及任何量子效应), 太实验(不涉及任何模拟计算), 答辩专家们反而无计可施了, 除了郑杭老师问了问实验室的配置, 没有其他问题可问.
9 月的时候和导师面谈, 说是 “比较独立的方向”, 现在我信了.
完成了这些形式主义的东西之后应该就是继续回到实验, 准备把上面的几个问题一一解决. 另外今天下单了网口拓展坞, 明天就能到货, 希望可以顺利迁移程序到新电脑上.
- dB 的定义方式
首先需要明确的是 以 $10$ 为底, 并且是功率相比.
因此我们也就可以理解为
$$ N_{\text{dB}} = 10\lg{\frac{p_{i}}{p_{o}}} $$
所以功率放大器增益 $x\text{dB}$ 就是指的
$$ N_{\text{dB}} = 10\lg{\frac{U_{i}^{2}/R_{i}}{U_{o}^{2}/R_{o}}} $$
- Matlab 实现 FFT
目前已知 Origin Pro 也具有非常方便的 FFT 功能. 但是为了方便地进行数据分析, 最后还是要落实到自己写代码上.
另外确认了一下, RAEM1 的采样频率应当是 $2\text{ MHz}$, 也就是 $2000\text{ kHz}$. 而借来的示波器的采样频率是 $1\text{ GSa/s}=1\text{ GHz}$. 这意味着, 我们的探测设备很有可能难以满足后续的实验需求.
但是我查阅了一下 Stick-Slip 的文章, 里面的信号采样频率也就是 $2\text{ MHz}$, 明天应该再去找导师去确认一下.
clear;clc;
%%% This code was created to read the dB.csv created by
%%% RAEM1.
%%% 1. Read the data in the *.csv file
data = readmatrix("dB.csv");
[Length, Width] = size(data);
Amp = data(4:Length, 1);
num = Length - 3;
Freq = num / 5 * 10^3;
delta_t = 1/Freq;
tspan = (0:num - 1) / Freq;
fspan = (0:num - 1) * (Freq / num);
%%% 2. Draw the time-domain signal
figure(1)
subplot(2,1,1)
plot(tspan*10^3,Amp)
xlabel("Time(ms)")
ylabel("Amplitude(V)")
subplot(2,1,2)
ref_Vol = 1e-5;
%%% RAEM1 的分贝值是如何计算出来的?
Amp_dB = 20 * log10(abs(Amp)/ref_Vol);
plot(tspan*10^3,Amp_dB)
xlabel("Time(ms)")
ylabel("Amplitude(dB)")
%%% 3. FFT.
%%% Remember that the sampling rate is 2 MHz, so the time step
%%% equals to 1 us.
DFT = abs(fft(Amp));
half_num = floor(num / 2);
figure(2)
plot(fspan(1:half_num)/10^3, DFT(1:half_num))
xlabel("Frequency(kHz)");
ylabel("Amp");
- 信号发生器的共振频率
如果探头的共振频率和信号发生器的压电陶瓷共振频率不同, 确实可能会影响到实验结果. 但是信号发生器是否具有这样一个特质: 当我们选择到一个频率 $f_{0}$ (比如 $129.2\text{ kHz}$)的时候发射, 信号发生器会将自己的共振频率选定为 $f_{0}$?
还有一个问题, 信号发生器本身到底有没有所谓的一个压电陶瓷存在? 我怀疑其本身只是调制了电流而并没有一个真正的压电陶瓷.
查阅了一下, 并不是所有的信号发生器都是使用的压电陶瓷作为振荡器, 这取决于具体的设计和需求. 明天应该看看这个信号发生器的型号(顺便也把实验室里其余的信号发生器信号也记一下), 看下都各自是什么工作原理, 再做进一步打算.
压电控制器 & 信号发生器.
- 超声辐射的方向性
超声波甚至可以用来测速. 这是不是说明, 这个 G150 探头产生的信号强度其实并不太高? 否则为什么只是隔了几厘米, 信号强度就衰减到和背景噪音强度差不多的程度了.
超声波的频率越高, 方向性会越尖锐, 但随之而来的是衰减也越大.
2023.11.07
今天不仅完成了软件的迁移, 还学会了如何操纵 RAEM1 的连续采集方式. 而且, 许家兆师兄带来的金属片很好地充当了临时活塞头的效果, 把各种金属(师兄们加工过的金属块, 还有一大袋的金属球珠), 形成的致密颗粒堆积的传声效果确实比之前的松散堆积好多了.
今天通过一些简单的实验也发现了不少问题, 现在趁着记忆还在简单梳理一下:
- 连续采集虽然声称是 0 间隔进行区间采集, 但是细看 “全波形” 图像会发现实际上还是有空隙的. 如何确保所需的数据完整的被采集到一个区间内将是一个需要研究的问题.
- 关于设置信号频率的问题. 首先需要明白: 为什么要测共振频率? 在测水的声速进行练手的时候, 需要注意到我们实际上并不是使用的水中的共振频率, 而是简单的设置了 $100\text{ kHz}$, 然后观察接收信号出现的位置和时间.
实验装置的需求整理:
-
能够方便地安装和卸下 G150 探头, 并且能够通过滑尺等方式测量探头之间的距离.
-
能够方便地控制施加应力, 目前的容器施加压强的方式比较定性, 无法精确控制.
还有关于 RAEM1 和示波器之间的协调关系. 示波器是不是本身在外部有 BNC 线材接入的情况下就会出现一个误导性的电压抬升和波动?
具体来说, 就是把频率调为 $100\text{ Hz}$ 的时候, 就可以看到类正弦的接收信号在 $t = 0$ 处会有一个相对高峰, 当时还以为真的测到信号了. 然而, 无论是将信号发生器的输出关掉, 还是干脆直接把信号发生器上面的 BNC 接口直接拔下, 这个疑似相干弹道波反而还更清晰了(在没有任何信号被激发的情况下, 接收端竟然接收到了信号!)这无疑是非常荒谬的.
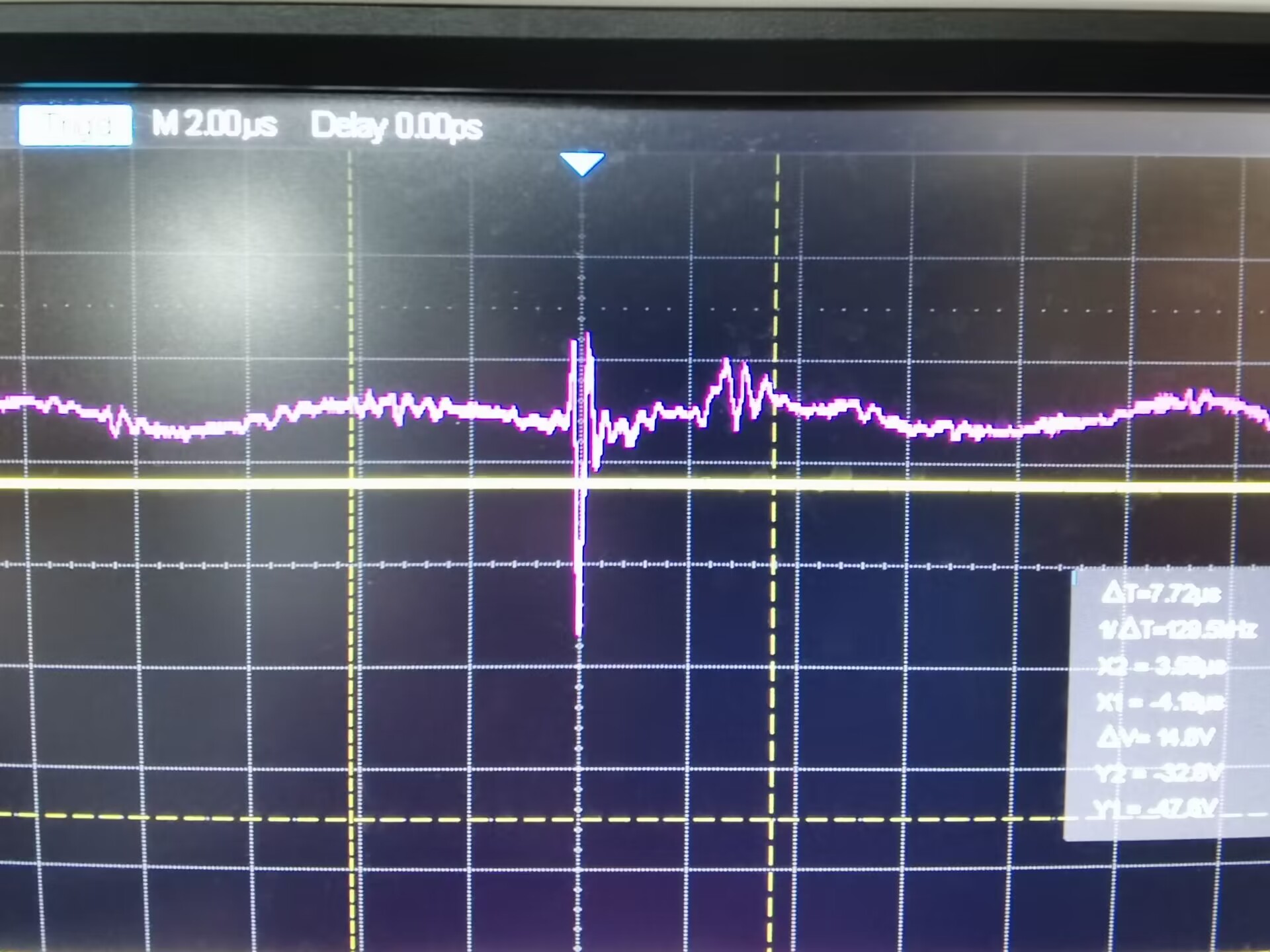
因为在参考的论文中设定的脉冲是 $2\mu\text{s}$, 我理解的是这个数值就是指的脉冲的宽度(Width), 所以频率就在 $10-1000\text{Hz}$ 里面选择, 这种思路和测水中声速是一脉相承的. 并且, 确实可以在紫色信号看到有意义的峰, 而非散乱的信号杂音. 但是, 并没有看到所谓的相干弹道波, 这一点对于我们的散射理论反而是更重要的.
目前的话, 我认为应该重读一下当时参考的声学探测论文, 还有就是以周志刚的这篇博士论文为纲学习颗粒物质. 之前给的夏成杰师兄的文章固然好, 可惜并不是从声学角度给出的, 如果我要从声学入手颗粒物质检测, 那么跟着周的文章学自然是最轻松的.
昨天的开题报告, 实际上已经是部分同学的结题报告, 不由得感叹人生的参差. 悟已往之不谏, 知来者之可追, 在这一年抓紧时间熟悉课题组的工作内容, 更应该是现在应该去上心的事情.
11.13
记录一下周四和导师交流产生的悬而未决的问题.
如何解决 RAEM1 只有单通道的问题. (涉及测量时间差从而测定声速的问题)
实验室的装置, 应当先斩后奏, 买了再报销; 不能一直被动地等.
重新调研信号和颗粒的参数, 需要将对应的参数匹配到自己的装置中.
如何观察到相干弹道波的现象.
目前我的研究进展的痛点:
- 急需一个能够满足自己研究需求的装置, 这个装置需要:
- 回顾 Jia 和 Zhou 的论文, 总结他们的装置参数和对应的实验图像, 从而做出自己的实验装置设计和图像预期;
- 使用 SolidWorks 进行设计;
- 声学和通用的颗粒知识学习应当齐头并进, 不可偏废.
记录一下新的装置到了之后产生的效果:
- 信号发生器能够产生 N-Cycle 的信号, 基本上可以用于复现 Jia 的脉冲信号;
- 示波器比起之前借用的示波器更高档一些, 但是仍然是噪音波动还会有残留效应, 导致在观察波形(包含波前起点)的时候比较困难, 需要用到信号放大器把发生器的信号再次放大在可以看到比较明显的现象.
不难观察到, 随着循环数的增加, 接收信号得到的幅值也会更高. 但是, 我们不能无限制地增加循环数, 因为这样就会导致信号的重合. Jia 文章设定为 $10$, 但是在实际的操作过程中, 可以将循环数设定到 $15$ 左右.
通过示波器的 Cursor 获取时间差(~ $200\text{ us}$), 再通过刻度尺测量两个探头之间的距离(~ $5\text{ cm}$), 最后计算出的声速约为 $200-300\text{ m/s}$, 和 Zhou 论文里的数量级大致相仿, 具体的差异可能还要看颗粒参数和边界条件.
我的想法是, RAEM1 的单通道性能其实比较废物, 我目前也没有想到什么除了再买一个 RAEM1 然后接入到 SWAE 以外的方法. 显然这是很浪费的; 并且我有理由认为, 既然 RAEM1 的采集性能也就是 $2\text{ MHz}$, 那么 SWAE 的数据处理性能上限可能也就是在这个数量级(因为从单次采集, 即 $5\text{ ms}$, 得到的数据数量刚好就是根据 $2\text{MHz}$ 来的), 所以我认为另一条路径就是, 设法将示波器和主机连接, 直接输出其波形数据. 但是这样肯定就比不上 SWAE 处理数据的方便程度了(主要是即时性, 虽然一些数据功能可以通过自己编写 Matlab 来实现, 但是终究是比较麻烦的)
另外, 目前是已经可以得到波在颗粒介质里的频谱展宽现象, 但是还没有掌握具体的分析方法(因为需要具体情况具体分析, 不能直接引用 Jia 的结论), 所以最后还是要落回到细读原文的研究方法上.
今天准备复现之前的 10 循环发生信号, 结果发现这个信号发生器比想象的要难用很多, 一直都很难调出和之前一样的效果. 导师这边又在催进度, 好像都默认周末就是用来加班加点做实验的. 虽然说的确在声学实验上投入了不少钱(新的发生器, 示波器还有专门的电脑), 但是这些都是工作上的投入, 和计算组的同学相比我觉得我都算是勤奋的了. 新的装置又不可能一夜之间就做出来了, 前面的技术和知识铺垫哪一个都是需要花费时间的. 现在如果要说尽快有进展, 那就只能换颗粒材料, 看下玻璃珠和钢珠都是什么情形, 但是这个本质上是没有在技术上获得新进步的, 所有的测量操作都是一样的. 总结下来就是一句话: 欲速则不达.
11.14
今天又额外举行了一次组会, 虽然说是定的下午两点半, 但是实际上还是延误了十来分钟才开始的. 今天开的组会也是重量级, 一次开了接近五个小时. 下了楼四餐早关门了, 就去全家买了个三明治, 感觉还不错.
先简单记录一下今天参与组会的感受.
要避免像王鑫师兄那样, 一次性考虑太多的因素. 比如, 在做粮仓效应的时候考虑尺度, 摩擦等众多因素. 导师的意见是: 我们设计实验是为了解决问题而不是提出更多的问题, 要成为实验学者而非理论学者.
积极参与到组会中的思维训练中, 导师随时都有可能抽奖到你来回答一个科研思路问题. 这就要求听组会的过程中要精神集中, 清楚各个师兄师姐都在干什么.
再简单说一下今天做的实验. 今天主要是考虑了循环数对于响应信号的影响, 目前结果是已经出来了, 但是如何对结果进行分析, 仍然不得要领. 另外, 速度时已经可以测出来了, 应该是比 ABS 的塑料小球要快一些.
昨天做了一个小的固定时间测试实验, 即把两个探头使用夹具相吸固定测时差, 结果显示的确存在约有 $1\mu\text{s}$ 的时间差, 而测速度的时候的时间差也是~ $200\mu\text{s}$, 虽然说相比之下确实小很多, 但是将其考虑进去也会更加科学.
缺少信号放大器带来的效果也很快显现了, 虽然信号发生器已经尽可能调到最大幅值(10 Vpp), 但是反应在接收信号上, 对比度就显得有点小了.
下一步的打算是:
-
想办法初步控制压强(应力);
-
学会使用信号发生器的任意波形功能, 模仿判断飞行时间选取的小实验.
11.15
论文重读和问题研究:
- Sound pulse broadening in stressed granular media
为了获得相干压缩波在颗粒介质中的脉冲响应,我们可以用源传感器发送的信号 S 对通过介质传输的信号进行解卷积(deconvolve). 这里的解卷积的原理和用途是什么?
该文章中的发射信号并不是之前设定的方波脉冲, 而是自己设定的波形.
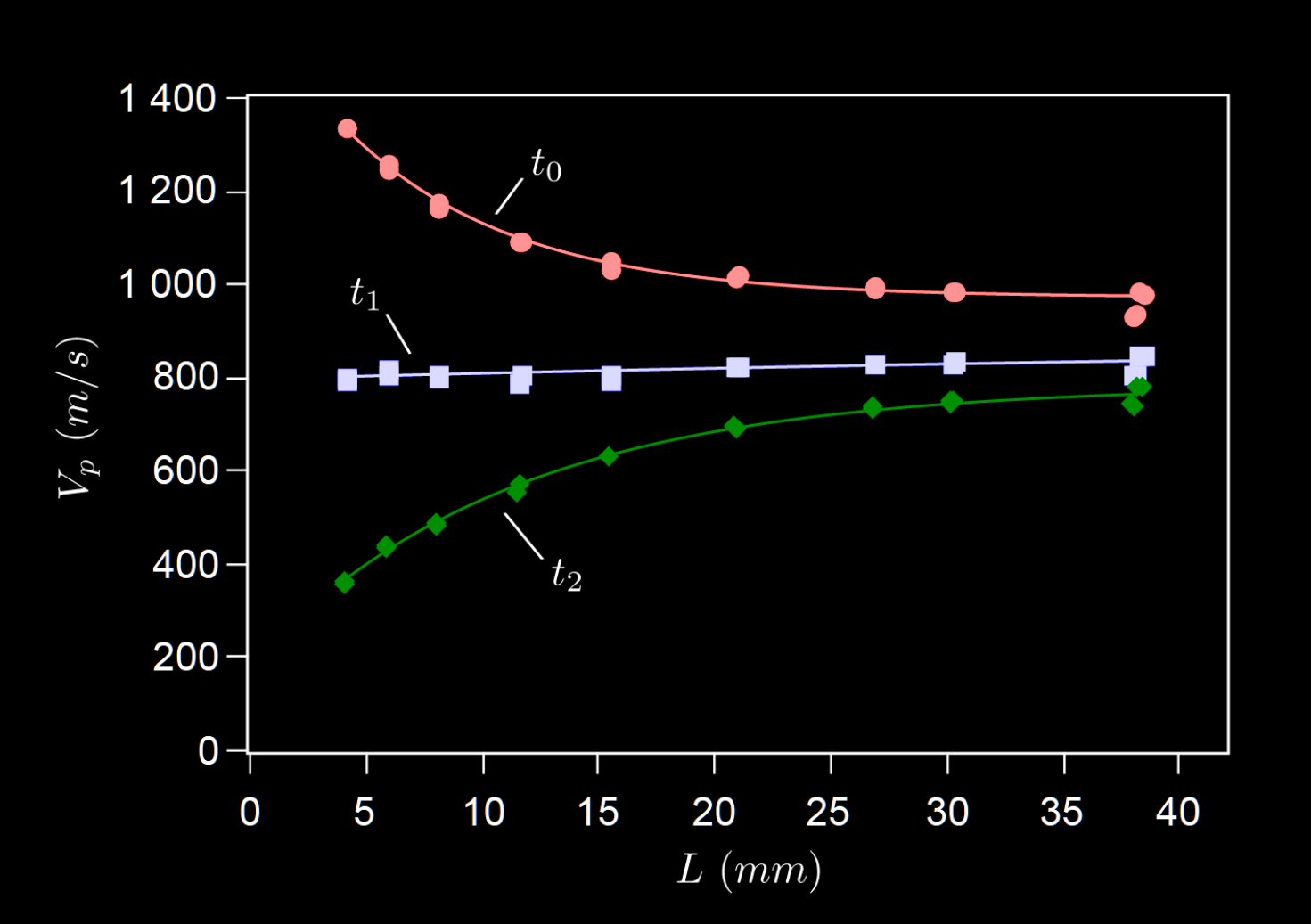
飞行时间的定义方法涉及参考点的选取: 峰值*10%($t_{0}$), 峰值($t_{1}$), 首次过零($t_{2}$).
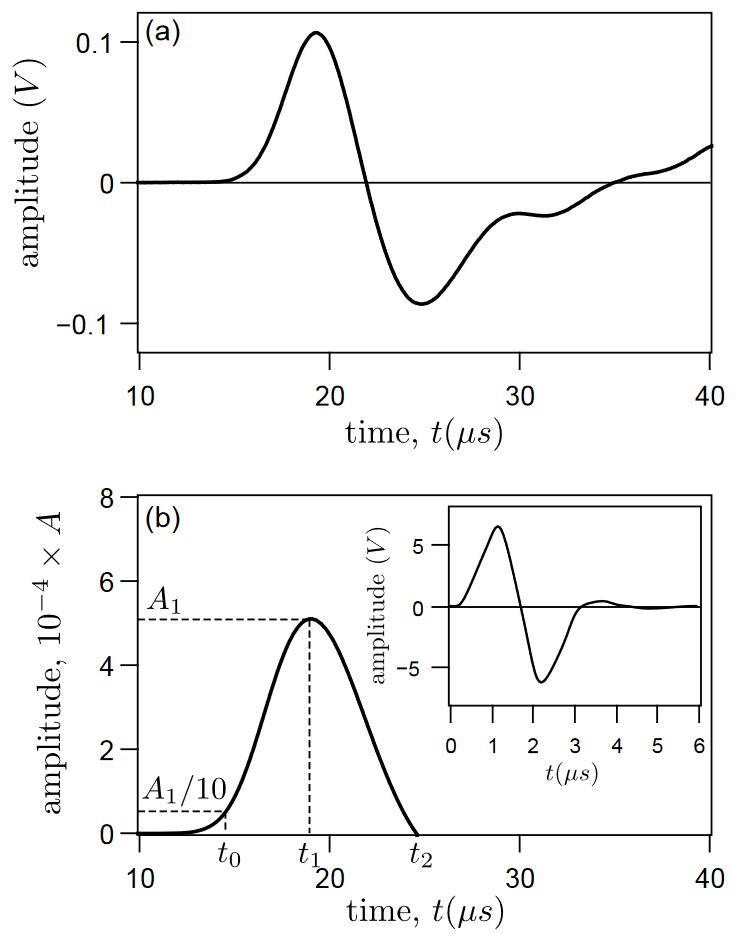
参考信号是在参考介质中测定的. 实验发现, 用 $t_{1}$ 测得的速度几乎与探头间距无关. 在正式实验中, 显然这也是一个值得探究的点, 可以稍微做一点数据出来说明选取的合理性.
可以通过重标定(rescale)检查响应信号, 即 $A/A_{1}, t/t_{1}$.
还有极其复杂的一维展宽推导和数值模拟
- Ultrasound Propagation in Externally Stressed Granular Media
目前已经能够掌握粗糙的飞行时间速度测量, 如何从简单的波形上确定群速度? 如何统一两者在颗粒介质中的描述思想?
除了飞行时间速度以外, 还有周志刚提到的反射声波法, 多普勒效应法, 共振柱法, 后面应当再独自调研一下, 了解为主
颗粒的尺寸将会显著影响相干波的形状. 可见, 在颗粒尺度较大的情况下信号被严重散射了, 应当考虑使用尺寸更小的颗粒, 这样观察到的相干波应当会产生一个对比度极高的峰.
注意要区分两种相干波, $E$ 波和 $R$ 波. 后者是前者的反射波.
信号参数: $500\text{kHz}$ 为中心的宽带频谱($20-1000\text{ kHz}$), 持续时间 $2\text{ ms}$, 振子振幅为 $10\text{ nm}$(需要用干涉仪才能够测定).
颗粒参数: 都是多分散, 分为三组: $0.2-0.3, 0.4-0.8, 1.5\pm 0.15\text{ mm}$
飞行时间确定是首次达到峰值的 $5$%. 有效介质速度为 $v_{\text{eff}} = 1070\pm 30\text{m/s}$.
注意: 探测器尺寸也会影响到信号, 减小尺寸会增强散射波(S)的振幅. S 对构型高度敏感而 E 则复现程度高, 用 $\Delta P/P=(P’-P)/P$ 来评估这一参数. 这说明 E 是一个自平均信号. E 信号才是定义声速的信号.
声学共振频率的确定: $\nu\approx v_{\text{eff}}/d$.
- Codalike Multiple Scattering of Elastic Waves in Dense Granular Media
需要关心力链关联长度和颗粒介质中的波长之间的关系. 波长减小到晶粒大小的时候, 力链产生的散射效应将会非常显著.
信号参数: $20\mu\text{s}$, 10-Cycle, 中心频率 $500\text{ kHz}$.
颗粒参数: $kd = \omega d/v\approx 2.9, v = 750\text{ m/s}$. 应力 $P = 750\text{ kPa}$, 厚度为 $L = 11.4\text{ mm}$. 直径 $d = 0.6-0.8\text{ mm}$.
容器参数: 直径 $D = 30\text{ mm}$, 高度为 $7-15\text{ mm}$.
$E_{p}$ 幅值较小.
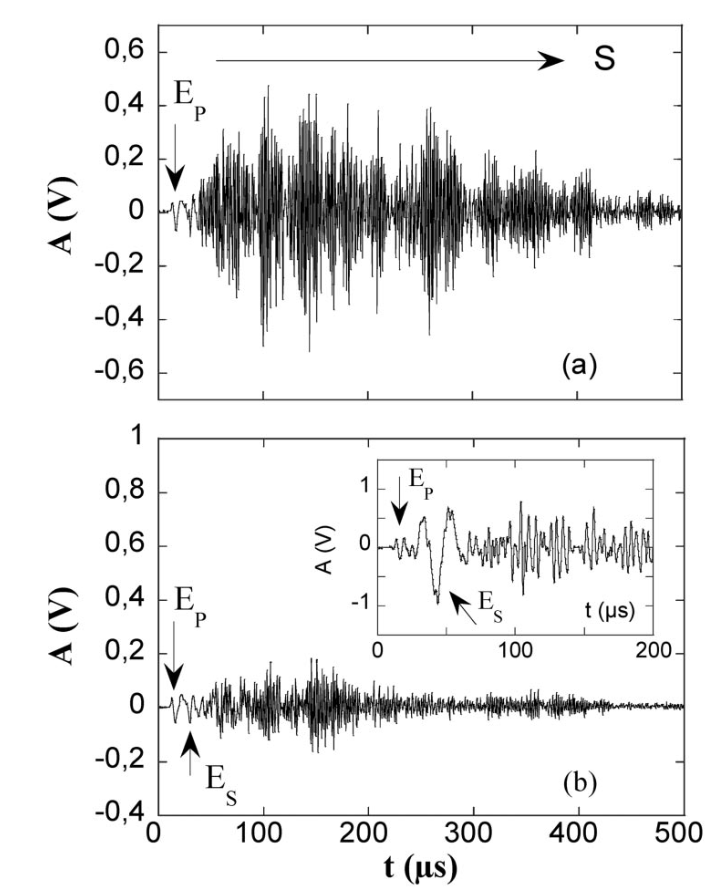
需要考虑: 如何做到的去除噪声? 如何做到系综平均?
传输的时域信号是相干分量(低频)+剧烈散射的非相干分量(高频), 能够在最新的示波器上观察到吗?
注意: 相干波存在两种, 一种是压缩波($E_{P}$), 一种是剪切波($E_{S}$), 只有 $E_{p}$ 才是自平均的, 所以它对构型不敏感; 后者使用大尺度探头更容易探测到.
为了对散射波进行研究, 可以通过数字滤波去除低频的相干波.
如何测定ABS球和钢珠的共振频率?
- Ultrasound propagation in disordered granular media
相干弹道波表现的是有效介质特征, 杂乱的散射波表现的是介质不均匀力场.
颗粒参数: $400\mu\text{m}-5\text{ mm}$. 实例数据为 $0.4-0.8\text{ mm}$.
容器参数: $30\text{ mm}$,
信号参数: 以 $500\text{ kHz}$ 为中心的一个或多个周期的输入脉冲. 持续时间为 $2\mu\text{s}$ 的单周期脉冲波, 传播距离约为 $L = 11\text{ mm}$.
表现出明显的相干弹道波特征. 随着颗粒尺度增大, E 和 S 都表现出低频特性.
$\lambda = v_{\text{eff}}/f_{c}$ 与颗粒尺度 $d$ 相当时, 将出现频率截断现象(低通特性).
如何研究多重散射声波的传输特性? 使用 10-Cycle 脉冲, $f = 500\text{ kHz}$.
11.16
今天听了邢义师兄的博士学位预答辩, 足足有三个小时之长. 可见如果没有充分的理解和研究, 面对老师的质询答不出来的话, 场面将会极其尴尬. 所以功夫在平时, 做好每一步的调研和思考, 想常人之难想, 方能天衣无缝, 滴水不漏.
在听的过程中也记录了一下问题, 目前尚不能理解:
Edwards 系综解释中, 我的理解是态数目为体积固定为 $V$ 时可能的构型数目, 这个计数应当是不涉及具体的外部驱动过程的, 为什么说需要将循环剪切和振动两种驱动类型分开看待?
如何考虑微重力下, 外部施加等重力压强, 这个可以等价于普通重力场下的颗粒体系吗? 我认为是不可以的, 因为需要考虑粮仓效应或者说 Jassen Effect, 按照反作用力去理解, 均匀外加压强显然不是同一回事.
另外在发呆过程中也思考了几个问题:
如何去除空气中的超声杂声? 为什么会存在这样的信号? 这些莫名其妙的峰可以通过使用简单的挡板来去除吗? 还是说需要用上数字滤波器?
为什么自己的 FFT 算法得出的结果和 SWAE 算出来的结果差这么多? ($\text{Amp%}$)
根据简单的波方程知识, 可以知道波速, 频率, 波长之间存在关系:
$$ \lambda = v/f $$
前面可以粗测得到等效声速 $v_{\text{eff}} \approx 220\text{ m/s}$, 所以如果是声波被剧烈散射, 就应当取颗粒直径 $d = 5\text{ mm}$ 作为波长, 计算得到的频率就是 $44\text{ kHz}$; 如果要观察到明显的相干弹道波, 就应该让频率再降低, 使得长波极限被采用, 也就是~ $4.4\text{ kHz}$.
问题在于, 感觉测定的声速有点偏小, 不知道是不是就是这么多. 可以回去再测测钢珠的, 感觉数量级都差不多.
首先是, 有关于飞行时间参考点选取的问题, 还需要设计实验来验证; 其次, 虽然 Jia 声称参考信号就是用的 “中心频率为 $500\text{kHz}$”, 但是并不清楚这个是怎么做到的, 反而是那个参考点选取的实验, 虽然波形看上去有点奇怪, 但是至少是可预计的未来时间内可以自己设计波形, 然后使用任意波形发生器激发做到的.
另外, 虽然 Jia 设定的信号幅值很小($100\text{ mV}$), 但是传播距离也很小($11\text{ mm}$). 我想, 目前涉及的不只是颗粒材质的问题, 更应该考虑频率和颗粒尺度之间的匹配关系. 目前颗粒尺度还有待考量, 但是频率尚且是可以自己控制的, 可以先做一点实验对比一下.
11.20
今天进行了一次巨长无比的组会, 虽然今天没有抽问环节, 但是仍然感觉身心俱疲(14:40-18:30, 19:30-23:00, 接近七个半小时), 主要还是最后的哲学分享环节十分折磨, 但愿下次没有这种事情发生了.
说回正事, 今天主要是讲了一下之前的 PPT 的总结, 导师没有给出什么新的建议, 主要还是要和贾小平老师及时联系, 沟通一下装置可能存在的问题. 另外就是要把三篇文件看了, 一方面是再次熟悉一下大课题的方法处理, 另一方面就是学习一下 Jia 的实验处理方法.
11.21
今天解决了一个工程学上的难点, 即在颗粒层数较多或者颗粒直径较小的情况下, 很难在已经倒入颗粒之后重新把探头埋进去. 现在想起来可以用双面胶将其固定在容器壁, 这样就可以很轻松的重复制备颗粒堆积而无需考虑探头位置的变化. 唯一需要考虑的可能就是多出来的双面胶也会固定一些颗粒从而造成浪费.
今天在没有改变容器构型的情况下, 多用了两种颗粒堆积, 但是仍然没有观察到明显的弹道波. 难道是对 $\lambda$ 的计算有误解吗?
现在重新整理一下实验做下来仍然没有搞清楚的点:
-
经常提到的 “以 $500\text{kHz}$ 为中心的宽带频谱” 到底是怎么实现的?
-
外部施加压强的影响应该需要超过重力带来的影响才可以. 但是实际上, 即使没有加上外加重物, 也足以观察到现象. 需要设计新的容器;
-
施加压强实际上会极高(~$\text{MPa}$), 所以面积就不能太大, 所以设想的容器不能够把接线长度引入, 而是必须要挖孔;
-
等效波长 $\lambda_{\text{eff}} = v_{\text{eff}}/\nu$ 里面的 $\nu$ 到底是指的什么?
-
颗粒尺度已经来到了 $2\text{ mm}$, 再尝试把距离减小试试看?
-
新的容器制作必须提上日程.
11.27
上周五的时候老师没有把关键问题问出来, 今天组会的时候才问了几个没答上来的问题. 我也发现了之前实验中存在的一些思路上的问题.
-
声学探测的原理是什么? 我们关心什么物理量的演化?
-
Jia 为什么要选定一个 $500\text{kHz}$ 为中心频率? 它和颗粒的直径有着怎样的联系?
-
不要把目光局限在静态堆积上. 尝试回答声学能够解决什么问题(关心波形, 能量)? Jia 的声学方法是什么, 解决了什么问题?
更多的信息可能需要明天看完贾老师的五小时演讲才会知道怎么做.
让我不满的是, 我本身就是以复现论文结果为主的, 让我突然成为一个声学专家是怎么回事? 还说所谓考试和他无关, 那我怎么应对明年的一系列 GPA 课程还有博资考呢?
感觉有点不太现实, 突然把一个完全很大的领域交给我一个人, 一周的时间来精通, 搞笑呢
12 月
12.05
昨天简单的介绍一下自己对于贾老师研究的理解情况, 但是邢义师兄对于我的未来学习安排有些担心. 仔细想想自己对于未来比较宏观的学习安排还是有些不太清晰, 昨天说的测定响应函数也只不过是和老师交流之后产生的新想法, 但是我对于接下来应该怎么做, 具体去做些什么, 其实并没有真正的想法.
在这里简单列举一下应该做的事情:
$\sqrt{}$ 熟悉探头的响应情况, 规划响应函数的测定方案;
$\sqrt{}$ 学习 声学原理 的声强计原理, 以及非线性声学的处理思路;
$\sqrt{}$ 自己写一个滤波函数出来, 学会如何使用 high pass 和 low pass 函数, 关于频率的截断是如何做到的.
继续学习 SolidWorks 操作, 制作一个简单的圆筒壁容器, 方便直接使用贾老师用的扩散函数.
系统学习声学的扩散理论, 清楚这个方程背后的具体原理;
继续学习贾老师的暑校演讲, 争取这周把后面的 $2/3$ 看了;
$\sqrt{}$ 地震学笔记, 继续阅读学习;
$\sqrt{}$ 问技术探头的制造原理; 学习压电效应, 搞清楚是否在线性区域内进行工作.
另外吐槽一句, 昨天收到了这样一份邮件:
你好。
由于你在报考24级直博生预录取阶段,填写的意向导师王宇杰老师,近期即将离职交大,所以你2024年9月入学后,需要更换一名意向导师,并根据学院政策,在你的第一学年结束时,再确定正式导师。
特此通知,收到本邮件还请回复一下,以便我确认你已知晓上述信息。
如有疑问,请随时与我联系,谢谢。
合着就我一个人不知道老师都要离职了. 在实验室呆了两个月, 直接人都没了可还行. 总之后面少不了多的麻烦.
今天花了不少时间在个人网页的重新整理上, 实验上的安排估计不多, 所以还是放在阅读和学习上. 明天起个早班来把实验做一下.
12.06
今天花了不少时间在声强计原理和非线性声学上, 估计这一周就可以学完. 今天看累了, 用剩余的时间写了一个滤波函数, 检验了一下还不错. 看到频域上有个 $130\text{ kHz}$ 的峰就感觉火大, 明天可以做一点粗糙而对实验检验一下自己的一些想法.
顺便今天收到了新的回信:
你好。
经请示主管领导,你的疑问答复如下:
1、王老师调离交大,等你的第一学年结束时需要正式确定导师的时候,王老师不会在导师库里,你只能在导师库里选择导师。至于你博士工作是不是还是和王老师继续合作,由你选择的导师和王老师之间确定。
2、第一学年结束时,选择的导师就是你的正式导师,该导师需要符合所有的关于导师招生人数的限额要求。
3、如(1)所述,王老师调离交大,选择正式导师时候,你无法选择王老师作为系统里面的正式导师。
特此回复,望知晓,谢谢。
总之就是很麻, 不知道去找谁, 问题就在于这个傻逼学校只能让你选有名额的导师, 那当时预推免的时候又拿出一个名额, 有点搞笑了. 为什么要让学生来承担后果呢?
12.11
今天测定了脉冲波和白噪声下的响应效率函数, 果然效果很差. 但是客观来说, 这是探头的工作范围本来就在 $60-400\text{ kHz}$ 所致.
下一步的学习安排:
- 学习贾老师暑校 (2/3), 学习剪切带如何用声波探测;
- 自己写一个 Correlation 函数判定;
$$ R(i,j) = \frac{C_{i,j}}{\sqrt{C_{i,i}\cdot C_{j,j}}},\quad C_{i,j}(t) = \int_{0}^{T}S_{i}(t)\cdot S_{j}(t)\mathrm{d}t $$
- 整理 huwei 的实验仪器参数, 提出仪器需求;
- 尝试拟合自己的实验曲线, 得到扩散特征时间 $\tau_{\alpha}$;
- *搞清楚扩散方程的原理;
- *寻找一下专业的校准超声探头的技术手册, 学习其校准方法;
- 重新设计自己的曲线包络算法, 得到更理想的数据, 尝试得到衰减特征时间 $\tau_{\alpha}$;
- 重新学习如何测定相速度 $v_{\varphi}$.
12.12
尝试写出关联函数. 比较奇怪的是, 离散积分得到的值是 $[0, T]$ 上整个区间的, 应该只有一个值, 为什么能够得到一段 $R(i,j)$ 的时域分布呢? 没有搞懂是这个是如何定义出来的.
前面响应函数的测定, 在用连续波激励的时候存在一个问题, 就是只考虑了倍数关系, 没有考虑声阻抗实际上是一个复数, 所以真正计算的时候是需要处理相位信息的. 但是实际上, 我们可以做一个简单的心算:
$$ ka = \frac{2\pi}{\lambda_{E}}\frac{d}{2} = \frac{\pi f_{c}}{v_{E}} =\frac{\pi\cdot 2\times 10^{-2}\cdot 129\times 10^3}{10^3}\approx 7\gg 1 $$
而声阻抗表达式
$$ Z_{S} \approx \rho_{0}c_{0}S\frac{(ka)^{2}}{2} + i\rho_{0}c_{0}S\frac{8ka}{3\pi} $$
所以应当采取短波极限, 也就是大约为 $2$ 左右. 相位畸变几乎可以忽略不计. 感觉可以不用深究有关于声阻抗造成的相位畸变.
感觉要做的事情一时间太多, 稍微整理一下思路.
- DGM 信号处理
$\sqrt{}$ 自己写一个 correlation 函数.
- $\sqrt{}$ 搞清楚为什么会有时间上的分布.
- 学习文献 Low-Frequency Behavior of Beads Constrained on a Lattice
- $\sqrt{}$ 重新阅读文献 Probing intermittency and reversibility in a dense granular suspension under shear using multiply scattered ultrasound
- $\sqrt{}$ 尝试设计频域上的 correlation 函数, 并且尝试根据该函数确定延迟时间 $\tau$?
系综平均
- $\sqrt{}$ 放弃原先的 envelope 算法, 重新设计包络算法;
尝试使用 hilbert()?
事实证明, 无论是 hilbert 还是 envelop, 它们都已经尽力了. 还原为未处理信号会得到更加糟糕的图像. 目前已经可以根据后半段的信号得出其特征时间(衰减时间) $\tau_{\alpha}$, 品质因子 $Q$ 根据实验参数可以轻松得到了. 不管怎么样, 自己的
include代码库正在不断壮大.
将信号视为 $S(t) = e^{-\frac{t}{\tau_{a}}}f(t)$, 则对其进行对数处理得到
$$ \lg{S(t)} = \lg{f(t)} - \frac{\lg{e}}{\tau_{\alpha}}t $$
在经过足够长的时间后, $\lg{f(t)}\rightarrow 0$. 即可根据斜率 $k$ 得到特征时间 > $\tau_{\alpha}$.
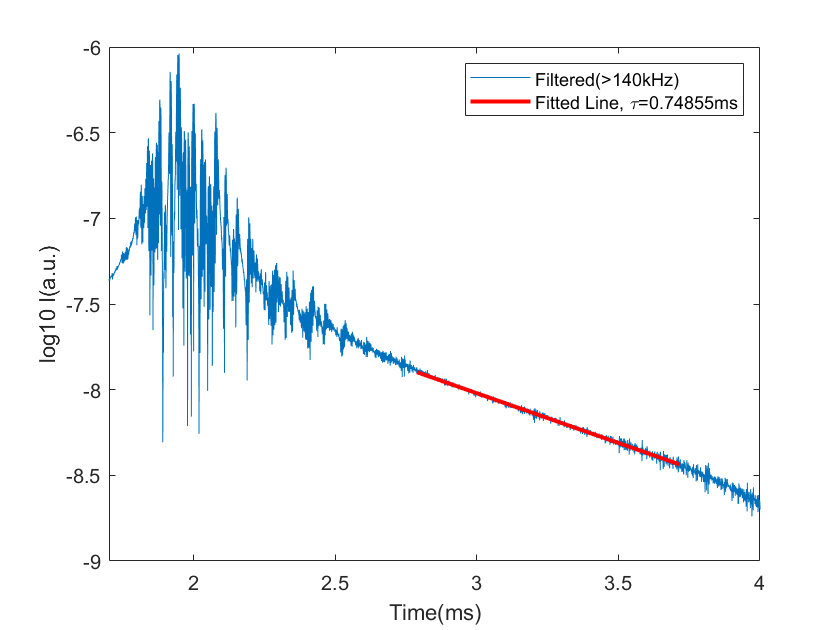
需要注意的是, 实际求出来的斜率实际上是带有虚数项的, 这是因为经过了校正, 滤波后的信号本身是带有虚数项的, 并且奇怪的是相位无法通过
abs()函数去除. 这是一个需要研究的问题.
相速度测定
-
重新阅读 Probing the effect of particle shape on the rigidity of jammed granular solids with sound speed measurements
-
$\sqrt{}$ 如何确定 $\tau$, 波前识别算法? dft 的 correlation 函数?
实际上, 相似性参数取峰值就是最成功的波前识别算法, 并且在 10000 的采样长度下, 其计算时间完全可以接受. 并且, 先计算交叉积确定波前, 也有助于选取真正的信号波段进行谐波展开.
- *学会声学扩散近似.
- 阅读 Experimental test of the diffusion approximation for multiply scattered sound
- 继续阅读 DIFFUSIVITY OF ULTRASOUND IN POLYCRYSTALS
瑞利散射的原始形式
$$ S(\lambda, \theta, h) = \frac{\pi^{2(n^{2} - 1)^{2}}}{2}\frac{\rho(h)}{N}\frac{1}{\lambda^{4}}(1 + \cos^{2}{\theta}) $$
$\lambda$: 入射光波长; $\theta$: 散射角度; $h$: 海拔高度; $n$: 空气折射率; $N$: 粒子数密度; $\rho(h)$: 强度比率, 海平面时为 $1$, $\rho(h)$ ~ $e^{h}$
- 非线性效应学习
- $\sqrt{}$ 许肖梅, 声学原理, 有限振幅的传播和畸变, 高次谐波的产生;
- $\sqrt{}$ 重新阅读文献 Transitional nonlinear elastic behaviour in dense granular media
- 贾小平 2019 暑校内容整理学习
- $\sqrt{}$ 学习带通滤波函数, 提取中心频率的信号强度
- 声学仪器调研
- huwei 文章阅读与整理;
- *超声信号的矫正
- *寻找有无专业的声学校正方法;
- *思考如何确定连续法的相位效应;
- 剪切带探测
- 贾小平 2019 暑校内容整理学习
- 阅读学习 Probing the shear-band formation in granular media with sound waves
12.18
工位办公室竟然养了一只猫.
12.19
昨天没有开组会, 倒是留出了一天的有效时间来阅读文献. 讲真, 如果组会频率下降, 就不用每周都要单独分配一天来做 PPT, 效率还提高了不少.
现在简单整理一下这周的任务计划:
- 发射信号设计
- 配合响应函数设计在频域上的高斯分布, 注意相位信息从而合理还原至时域信号
- *声学扩散近似
- 继续学习 Experimental test of the diffusion approximation for multiply scattered sound
- 声学仪器调研
- 重新学习 Effect of Amplitude and Duration of Cyclic Loading on Frictional Sliding Instability in Granular Media: Implication to Earthquake Triggering of Landslides, 收集其实验参数设计;
- 剪切带探测
- 贾小平 2019 暑校内容整理学习
- 重新学习 Probing the shear-band formation in granular media with sound waves
- 非线性声学
- 从更专业的角度学习. 学习钱祖文 非线性声学.
- Reference Stack
参考文献堆得越来越多, 但是看得却很少. 这里整理一下需要阅读的清单, 早点读完也早有体会.
12.20
今天开了周一没有开的组会, 这里总结一下除了上面的清单要做的事情:
- 重新整理有关于功率放大器的数据, 给出令人信服的放大效果展示;
- 和许家兆师兄沟通有关于放大器购买的事宜;
- 现在的非线性数据处理存在一些问题.
- 当开头的几个振幅较小(信噪比较低)时, 将难以有效寻找波前. 这只有在绘制出 wave train 图之后才会知道, 因此需要大改有关于波前识别和相似度参数的顺序寻找方法.
重新写一个通用性更强的非线性处理方法, 必须要考虑有关于信噪比过低的情况, 并且将对应的数据自动排除.
- 调研有关颗粒尺寸和共振频率的文章
12.21
询问了一下赵西梅老师有关于声学校正的看法, 没有得到太多有用的信息.
比较麻烦的是 BNC 三通转接头也被还回去了, 现在只能紧急订购几个, 在到货之前没办法做实验了.
12.25
- $\sqrt{}$ 重构有关非线性响应的代码, 要求识别并且排除信噪比较低的数据, 自动从合格数据开始分析.
现在的代码已经可以自主选择非线性分析起点了, 可以说是智能程度大大增加了. 另外, 需要注意的是, 虽然在做实验的时候可以把 $\delta V_{\text{input}}$ 取小一点, 但是这对于改善信号的信噪比, 也就是说有效数据起点没有任何用处. 所以真正需要的是那些在小振幅就可以很高效地传播信号, 自己用的超精细颗粒/精细颗粒无意间让弹性模量变得很小, 这显然是不利于实验正常进行的.
也就是说竟然无意间达到了 “开局即巅峰” 的境界, 玻璃珠 + 90khz 效果最好. 既然如此, 可以再尝试一下 2mm 铁质颗粒或者其他颗粒. 或者加大一下压强, 效果应该也会明显一些.
明天把买的转接头拿到实验室重新搭一下线路, 然后就是仔细读一下有关声学润滑和诱导雪崩的文章, 之前看了但是没有看懂, 看懂了就可以设计新一轮实验了.
12.26
今天拿到了转接头, 一看发现型号根本不对, 怪不得那么便宜, 可谓是便宜没好货.
-
重新购买转接头. 非线性效应只能先将就着做;
-
联系许家兆师兄看如何购买信号放大器;
-
重新阅读润滑和雪崩的文章, 考虑如何设计参数;
12.27
今天阅读了高时间分辨率的文章, 里面谈及了有关主滑移和微滑移的频谱相似性. 直觉告诉我, 这东西可能和时域相关性是等价的, 但是还没有使用傅里叶变换进行严格证明.
已知对于两个信号 $S_{i}(t)$ 和 $S_{j}(t)$, 其时域相似性被定义为
$$ \begin{aligned} \Gamma_{ij}^{t} = \frac{\int_{-\infty}^{+\infty}S_{i}(t)S_{j}(t)\mathrm{d}t}{\sqrt{\int_{-\infty}^{+\infty}S_{i}^{2}(t)\mathrm{d}t}\sqrt{\int_{-\infty}^{+\infty}S_{j}^{2}(t)\mathrm{d}t}} \end{aligned} $$
而根据傅里叶变换, 有
$$ S(\omega) = \int_{-\infty}^{+\infty}S(t)e^{-i\omega t}\mathrm{d}t $$
我们可以引入类似定义的频谱相似性
$$ \begin{aligned} \Gamma_{ij}^{\omega} = \frac{\int_{-\infty}^{+\infty}S_{i}(\omega)\bar{S_{j}}(\omega)\mathrm{d}\omega}{\sqrt{\int_{-\infty}^{+\infty}S_{i}^{2}(\omega)\mathrm{d}\omega}\sqrt{\int_{-\infty}^{+\infty}S_{j}^{2}(\omega)\mathrm{d}\omega}} \end{aligned} $$
注意这里取内积时, 一个信号需要取共轭.
能否证明 $\Gamma_{ij}^{t}$ 和 $\Gamma_{ij}^{\omega}$ 的等价性?
查了一下, 这其实是一个非常经典的问题, 其解决思路是使用 Parseval’s theorem, 其也被理解为 能量定理:
$$ \int_{-\infty}^{+\infty}S_{i}(t)\bar{S_{j}}(t)\mathrm{d}t = \frac{1}{2\pi}\int_{-\infty}^{+\infty}S_{i}(\omega)\bar{S_{j}}(\omega)\mathrm{d}\omega $$
特别地, 当 $i = j$ 时, 有
$$ \int_{-\infty}^{+\infty}|S(t)|^{2}\mathrm{d}t = \frac{1}{2\pi}\int_{-\infty}^{+\infty}|S(\omega)|^{2}\mathrm{d}\omega $$
所以
$$ \begin{aligned} \Gamma_{ij}^{t} &= \frac{\int_{-\infty}^{+\infty}S_{i}(t)S_{j}(t)\mathrm{d}t}{\sqrt{\int_{-\infty}^{+\infty}S_{i}^{2}(t)\mathrm{d}t}\sqrt{\int_{-\infty}^{+\infty}S_{j}^{2}(t)\mathrm{d}t}}\\ &= \frac{\int_{-\infty}^{+\infty}S_{i}(t)S_{j}(t)\mathrm{d}t}{\sqrt{\frac{1}{2\pi}\int_{-\infty}^{+\infty}|S_{i}(\omega)|^{2}\mathrm{d}\omega}\sqrt{\frac{1}{2\pi}\int_{-\infty}^{+\infty}|S_{j}(\omega)|^{2}\mathrm{d}\omega}}\\ \end{aligned} $$
我们录制得到的 $S(t)$ 都是幅值信号而没有频域上的相位信息(即都是实信号), 所以可以令 $S_{j}(t) = \bar{S_{j}}(t)$, 从而有
$$ \begin{aligned} \Gamma_{ij}^{t} &= \frac{\int_{-\infty}^{+\infty}S_{i}(t)\bar{S_{j}}(t)\mathrm{d}t}{\sqrt{\frac{1}{2\pi}\int_{-\infty}^{+\infty}|S_{i}(\omega)|^{2}\mathrm{d}\omega}\sqrt{\frac{1}{2\pi}\int_{-\infty}^{+\infty}|S_{j}(\omega)|^{2}\mathrm{d}\omega}}\\ &= \frac{\frac{1}{2\pi}\int_{-\infty}^{+\infty}S_{i}(\omega)\bar{S_{j}}(\omega)\mathrm{d}\omega}{\sqrt{\frac{1}{2\pi}\int_{-\infty}^{+\infty}|S_{i}(\omega)|^{2}\mathrm{d}\omega}\sqrt{\frac{1}{2\pi}\int_{-\infty}^{+\infty}|S_{j}(\omega)|^{2}\mathrm{d}\omega}}\\ &= \Gamma_{ij}^{\omega} \end{aligned} $$
前面我们在进行相似性分析的时候没有考虑到这一点, 所以将内积定义为复数域的内积就完美了.
$$ \begin{aligned} &\int_{-\infty}^{+\infty}S_{i}(t)\bar{S_{j}}(t)\mathrm{d}t\\ &=\int_{-\infty}^{+\infty}\left[\frac{1}{2\pi}\int_{-\infty}^{+\infty}S_{i}(\omega)e^{i\omega t}\mathrm{d}\omega\right]\left[\frac{1}{2\pi}\int_{-\infty}^{+\infty}\bar{S_{j}}(\omega^{\prime})e^{-i\omega^{\prime} t}\mathrm{d}\omega^{\prime}\right]\mathrm{d}t\\ &= \frac{1}{2\pi}\int_{-\infty}^{+\infty}S_{i}(\omega)\frac{1}{2\pi}\int_{-\infty}^{+\infty}\bar{S_{j}}(\omega^{\prime})2\pi\delta(\omega - \omega^{\prime})\mathrm{d}\omega^{\prime}\mathrm{d}\omega\\ &= \frac{1}{2\pi}\int_{-\infty}^{+\infty}S_{i}(\omega)\bar{S_{j}}(\omega)\mathrm{d}\omega \end{aligned} $$
即证
$$ \boxed{\int_{-\infty}^{+\infty}S_{i}(t)\bar{S_{j}}(t)\mathrm{d}t = \frac{1}{2\pi}\int_{-\infty}^{+\infty}S_{i}(\omega)\bar{S_{j}}(\omega)\mathrm{d}\omega} $$
记录一下明天要做的事情:
-
重新购买转接头. 非线性效应只能先将就着做;
-
联系许家兆师兄看如何购买信号放大器;
-
重新阅读润滑和雪崩的文章, 考虑如何设计参数;
-
写一个可定义 time_window 的时间-频率热图, 用于分析时域上各个阶段主要信号的频率特征.
12.28
我们自己的探头只能检测到压缩波吗? 能够检测到剪切波吗?
现在也算是做了一点实验, 也学了一点声学方法, 现在简单总结一下. 这里就省去引言在内的无关紧要的废话, 只谈文章脉络和发展思路. 已经做过的就简单一些, 还没有做过的就补充实验设计的方法和思路.
环形恒速剪切过程中颗粒介质粘滑破坏过程中的超声信号研究
- 致密介质中的声学传播
- 相干波和散射波
- 超声扩散近似
- 声速与压力之间的关系(仿射变换为等效介质)
- 声信号非线性效应揭示结构是否变化
- 提出相似性参数
- 提出相对动态应变 $r_{s} > 3\%$ 与结构变化的关系
设计频域上高斯分布的波形并转换到时域上(记得使用响应函数预修正)
高斯脉冲信号频率成分集中, 且主峰两边的小峰都可以得到极大抑制
(X 光探测的弊端: 应用于真实的三维不透明颗粒材料比较困难) 使用剪切波探测剪切模量在临近解堵塞(unjamming)的特定行为;
-
测量波速
-
- 共振法. 不同的输入电压-不同的共振峰曲线(可以只在峰附近进行精细测量). 响应曲线需要归一化. 电压增加, $f_{r}\downarrow$, $v\downarrow$;
-
- 行波法(飞行时间法).
-
有效压力和模量变化之间的关系
-
应变阈值 $\varepsilon_{T}$. 低于时, 应变振幅不改变共振频率和模量. 有效压力 $\uparrow$, $\varepsilon_{T}\uparrow$.
-
慢动力学. (模量受软化后的缓慢恢复)
触发机制:1. 有效压力低; 2. 临界状态; 3. 动态应变振幅 $> 10^{-6}$
- 剪切带的声学探测
远离壁边界的剪切应变区域
实验装置要求
- 剪切盒, 恒速剪切装置, 剪切力测量装置, 恒定法向应力
- 水平位移和垂直位移传感器, 测量介质剪胀性
- 玻璃珠(材料密度, 剪切模量, 泊松比…)
- 制备协议(雨落法)
- 信号参数: $4\mu\text{s}$ 短脉冲激励, 剪切波
由于是恒速剪切, 所以剪切位移和时间其实是等价的. 在剪切过程中发射声信号并进行相关性检测. 从应力降可以看出不同层次的滑移(主滑移/快滑移, 小滑移/慢滑移, 以及粘连过程)
相关性骤降说明结构的变化. PhysRevE.85.051302 和 10.1073/pnas.2305134120, 前者是同时检测 相关性 和 比应力, 后者没有关心相关性, 而是从 应力-高度-波形 来分析的. 自己进行实验室, 可以选择其中可行性更好的几个来进行同步分析.
- 首次剪切的S声速-剪切位移(时间)图 和 同向/反向重复剪切的 S 声速-剪切位移(时间)图
同向和反向的重复剪切中, 声速几乎不变
剪切载荷使得应力和模量张量的主轴旋转, 等效于降低弹性模量
注意这里采用了 EMT 近似, 即 $\lambda\gg d$
-
首次剪切 和 循环剪切 形成的力滞回线/速滞回线
-
1Hz 的声发射频率, 记录响应波形与近邻相关性
放大应力-剪切位移(时间)图, 与声信号同步对比. 快滑移-大幅应力降-相关性骤降; 慢滑移-小幅应力降-相关性小幅降低, 粘滞-应力缓升-相关性在 1 附近小幅波动, 小降表示有轻微的结构变化
- 超高时间分辨率采样, 超声视角监测粘滑过程
- 无导向高度-电压传感器和弹簧回位传感器的采集对比(样品高度)
- 时间-频率图热图监测过程中的声学成分(短时傅里叶变换)
主要是配合 应力 和 样品高度 的同步采集, 分析各个子过程的频域特征
- *时域相似性和频域相似性的等价性
快/慢滑移具有相似的频率-振幅曲线. $\Gamma_{ij}^{f} = \Gamma_{ij}^{t}$
截止频率
- 使用颗粒自由落体碰撞近似颗粒间的摩擦过程, 进行频谱分析
不同高度自由落体碰撞引起的声信号频谱对比
- 声学润滑, 共震, 诱导雪崩, 模量软化
-
超声剪切引起表观静摩擦系数降低. 将振动理解为等效温度
-
振动诱发的低于雪崩角的雪崩
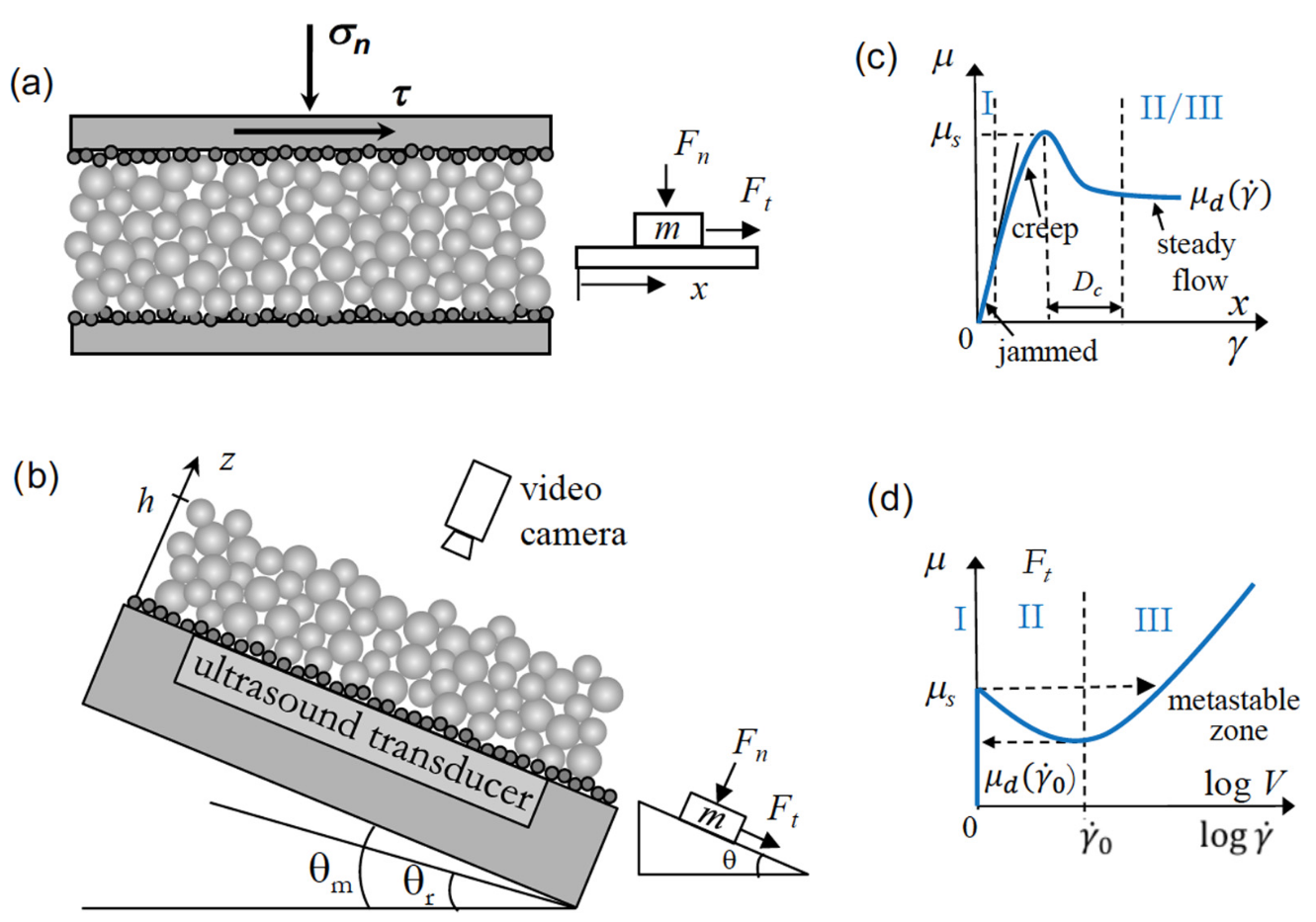
- 非线性效应
使用精细颗粒效果不太好, 因为散射太强. 应当按照玻璃这样较硬, 相对摩擦强的颗粒
- 颗粒碰撞声谱研究
需要克服 RAEM1 采样困难的问题.
- 实验装置需求整理
- 信号放大器(至少能到 $300 V$)? 其实只有 $30\text{V}$
- 连续, 实时, 可存储采集卡. (可以先研究一下怎么用示波器导出数据)
- 响应效率在频域上尽量平均的探头
- 可以产生和接受剪切波的探头
- 剪切带形成装置
- 应变测量装置(声称使用的是光学干涉测得, 但是为什么在颗粒中也可以得到? 使用了什么线性近似吗?)
- 剪切和声发射同步完成, 每秒钟都自动存储一次有效的声信号, 与此同时接受应力信号.
目前没有理解到的是, 为什么一个平面传感器, 可以检测到剪切波的信号.
12.29
和老师进行了交流.
调研各个厂家的探头
询问技术有没有更硬件的控制方式
更深入地阅读有关探测剪切带的问题, jia 是如何做出关于剪切带从无到有产生的推测
询问代学亮师兄的剪切盒子, 配置好有关剪切力传感器等物件, 尝试进行同步性分析
咨询一下技术有关于探头的有效探查频域在物理上是如何实现的
和王鑫师兄聊天后得到建议与经验
参考课表进行提前选课(软物质, 博资考需要注意高量和热统)
多找袁后非师兄, 邢义师兄, 曾志坤师兄交流, 询问一下想法是否可行, 看下有什么参考意见. 不要偷懒
优先推进自己的项目, 有时间再看看小组学习的知识;
推荐阅读 granular media 和 组里的基金本子, 师兄师姐的毕业论文也是值得参考的对象.
研究致密堆积的时候, 需要有效利用相似度定义波前进行 时间平均. 这在处理非线性效应的谐波分量时也非常好用.
高斯轮廓拟合, 得到波形图. 这样处理的意义是什么? 因为有效信号是低频波所以需要进行高斯模糊, 去除杂乱的高频成分?
1 月
1.3
研究一下有关于传感器在和剪切盒耦合的时候应该怎么处理. 那个耦合剂能起到什么作用? 老师的意见是可能会起到低通的作用, 实际上会是什么作用?
- 有关于滞滑过程需要注意的几个参数, 后续处理信号的时候需要特别设计算法进行识别.
- 滞滑事件计数
- 应力降
- 事件时间间隔
成核的那篇文章使用的是将后两者的时间平均值作为特征量.
-
时频热图的绘制, 成核文章是使用的 Hilbert-Huang 变换. 需要和自己临时使用的 spectrogram() 函数进行对比. 这个变换主要是用于去除噪声
-
热度图不太便于观察截止频率, 所以可以绘制 $f_{max}-time$ 图像便于观察.
-
在对滑移产生的声信号进行频域特性统计之前, 至少应该按照对应机械信号(比如最典型的应力降)进行预先的分类.
-
做完实验记得筛查一下是否出现了颗粒破碎的情况.
-
力学传感器的采样频率比较高的时候, 可以考虑使用时间窗口法进行近邻平均, 从而使得信号更平滑. 考虑使用加权平均: 使用抛物线权重对窗口内信号进行赋权.
1.4
今天在代学亮师兄的帮助下熟悉了剪切盒的使用, 也成功做出一条应力-应变曲线, 但是目前还存在不少问题.
首先记录一下实验仪器的参数
- 电机
最大活动范围是 $150\text{ mm}$, 剪切速度通过 $\text{pps}$ 定义. 粗测了一下 $10\text{ pps}$ 对应的剪切速度 $\approx 37\mu\text{m/s}$.
贾老师的剪切速度可以达到 $0.6\mu\text{m/s}$, 这还是相对于颗粒尺度为 $\sim 700\mu\text{m}$. 我们相对剪切速度为贾老师的 $10$ 倍左右.
可以使用 jog 或者保存的配置文件来调整电机的参数. 一个移动单位对应 $0.1\text{ mm}$.
- 力学传感器
最快的采样频率为 $1/\tau = 1/0.0005 = 2000\text{ Hz}$. 虽然这个采样频率已经算是比较高, 但是对于 $10\text{ MHz}$ 还是相形见绌. 师兄还告诉我, 这个采样频率可能对应的时间间隔相对于现实世界的时间流逝而言未必准确. 即使如此, 在放大之后观察其曲线, 仍然会有一定的粗糙感.
- 剪切盒
目前的问题:
-
缺少较短的连杆&套筒, 还需要采购一下多通道采集卡. 三头 BNC 转接头也需要尽快就位;
-
无法观察高度变换. 可能需要类似于限位器的装置, 能够保持表面平整的同时还可以具有高度测量的作用.
-
目前仍然欠缺长时间稳定的声学测量手段.
1.5
恍然大悟. 高斯调制的原理原来如此简单.
高斯分布定义为
$$ f(x) = \frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(x-\mu)}{2\sigma^{2}}} $$
简写为
$$ f(x) = \mathcal{N}e^{-\alpha x^{2}} $$
$\alpha = \frac{1}{2\sigma^{2}}$, $\mathcal{N} = \sqrt{\frac{\alpha}{\pi}}$. 暂时不考虑平均值 $\mu$. $\sigma$ 调制宽度, 这个可以自己用实验慢慢熟悉.
傅里叶变换:
$$ \widetilde{f}(k) = \mathcal{N}\int_{-\infty}^{+\infty}e^{-\alpha x^{2}}e^{-ikx}\mathrm{d}x = \mathcal{N}\int_{-\infty}^{+\infty}e^{-\alpha x^{2} - ikx}\mathrm{d}x $$
约定
$$ \alpha x^{2} + ikx = \alpha (x + c)^{2} + d\Rightarrow c = \frac{ik}{2\alpha}, d = -\frac{k^{2}}{4\alpha} $$
即有
$$ \widetilde{f}(k) = \mathcal{N}e^{-\frac{k^{2}}{4\alpha}}\int_{-\infty}^{+\infty}e^{-\alpha\left(x + \frac{ik}{2\alpha}\right)^{2}}\mathrm{d}x $$
换元 $x^{\prime} = x + \frac{ik}{2\alpha}$, 有 $\mathrm{d}x^{\prime} = \mathrm{d}x$:
$$ \widetilde{f}(k) = \mathcal{N}e^{-\frac{k^{2}}{4\alpha}}\int_{-\infty + \frac{ik}{2\alpha}}^{+\infty+\frac{ik}{2\alpha}}e^{-\alpha x^{\prime 2}}\mathrm{d}x^{\prime} $$
令
$$ I = \int_{-\infty + \frac{ik}{2\alpha}}^{+\infty+\frac{ik}{2\alpha}}e^{-\alpha x^{\prime 2}}\mathrm{d}x^{\prime} $$
含变区间的积分求导
$$ I(x,t) = \int_{f(t)}^{g(t)}y(x)\mathrm{d}x $$
则
$$ \frac{\partial}{\partial t}I(x,t) = \frac{\partial}{\partial t}\int_{f(t)}^{g(t)}y(x)\mathrm{d}x = \frac{\partial}{\partial t}\left(Y[g(t)]-Y[f(t)]\right) $$
而
$$ \frac{\partial Y(x)}{\partial t} = 0 $$
所以有 $\frac{\partial I}{\partial k} = 0$, 所以不妨设 $I = I(k=0)$. 于是有 $\mathcal{N}I = 1$:
$$ \widetilde{f}(k) = e^{-\frac{k^{2}}{4\alpha}} $$
这表明, 实空间中的高斯分布在动量空间上仍然是高斯分布, 且只有高斯分布满足这样的性质.
回到调制信号上, 假设中心频率为 $f = 150\text{ kHz}$, 定义
$$ S(t) = \sin{(2\pi ft)}\cdot G(t) = \sin{(2\pi ft)}\cdot \frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(t-\mu)^{2}}{2\sigma^{2}}} $$
$\mu$ 一般与实际实验中的循环数有关, 即一般都是取其一半所对应的时间
参考自 卷积定理
$S(t)$ 进行傅里叶变换:
$$ S(\omega) = \int_{-\infty}^{+\infty}S(t)e^{-i\omega t}\mathrm{d}t $$
记高斯函数 $G(t)$ 的傅里叶变换为 $G(\omega)$, 正弦函数的傅里叶变换为 $\delta(\omega - 2\pi f) + \delta(\omega + 2\pi f)$. 根据卷积定理有
$$ S(\omega) = G(\omega)\cdot(\delta(\omega - 2\pi f) + \delta(\omega + 2\pi f)) = G(\omega - 2\pi f) + G(\omega + 2\pi f) $$
这就不难理解了: 在高斯分布上乘 $f$ 的单色波, 等效于将高斯分布在频域上移动至 $2\pi f$ 处.
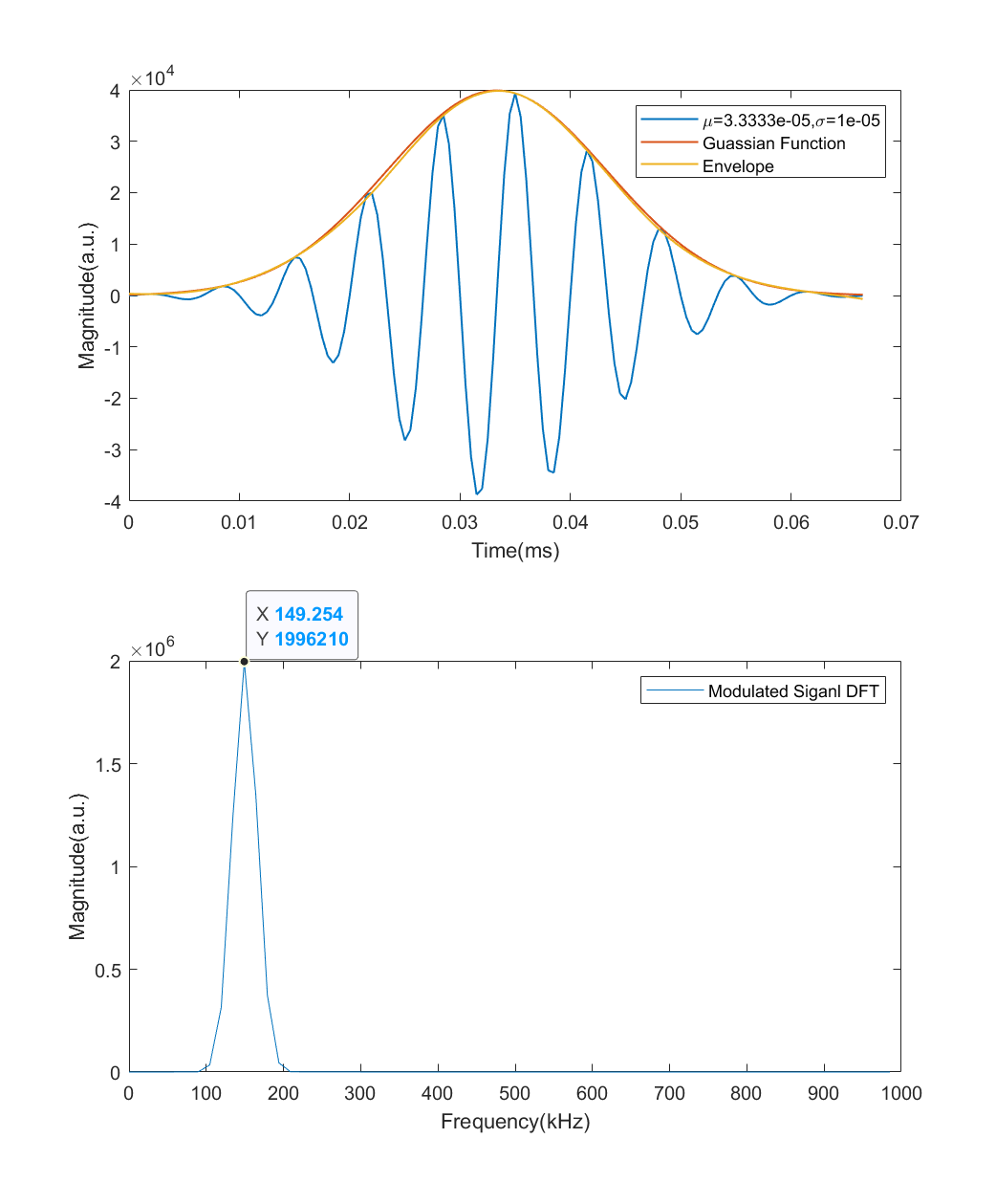
目前的两种方案:
-
监测法. 记录整个剪切过程 (约 $1000\text{ s}$) 的声学信号. 目前还在探索如何使用 RAEM1 做到这一点.
-
探测法. 等待后续剪切盒的设计和使用. 可能需要涉及对容器顶/底进行挖孔测试.
以 $1\text{ Hz}$ 或者 $2\text{ Hz}$ 频率发射试探信号, 记录这些信号.
- 启动信号发生器
- 原则上的发射间隔为 $1\text{ s}$ 或者 $0.5\text{ s}$.
- SWAE 启动观测
- 在规定的采样时间($t_{0}, t_{0} + 1, t_{0} + 2, \dots$)附近选取数据完整的 $5\text{ ms}$ 采样, 记录其到达时间以与现实时间的时间进行对时
-
启动应力传感器(注意回调为 $0$)
-
启动步进电机
- 剪切距离是可控的, 注意配合应力传感器的计时来确定剪切速度.($37\mu\text{m/s}$ 未必是每一次 $10\text{ pps}$ 都能对应的)
计划:
- 力学信号处理
- 如何在数学上定义滞滑事件, 对滞滑事件进行标记与统计;
- 记录事件之间的时间间隔, 并且对其进行统计;
- $\sqrt{}$ 学习时间窗口配合加权平均(考虑分别使用抛物线权重和高斯权重)对曲线进行平滑处理;
只是看不太出来各个方法的优劣是什么. 只有一点是确定的: 力学传感器的力学精度只有 $0.1\text{ N}$, 如果更精细一些就好了.
- $\sqrt{}$ 双轴法绘制实验图像. $x$ 轴: 时间/位移(Displacement); $y$ 轴: 应力/相似性参数;
- $\sqrt{}$ 学习如何对局部图像进行放大的绘图方法.
- 连续声学采集方法
- 再次尝试使用 RAEM1 采集规定时间的信号, 并且保证高可重复性
为什么设定采集 $10\text{ s}$ 的数据, 表格生成出来却对应了 $25\text{ s}$ 或者 $7\text{ s}$ 的数据点?
- 物资采购
- 连杆和套筒
- 多通道采集卡
- 三母头的 BNC 信号转接头
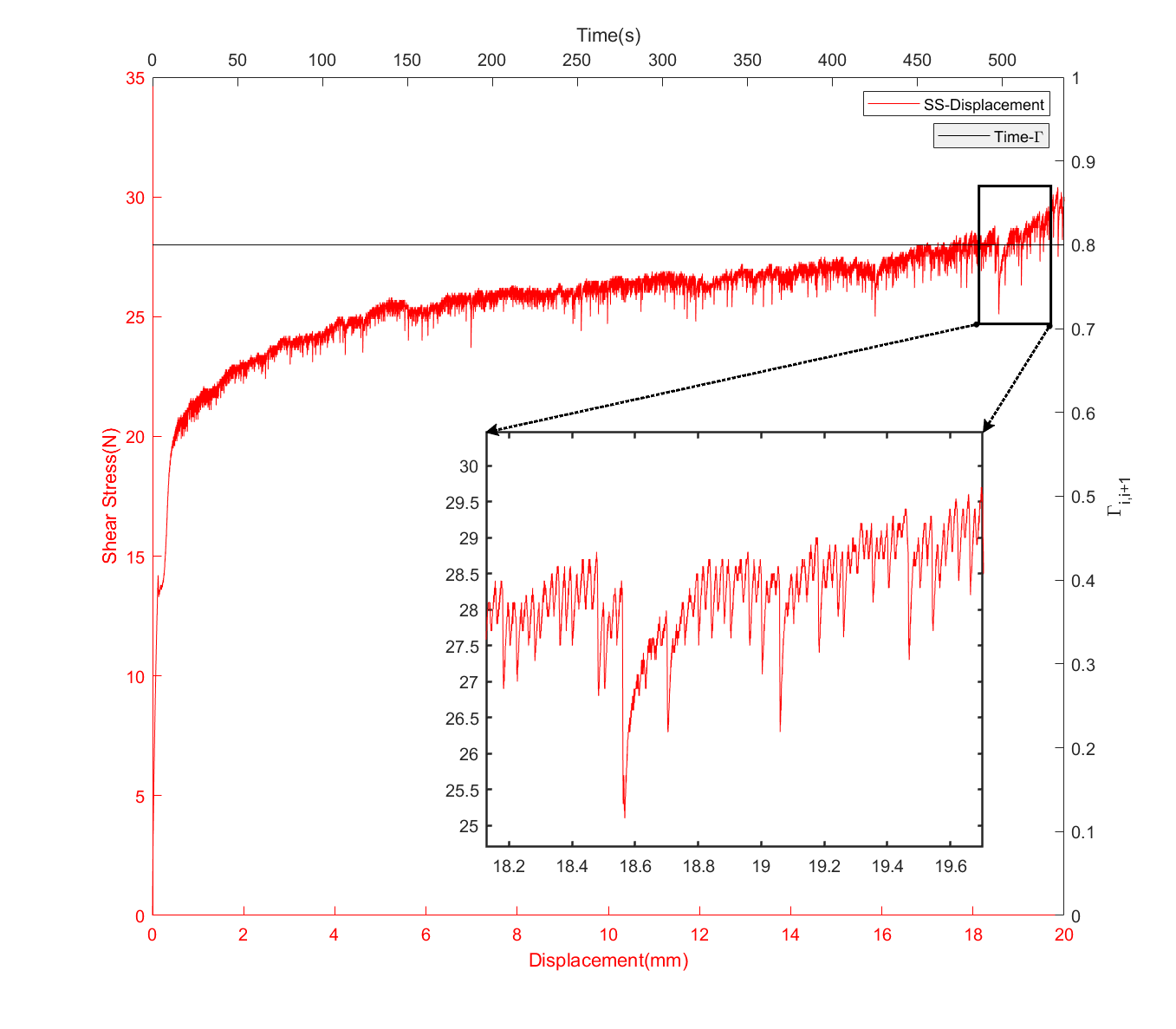
虽然现在 $\Gamma_{i,i+1}(t)$ 还没有办法做出来, 但是现在作图工具已经备齐. 虽然这个放大工具好用, 可惜对于双 $y$ 轴的放大效果还是不行, 需要后续手动调整. 目前把四个轴都占用上, 反而触发 bug 使其放大失败失败(没错, 失败两次!), 从而做出还不错的效果.
后续把 $\Gamma_{i,i+1}(t)$ 做出来之后, 这种示意图可能就需要自己手动写代码控制了.
1.7
记录一下组会上的一些质疑和建议
目前对于 micro- 的定义仍然不算清晰, $0.1\text{ N}$ 可能包含了较多的噪声, 使得记录的 micro 事件数量偏多; 后续应该使用另一种直方图绘制方法, 将这些 $0.1\text{ N}$ 的信号标记出来.
阅读学习老师推荐的
Sounds of Failure: Passive Acoustic Measurements of Excited Vibrational Modes.思考如何构造更好的剪切盒装置;
测试更大的剪切形变($\sim 4\text{ cm}$)
记录一下剪切盒的尺寸参数.
1.8
当探头铺设到剪切盒底部时, 没有记录到有效的声学信号.
忘记先和师兄商量剪切盒能不能开洞就已经执行了, 真是脑子短路了.
PS. 后面还得知误拆了卢海洋师兄的剪切加压装置, 也是非常抱歉. 在开学后的组会上私下再次道了歉, 希望之后没有再次事件.
3 月
3.3
简单写一下可能的仪器采购清单
先抄写一下参考文章所用的 NI 仪器.
- 滞滑成核与破坏
连续采集: NI compact DAQ, PXle1084, BNC-2110;
AE 触发采集: Micro-II Express-8
信号: 传感器, 前置放大器
采集卡: 四通道高速采集模块 BNC-2110
- 高时间分辨率采集信号
3.4
恢复手感用的实验. 加入放大器的因素.
最大加入放大器后的不畸变电压值: 150 V. 可能的问题在于: 无法比较自由的调整放大电压间隔.
SURUGA DSCONTROL-WIN
Force Recorder Standard
软件迁移到了自己的电脑上, 但是因为缺线所以还没有实际做出电机的效果.
3.7
把装置的图纸画出来了, 并且已经和制作装置的师傅联系上了, 比较蛋疼的一点是真正制作的时候才知道 板材实际上只有 $5,6,8,10,12\text{ mm}$ 的尺寸. 还好师傅说不用重新画图, 只需要稍微改一下厚度就可以投入生产了.
还有需要注意的一点是, 开 M4 螺纹孔实际上并不需要将螺纹孔打通, 只需要在对应位置留出一定的空间就可以了. 公差在画图的时候也是需要考虑的, 师傅帮忙考虑的是活塞留出半径 $\pm 0.25\text{ mm}$, 支撑柱留出半径 $\pm 0.5\text{ mm}$. 到此就算是完成 DGM 装置的设计和交付了, 明天就会收到报价.
另外还和导师讨论了有关多通道采集卡的事情, 最后得到的共识就是贵的实际上不是采集卡(BNC-2110)而是机箱(PXle1084), 机箱将数据上传到电脑上, 重量级价格(58000+), 而老师听说的价格是十万, 这一点我尚不清楚到底是怎么回事, 应该再具体整理一下各文献中所使用仪器的具体价格. 在 NI 方面, 除了索要报价外, 最好是看看能不能申请到样机; 声学探头则是主要看一下我们自己用的几千块钱的探头和 Micro-II Express-8 的探头性能差距到底在哪里.
简单写一下要具体做的实验系列
- 外部应力下的致密颗粒介质
- 两种声波以及对应声速的测量(TOF, 飞行时间法);
注意声电转变的耗时. 方法: face-to-face time 测量;
- 发射信号和接收信号参考点的选取问题;
高斯调制若干循环的正弦波列的积极意义(实际实验上需要预先除以响应函数);
考虑颗粒尺度和波长之间的关系. (长波产生相干波, 短波产生散射波)
测量介质的共振频率;
-
*容器边界条件对于接收信号的影响;
-
声速和外部应力的关系($\sim p^{1/6}$);
控制压强(应力)大小, 观察声速的变化;
- 散射波的扩散模型
$$ \partial_{t}I -D\nabla^{2}I + \frac{I}{\tau_{\alpha}} = \delta(z)\delta(t) $$
滤波处理的合理性;
关注平均自由程 $l$ 以及品质因子 $Q$;
干湿堆积对于界面耗散/品质因子的影响;
- 颗粒介质中的非线性
流体中的非线性(黏性, 热传导…), 以及颗粒介质的迁移
探头在频域上的响应函数的测定(注意考虑不同测定方式带来的影响);
最关键的公式:
$$ u_{n\omega}\sim u_{\text{in}}^{n} $$
测定颗粒介质中的不可逆机制(测定声波中的谐波分量和声源振幅的关系, 以及关联函数 $\Gamma_{i,i+1}^{t}$ 随实验事件次数的变化情况);
利用 $\Gamma_{i,i+1}(\tau)$ 确定绝对定义的波前;
- 剪切带探测
- 力学信号的处理方法
两种平均方法(对高频信号使用, 线性平均和抛物线权重平均)
滞滑事件的定义与统计(根据 micro-slip 数预言 failure 发生的可能性)
- 声学信号的处理方法
关联函数/相似性参数的延拓(Parseval 定理): $\Gamma_{ij}^{t}\equiv \Gamma_{ij}^{\omega}$
- 剪切盒
被动探测: 记录含时力学信号以及伴随的声发射(AE)事件;
主动探测: 记录含时力学信号, 以某频率发射试探信号并计算相邻相关参数, 得到含时相关函数;
- 环形剪切
记录高度变化(dilatancy, 剪胀性), 声学信号(频域, 累计能量, 含时频域函数(短时傅里叶变换))
3.18
- 测量 face-to-face time
peak-to-peak: 14.2 $\mu$ s wave front-to-wave front: 4.08 $\mu$ s
3.19
face-2-face time, 信号参数: 100kHz, 10Vpp, 4循环
- 考察不同参考点(设第一个峰值为 $A_{1}$, 分别取 $A_{1}/10, A_{1}, 0$) 对应的事件为参考点, 研究对应声速的变化, 确定最佳声速参考点选取
参考文章: Sound pulse broadening in stressed granular media, 10.1103/PhysRevE.91.022205
实验条件
装置自重: 1031.2 g
容器参数: 内径 9cm, 容器限高 12.5 cm
顶部活塞自重: $\sim 260$ g.
参考文章不同距离取点: 10
第一组实验, 使用 5mm + 6mm 双分散钢珠, 测试声学信号是否明显
第二组实验, 使用 5mm + 6mm 双分散玻璃珠, 可以观察到显著信号.
偶然理解了 Tektronix 示波器的时间平均功能, 得到了无法想象的完美曲线, 我也算是理解到贾小平老师那么干净的图像究竟是怎么得到的了.
那么现在再根据示波器的双通道同步采集, 再加上事后对于波形信号文件的处理, 得到该实验想要的曲线将会易如反掌.
设定示波器的平均次数: 128
发射信号参数设定: 30 kHz, 5 循环 10 Vpp(10dB 增益), 发射间隔 5ms 通过 TekScope 软件导出了示波器的数据, 目前得到的都是静态数据, 不知道后续会不会有什么多通道采集卡的替代方法.
受压的玻璃珠堆积对应的飞行时间法测声速图像.
使用重物的质量: 5.4kg 对应的压强:
$$ \frac{Mg}{\pi r^{2}} = \frac{(5.4+0.26)\times 9.8}{3.14\times (4.5\times 10^{-2})^{2}} = 8719\text{ Pa} $$
通过呕心沥血写出来的波前和波峰搜索算法投入使用, 最后得到了不同参考点随距离变化的图像.
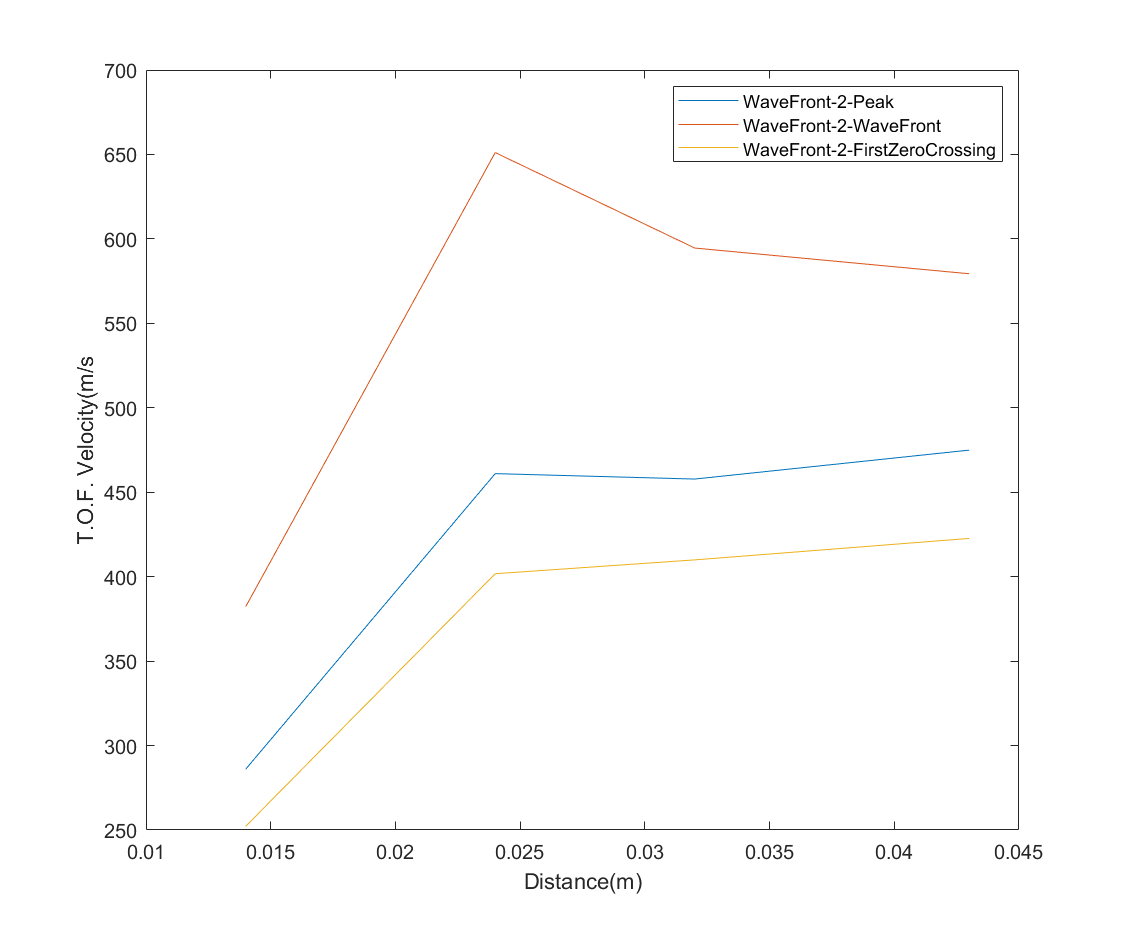
由此可知在较短约化长度的情况下, 声速测量误差较大, 排除一开始的误差后, 得到的图像和贾小平教授的结论基本相近.
更详细的数据可能需要换用更小更多的颗粒, 并且需要配备相应的前置放大器.
3.24
- 声速与外部应力的关系
第一组.
2mm 钢珠 - 10 mm.
信号参数: 30kHz-5循环正弦波列, 10Vpp(+10dB), 触发间隔 10ms.
依次称量放上去的金属块质量, 每次的应力是之前放上的金属块质量之和
然而,人们观察到,在堵塞球体堆积中,低 $P$ 值时声速为 $V\propto P^{1/4}$,高 $P$ 值时声速为 $V\propto P^{1/6}$(我们将证明本研究中的实验仍处于 $V\propto P^{1/6}$ 阶段)
$P^{\alpha}: P\uparrow, \alpha\downarrow, p = 1/\text{slope} = \frac{1}{\alpha}\uparrow$
在自己的实验中, 施加的压力应当始终都是较小的.
3.26
注意多次测量取平均值, 并且加上标准差计算而来的误差棒
- 相速度测量
令传播信号为
$$ s(x,t) = A_{0}e^{-\alpha x}e^{i(\omega x/{V_{\varphi}(\omega)} - \omega t)} $$
频域上的衰减函数 $\alpha(\omega)$
$$ \alpha(f) = \frac{1}{x_{2} - x_{1}}\ln{\frac{S_{1}(f)}{S_{2}(f)}} $$
频域上的相速度
$$ V_{\varphi}(f) = 2\pi f\frac{\Delta x}{\varphi_{2}(f) - \varphi_{1}(f)} $$
之前为了测量飞行时间存的文件实际上并不太适用于计算相速度.
波形文件需要采集的时间长度尽可能完整(包括相干波和散射波); 设计算法, 只选取相干波而筛去散射波;
使用 到达时间-距离 进行拟合, 这种方法比较接近传统的声速测量方法.
Elastic wave propagation in confined granular systems PHYSICAL REVIEW E 72, 021301 (2005)
模仿实验的数据:
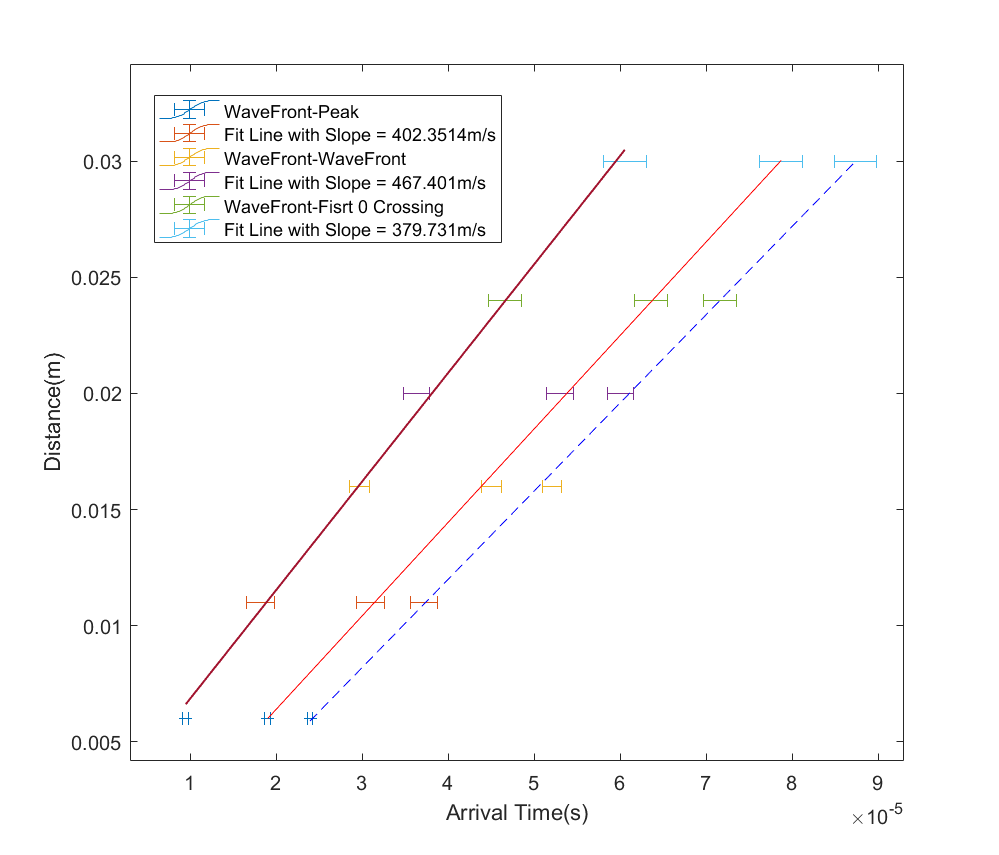
可以看到虽然选取的参考点不同, 但是在距离上的传播是线性的, 归根到底是相干波中具有不同的频率成分, 不同的频率具有不同的波速. 为了更准确全面地描述这个 Sound Pulse Broadening in Granular Media 的过程, 最好的方法仍然是测量信号的相速度.
$$ \frac{400\text{ m/s}}{30\text{ kHz}} \approx 13.3\text{ mm} \sim 6d $$
基本可以使用长波近似.
这种速度和飞行时间速度(T.O.F. Velocity) 的比较:
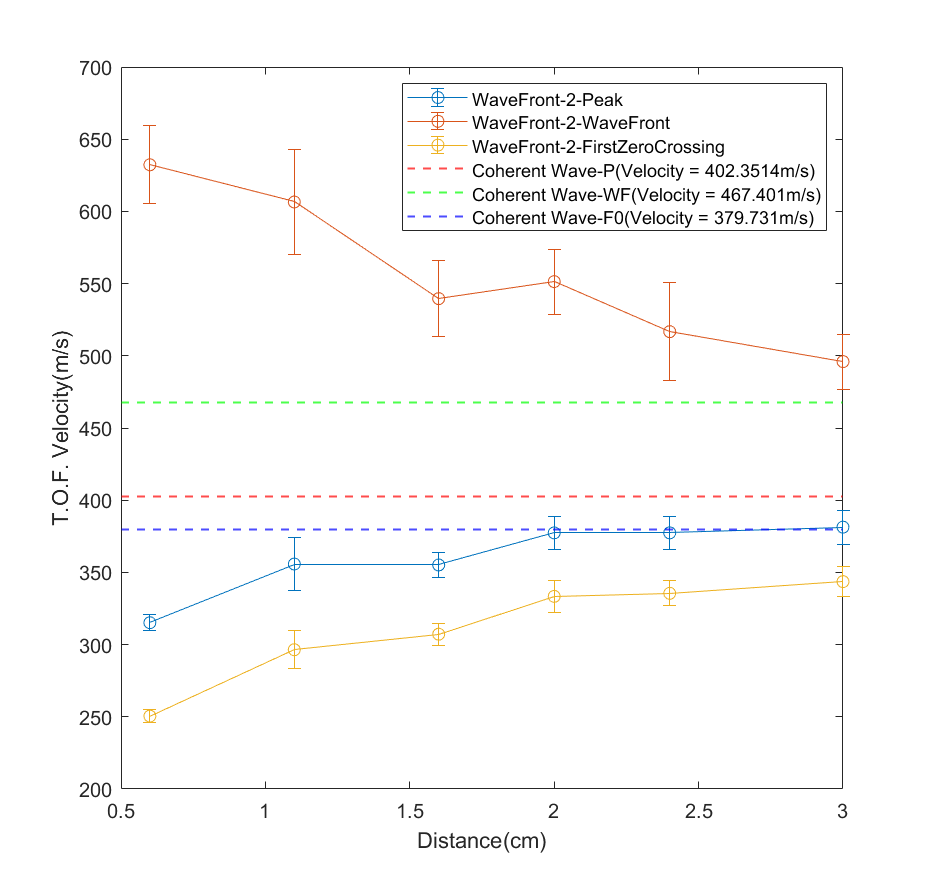
可见在测量距离大于一定情况下可以使用飞行时间法进行近似
模仿绘制声脉冲展宽的图像, 以及学习处理其归一化
注意这些声波重叠处理的时候, 归一处理的类型不同: 同一距离/厚度, 不同应力/压强(这里为了测相速度在两个距离 $x_{1}$ 和 $x_{2}$ 都测了, 但是施加的应力是相同的)
同一距离/厚度, 不同应力/压强
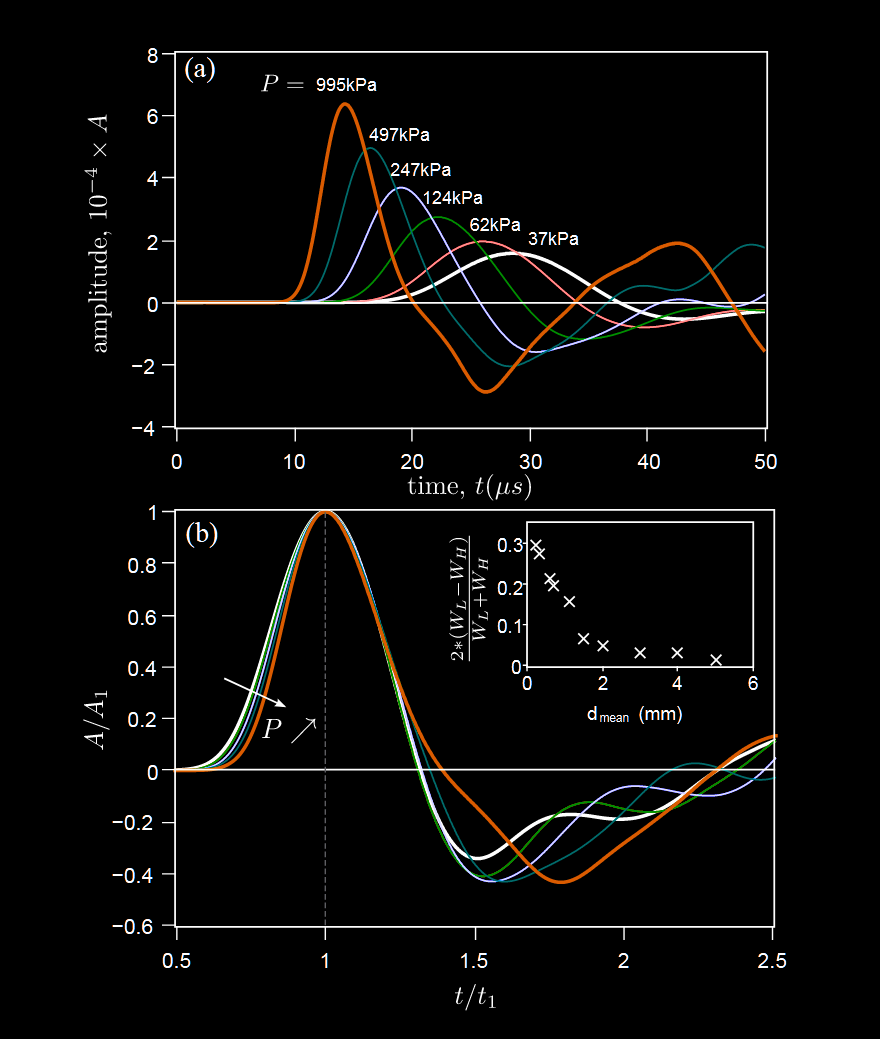
模仿的 Rescale 图像
- 时间和振幅均归一化
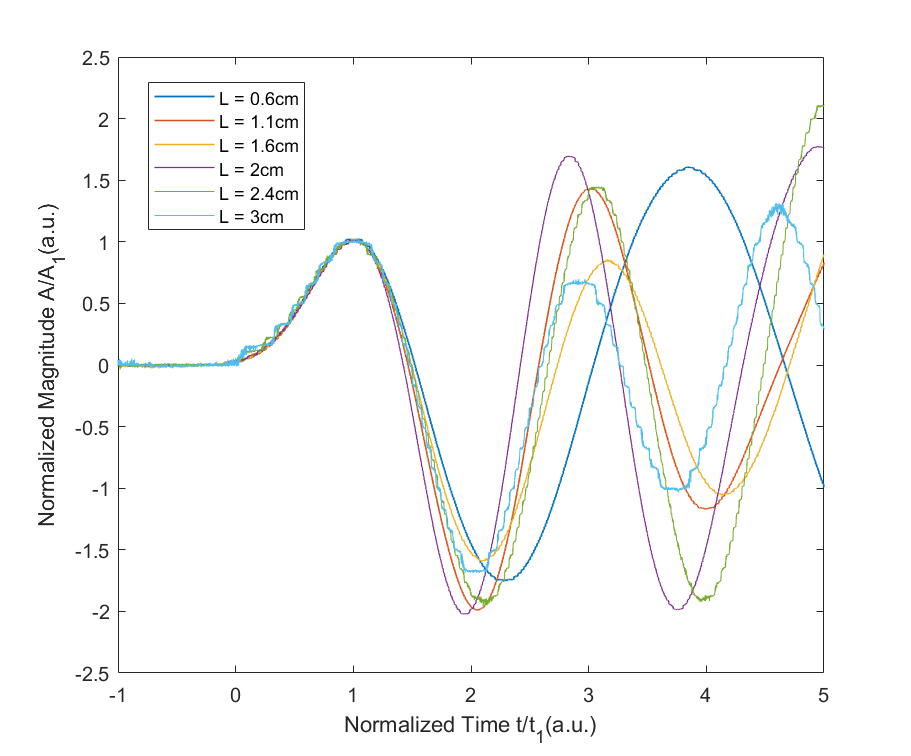
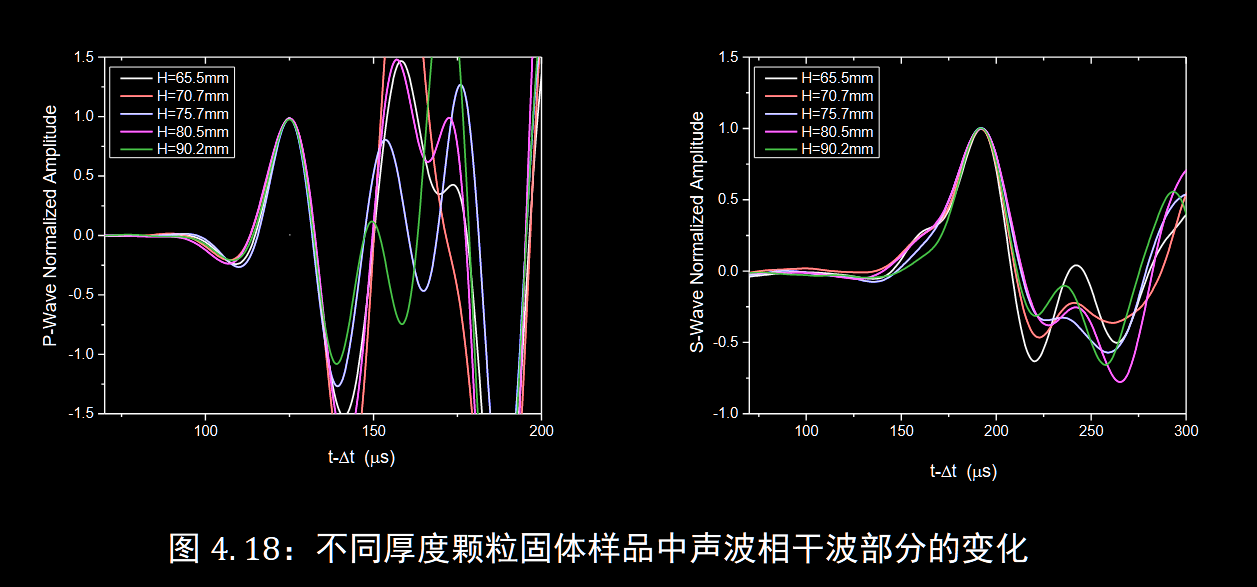
- 时间对齐于峰, 振幅归一化
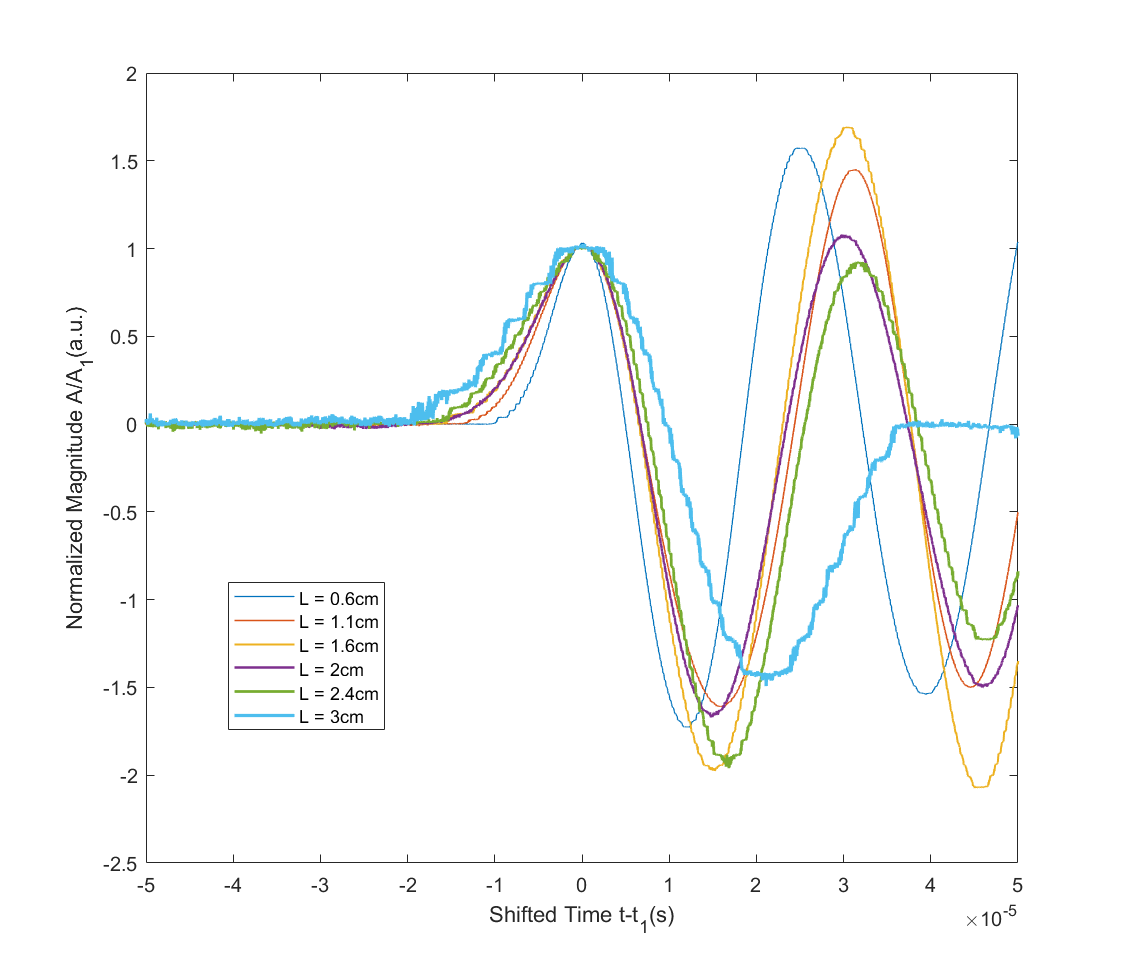
使用归一化宽度来描述在逐渐变厚的介质中的扩散行为
$$ W\sim C_{W}\left(\frac{L}{d}\right)^{-\frac{1}{2}} $$
进行的模仿实验表明出的指数非常接近($-0.47493\approx -0.5$)

需要写出一个适用于示波器的响应函数修正. 示波器的采样频率可以达到很高($\gg 2\text{ MHz}$), 按照 fft 得到的频域来一个一个试响应振幅显然是不现实的.
有一点是可以明确的: 关心的频域一般都是在 $[0,1000]\text{ kHz}$. 有一定的原因是之前的采集频率是 $2\text{ MHz}$, 但是也要根据实际的探头性能来, 目前几乎没有什么探头能够在高于 1000 kHz 的频域还能有较好的响应的.
L = []? M = [1,2,3,4,5,6,7,8,9] ensemble_size = 7
有关 TekScope 的使用小技巧
将网线连接示波器和电脑之后, 启动 TekScope, 然后再开机示波器, 此时示波器会根据 DHCP 自动分配 ip 地址, 将其填入 Host Address 即可秒连.
有关示波器和信号放大器的使用小技巧
制备颗粒堆积系综的时候, 由于使用的平均采样, 示波器 CH1 的源信号有时候会迅速衰弱. 此时调整一下信号放大器的 Gain 值即可令其回正.
相速度测量很难准确的原因在于
$$ \Delta\varphi(\omega) = \phi(\omega) + 2N(\omega)\pi $$
显然, 这里的 $N(\omega)$ 是很有可能彼此之间毫无关系的, 我们也并不能通过简单的加减 $2\pi$ 重置区间来得到正确的数值. 上面的文章中介绍了一种基于互相关方法粗略估计声速的方法. 关键词是 “连续小波变换”
对于信号 $f$, 其连续小波变换(Continous Wavelet Transform, CWT)为
$$ WT_f(a,b) = \langle f,\psi_{a,b}\rangle = \frac{1}{\sqrt{a}}\int_{R}f(t)\psi\left(\frac{t-b}{a}\right)\mathrm{d}t $$
其中 $a$ 反映了小波基的伸展或者压缩, 即尺度因子; $b$ 反映了小波基的平移, 被称为平移因子.
有关系
$$ a \cdot f = f_s \cdot f_c $$
其中 $f$ 是小波频率, $f_s$ 是信号的采样频率, $f_c$ 是小波的中心频率.
间隔 $\Delta x$ 的两个探头记录到信号 $f_{A}$ 和 $f_{B}$, 分别作 CWT 得到小波系数图, 在同一 $a$ 下分别求小波系数极值点出现的时间 $t_{A}$ 和 $t_{B}$, 即可求得相速度
$$ v_{\varphi} = \frac{\Delta x}{t_{B} - t_{A}} $$
Matlab 需要 Wavelet Toolbox 的支持.
理解归一化宽度 $W = (t_{1} - t_{0}) / t_{1}$ 的物理含义.
傅里叶变换的两个特性
$$ g(t) = f(t - t_{1}) \Rightarrow \widetilde{g}(\omega) = e^{i\omega t_{1}}\widetilde{f}(\omega) $$
$$ g(t) = f(at) \Rightarrow \widetilde{g}(\omega) = \frac{1}{|a|}\widetilde{f}\left(\frac{\omega}{a}\right) $$
$$ \begin{aligned} a(x,t) &= \frac{1}{2\pi}\int_{-\infty}^{+\infty}\widetilde{a}(\omega)e^{-i\omega t}\mathrm{d}\omega = \frac{1}{2\pi}\int_{-\infty}^{+\infty}A(\omega)e^{ik(\omega)x}e^{-i\omega t}\mathrm{d}\omega\\ &= \frac{1}{2\pi}\int_{-\infty}^{+\infty}A(\omega)e^{i[k^{\prime}(\omega) + ik^{\prime\prime}(\omega)]x}e^{-i\omega t}\mathrm{d}\omega \end{aligned} $$
对于类 Dirac 的脉冲波, 有 $A(\omega) = \delta(\omega-\omega_{0})$
- 一维质量球链($k^{\prime\prime} = 0$)
对于一维质量弹簧链, 我们已经知道色散关系
$$ \omega^{2} = \frac{4K_{s}}{M}\sin^{2}{\frac{ka}{2}} $$
使用长波极限得到波速度
$$ \omega^{2} = \frac{K_{s}}{M}k^{2}a^{2} \Rightarrow V = \frac{K_{s}}{M}a $$
具体到一维质量球, 即有 $a = 2R$, 从而得到原文中的色散关系式
$$ k = \frac{1}{R}\sin^{-1}\left(\frac{\omega R}{V}\right) $$
其中已经知道 $\arcsin{x}$ 的麦克劳林级数
$$ \sin^{-1}{x} = x + \frac{1}{2}\frac{x^{3}}{3} + \frac{1\cdot 3}{2\cdot 4}\frac{x^{5}}{5} + \cdots $$
采取长波极限 $V\rightarrow \infty$
$$ k = \frac{\omega}{V} + \frac{1}{6}\left(\frac{\omega}{V}\right)^{3}R^2 $$
所以波数项 $\text{exp}(ikx)$:
$$ \text{exp }i\left[\frac{\omega}{V}x + \frac{1}{6}\left(\frac{\omega}{V}\right)^{3}R^{2}x\right] $$
使用 $t_{1} = \frac{x}{V}$ 和 $\omega_{1} = \left(\frac{2V^3}{R^{2}x}\right)^{\frac{1}{3}}$ 简化表达式:
$$ e^{i\omega t_{1}}e^{i\left[\frac{1}{3}\left(\frac{\omega}{\omega_{1}}\right)^{3}\right]} $$
第一项可以利用傅里叶变换的时间平移性质处理. 第二项对应于 Airy 函数傅里叶变换.
$$ \mathcal{F}(\text{Ai})(\omega) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}\text{Ai}(t)e^{- i\omega t}\mathrm{d}t = e^{i\frac{1}{3}(\omega)^{3}} $$
只是使用了 $\omega_{1}$ 进行了 Rescale 操作.
所以信号
$$ a(x,t) = \omega_{1}\text{Ai}[\omega_{1}(t_{1} - t)] = \omega_{1}\text{Ai}\left[\omega_{1} t_{1}\frac{t_{1} - t}{t_{1}}\right] $$
而 $(t_{1} - t_{0})w_{1}\approx \frac{\pi}{2}$
$$ W = \frac{t_{1} - t_{0}}{t_{1}} \sim \frac{1}{\omega_{1}t_{1}} = \left(\frac{R^{2}}{2x^{2}}\right)^{\frac{1}{3}}\propto x^{-\frac{2}{3}} $$
取 $x = L$ 即得到我们熟悉的结论. 显然 $-\frac{2}{3}$ 离 $-\frac{1}{2}$ 还是有一定的差距的, 这是因为没有考虑 $k^{\prime\prime}(\omega)$ 导致的.
- 频域上的衰减 $\alpha(\omega)$
是不是可以使用求相速度的方法, 能量/功率耗散图来求解这个问题?
存在衰减
$$ \alpha = k^{\prime\prime}(\omega) = \left[\sigma_{K}^{2}L_{c}^{n-1}\right]\left(\frac{\omega}{V}\right)^{n} $$
时域信号的傅里叶变换为
$$ \widetilde{a}(\omega) = e^{ik(\omega)x} = e^{ik^{\prime }x}e^{-k^{\prime\prime }x} = e^{i\omega t_{1}}e^{-\left(\frac{\omega}{\omega_{1}}\right)^{n}} $$
其中
$$ t_{1} = \frac{x}{V},\quad \omega_{1} = \left(\frac{V^{n}}{\sigma_{K}^{2}L_{c}^{n-1}x}\right)^{\frac{1}{n}} $$
令 $s(t)$ 是 $\text{exp }(-\omega^{n})$ 的逆傅里叶变换. 则时间信号写作
$$ a(x,t) = \omega_{1}s[\omega_{1}(t-t_{1})] $$
所以
$$ W\sim\frac{1}{\omega_{1}t_{1}} = (\sigma_{K})^{\frac{2}{n}}\left(\frac{L_{c}}{x}\right)^{\frac{n-1}{n}} $$
在一维随机分层介质中, $n=2$; 代入 $x = L$ 即有
$$ W\propto L^{-\frac{1}{2}} $$
弹性模量: $K$, 密度: $\rho$.
在远距离传播时, 相干脉冲的波形趋向于高斯信号:
$$ a(L,t) = \frac{1}{\sqrt{2\pi\omega_{L}^{2}}}\text{exp}\left[-\frac{1}{2\omega_{L}^{2}}\left(t-\frac{L}{\bar{V}}\right)^{2}\right]\\ \bar{V} = \sqrt{\frac{\bar{K}}{\bar{\rho}}}\\ \omega_{L} = \sqrt{\frac{\gamma L}{2\bar{V}^{2}}}\\ \gamma = \int_{0}^{\infty}\langle\nu_{K}(0)\nu_{K}(x)\rangle\mathrm{d}x = \sigma_{K}^{2}L_{c}\\ \nu_{K} = \frac{\Delta K^{-1}}{\bar{K}^{-1}} $$
$\sigma_{K}^{2}$: 方差; $L_{c}$: 关联长度.
所以归一化宽度 $W$:
$$ W\sim \frac{\omega_{L}}{L/\bar{V}}\propto \left(\frac{\sigma_{K}^{2}L_{c}}{L}\right)^{\frac{1}{2}} $$
现在我们系统求一下衰减 $\alpha(\omega)$.
$$ \begin{aligned} \mathcal{F}[a(L,t)] &= \int_{-\infty}^{+\infty}a(L,t)e^{-i\omega t}\mathrm{d}t \\ &= \frac{1}{\sqrt{2\pi\omega_{L}^{2}}}\int_{-\infty}^{+\infty}\text{exp}\left[-\frac{1}{2\omega_{L}^{2}}\left(t-\frac{L}{\bar{V}}\right)^{2}\right]e^{-i\omega t}\mathrm{d}t \end{aligned} $$
设 $u = t - \frac{L}{\bar{V}}$, 即有 $\mathrm{d}u = \mathrm{d}t$, 代入有
$$ \mathcal{F}[a(L,t)] = \frac{1}{\sqrt{2\pi\omega_{L}^{2}}}\int_{-\infty}^{+\infty}e^{-\frac{u^{2}}{2\omega_{L}^{2}}}e^{-i\omega(u + \frac{L}{\bar{V}})}\mathrm{d}u $$
已知高斯积分公式为
$$ \int_{-\infty}^{+\infty}e^{-au^{2} + bu}\mathrm{d}u = \sqrt{\frac{\pi}{a}}e^{\frac{b^{2}}{4a}} $$
所以解得上积分式为
$$ \mathcal{F}[a(L,t)] = e^{-i\omega\frac{L}{\bar{V}}}e^{-\frac{1}{2}\omega^{2}\omega_{L}^{2}} $$
代入
$$ \omega_{L} = \sqrt{\frac{\gamma L}{2\bar{V}^{2}}} $$
即有
$$ \mathcal{F}[a(L,t)] = e^{-i\omega\frac{L}{\bar{V}}}e^{-\frac{\gamma \omega^{2}}{4\bar{V}^{2}}L} = e^{-i\omega\frac{L}{\bar{V}}}e^{-\alpha(\omega)L} $$
所以解得
$$ \alpha(\omega) = \gamma\left(\frac{\omega}{2\bar{V}}\right)^{2} $$
这符合我们在一般声学方法中推导出的 $\alpha\sim\omega^{2}$ 的规律.
- 更一般的情形(3D, $n$)
$$ \alpha\sim\sigma_{K}^{2}L_{c}^{n-1}k^{n}\sim\omega^{n} $$
频散能量图公式推导.
$$ \Gamma_{i,j}^{t}(\tau) = \int_{-\infty}^{+\infty}S_{i}(t)S_{j}(t+\tau)\mathrm{d}t $$
$$ \begin{aligned} \mathcal{F}[\Gamma_{i,j}^{t}(\tau)] &= \int_{-\infty}^{+\infty}e^{-i\omega\tau}\int_{-\infty}^{+\infty}S_{i}(t)S_{j}(t+\tau)\mathrm{d}t\mathrm{d}\tau\\ &= \int_{-\infty}^{+\infty}S_{i}(t)\int_{-\infty}^{+\infty}S_{j}(\tau+t)e^{-i\omega\tau}\mathrm{d}\tau\mathrm{d}t\\ &\overset{u = \tau + t}{=} \int_{-\infty}^{+\infty}S_{i}(t)\int_{-\infty}^{+\infty}S_{j}(u)e^{-i\omega(u-t)}\mathrm{d}u\mathrm{d}t\\ &= \int_{-\infty}^{+\infty}S_{i}(t)e^{i\omega t}\int_{-\infty}^{+\infty}S_{j}(u)e^{-i\omega u}\mathrm{d}u\mathrm{d}t\\ &=\mathcal{F}[S_{i}(t)]^{\star}\mathcal{F}[S_{j}(t+\tau)] \end{aligned} $$
傅里叶变换的平移性质:
$$ \mathcal{F}[S_{j}(t+\tau)] = e^{i\omega\tau}\mathcal{F}[S_{j}(t)] $$
所以有
$$ \mathcal{F}[\Gamma_{i,j}^{t}(\tau)] = \mathcal{F}[S_{i}(t)]^{\star}e^{i\omega\tau}\mathcal{F}[S_{j}(t)] = \mathcal{F}[S_{i}(t)]^{\star}\mathcal{F}[S_{j}(t)]e^{i\omega t} $$
或者
$$ \mathcal{F}[\Gamma_{i,j}^{t}(\tau)] = S_{i}(\omega)^{\star}S_{j}(\omega)e^{i\omega t} $$
具体在编程上, 就是取 $\delta(\omega_{n})$ 与 $\mathcal{F}[\Gamma_{i,j}^{t}(\tau)]$ 相乘, 然后进行逆傅里叶变换得到时域分布
$$ \mathcal{F}^{-1}\left\{\delta(\omega_{n})\mathcal{F}[\Gamma_{i,j}^{t}(\tau)]\right\} = \mathcal{F}^{-1}\left\{S_{i}(\omega_{n})^{\star}S_{j}(\omega_{n})e^{i\omega_{n} t}\delta(\omega_{n})\right\} $$
我们已经知道, 频域上的一个 $\delta(\omega)$ 函数, 对应于时域上的三角函数:
$$ \begin{aligned} \mathcal{F}^{-1}\left\{\delta(\omega_{n})\mathcal{F}[\Gamma_{i,j}^{t}(\tau)]\right\} &= \int_{-\infty}^{+\infty}S_{i}(\omega_{n})^{\star}S_{j}(\omega_{n})e^{i\omega_{n} t}\delta(\omega_{n})e^{i\omega\tau}\mathrm{d}\omega\\ &= S_{i}(\omega_{n})^{\star}S_{j}(\omega_{n})e^{i\omega_{n} (t+\tau)} \end{aligned} $$
这表明当
$$ \omega_{n}(\tau+t) = 2N\pi\Rightarrow \tau = \frac{2N\pi}{\omega_{n}} - t $$
时, 信号 $S_{j}(t)$ 角频率为 $\omega_{n}$ 的分量通过平移时间 $\tau$, 可以与 $S_{i}(t)$ 角频率为 $\omega_{n}$ 的分量完全重合(在功率谱上表现为 $\Gamma_{i,j}=1$), 也就是说相速度即为
$$ V_{\varphi}(\omega_{n}) = \frac{\Delta x}{\tau(N)} $$
4 月
04.08
很不容易借到了 Nonlinear Acoustics 教科书, 是 1997 年发行的, 能够在今天再看到着实不易. 很巧的是, 看到了前一位借书的同学是来自密院的郝家兴同学, 并且里面还附带了有关复印备注信息的纸条, 而且借书就在 4 月 5 日, 没有过多久.
既然在网上都没有找到什么这本书的扫描版, 我想我也应该去复制一份扫描存储, 在 DOI 高度发达的今天竟然还有书籍没有电子版, 实在是不能让人忍受的行为.
04.15
成功报名游泳培训班, 这下不用寄人篱下了, 可以安然度过本科最后的时光.
这次组会没有上去讲, 因为上一周因为杂七杂八的事情也没怎么做实验, 这周要把上周的进度补回来.
- 相速度测量.
细节要求: (1) $\delta f = f / \text{sample_length}$ 需要足够小; (2) 需要尽可能包含完整的响应信号; (3) 可以留出一定的延迟时间方便后续更高的信号处理需求. (4) 搞懂 Sound Pulse Brodening in Granular Media 里面的随机分层理论.
$\Delta f = 1\text{G}/5\text{M} = 200\text{ Hz}$
- 扩散模型
(1) 搞懂理论解是怎么做出来的, 并且在数值上将其拟合出来; (2) 控制厚度和应力大小, 观察平均自由程和扩散系数随之变化的情况;
-
颗粒介质的非线性 (1) 搞懂各个谐波的理论解是怎么导出的; (2) 基波和谐波衰减的测定. 需要 L = 1, 2, 3, 4cm 处的信号, 修正, 极窄带通滤波得到基波和谐波分量, 在距离上拟合得到衰减系数. 多个材料的测定(可能需要用到约化长度). (能不能做出 $\sim \omega^{1}$, $\sim\omega^{2}$, $\sim\omega^{4}$?) (3) 逐渐增加 $\Delta U$, 观察谐波分量与 $U_{\text{in}}$ 的关系. 可以双通道从而节约测定源振幅的时间.
-
学习有关 EMT 的仿射变换的内容, 学懂之后写到毕业论文里面.
零碎的想法
怎么使用一个声学探头, 以目前的信号发生器来实现混频($f_{1}\leq f_{2}$)?
基波和谐波的衰减测定方法: 需要用到多距离拟合
$\alpha_{3f}\neq \alpha_{3*f}$
紧锣密鼓地水论文。去除了一下模板里面关于用法部分的水分,发现虽然从昨天到今天也写了一部分,但是字数只有 4890/5078,这显然是令人沮丧的,准备继续细化一下论文内容。
04.18
你麻痹不是才期中吗,我怎么感觉我要死了。
感觉诸事不顺…买的插线板今天终于到货了,但是发现之前买的地面走线盒大小又不合适了,需要现买,到货又需要一段时间,实验无法进行。我在想要不然直接通电先把数据拿到得了
毕业论文。看规范是一共要写到两万字,现在最多也就才写到四分之一。
NI 多通道采集卡。今天和经销商聊了一下并且带到老师那里去简单交流了一下,确认了大致的需求。虽然财务应该还是大师姐来管,但是有关力学传感器和一部分仪器的研判估计还是少不了我的份。
游泳。傻逼游泳馆只接受校园卡换手带,极限转点找宣嘉乐借了卡,但是明天晚上有软凝聚态的课也补不了进度。麻。
b 站一位大佬过了地灵殿 LNN,可喜可贺。我的 lnb 依旧搁浅中…
04.22
为了测衰减做出来的效果并不好, 可能的原因:
- 探头响应太低了;
- 施加应力太小. 目前是 $9\text{ kPa}$. 继续加金属块.
方案一
在低频域范围, 用小 $\delta f$, G150 细测一遍钢珠衰减.
方案二
用 W800 测.
除此以外, 还有改变振幅测可逆性的实验, 注意信号放大器最大能放大到 25 V, 这一点还需要注意.
- 测量不同初始振幅, 各 Gain 对应的振幅值.
$$ \text{dB} = 10\lg{\frac{V}{V_{0}}} $$
$$ 2\text{dB} = 10\lg{\frac{V_{2}}{V_{0}}} - 10\lg{\frac{V_{1}}{V_{0}}} = 10\lg{\frac{V_{2}}{V_{1}}}\Rightarrow \lg\frac{V_{2}}{V_{1}} = 0.2\Rightarrow V_{2} = 10^{0.2}V_{1} $$
所以 Gain dB 对应于
$$ V_{n} = V_{0} 10^{\text{Gain}/10} $$
最大振幅为 25V, 若要对应于 20dB Gain, 则
$$ 25 = V_{0} 10^2 \Rightarrow V_{0} = 0.25\text{V} $$
若初始振幅为 $10\text{Vpp}$, 则对应的 Gain 为
$$ 25 = 10^{\text{Gain}/ 10}\Rightarrow \text{Gain}\approx 13.97 $$
实测下来 Gain 数还会比这个更少, 所以还是需要具体打表确认.
- 源振幅与颗粒结构之间的关系.
这次要彻底模仿 Jia 的振幅时域 protocol, 从而更好地复现结果.
- 相速度测量.
想办法废物利用一下 G150 的数据. 浪费好好的周末时间, 还是多少出点数据吧.
- 扩散模型.
2024.04.23
通过 $\Delta V = 1\text{ Vpp}$, $\Delta\text{Gain}=2\text{ dB}$ 打表测了振幅. 可能需要写一个小程序输出一下从小到大顺序的源振幅的 $(V_{\text{AFG}},\text{Gain})$ 组合.
我想模仿的图像
-
通过绝对 $t=0$ 叠绘的声波图像.
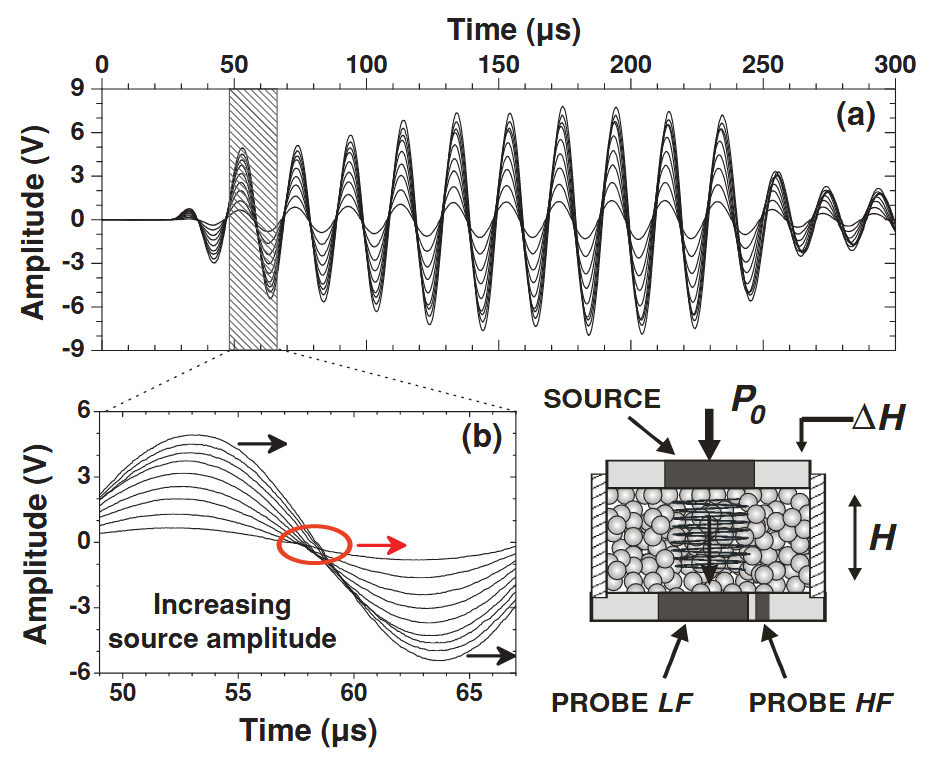
-
声压 Protocol, 相似性参数, 声速波动.
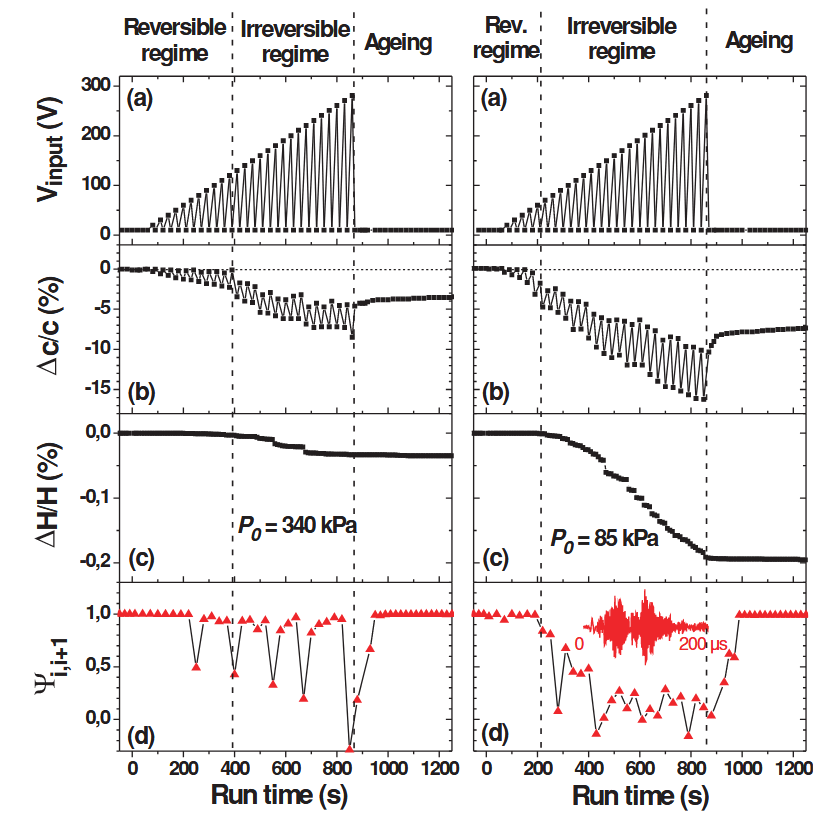
“严谨设计” 的实验做出来的效果反而不如之前的好, 有点幽默了.
$$ v = f\lambda\Rightarrow \lambda_{\text{eff}} = \frac{V_{\text{tof}}}{f_{c}} = \frac{300\text{ m/s}}{30\text{kHz}} = 10\text{ mm} \approx 3d $$
共振峰可能不止 30 khz 一个. 具体实验的时候可以大概扫一下. 31.3
成功地把 kickstart 部署到电脑上了. 可以自由地控制信号发生器.
04.25
重新做一下 irreversible 的实验。
再用类似的protocol做一遍, 效果还不好就算了.
$f_g = 47\times 10^3\text{ Hz}, f_s = 31.2\text{MHz}$
实验流程:
- 制备玻璃珠的随机密堆积。
- 粗略扫频,寻找共振峰。
- kickstart 连接示波器和发生器。 (1)调整发生器为 10-Cycle 正弦脉冲波,幅值初始为 2.0 Vpp(间隔为 0.5 或者 0.25)。 (2)调整示波器设置:双通道,采样长度200k,平均采集128,探头衰减x1.
颗粒介质对 protocol, 即制备历史具有记忆性. 1-2-1-3-1-4 和1-2-3-4 是完全不同的激励方式. 两者对于相空间探索的方式完全不同, 造成谐波分析对于前者而言很难成功.
后续做一个连续激励的, 即复现简陋装置的实验.
f = 47k
| 记录序号 | 源振幅(V) | 信号类型 |
|---|---|---|
| 1 | 2.0 | probing |
| 2 | 2.0 | probing |
| 3 | 2.0 | probing |
| 4 | 2.0 | probing |
| 5 | 2.0 | probing |
| 6 | 2.0 | probing |
| 7 | 2.0 | probing |
| 8 | 2.0 | probing |
| 9 | 2.0 | probing |
| 10 | 2.0 | probing |
| 11 | 2.0 | pumping |
| 12 | 2.0 | probing |
| 13 | 2.5 | pumping |
| 14 | 2.0 | probing |
| 15 | 3.0 | pumping |
| 16 | 2.0 | probing |
| 17 | 3.5 | pumping |
| 18 | 2.0 | probing |
| 19 | 4.0 | pumping |
| 20 | 2.0 | probing |
| 21 | 4.5 | pumping |
| 22 | 2.0 | probing |
| 23 | 5.0 | pumping |
| 24 | 2.0 | probing |
| 25 | 5.5 | pumping |
| 26 | 2.0 | probing |
| 27 | 6.0 | pumping |
| 28 | 2.0 | probing |
| 29 | 6.5 | pumping |
| 30 | 2.0 | probing |
| 31 | 7.0 | pumping |
| 32 | 2.0 | probing |
| 33 | 7.5 | pumping |
| 34 | 2.0 | probing |
| 35 | 8.0 | pumping |
| 36 | 2.0 | probing |
| 37 | 8.5 | pumping |
| 38 | 2.0 | probing |
| 39 | 9.0 | pumping |
| 40 | 2.0 | probing |
| 41 | 9.5 | pumping |
| 42 | 2.0 | probing |
| 43 | 10. | pumping |
| 44 | 2.0 | probing |
| 45 | 2.0 | probing |
| 46 | 2.0 | probing |
| 47 | 2.0 | probing |
| 48 | 2.0 | probing |
| 49 | 2.0 | probing |
| .. | 2.0 | probing |
| 50 | 2.0 | probing |
似乎声学并不一定是软化.
周志刚介绍平均场模型的附录内容有问题。多了一个莫名其妙的 $v_0$。在我自己的论文里重写了一遍.
声学黏度和动力学黏度(爱因斯坦关系)是不是等效的呢?
可能不能使用共振峰信号。这个信号对于颗粒介质的诱导效果最大。
再做一组连续的 protocol, 要是还是没效果那我就真没辙了, 用简陋实验的数据写论文算了.
9 kpa, 32 khz, 512 次平均采集, 5-循环正弦波列, 触发间隔 20ms.
循环数都是越大越好吗?
先记 10 个 1VPP 的点, 再开始 1-10, delta = 0.25 的点, 最后再做一点弛豫/aging 的点.
不知道这个波包分离,观察到的是回波(echo)还是压缩波与剪切波的分离. 作为压缩波的探头, 是否能够探测到剪切波的存在? 这个现象似乎还是因为减少了循环数才观察到的.
| 记录序号 | 源振幅(V) | 信号类型 |
|---|---|---|
| 1 | 1.00 | probing |
| 2 | 1.00 | probing |
| 3 | 1.00 | probing |
| 4 | 1.00 | probing |
| 5 | 1.00 | probing |
| 6 | 1.00 | probing |
| 7 | 1.00 | probing |
| 8 | 1.00 | probing |
| 9 | 1.00 | probing |
| 10 | 1.00 | probing |
| 11 | 1.00 | pumping |
| 12 | 1.25 | pumping |
| 13 | 1.50 | pumping |
| 14 | 1.75 | pumping |
| 15 | 2.00 | pumping |
| 16 | 2.25 | pumping |
| 17 | 2.50 | pumping |
| 18 | 2.75 | pumping |
| 19 | 3.00 | pumping |
| 20 | 3.25 | pumping |
| 21 | 3.50 | pumping |
| 22 | 3.75 | pumping |
| 23 | 4.00 | pumping |
| 24 | 4.25 | pumping |
| 25 | 4.50 | pumping |
| 26 | 4.75 | pumping |
| 27 | 5.00 | pumping |
| 28 | 5.25 | pumping |
| 29 | 5.50 | pumping |
| 30 | 5.75 | pumping |
| 31 | 6.00 | pumping |
| 32 | 6.25 | pumping |
| 33 | 6.50 | pumping |
| 34 | 6.75 | pumping |
| 35 | 7.00 | pumping |
| 36 | 7.25 | pumping |
| 37 | 7.50 | pumping |
| 38 | 7.75 | pumping |
| 39 | 8.00 | pumping |
| 40 | 8.25 | pumping |
| 41 | 8.50 | pumping |
| 42 | 8.75 | pumping |
| 43 | 9.00 | pumping |
| 44 | 9.25 | pumping |
| 45 | 9.50 | pumping |
| 46 | 9.75 | pumping |
| 47 | 10.00 | pumping |
5 月
毕业论文完成得差不多了, 就剩一点结尾. 喜提新课题, 完全没有接触过, 论文成堆地要去读. 但是我的作业和论文还有不少没做, 还有傻逼游泳测试.


