指导老师: 张杰, 远晓辉

助教: 李璟隆

研究背景

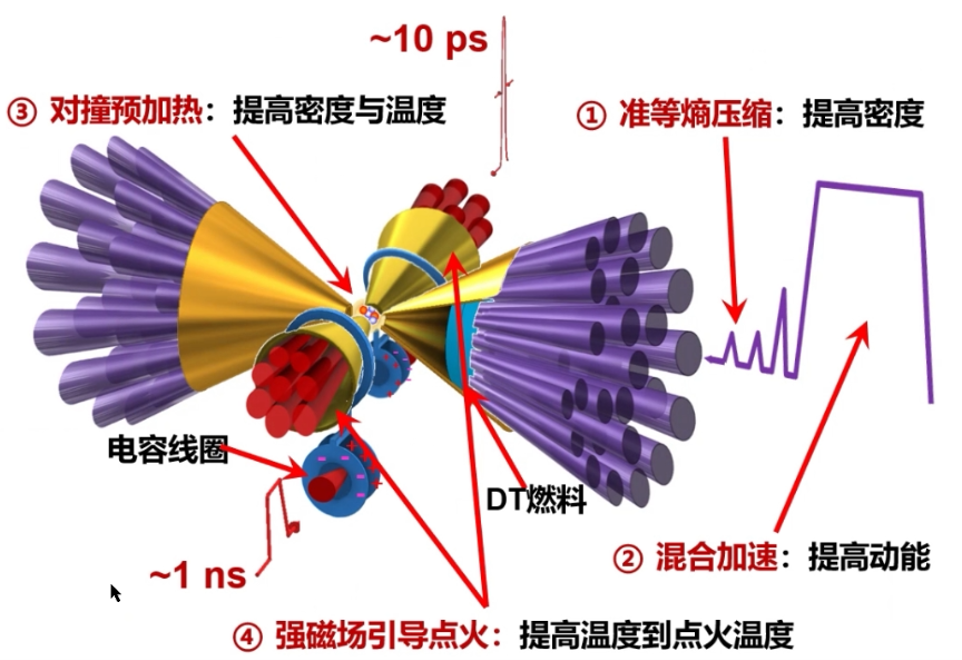
传统的中心点火方案存在两个问题:

1. 同时压缩和加热带来的不可控性;
2. 加热效率较低.

所以设计了图示的有四个步骤组成的 DCI 方案, 即

1. 准等熵压缩 $\rightarrow$ 提高密度;
2. 混合加速 $\rightarrow$ 提高动能;
3. 对撞预加热 $\rightarrow$ 提高密度和温度;
4. 强磁场引导点火 $\rightarrow$ 提高温度到点火温度;

其中我们研究的就是第三步.

快电子加热前后, 等离子体会向外发射出光谱和各种粒子. 对这些光谱和粒子的性质进行研究, 有助于获取等离子体在快电子加热前后的参数.

为了验证对撞后的等离子体的密度、快电子点火的加热是否达到预期效果，所以我们需要对等离子体参数进行诊断。在实际诊断中，可以观察中子产额、等离子体发射光谱等现象，来分析实验中的等离子体参数。等离子体光谱中包含软 $X$ 射线，硬 $X$ 射线等波段。而我们研究的就是软 $X$ 射线波段.

研究问题

我们选择等离子体光谱中的软 $X$ 射线波段($17-40$nm)进行研究的原因:

• 验证实验中采用了 CD 和 CHCl 材料，通过平场谱仪可以采集软 $X$ 射线波段的光谱曲线;
• 作为参考的碳平面靶实验为我们提供了 C 的软 $X$ 射线波段的各处谱线波长;
• 实际情况下，由于 Cl 原子在 $17-40$nm波段的谱线复杂，而 D 原子光谱远离该区域，所以我们选择 CD 材料的光谱数据加以研究。

所以我们最后选定的研究问题为:

如何研究 DCI 中快电子加热前后的等离子体所发射光谱中的软 $X$ 射线波段以判断其参数(温度，密度)?

研究方法

数据处理

坏点矫正(DPC)

在 CCD 录制下的光谱数据中存在着坏点, 在进行分析前需要先将其修复.

1. 人工修复

   由人眼搜索坏点的具体位置, 并且使用 ImageJ 来查找其具体的坐标. 然后使用其邻域的数据来填充坏点.

   因为不同发次的 CCD 拍摄角度, 拍摄距离等参数大致相同, 因此这些坏点坐标可以重复使用.

2. 坏点修复算法 这里使用的算法是常见的利用插值来修复坏点的算法. 在我们所涉及的坏点类型中, 使用线性插值即可.

   import numpy as np
   
   def interpolate(data, dp_slope=0.5, dp_thresh=3, stencil_radius=2):
      for i in range(len(data)):
        if np.isnan(data[i]):
            j = i - 1
            while np.isnan(data[j]):
                j -= 1
            k = i + 1
            while np.isnan(data[k]):
                k += 1
            if (k - j) > stencil_radius:
                data[i] = np.nan
            else:
                slope = (data[k] - data[j]) / (k - j)
                if abs(slope) > dp_slope or abs(data[k] - data[j]) > dp_thresh:
                    data[i] = np.nan
                else:
                    data[i] = data[j] + slope * (i - j)
    return data
   
   # 示例数据
   data = np.array([1, 2, np.nan, 4, np.nan, 6, 7, np.nan, 9])
   print("原始数据: ", data)
   
   # 调整参数并修复坏点
   data = interpolate(data, dp_slope=0.3, dp_thresh=2, stencil_radius=3)
   print("修复后的数据: ", data)
   

   dp_slope: 斜率阈值。当两个相邻的数据点之间的斜率超过这个阈值时，该区域被认为是不连续的，坏点将被插值而不是被修复。

   dp_thresh: 阈值。当两个相邻的数据点之间的差异超过这个阈值时，该区域被认为是不连续的，坏点将被插值而不是被修复。

   stencil radius: 模板半径。用于计算插值值的相邻数据点的数量。模板半径越大，计算出的插值值越平滑，但计算开销也会增加。

使用算法来进行坏点修复速度很快, 但是在矫正坏点的同时容易对曲线进行高斯模糊, 从而损失部分细节信息. 要在修复坏点的同时尽可能少引入高斯模糊效果, 需要对上述参数进行更细致的调整.

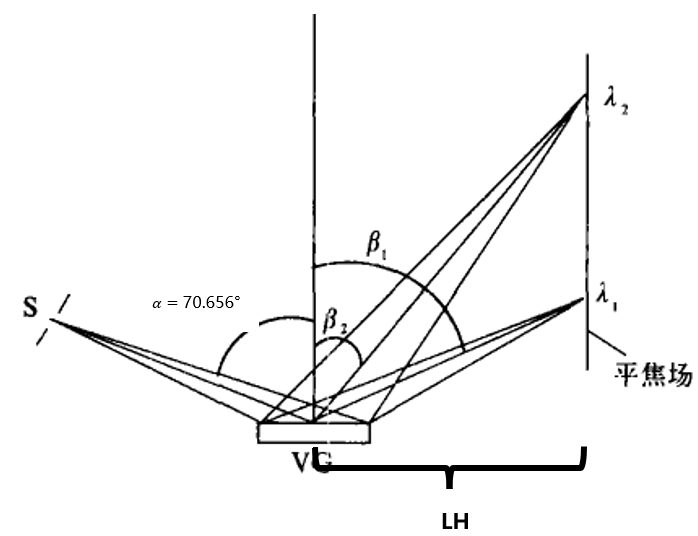
波长标定

在处理数据时, 需要建立起 CCD 像素坐标和波长之间的关系.

• Al 片的吸收边: $\lambda_{Al} = 17.1$ nm
• CCD 比例尺: k = $13.5\text{mm}/1\text{ Pixel}$
• 超环面平常光栅.

根据以上内容可以列出等式:

$$ \lambda = d_{0}(\sin{\alpha}-\sin{\arctan{\frac{LH}{x}}})\\ \lambda_{Al} = d_{0}(\sin{\alpha}-\sin{\arctan{\frac{LH}{x_{Al}}}})\\ x - x_{Al} = (Pixel_{x} - Pixel_{Al})\cdot k $$

Al 铝片具有通过吸收来对波长谱进行截断的作用, 这一点将在后面去除响应效率的部分有所展示. 所以我们可以利用图像上的吸收边作为标定像素, 从而找到参考点.

对上式进行联立化简, 即有

$$ \color{blue}{\lambda} = d_{0}\left\{\sin{\alpha}-\sin{\arctan{\left[\frac{1}{\cot{\arcsin{\left(\sin{\alpha}-\frac{\lambda_{Al}}{d_{0}}\right)}}+\left(\color{red}{Pixel_{x}}-Pixel_{Al}\right)\cdot\frac{k}{LH}}\right]}}\right\} $$

变栅距光栅具有固定的工作参数, 即 $\alpha, d_{0}, LH$

对应的工作示意图为

去除响应效率

CCD 拍摄得到的图像并不是真正的曲线, 因为光路上的各种元件不同程度地引入了响应曲线, 比如反射率\ Al 铝片吸收率\光栅反射率\CCD 响应效率函数. 所以如果要分析原始图像, 我们就需要对其进行去除.

我们测量这些曲线并且写作矩阵, 通过插值对其进行扩展. 随后使用矩阵点除依次去除曲线.

注意: 不同发次所使用的 Al 铝片的厚度不同, 因此对应的吸收曲线效果大不相同. 所以在具体的实验分析中需要对两者进行鉴别.

下图即为厚为 $1.5\mu$ m的 Al 铝片对软 $X$ 射线波段的吸收率曲线(原始数据, 未插值):

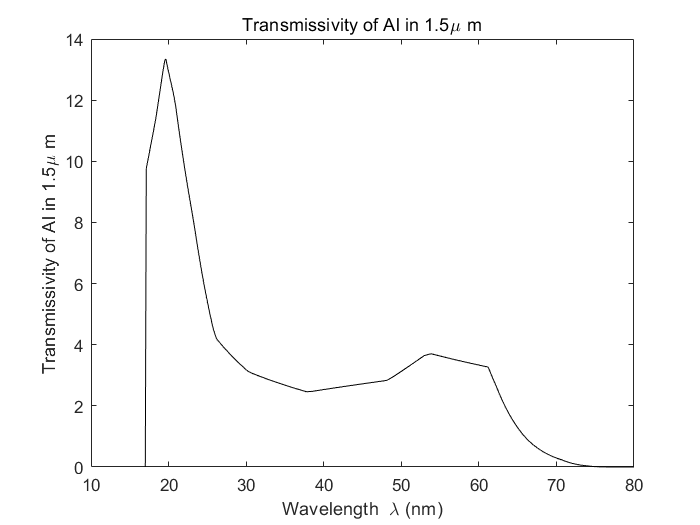
由此可以观察到明显的吸收边现象, 这也是前面所说的使用 Al 铝片帮助确定坐标的原因.

确定冕区和对撞区的 $Y$ 轴坐标

参考前面我们给出的实验室下的装置可知, 因为冕区和对撞区的温度不同, 因此对应的具体物理机制也会不同, 在 CCD 记录下的二维图像中需要数据切取, 而这个操作就需要确定具体的 $Y$ 轴坐标.

我们可以借助读取 Matlab 的工作区数据, 或者直接用 ImageJ 来选取代表性的坐标.

• 冕区: 选取连续多个 $Y$ 轴坐标和对应的采样半径, 分别进行数据平均, 挑选其中效果最好的一组;
• 对撞区: 确保采样区域在对撞区域图像的中心即可.

下面是示例性的取平均之后的数据曲线:

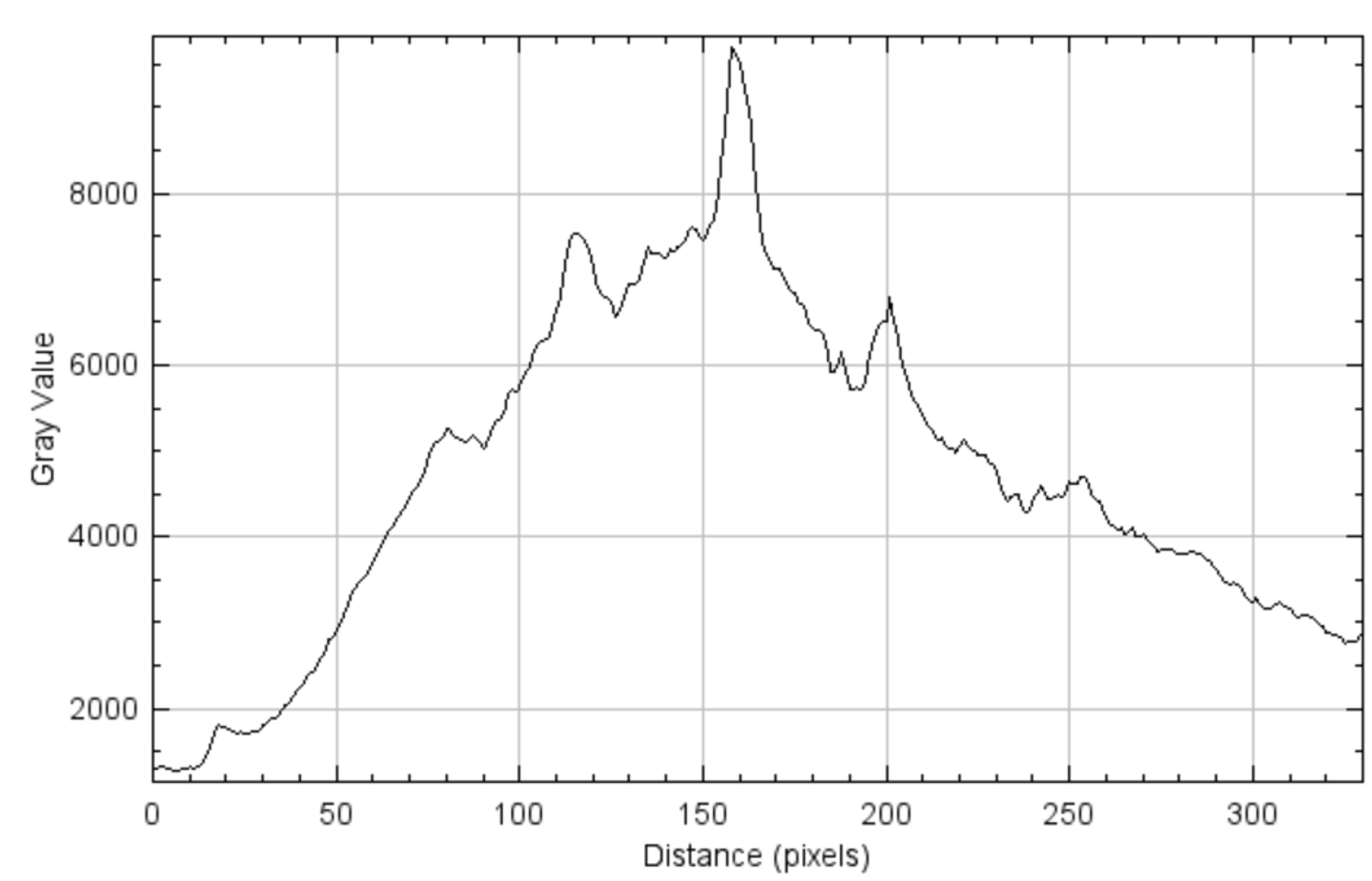
低通滤波函数处理(Low Pass Filter)

由于得到的曲线中存在高斯噪声等干扰信号, 所以在进行正式分析前需要对其进行低通滤波处理.

import numpy as np
from scipy.signal import butter, filtfilt

def butter_lowpass(cutoff, fs, order=5):
    nyq = 0.5 * fs
    normal_cutoff = cutoff / nyq
    b, a = butter(order, normal_cutoff, btype='low', analog=False)
    return b, a

def lowpass_filter(data, cutoff, fs, order=5):
    b, a = butter_lowpass(cutoff, fs, order=order)
    y = filtfilt(b, a, data)
    return y

# 生成示例数据
t = np.linspace(0, 1, 1000)
data = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t) + np.random.randn(len(t))*0.1

# 设置滤波器参数
cutoff = 15  # 截止频率
fs = 1000  # 采样率
order = 6  # 滤波器阶数

# 应用低通滤波器
filtered_data = lowpass_filter(data, cutoff, fs, order=order)

上述代码仅为示例, 实际工作中的处理是使用 Matlab 处理完成的.

和矫正坏点类似, 这样的算法处理会引入高斯模糊, 从而损失部分的细节信息, 所以在去除干扰和避免信息损失之间需要做好权衡.

输出光谱横坐标

因为在上述的操作过程中, $Pixel_{Al}$ 实际上是手动选中的, 所以可能会引入 $\lambda$ 标定的误差.

然而我们除了正式的对撞模拟实验之外, 还有碳平面参考靶产生的实验数据, 我们可以对两者的峰进行对比确认.

光谱机制

发光机制按照其曲线形状可以分为连续谱和线谱.

连续谱

连续谱中的发光机制主要有轫致辐射和复合辐射.

• 轫致辐射 电子在离子的库仑力作用下做非匀速运动, 电子在这个过程中丢失动能, 从而发出电磁辐射. $$ \color{red}{W_{B}}\propto\frac{Z^{2}e^{6}}{mc^{2}}\frac{n_{e}n_{i}}{h}\left(\frac{2k_{B}T_{e}}{\pi m}\right) $$

  $\color{red}{W_{B}}$: 布洛赫辐射的辐射能量密度; $Z$: 等离子体中的离子电荷数; $e$: 元电荷; $m$: 电子质量; $c$: 光速; $n_{e}$: 等离子体中的电子密度; $n_{i}$: 等离子体中的离子密度; $h$: 普朗克常数; $k_{B}$: 玻尔兹曼常数; $T_{e}$: 等离子体中的电子温度;

• 复合辐射 自由态电子和离子的价态空穴进行结合, 电子回到某个能级上从而发出辐射: $$ \color{lightblue}{W_{r}}\approx 2.4\frac{Z^2E_{H}}{k_{B}T_{e}}\color{red}{W_{B}} $$

  $\color{lightblue}{W_{r}}$; 布洛赫辐射的总辐射能量密度; $Z$: 等离子体中的离子电荷数; $E_{H}$: 氢原子的电离能; $k_{B}$: 玻尔兹曼常数; $T_{e}$: 等离子体中的电子温度; $\color{red}{W_{B}}$: 布洛赫辐射的辐射能量密度;

从所列出的公式可以看出, 轫致辐射对应的功率与 $Z^{2}$ 成正比, 所以我们猜测 CD 材料能引起的轫致辐射功率是相对小的; 而在低 $Z$ 数下, 复合辐射相对于轫致辐射还要更小(观察系数), 所以我们作出这样的推测: 连续谱可能在实际的谱线中并不占主导地位.

所以要对光谱进行分析, 还要再看线状谱.

线状谱

我们已经在研究问题部分介绍到, 软 $X$ 射线波段的量级大约为 $0.1$$10$nm, 所以当处理 CD 作为靶材料的数据时, 应当重点关注 C 的谱线, 也就是 $17$$40$nm.

但是在真实的实验条件下, 线谱必定会因为各种原因出现展宽(即线谱的半高全宽), 对其出现原因的研究也很有意义.

1. 自然展宽

   由不确定性原理造成的展宽: $$ \Delta E\cdot\Delta t\geq h $$

2. 多普勒展宽

   粒子热运动造成原子与仪器之间的相对运动, 从而影响到所接收的频率, 而热运动的速率分布遵从麦克斯韦统计: $$ G(x,\sigma) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^{2}}{2\sigma^{2}}} $$

3. Stark 展宽

   一种压力展宽, 辐射粒子受到周围带电粒子的含时微场的影响从而产生展宽, 这会使得激发态电子的寿命变短.

   同时, 由于能级分裂, 也会产生谱线的偏移: $$ L(x,\gamma)=\frac{\gamma}{\pi(x^{2}+\gamma^{2})} $$

在真实的实验条件下, 谱线的实际形状是由以上几种效应的卷积, 也就是高斯线型和洛伦兹线型的卷积(Voigt 线型)

数据分析

以 CD 发次的对撞实验进行分析. 观察可知, 在 C 的几个经典的离化态对应的波长处均有小峰, 这和纯碳平面参考靶给出的实验数据是吻合的. 一共是 $18.2, 22.7, 24.9, 26.7, 28.9, 31.2$ 六条谱线最为直观.

每条谱线的展宽主要受到多普勒效应

$$ \Delta\nu_{1/2} = 2\sqrt{\frac{(2\ln{2})k_{B}T}{mc^{2}}}\nu_{0}\\ \Rightarrow \Delta\lambda_{1/2}=2\sqrt{\frac{(2\ln{2})k_{B}T}{mc^{2}}}\lambda_{0} $$

和 Stark 效应

$$ \Delta\lambda_{1/2}=2.5\times 10^{-13}\alpha_{1/2}N_{e}^{2/3} $$ 的影响.

代入一些典型参数后, 验算得知多普勒展宽约为 $10^{-3}$nm, 而 Stark 展宽大致为 $0.1$~$1$nm, 多普勒线型和 Stark 效应的洛伦兹线型做卷积后的半高全宽中 Stark 效应将会占主导地位, 这和实际曲线中的情况是相符的.

而另一方面, CD 加热前后发次的谱线展宽实际上相差不大, 这是因为 Stark 下效应本身受电子数密度的影响更大, 而快电子加热过程中对于密度的影响较小, 这和实验结果相符合.

根据 Stark 效应半高全宽的经验公式, 大致估算其电子数密度量级约为 $10^{24}/\text{cm}^{3}$, 等离子体密度量级约为 $10\text{g}/\text{cm}^{3}$.

除了上述分析外还存在一些问题.

• Stark 效应带来的除了谱线的展宽, 应该还会有中心波长的偏移, 其中有些实验数据是符合的, 但是有些数据则会存在差别;
• 某些发次的实验中在并不存在碳的离化态所对应的谱线位置出现了尖峰.

以上产生的与理论预测之间的矛盾可能是

• 数据处理过程中波长的标定;
• 滤波函数的选择;
• 坏点的去除程度;
• 单次实验本身的误差

等因素导致的.

数值模拟

很遗憾的是在实践期间, 由于各种因素数值模拟的工作进行得并不成功, 但是由此学习到的科研工具的确有必要记录下来. 该部分因为内容问题未被展示在期末答辩的内容上.

FLYCHK

FLYCHK 是由 NIST 开发的半公开等离子体光谱数据库, 输入原子序数, 温度, 密度等初始信息可以获取该条件下的发射光谱.

使用时需要向维护者 Dr.Yuri Ralchenko 发送申请邮件以获取访问 ID 和密码.

FLYCHK 只会保存最近14天的运行结果, 所以确保将运行数据导出并妥善保存.

有时候访问 FLYCHK 可能会出现 404 错误, 这是网站管理人员对其进行维护导致的, 维护时间可能长达数月, 所以要做好心理准备.

因为我们的目的是要验证理论模型是否正确, 所以通过 FLYCHK 模拟计算等离子体的光谱发射\离化态分布是可行的.

PrismSPECT

PrismSPECT 是由棱镜计算科学公司开发的用于计算等离子体辐射光谱的商业软件, 通常用于模拟实验室和天体物理的物质辐射性质.

这套软件对于个人而言价格昂贵, 一般都是由实验组购买并且分发密钥进行使用. 所以在这里不进行过多介绍.

总结与展望

总结

• 成功将数据处理得到了可供分析的实际的光谱曲线;
• 理解光谱发射机制，并且能以此为根据，对实验发次的部分参数进行数量级上的预测;
• 掌握 FLYCHK 等数据库与软件的使用方法，从而通过调整参数逼近实验曲线，给出实验曲线的等离子体参数.

展望

• 目前处理的数据主要集中在 CD 上，可以对同样作为实验燃料的 CHCl 展开光谱研究，从而得出更广度的结论；
• 目前的研究手段主要集中在对碳的线谱上，可以学习更多的机制从而对连续谱方面进行半定量研究；
• 数据分析目前局限在单次的调参和模拟，在未来可以设法批量生成光谱曲线从而建设供机器学习的数据库。

参考文献

[1]刘运全,张杰,陈正林,彭晓昱.软 $X$ 射线平场光谱仪系统的优化设计[J].物理学报,2004(05):1433-1439.

[2]李璟隆.对激光聚变物理过程的软 $X$ 射线诊断研究[D].上海:华东师范大学物理与电子科学学院,2021(5).

[3] Giulietti D, Gizzi L A. $X$-ray emission from laser-produced plasmas[J]. La Rivista del Nuovo Cimento (1978-1999), 1998, 21(10): 1-93.

[4]Wu, F., Yang, X., Ma, Y., Zhang, Q., Zhang, Z., Yuan, X., . . . Zhang, J. (2022). Machine-learning guided optimization of laser pulses for direct-drive implosions. High Power Laser Science and Engineering, 10, E12. doi:10.1017/hpl.2022.4

[5]倪元龙,毛楚生,吴江,余松玉,周正良,傅思祖,顾援,王世绩.平焦场光栅光谱仪[J].强激光与粒子束,1991(02):242-248.

[6] Giulietti D, Gizzi L A. $X$-ray emission from laser-produced plasmas[J]. La Rivista del Nuovo Cimento (1978-1999), 1998, 21(10): 1-93.

[7] De Giacomo A, Hermann J. Laser-induced plasma emission: from atomic to molecular spectra[J]. Journal of Physics D: Applied Physics, 2017, 50(18): 183002.

[8] Spencer J B, Alman D A, Ruzic D N, et al. Dynamics of a laser produced plasma for soft x-ray production[C]//Emerging Lithographic Technologies IX. SPIE, 2005, 5751: 798-807.

[9]H.R. Griem. Plasma spectroscopy [M]. New York: McGraw-Hill, 1964

[10]鲁建. 稠密等离子体诊断用 $X$ 射线均匀色散弯晶谱仪研究[D]. 重庆: 重庆大学, 2015.